ريتشارد هامينج: الفصل 13. نظرية المعلومات

لقد فعلناها!

"إن الهدف من هذه الدورة هو إعدادك لمستقبلك الفني."

مرحباً هابر. تذكر المقال الرائع "أنت وعملك " (+219 ، 2588 إشارة مرجعية ، قراءة 429 ألف)؟

لذا فإن هامينج (نعم ، نعم ، رموز التحقق الذاتي والتصحيح الذاتي لهامينج ) لديها كتاب كامل مكتوب على أساس محاضراته. نحن نترجمها ، لأن الرجل يتحدث عن الأعمال.

هذا الكتاب لا يتعلق فقط بتكنولوجيا المعلومات ، إنه كتاب عن أسلوب التفكير لدى الأشخاص الرائعين بشكل لا يصدق. "هذه ليست مجرد تهمة للتفكير الإيجابي ، يصف الظروف التي تزيد من فرص القيام بعمل عظيم ".

شكرا للترجمة إلى أندريه باخوموف.

تم تطوير نظرية المعلومات بواسطة C.E. Shannon في أواخر الأربعينيات. أصرّت إدارة مختبرات Bell على تسميته "نظرية الاتصال" لأنه هذا اسم أكثر دقة. لأسباب واضحة ، فإن اسم "نظرية المعلومات" له تأثير أكبر بكثير على الجمهور ، لذلك اختار شانون ذلك ، وهذا ما نعرفه حتى يومنا هذا. يشير الاسم نفسه إلى أن النظرية تتعامل مع المعلومات ، مما يجعلها مهمة ، لأننا نتوغل بشكل أعمق في عصر المعلومات. في هذا الفصل ، سوف أتطرق إلى بعض الاستنتاجات الأساسية من هذه النظرية ، ولن أقدم دليلاً صارمًا ، بل بالأحرى بديهيًا على بعض الأحكام المنفصلة لهذه النظرية ، حتى تفهم ماهية "نظرية المعلومات" حقًا ، حيث يمكنك تطبيقها وأين لا .

بادئ ذي بدء ، ما هي "المعلومات"؟ يحدد شانون المعلومات مع عدم اليقين. اختار اللوغاريتم السلبي لاحتمال وقوع حدث ما كمقياس كمي للمعلومات التي تتلقاها عند وقوع حدث باحتمال ص. على سبيل المثال ، إذا أخبرتك أن الطقس في لوس أنجلوس ضبابي ، فإن p قريبة من 1 ، والتي بشكل عام لا تعطينا الكثير من المعلومات. ولكن إذا قلت أنها تمطر في مونتيري في يونيو ، فسيكون هناك عدم يقين في هذه الرسالة ، وسوف تحتوي على مزيد من المعلومات. لا يحتوي الحدث الموثوق على أي معلومات ، حيث أن السجل 1 = 0.

دعونا نتناول هذا بمزيد من التفصيل. يعتقد شانون أن المقياس الكمي للمعلومات يجب أن يكون وظيفة مستمرة لاحتمال الحدث ص ، ويجب أن يكون مضافة بالنسبة للأحداث المستقلة - يجب أن تكون كمية المعلومات التي يتم الحصول عليها نتيجة حدثين مستقلين مساوية لكمية المعلومات التي تم الحصول عليها نتيجة لحدث مشترك. على سبيل المثال ، عادةً ما تُعتبر نتيجة رمي النرد والعملات المعدنية أحداثًا مستقلة. دعونا نترجم ما سبق إلى لغة الرياضيات. إذا كان I (p) هو مقدار المعلومات الواردة في الحدث مع الاحتمال p ، فعندئذ بالنسبة للحدث المشترك الذي يتكون من حدثين مستقلين x مع الاحتمالية p ₁ و y مع الاحتمال p ₂ نحصل


(أحداث x و y المستقلة)

هذه هي معادلة كوشي الوظيفية ، صحيحة لكل p ₁ و p2. لحل هذه المعادلة الوظيفية ، افترض ذلك

ص ₁ = ص ₂ = ص ،

يعطي



إذا كانت p ₁ = p ² و p ₂ = p ، إذن



الخ. توسيع هذه العملية باستخدام الطريقة القياسية لأسس لجميع الأرقام المنطقية م / ن ، ما يلي صحيح



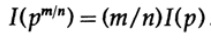
من الاستمرارية المفترضة لقياس المعلومات ، يستتبع ذلك أن الدالة اللوغاريتمية هي الحل المستمر الوحيد لمعادلة كوشي الوظيفية.

في نظرية المعلومات ، من المعتاد أن تأخذ قاعدة اللوغاريتم من 2 ، لذلك فإن الخيار الثنائي يحتوي على 1 بت بالضبط من المعلومات. لذلك ، يتم قياس المعلومات بواسطة الصيغة



دعونا نتوقف ونرى ما حدث أعلاه. بادئ ذي بدء ، لم نقدم تعريفاً لمفهوم "المعلومات" ، بل حددنا للتو صيغة لقياسها الكمي.

ثانيًا ، يعتمد هذا الإجراء على عدم اليقين ، وعلى الرغم من أنه مناسب بما فيه الكفاية للآلات - على سبيل المثال ، أنظمة الهاتف ، والإذاعة ، والتلفزيون ، وأجهزة الكمبيوتر ، وما إلى ذلك - إلا أنه لا يعكس الموقف البشري العادي تجاه المعلومات.

ثالثًا ، هذا مقياس نسبي ، يعتمد على الحالة الحالية لمعرفتك. إذا نظرت إلى دفق "الأرقام العشوائية" من منشئ الأرقام العشوائية ، فإنك تفترض أن كل رقم تالٍ غير محدد ، ولكن إذا كنت تعرف صيغة حساب "الأرقام العشوائية" ، فسيتم معرفة الرقم التالي ، وبالتالي لن يحتوي على المعلومات.

وبالتالي ، فإن التعريف الذي قدمه شانون للمعلومات في كثير من الحالات مناسب للآلات ، ولكن لا يبدو أنه يتوافق مع الفهم الإنساني للكلمة. لهذا السبب ، يجب أن تسمى "نظرية المعلومات" "نظرية الاتصال". ومع ذلك ، فات الأوان لتغيير التعريفات (بفضل اكتساب النظرية شعبيتها الأولية ، والتي لا تزال تجعل الناس يعتقدون أن هذه النظرية تتعامل مع "المعلومات") ، لذلك علينا أن نتحملها ، ولكن يجب عليك فهم بوضوح مدى البعد عن تعريف المعلومات التي قدمها شانون بعيدًا عن الحس السليم. تتعامل معلومات شانون مع شيء مختلف تمامًا ، ألا وهو عدم اليقين.

هذا ما تحتاج إلى التفكير فيه عندما تقدم أي مصطلحات. ما مدى اتساق التعريف المقترح ، على سبيل المثال ، التعريف الذي قدمه شانون ، مع فكرتك الأصلية ، وما مدى اختلافه؟ لا يوجد أي مصطلح تقريبًا يعكس بدقة رؤيتك السابقة للمفهوم ، ولكن في النهاية ، فإن المصطلحات المستخدمة هي التي تعكس معنى المفهوم ، لذا فإن إضفاء الطابع الرسمي على شيء ما من خلال تعريفات واضحة دائمًا ما يحدث بعض الضوضاء.

خذ بعين الاعتبار النظام الذي تتكون أبجديته من الرموز q مع الاحتمالات pi. في هذه الحالة ، يكون متوسط ​​كمية المعلومات في النظام (قيمته المتوقعة) هو:



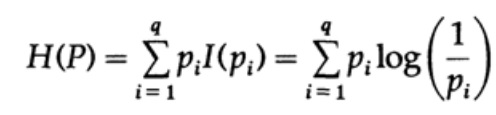
وهذا ما يسمى إنتروبيا نظام التوزيع الاحتمالي {pi}. نستخدم مصطلح "الانتروبيا" لأن نفس الشكل الرياضي ينشأ في الديناميكا الحرارية والميكانيكا الإحصائية. هذا هو السبب في أن مصطلح "الكون" يخلق حوله هالة من الأهمية ، والتي ، في نهاية المطاف ، لا مبرر لها. نفس الشكل الرياضي للتدوين لا يعني نفس تفسير الشخصيات!

تلعب إنتروبيا التوزيع الاحتمالي دورًا رئيسيًا في نظرية الترميز. يعد عدم المساواة في جيبس ​​لتوزيعتين احتماليتين مختلفتين pi و qi أحد النتائج المهمة لهذه النظرية. لذا علينا أن نثبت ذلك



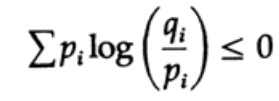
يعتمد الدليل على رسم بياني واضح ، شكل. 13.I ، مما يدل على ذلك



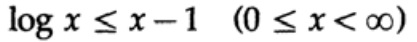
ويتم تحقيق المساواة فقط لـ x = 1. نطبق عدم المساواة على كل تلخيص للمجموع من الجانب الأيسر:



إذا كانت الأبجدية لنظام الاتصال تتكون من أحرف q ، فعندئذٍ مع الأخذ في الاعتبار احتمال إرسال كل حرف qi = 1 / q واستبدال q ، نحصل من عدم المساواة Gibbs





الشكل 13.I

هذا يشير إلى أنه إذا كان احتمال إرسال جميع الأحرف q هو نفسه ويساوي - 1 / q ، فإن الحد الأقصى للانتروبيا هو ln q ، وإلا فإن التفاوت يبقى.

في حالة رمز تم فك تشفيره بشكل فريد ، لدينا عدم المساواة في Kraft



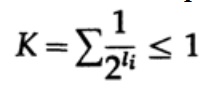
الآن إذا حددنا الاحتمالات الزائفة



أين بالطبع = 1 ، الذي ينبع من عدم المساواة في جيبس ​​،



ونطبق بعض الجبر (تذكر أن K ≤ 1 ، حتى نتمكن من حذف المصطلح اللوغاريتمي ، وربما تعزيز عدم المساواة لاحقًا) ، نحصل على



حيث L هو متوسط ​​طول الشفرة.

وبالتالي ، فإن الكون هو الحد الأدنى لأي رمز حرف بمتوسط ​​كلمة مشفرة L. هذه هي نظرية شانون لقناة دون تدخل.

الآن نحن نعتبر النظرية الرئيسية حول قيود أنظمة الاتصالات التي يتم فيها إرسال المعلومات في شكل دفق من البتات المستقلة والضوضاء. من المفترض أن احتمال الإرسال الصحيح للبتة الواحدة هو P> 1/2 ، واحتمال أن يتم عكس قيمة البت أثناء الإرسال (يحدث خطأ) هو Q = 1 - P. للراحة ، نفترض أن الأخطاء مستقلة واحتمال الخطأ هو نفسه لكل مرسلة بت - أي أن هناك "ضوضاء بيضاء" في قناة الاتصال.

الطريقة التي لدينا دفق طويل من البتات n المشفرة في رسالة واحدة هي امتداد n- الأبعاد لرمز بت واحد. سنحدد قيمة n لاحقًا. ضع في اعتبارك رسالة تتكون من n-bits كنقطة في الفضاء ذي الأبعاد n. نظرًا لأن لدينا مساحة ذات أبعاد n - ومن أجل البساطة نفترض أن كل رسالة لها نفس احتمالية حدوثها - هناك M رسائل محتملة (سيتم تحديد M أيضًا في وقت لاحق) ، وبالتالي ، فإن احتمال أي رسالة مرسلة يساوي




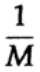
(مرسل)
الرسم البياني 13.II

بعد ذلك ، ضع في اعتبارك فكرة عرض النطاق الترددي للقناة. بدون الخوض في التفاصيل ، يتم تعريف سعة القناة على أنها أقصى قدر من المعلومات التي يمكن إرسالها بشكل موثوق عبر قناة الاتصال ، مع الأخذ في الاعتبار استخدام التشفير الأكثر كفاءة. لا يوجد جدل حول إمكانية إرسال المزيد من المعلومات عبر قناة الاتصال أكثر من قدرتها. يمكن إثبات ذلك لقناة متناظرة ثنائية (والتي نستخدمها في حالتنا). يتم تعيين سعة القناة لإرسال بت على النحو



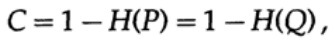
حيث ، كما كان من قبل ، P هي احتمال عدم وجود خطأ في أي بتة مرسلة. عند إرسال n بتة مستقلة ، يتم تحديد سعة القناة على أنها



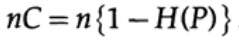
إذا كنا قريبين من عرض النطاق الترددي للقناة ، فيجب أن نرسل هذا الحجم من المعلومات تقريبًا لكل من الأحرف ai ، i = 1 ، ... ، M. نظرًا لأن احتمال حدوث كل حرف ai هو 1 / M ، نحصل على



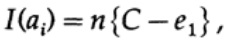
عندما نرسل أيًا من رسائل M المتساوية ، لدينا



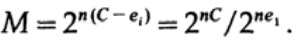
عند إرسال n بت ، نتوقع حدوث أخطاء nQ. من الناحية العملية ، بالنسبة للرسالة التي تتكون من n-bits ، سيكون لدينا أخطاء nQ تقريبًا في الرسالة المستلمة. بالنسبة إلى n ، الاختلاف النسبي (الاختلاف = عرض التوزيع)
توزيع عدد الأخطاء سيكون أضيق مع زيادة ن.

لذا ، من جانب جهاز الإرسال ، آخذ رسالة ai لإرسال ورسم كرة حوله بنصف قطر



وهو أكبر بقليل بمقدار يساوي e2 من العدد المتوقع للأخطاء Q (الشكل 13.II). إذا كانت n كبيرة بما يكفي ، فهناك احتمال صغير بشكل تعسفي لظهور نقطة الرسالة bj على جانب المستقبل ، وهو ما يتجاوز هذا المجال. سنرسم الموقف ، كما أراه من وجهة نظر المرسل: لدينا أي نصف قطر من الرسالة المرسلة ai إلى الرسالة المستلمة bj مع احتمال خطأ يساوي (أو يساوي تقريبًا) التوزيع الطبيعي ، ويصل إلى الحد الأقصى في nQ. بالنسبة لأي e2 معين ، هناك n كبيرة جدًا لدرجة أن احتمال أن تكون النقطة الناتجة bj ، التي تتجاوز المجال الخاص بي ، ستكون صغيرة كما تريد.

الآن فكر في نفس الموقف من جانبك (الشكل 13.III). على جانب جهاز الاستقبال يوجد كرة S (r) من نفس نصف القطر r حول النقطة المستقبلة bj في مساحة n-dimensional ، بحيث إذا كانت الرسالة المستلمة bj داخل المجال الخاص بي ، فإن الرسالة ai التي أرسلتها تكون داخل المجال الخاص بك.

كيف يمكن أن يحدث خطأ؟ يمكن أن يحدث خطأ في الحالات الموضحة في الجدول أدناه:



الشكل 13.III



هنا نرى أنه في المجال الذي تم إنشاؤه حول النقطة المستقبلة هناك نقطة واحدة على الأقل تتوافق مع رسالة محتملة غير مشفرة ، ثم حدث خطأ أثناء الإرسال ، حيث لا يمكنك تحديد أي من هذه الرسائل تم إرسالها. لا تحتوي الرسالة المرسلة على أخطاء إلا إذا كانت النقطة المقابلة لها في المجال ، ولا توجد نقاط أخرى محتملة في هذا الرمز موجودة في نفس المجال.

لدينا معادلة رياضية لاحتمال خطأ Re إذا تم إرسال ai



يمكننا التخلص من العامل الأول في الفصل الثاني ، مع اعتباره 1. وبالتالي نحصل على عدم المساواة



من الواضح ،



لذلك



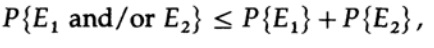
إعادة التقديم على العضو الأخير على اليمين



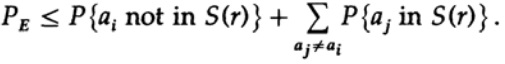
إذا تم أخذ n بشكل كبير بما فيه الكفاية ، فيمكن أن يتم أخذ الحد الأول بشكل تعسفي ، على سبيل المثال ، أقل من رقم معين د. لذلك لدينا



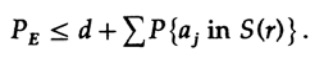
دعنا الآن نرى كيف يمكنك إنشاء رمز بديل بسيط لترميز رسائل M التي تتكون من n بت. نظرًا لعدم وجود فكرة عن كيفية إنشاء الرمز (لم يتم اختراع رموز تصحيح الخطأ بعد) ، اختار شانون الترميز العشوائي. اقلب عملة لكل من البتات n في الرسالة وكرر العملية لرسائل M. كل ما عليك فعله هو رمي عملة nM ، لذا من الممكن



قواميس الكود لها نفس احتمالية ½nM. بالطبع ، تعني العملية العشوائية لإنشاء دفتر تشفير أن هناك احتمال لتكرار ، بالإضافة إلى نقاط الرمز ، التي ستكون قريبة من بعضها البعض ، وبالتالي ، ستكون مصدرًا للأخطاء المحتملة. من الضروري إثبات أنه إذا لم يحدث هذا مع احتمال أعلى من أي مستوى خطأ صغير محدد ، فإن n المعطاة كبيرة بما يكفي.
النقطة الحاسمة هي أن شانون قام بحساب متوسط ​​جميع كتب الكود الممكنة للعثور على متوسط ​​الخطأ! سنستخدم رمز Av [.] للإشارة إلى المتوسط ​​عبر مجموعة جميع قواميس الكود العشوائية الممكنة. يعطي المتوسط ​​على الثابت د ، بالطبع ، ثابتًا ، لأن متوسط ​​كل مصطلح يتطابق مع أي مصطلح آخر في المجموع



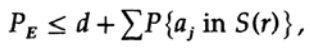
التي يمكن زيادتها (M - 1 تذهب إلى M)



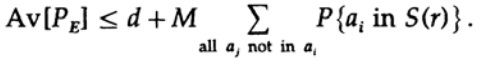
بالنسبة لأية رسالة معينة ، عند حساب متوسط ​​جميع دفاتر الكودك ، يعمل الترميز من خلال جميع القيم الممكنة ، لذا فإن متوسط ​​احتمال أن تكون النقطة في الكرة هي نسبة حجم الكرة إلى الحجم الكلي للمساحة. نطاق المجال



حيث يجب أن تكون s = Q + e2 <1/2 و ns عددًا صحيحًا.

المصطلح الأخير على اليمين هو الأكبر في هذا المبلغ. أولاً ، نحن نقدر قيمتها من خلال صيغة Stirling للعوامل. ثم ننظر إلى معامل اختزال الحد أمامه ، ونلاحظ أن هذا المعامل يزداد عند الانتقال إلى اليسار ، وبالتالي يمكننا: (1) تحديد قيمة المجموع إلى مجموع التقدم الهندسي مع هذا المعامل الأولي ، (2) توسيع التقدم الهندسي من أعضاء ns إلى عدد لانهائي من المصطلحات ، (3) احسب مجموع التقدم الهندسي اللامتناهي (الجبر القياسي ، لا شيء مهم) وأخيرًا احصل على القيمة الحدية (لعدد كبير بما فيه الكفاية n):



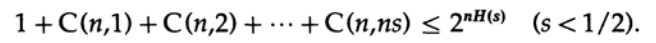
لاحظ كيف ظهرت الإنتروبيا H (s) في الهوية ذات الحدين. لاحظ أن التوسع في سلسلة Taylor H (s) = H (Q + e2) يعطي تقديرًا تم الحصول عليه مع مراعاة المشتق الأول فقط وتجاهل جميع المشتقات الأخرى. الآن دعنا نجمع التعبير النهائي:



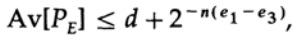
أين



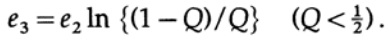
كل ما علينا فعله هو اختيار e2 بحيث يكون e3 <e1 ، وبعد ذلك سيكون الفصل الأخير صغيرًا بشكل تعسفي ، لأن n كبيرة بما يكفي. لذلك ، يمكن الحصول على متوسط ​​الخطأ PE بشكل تعسفي صغير بسعة قناة قريبة بشكل تعسفي من C.
إذا كان متوسط ​​جميع الرموز يحتوي على خطأ صغير بما فيه الكفاية ، فيجب أن يكون رمز واحد على الأقل مناسبًا ، وبالتالي ، يوجد نظام تشفير واحد مناسب على الأقل. هذه نتيجة مهمة حصل عليها شانون - "نظرية شانون لقناة ذات تداخل" ، على الرغم من أنه يجب ملاحظة أنه أثبتها في حالة أكثر عمومية بكثير من قناة ثنائية متناظرة بسيطة استخدمتها. بالنسبة للحالة العامة ، تكون الحسابات الرياضية أكثر تعقيدًا بكثير ، لكن الأفكار ليست مختلفة جدًا ، في كثير من الأحيان ، باستخدام مثال حالة خاصة ، يمكن للمرء أن يكشف عن المعنى الحقيقي للنظرية.

دعونا ننتقد النتيجة. كررنا مرارا وتكرارا: "ن كبيرة". ولكن ما حجم ن؟ كبير جدًا جدًا ، إذا كنت تريد حقًا أن تكون قريبًا من عرض النطاق الترددي للقناة وتأكد من نقل البيانات الصحيح! كبير جدًا لدرجة أنك في الواقع سيتعين عليك الانتظار لفترة طويلة جدًا لتجميع رسالة من العديد من البتات لترميزها لاحقًا. في الوقت نفسه ، سيكون حجم قاموس الكود العشوائي ضخمًا (بعد كل شيء ، لا يمكن تمثيل هذا القاموس في شكل أقصر من القائمة الكاملة لجميع بت Mn ، في حين أن n و M كبيران جدًا)!

تتجنب رموز تصحيح الخطأ انتظار رسالة طويلة جدًا ، مع تشفيرها وفك تشفيرها اللاحقين من خلال دفاتر الرموز الكبيرة جدًا ، لأنها تتجنب دفاتر الرموز في حد ذاتها وتستخدم الحسابات التقليدية بدلاً من ذلك. في نظرية بسيطة ، تفقد هذه الرموز ، كقاعدة عامة ، قدرتها على الاقتراب من سعة القناة وتحافظ في الوقت نفسه على معدل خطأ منخفض إلى حد ما ، ولكن عندما يصحح الرمز عددًا كبيرًا من الأخطاء ، فإنها تظهر نتائج جيدة. بمعنى آخر ، إذا كنت تضع نوعًا من سعة القناة لتصحيح الخطأ ، فيجب عليك استخدام خيار تصحيح الخطأ معظم الوقت ، أي يجب إصلاح عدد كبير من الأخطاء في كل رسالة مرسلة ، وإلا فستفقد هذه السعة مقابل لا شيء.

علاوة على ذلك ، فإن النظرية التي تم إثباتها أعلاه لا تزال لا معنى لها! ويوضح أن أنظمة الإرسال الفعالة يجب أن تستخدم مخططات تشفير متطورة لسلاسل البتات الطويلة جدًا. مثال على ذلك الأقمار الصناعية التي طارت خارج الكوكب الخارجي. عندما يبتعدون عن الأرض والشمس ، يضطرون لتصحيح المزيد والمزيد من الأخطاء في كتلة البيانات: تستخدم بعض الأقمار الصناعية الألواح الشمسية ، والتي تعطي حوالي 5 واط ، والبعض الآخر يستخدم مصادر الطاقة الذرية التي تعطي نفس الطاقة تقريبًا.القوة الضعيفة لمصدر الطاقة ، وصغر حجم لوحات الإرسال والحجم المحدود للوحات الاستقبال على الأرض ، والمسافة الضخمة التي يجب أن تنتقل إليها الإشارة - كل هذا يتطلب استخدام رموز بمستوى عالٍ من تصحيح الأخطاء لبناء نظام اتصال فعال.

نعود إلى الفضاء n-dimensional الذي استخدمناه في الدليل أعلاه. عند مناقشته ، أظهرنا أن الحجم الكلي للكرة تقريبًا يتركز بالقرب من السطح الخارجي ، وبالتالي من شبه المؤكد أن الإشارة المرسلة ستكون موجودة على سطح الكرة المبنية حول الإشارة المستقبلة ، حتى مع نصف قطر صغير نسبيًا من هذا المجال. لذلك ، ليس من المستغرب أن تتحول الإشارة المستقبلة بعد تصحيح عدد كبير من الأخطاء بشكل عشوائي ، nQ ، إلى أنها قريبة بشكل تعسفي من الإشارة دون أخطاء. إن قدرة قناة الاتصال ، التي فحصناها سابقًا ، هي المفتاح لفهم هذه الظاهرة. يرجى ملاحظة أن هذه المجالات التي تم إنشاؤها لرموز تصحيح خطأ هامينج لا تتداخل. عدد كبير من القياسات المتعامدة عمليا في عرض الفضاء الابعادلماذا يمكننا وضع الكرات M في الفضاء مع تداخل طفيف. إذا سمحت بتداخل صغير وصغير بشكل تعسفي ، والذي يمكن أن يؤدي فقط إلى عدد صغير من الأخطاء أثناء فك التشفير ، يمكنك الحصول على ترتيب كثيف من المجالات في الفضاء. يضمن هامينج مستوى معينًا من تصحيح الخطأ ، شانون - احتمال منخفض للخطأ ، ولكن في نفس الوقت الحفاظ على عرض النطاق الترددي الفعلي قريبًا بشكل تعسفي من سعة قناة الاتصال ، والتي لا يمكن لرموز هامينج القيام بها.ولكن في الوقت نفسه ، فإن الحفاظ على الإنتاجية الفعلية يقترب بشكل تعسفي من سعة قناة الاتصال ، وهو ما لا يمكن لرموز هامينغ القيام به.ولكن في الوقت نفسه ، فإن الحفاظ على الإنتاجية الفعلية يقترب بشكل تعسفي من سعة قناة الاتصال ، وهو ما لا يمكن لرموز هامينغ القيام به.

لا تتحدث نظرية المعلومات عن كيفية تصميم نظام فعال ، لكنها تشير إلى اتجاه الحركة نحو أنظمة اتصال فعالة. هذه أداة قيمة لبناء أنظمة الاتصال بين الأجهزة ، ولكن ، كما ذكرنا سابقًا ، ليس لها علاقة كبيرة بكيفية تبادل الأشخاص للمعلومات مع بعضهم البعض. إن مدى تشابه الوراثة البيولوجية مع أنظمة الاتصالات التقنية غير معروف ببساطة ، لذلك ليس من الواضح حاليًا كيف تنطبق نظرية المعلومات على الجينات. ليس لدينا خيار سوى المحاولة ، وإذا أظهر لنا النجاح الطبيعة الشبيهة بالآلة لهذه الظاهرة ، فإن الفشل سيشير إلى جوانب مهمة أخرى من طبيعة المعلومات.

دعنا لا نتشتت كثيرا. لقد رأينا أن جميع التعريفات الأولية ، إلى حد أكبر أو أقل ، يجب أن تعبر عن جوهر معتقداتنا الأولية ، ولكنها تتميز بدرجة معينة من التشويه ، وبالتالي فهي غير قابلة للتطبيق. من المقبول تقليديًا أن التعريف الذي نستخدمه في النهاية يحدد الجوهر ؛ لكنها تخبرنا فقط عن كيفية معالجة الأشياء ولا تجعلنا بأي معنى. النهج اللاحق ، الذي حظي بشهرة كبيرة في الأوساط الرياضية ، يترك الكثير مما هو مرغوب فيه في الممارسة.

سنلقي الآن نظرة على مثال لاختبارات الذكاء ، حيث يكون التعريف دوريًا كما تريد ، ونتيجة لذلك يضللك. يتم إنشاء اختبار من المفترض أن يقيس الذكاء. بعد ذلك ، تتم مراجعتها لتكون متسقة قدر الإمكان ، ثم يتم نشرها ومعايرتها بطريقة بسيطة بحيث يتم توزيع "الذكاء" المقاس بشكل طبيعي (بالطبع ، على طول منحنى المعايرة). يجب التحقق من جميع التعاريف ، ليس فقط عندما يتم اقتراحها لأول مرة ، ولكن بعد ذلك بكثير ، عندما يتم استخدامها في الاستنتاجات التي تم التوصل إليها. إلى أي مدى تعد حدود التعريف مناسبة للمهمة المطروحة؟ كم مرة يبدأ تطبيق التعاريف الواردة في نفس الشروط في ظروف مختلفة تمامًا؟ هذا أمر شائع بما فيه الكفاية!في العلوم الإنسانية التي ستواجهها حتمًا في حياتك ، يحدث هذا في كثير من الأحيان.

وبالتالي ، كان أحد أهداف هذا العرض لنظرية المعلومات ، بالإضافة إلى إثبات فائدتها ، هو تحذيرك من هذا الخطر ، أو توضيح كيفية استخدامه للحصول على النتيجة المرجوة. لقد لوحظ منذ فترة طويلة أن التعريفات الأولية تحدد ما تجده في النهاية إلى حد أكبر بكثير مما يبدو. تتطلب التعريفات الأولية اهتمامًا كبيرًا ليس فقط في أي موقف جديد ، ولكن أيضًا في المناطق التي تعمل بها لفترة طويلة. سيسمح لك هذا بفهم إلى أي مدى تكون النتائج التي تم الحصول عليها حشوًا ، وليس شيئًا مفيدًا.

, . , , , ! , .

...

, — magisterludi2016@yandex.ru

, — «The Dream Machine: » )

, , . ( 10 , 20 )