على نحو متزايد ، لاحظت أن الأشخاص العصاميين عصاميًا يفتقرون بالفعل إلى العتاد. يعرف الجميع اللغات ، لكن الأساسيات القليلة مثل أنواع البيانات أو الخوارزميات. قليلا عن أنواع البيانات.
في عام 1976 ، كتب العالم السويسري
نيكلاوس ويرث كتاب
الخوارزميات + هياكل البيانات = البرامج.بعد 40 عامًا ، لا تزال هذه المعادلة صحيحة. وإذا كنت شخصًا متعلمًا ذاتيًا واستعرضت المقالة لفترة طويلة في البرمجة ، فيمكنك ذلك قطريًا. يمكنك ترميز القهوة.

ستحتوي المقالة أيضًا على أسئلة يمكنك سماعها في المقابلة.
ما هو هيكل البيانات؟
بنية البيانات هي حاوية تقوم بتخزين البيانات في تخطيط معين. يسمح هذا "التخطيط" ببنية البيانات لتكون فعالة في بعض العمليات وغير فعالة في عمليات أخرى.
التي هناك؟
خطي ، تشكل العناصر تسلسلًا أو قائمة خطية ، وتجاوز العقد خطية. أمثلة: المصفوفات. قائمة مرتبطة ، مكدسات وطوابير.
غير خطي إذا كان تجاوز العقد غير خطي ، والبيانات ليست متسلسلة مثال: الرسم البياني والأشجار.
هياكل البيانات الأساسية.
- المصفوفات
- الأكوام
- قوائم الانتظار
- قوائم ذات صلة
- التهم
- الأشجار
- أشجار البادئة
- تجزئة الجدول
المصفوفات
الصفيف هو أبسط هيكل للبيانات وأكثرها استخدامًا. يتم اشتقاق تراكيب البيانات الأخرى ، مثل المداخن وقوائم الانتظار ، من المصفوفات.
صورة لمجموعة بسيطة من الحجم 4 تحتوي على عناصر (1 و 2 و 3 و 4).

يتم تعيين قيمة رقمية موجبة (فهرس) لكل عنصر بيانات ، وهو ما يتوافق مع موضع العنصر في الصفيف. تحدد معظم اللغات فهرس البداية للمصفوفة على أنه 0.
يوجد
أحادي البعد ، كما هو موضح أعلاه.
صفائف
متعددة الأبعاد ، داخل صفائف.
العمليات الأساسية
- إدراج إدراج عنصر في فهرس معين
- إحضار عنصر في فهرس معين
- حذف - حذف عنصر في فهرس معين
- الحجم - احصل على العدد الإجمالي للعناصر في المصفوفة
الأسئلة
- ابحث عن عنصر الصفيف الثاني الأدنى
- أول أعداد صحيحة غير متكررة في صفيف
- ادمج صفيفين مفروزين
- إعادة ترتيب القيم الموجبة والسالبة في صفيف
الأكوام
المكدس هو نوع بيانات مجردة ، وهو عبارة عن قائمة بالعناصر المنظمة وفقًا لمبدأ LIFO (أخيرًا - يخرج أولاً ، يخرج أخيرًا - يخرج أولاً).
هذه ليست صفائف. هذا هو الدور.
ابتكره آلان تورينج.مثال على المكدس سيكون حفنة من الكتب مرتبة عموديا. من أجل الحصول على الكتاب ، الموجود في مكان ما في المنتصف ، ستحتاج إلى حذف جميع الكتب الموضوعة عليه. هذه هي طريقة عمل طريقة LIFO (Last In First Out). تعمل وظيفة "إلغاء" في التطبيقات على LIFO.
صورة المكدس ، في ثلاثة عناصر (1 و 2 و 3) ، حيث يوجد 3 في الأعلى وسيتم حذفه أولاً.

العمليات الأساسية
- إدراج إدراج عنصر في الأعلى
- إرجاع Pop العنصر العلوي بعد إزالته من المكدس
- isEmpty-return true إذا كان المكدس فارغًا
- أعلى إرجاع العنصر العلوي بدون حذف من المكدس
الأسئلة
- تنفيذ قائمة انتظار باستخدام المكدس
- فرز القيم في المكدس
- تنفيذ مكدسين في صفيف
- اعكس سلسلة باستخدام مكدس
قوائم الانتظار
مثل المداخن ، تقوم قائمة الانتظار بتخزين عنصر بطريقة تسلسلية. اختلاف كبير عن المكدس هو استخدام FIFO (First in First Out) بدلاً من LIFO.
مثال على الخط هو خط من الناس. هذا الأخير أخذ الأخير وأنت ، والأولى ستتركها أولاً.
صورة قائمة الانتظار ، في أربعة عناصر (1 و 2 و 3 و 4) ، حيث يوجد 1 في الأعلى وسيتم حذفه أولاً

العمليات الأساسية
- Enqueue—) - إدراج عنصر في نهاية قائمة الانتظار
- Dequeue () - يزيل عنصرًا من بداية قائمة الانتظار
- isEmpty () - إرجاع صحيح إذا كانت قائمة الانتظار فارغة
- أعلى () - إرجاع العنصر الأول في قائمة الانتظار
الأسئلة
- تنفيذ مكدس باستخدام قائمة انتظار
- عكس عناصر N الأولى من قائمة الانتظار
- إنشاء أرقام ثنائية من 1 إلى N باستخدام قائمة انتظار
قائمة مرتبطة
القائمة المرتبطة هي صفيف حيث يكون كل عنصر كائنًا منفصلاً ويتكون من عنصرين - بيانات ورابط إلى العقدة التالية.
الميزة الأساسية على الصفيف هي المرونة الهيكلية: قد لا يتطابق ترتيب عناصر القائمة المرتبطة مع ترتيب موقع عناصر البيانات في ذاكرة الكمبيوتر ، ويتم تحديد ترتيب اجتياز القائمة بشكل صريح دائمًا من خلال علاقاتها الداخلية.
يوجد
في كل
اتجاه ، تقوم كل عقدة بتخزين العنوان أو الارتباط بالعقدة التالية في القائمة بينما تحتوي العقدة الأخيرة على العنوان أو الارتباط التالي كـ NULL.
1-> 2-> 3-> 4-> NULL
ثنائي الاتجاه ،
ارتباطان مرتبطان بكل عقدة ، واحدة من النقاط القوية للعقدة التالية وأخرى للعقدة السابقة.
NULL <-1 <-> 2 <-> 3-> NULL
دائري ، يتم توصيل جميع العقد لتشكيل دائرة. في النهاية ليس هناك NULL. قد تكون القائمة المرتبطة بالدورية قائمة مرتبطة بدورية مفردة أو مزدوجة.
1-> 2-> 3-> 1
القائمة الخطية أحادية الاتجاه الأكثر شيوعًا. على سبيل المثال نظام الملفات.

العمليات الأساسية
- InsertAtEnd - إدراج العنصر المحدد في نهاية القائمة.
- InsertAtHead - إدراج عنصر في أعلى القائمة
- حذف - يزيل العنصر المحدد من القائمة.
- DeleteAtHead - حذف العنصر الأول من القائمة
- بحث - لإرجاع العنصر المحدد من القائمة
- isEmpty - إرجاع True إذا كانت القائمة المرتبطة فارغة
الأسئلة
- عكس القائمة المرتبطة
- تحديد حلقة في قائمة مرتبطة
- إرجاع عنصر N من النهاية في القائمة المرتبطة
- إزالة التكرارات من قائمة مرتبطة
التهم
الرسم البياني عبارة عن مجموعة من العقد (الذروات) المتصلة ببعضها البعض في شكل شبكة بواسطة الحواف (الأقواس).
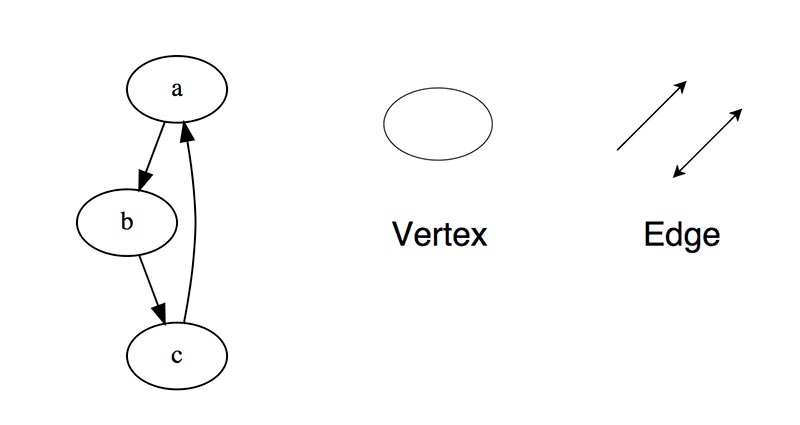
يوجد
موجه ، الأضلاع هي اتجاهية ، أي يوجد اتجاه واحد متاح فقط بين ذروتين متصلتين.
غير موجه ، لكل ضلوع يمكنك الذهاب في كلا الاتجاهين.
مختلط
وجدت في أشكال مثل
- مصفوفة المجاورة
- قائمة المجاورة
خوارزميات اجتياز الرسم البياني العام
- عرض البحث - مستوى الزحف
- البحث في العمق - اجتياز القمم
الأسئلة
- تنفيذ البحث في العرض والعمق
- تحقق مما إذا كان الرسم البياني شجرة أم لا
- عد عدد الحواف في الرسم البياني
- ابحث عن أقصر مسار بين القمتين
الأشجار
الشجرة هي بنية بيانات هرمية تتكون من العقد (القمم) والحواف (الأقواس). الأشجار هي رسوم بيانية متصلة بشكل أساسي بدون حلقات.
هياكل الشجرة في كل مكان. الجميع يعرف شجرة المهارات في الألعاب.
شجرة بسيطة
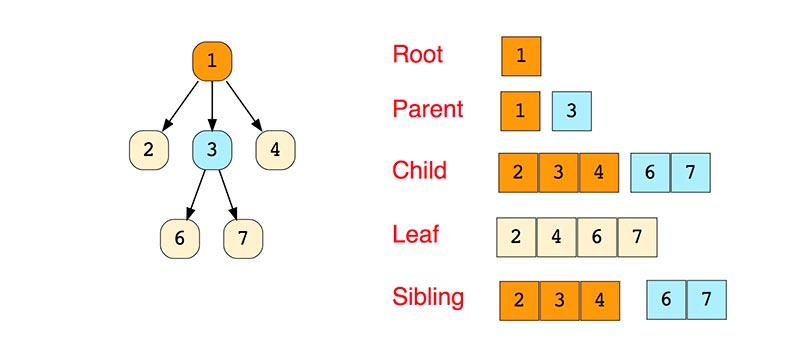
أنواع الأشجار
الشجرة الثنائية هي الأكثر شيوعًا.
"الشجرة الثنائية هي بنية بيانات هرمية يكون لكل عقدة فيها قيمة (وهي أيضًا المفتاح في هذه الحالة) وإشارات إلى السليل الأيسر والأيمن. »- بروكسثلاث طرق للتجول في الشجرة
- بالترتيب المباشر (من الأعلى إلى الأسفل) - نموذج البادئة.
- بترتيب متماثل (من اليسار إلى اليمين) - شكل معلومات.
- في الترتيب العكسي (من الأسفل إلى الأعلى) - نموذج postfix.
الأسئلة
- أوجد ارتفاع شجرة ثنائية
- ابحث عن أصغر عنصر N في شجرة بحث ثنائية
- ابحث عن العقد على مسافة N من الجذر
- ابحث عن أسلاف العقدة N في شجرة ثنائية
تري (شجرة بادئة)
نوع من شجرة للسلاسل ، بحث سريع. قواميس T9
هكذا تخزن هذه الشجرة الكلمات "العليا" و "هكذا" و "الخاصة بهم".

يتم تخزين الكلمات من الأعلى إلى الأسفل ، وتشير العقد الخضراء "p" و "s" و "r" إلى نهاية "top" و "وهكذا" و "بهم" ، على التوالي.
الأسئلة
- عد العدد الإجمالي للكلمات
- اطبع كل الكلمات
- فرز عناصر الصفيف من شجرة البادئة
- إنشاء قاموس T9
تجزئة الجدول
التجزئة هي عملية تستخدم لتعريف الكائنات بشكل فريد وتخزين كل كائن في فهرس فريد (مفتاح) محسوب مسبقًا.
يتم تخزين الكائن كزوج قيمة مفتاح ، وتسمى مجموعة من هذه العناصر القاموس. يمكن العثور على كل كائن باستخدام هذا المفتاح.
في الأساس ، هذا هو صفيف يتم فيه تمثيل المفتاح كدالة تجزئة.
يعتمد أداء التجزئة على التجزئة
- وظائف التجزئة
- تجزئة حجم الجدول
- طرق إدارة التصادم
مثال على تطابق التجزئة في المصفوفة. يتم حساب فهرس هذا الصفيف من خلال دالة التجزئة.

الأسئلة
- ابحث عن أزواج متماثلة في مصفوفة
- ابحث عما إذا كان الصفيف مجموعة فرعية من صفيف آخر
- وصف التجزئة المفتوحة
قائمة الموارد
بدلا من الاستنتاج
العتاد مثير مثل اللغات نفسها. ربما يرى شخص ما الهياكل الأساسية المألوفة لديه ويكون مهتمًا.
شكرا للقراءة. أتمنى ألا تضيع الوقت =)
ملحوظة: أعتذر ، كما اتضح فيما بعد ، أن ترجمة المقال كانت موجودة بالفعل ، وقد تم تجاهلها مؤخرًا.
إذا كانت مهتمة ،
ها هي ، شكرا
Hokum ، سأكون أكثر حذرا.