اختبئ بدون اختباء. مرة أخرى حول إخفاء المعلومات LSB ، خي مربع و ... التفرد؟

اليوم ، سنعرض العش القديم مرة أخرى ونتحدث عن كيفية إخفاء مجموعة من القطع في الصورة مع قطة ، وإلقاء نظرة على العديد من الأدوات المتاحة وتحليل أكثر الهجمات شيوعًا. ويبدو أن ما علاقة التفرد بها؟

كما يقولون ، إذا كنت تريد معرفة شيء ما ، فاكتب مقالًا عنه على هبر! (تحذير ، الكثير من النصوص والصور)



علم إخفاء المعلومات (حرفيا من "التشفير" اليوناني) هو علم نقل البيانات المخفية (رسائل stego) في البيانات المفتوحة الأخرى (stegocontainers) مع إخفاء حقيقة نقل البيانات. لا تقلق ، في الواقع ، كل شيء ليس معقدًا للغاية.

لذا ، أين في الصورة يمكنك إخفاء الرسالة بحيث لا يلاحظ أحد؟

وهناك مكانان فقط: البيانات الوصفية والصورة نفسها. هذا الأخير بسيط للغاية ، فقط اكتب "exif" على Google. لذلك دعونا نبدأ على الفور مع الثاني.

بت أقل أهمية

نموذج الألوان الأكثر شيوعًا هو RGB ، حيث يتم تمثيل اللون على شكل ثلاثة مكونات: الأحمر والأخضر والأزرق . يتم تشفير كل مكون في الإصدار الكلاسيكي باستخدام 8 بت ، أي أنه يمكن أن يأخذ قيمة من 0
إلى 255. ومن هنا يخفي البت الأقل أهمية. من المهم أن نفهم أن لون RGB واحد يمثل ثلاثة بتات من هذا القبيل.

لتقديمها بشكل أكثر وضوحًا ، سنقوم ببعض التلاعبات الصغيرة.

كما وعد ، التقط صورة لقطة بتنسيق png.



نقسمها إلى ثلاث قنوات وفي كل قناة نأخذ أقل جزء مهم. قم بإنشاء ثلاث صور جديدة ، حيث تشير كل بكسل إلى NZB. صفر - البيكسل أبيض ، والوحدة سوداء على التوالي.

نحصل على هذا.




ولكن ، كقاعدة عامة ، يتم العثور على الصورة في "النموذج المجمع". لتمثيل NZB للمكونات الثلاثة في صورة واحدة ، يكفي استبدال المكون في بكسل حيث يكون NZB وحدة ، واستبداله بـ 255 ، واستبداله بـ 0.

ولكن ليس أقل أهمية

تخيل أن كل ما رأيناه في الصورة الأخيرة هو لنا ولدينا الحق في فعل أي شيء به. ثم نأخذها كتدفق من البتات ، حيث يمكننا القراءة وأين يمكننا الكتابة.

نأخذ البيانات التي نريد أن نتقاطع في الصورة ، ونقدمها في شكل بتات ونكتبها بدلاً من تلك الموجودة.

لاستخراج هذه البيانات ، نقرأ NZB على شكل دفق البت وإحضاره إلى النموذج المطلوب. لمعرفة عدد البتات المطلوب حسابها ، كقاعدة ، تتم كتابة حجم الرسالة في البداية. ولكن هذه تفاصيل التنفيذ.

وتجدر الإشارة إلى أنه في حوالي 50٪ من الحالات ، سيتزامن الجزء الذي نريد كتابته والجزء الموجود في الصورة ولن نضطر إلى تغيير أي شيء.

هذا كل شيء ، تنتهي الطريقة هنا.

لماذا يعمل؟

ألق نظرة على الصور أدناه.

هذا هو stegocontainer فارغ:



وهذا 95٪ ممتلئ:



ترى الفرق؟ لكنها هي. لماذا ذلك

دعونا نلقي نظرة على لونين: (0 ، 0 ، 0) و (1 ، 1 ، 1) ، أي أن الألوان تختلف فقط عن NZB في كل مكون.



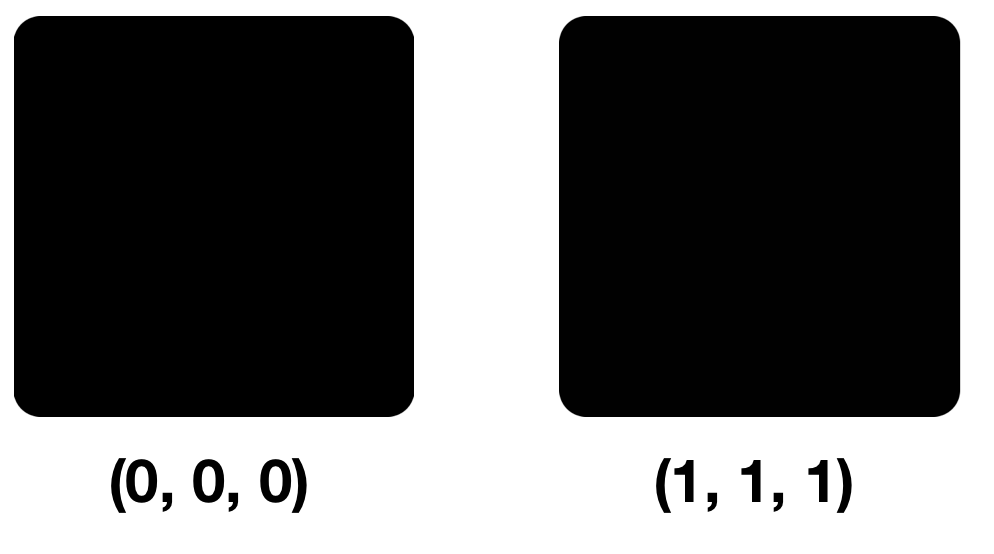
لن تكون هناك اختلافات طفيفة في وحدات البكسل عند اللمحة الأولى والثانية والثالثة. والحقيقة هي أن أعيننا يمكن أن تميز حوالي 10 مليون لون ، والدماغ حوالي 150 فقط. يحتوي نموذج RGB أيضًا على 16777216 لونًا. يمكنك محاولة تمييزهم جميعًا هنا.

من سطر الأوامر

لا تتوفر العديد من أدوات سطر الأوامر مفتوحة المصدر التي تمثل إخفاء معلومات LSB.

يمكن العثور على الأكثر شعبية في الجدول أدناه.

اين القطة؟

والأول في قائمة الهجمات على إخفاء معلومات LSB هو هجوم مرئي. يبدو غريبا ، أليس كذلك؟ بعد كل شيء ، القطة بسر لم تخون نفسها كمحمية مملوءة للوهلة الأولى. هممم ... أنت فقط بحاجة إلى معرفة مكان البحث. من السهل تخمين أن NZB فقط يستحق اهتمامنا الوثيق.

بالنسبة إلى stegocontainer المعبأ ، تبدو الصورة مع NZB كما يلي:



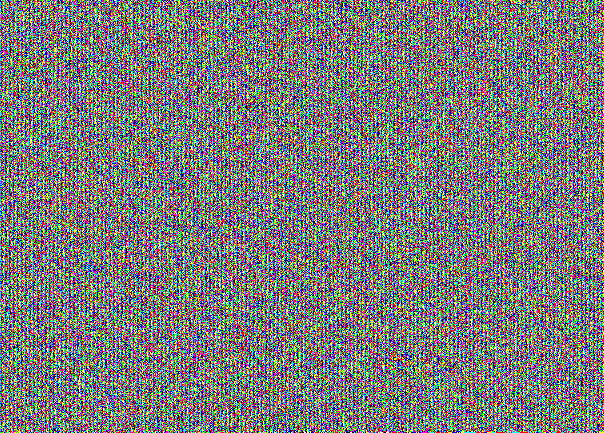
لا تصدق؟ هنا لديك NZB من جميع القنوات الثلاث بشكل منفصل:




هذا "رسم" خاص لإخفاء الرسالة في NZB. للوهلة الأولى ، يبدو هذا كضجيج بسيط. ولكن عند النظر إلى الهيكل يكون مرئيًا. هنا يمكنك أن ترى أن stegocontainer ممتلئ. إذا أخذنا رسالة بنسبة 30٪ من قدرة قطة فقيرة ، فسوف نحصل على هذه الصورة:


له NZB:



~ 70٪ من القطة تبقى دون تغيير.

هنا يجدر عمل استطراد صغير والحديث عن الأحجام. ما هو القط 30٪؟ حجم القطة 603x433 بكسل. 30٪ من هذا الحجم 78459 بكسل. يحتوي كل بكسل على 3 بتات من المعلومات. مجموع 78459 3 = 235377 بت أو أقل بقليل من 30 كيلوبايت يناسب 30٪ من الختم. وستصل القطة بأكملها إلى حوالي 100 كيلو بايت. مثل هذه الأشياء.

لكننا هنا من أجلك لسبب ما. فكيف لخداع العيون؟
الفكرة الأولى: إلصاق الرسالة بالضوضاء. لكنها لم تكن هناك. التالي هو جزء من stegocontainer المعبأ و LSB الخاص به.



مع القليل من الجهد ، لا يزال بإمكاننا تمييز بنية مألوفة. لا تفقدوا الأمل أيها السادة!

هه هه هه

الكثير من الأشياء تكسر الإحصائيات ، كما تعلم.

تغيير شيء في الصورة ، نقوم بتغيير خصائصه الإحصائية. يكفي أن يجد المحلل طريقة لإصلاح هذه التغييرات.

بدأ Andreas Wesfield و Andreas Pfitzmann من جامعة دريسدن في ساحة خي القديمة الجيدة في عملهم "Attacks on Steganographic Systems" ، والذي يمكن العثور عليه هنا.

في ما يلي ، سنتحدث عن الهجمات داخل نفس مستوى اللون ، أو في سياق RGB ، حول الهجمات على قناة واحدة. يمكن تقليل نتائج كل هجوم إلى المتوسط ​​والحصول على نتيجة للصورة "المجمعة".

لذا ، فإن هجوم Chi-square يعتمد على افتراض أن احتمال ظهور الألوان المجاورة (التي تختلف باختلاف البت الأقل دلالة) (زوج من القيم) في حاوية فارغة فارغة صغير للغاية. إنه حقًا ، يمكنك تصديقه. بمعنى آخر ، يختلف عدد البكسل بلونين متجاورين بشكل كبير بالنسبة للحاوية الفارغة. كل ما نحتاجه هو حساب عدد وحدات البكسل لكل لون وتطبيق صيغتين. في الواقع ، هذه مهمة بسيطة لاختبار فرضية باستخدام اختبار خي مربع.

القليل من الرياضيات؟

دع h يكون مصفوفة في المكان الأول الذي يحتوي على عدد بكسل اللون الأول في الصورة قيد الدراسة.

ثم:

1. تردد اللون المقاس $$$i = 2k$ :
   

   $$

   $$n_k = h [2k] ، ~ k \ في [0 ، 127] ؛$$
   
   
2. تردد اللون المتوقع نظريًا $$$i = 2k$ :
   

   $$

   $$n_k ^ * = \ frac {h [2k] + h [2k + 1]} {2}، ~ k \ in [0،127]؛$$
   
   

ستؤدي ترجمة هذا إلى Python إلى شيء من هذا القبيل:

for k in range(0, len(histogram) // 2): expected.append(((histogram[2 * k] + histogram[2 * k + 1]) / 2)) observed.append(histogram[2 * k]) 

حيث الرسم البياني هو عدد بكسلات اللون i في الصورة ، $$$i \ in [0، 255]$

يتم حساب معيار خي مربع لعدد درجات الحرية k-1 على النحو التالي (k هو عدد الألوان المختلفة ، أي 256):

$$

$$\ chi_ {k-1} ^ 2 = \ sum_ {i = 1} ^ {k} \ frac {(n_k - n_k ^ *) ^ 2} {n_k ^ *} ؛$$

وأخيرًا P هو احتمال أن التوزيعات $$$n_i$ و $$$n_i ^ *$ في ظل هذه الظروف متساوون (احتمال أن يكون لدينا stegocontainer مليء). يتم حسابها من خلال دمج وظيفة النعومة:

$$

$$P = 1 - \ frac {1} {2 ^ {\ frac {k-1} {2}} \ Gamma (\ frac {k-1} {2})} \ int_0 ^ {\ chi_ {k-1 } ^ 2} e ^ {- \ frac {x} {2}} x ^ {\ frac {k-1} {2} -1} dx؛$$

من الأكثر فعالية تطبيق مربع خيالي ليس على الصورة بأكملها ، ولكن فقط على أجزائها ، على سبيل المثال ، على الخطوط. إذا كان الاحتمال المحسوب للخط أكبر من 0.5 ، فاملأ الخط في الصورة الأصلية باللون الأحمر. إذا كان أقل ، ثم أخضر. بالنسبة للقطط الممتلئة بنسبة 30٪ ، ستبدو الصورة كما يلي:



صحيح تمامًا ، أليس كذلك؟

حسنًا ، لقد حصلنا على هجوم سليم رياضيًا ، ولا يمكنك خداع الرياضيات! أم ... ؟؟

رقص عشوائي

الفكرة بسيطة للغاية: لا تكتب البتات بالترتيب ، ولكن في أماكن عشوائية. للقيام بذلك ، تحتاج إلى أخذ PRSP ، وتكوينه لإصدار نفس الدفق العشوائي مع نفس الجانب (الملقب بكلمة المرور). بدون معرفة كلمة المرور ، لن نتمكن من تكوين PRNG والعثور على وحدات البكسل التي تم إخفاء الرسالة فيها. سوف نقوم باختباره على قطة.

القطط (الانتهاء 32 ٪):



LSB له:



تبدو الصورة صاخبة ، ولكنها ليست مشبوهة لمحلل قليل الخبرة. ماذا يقول مربع كاي؟


يبدو أن القبعة السوداء فازت !؟ مهما ...

الانتظام - التفرد

طريقة إحصائية أخرى كانت جيسيكا فريدريش وميروسلاف جوليان وأندرياس فيتزمان في عام 2001. تم تسميته كطريقة RS. يمكن أخذ المقالة الأصلية هنا.

تحتوي الطريقة على عدة خطوات تحضيرية.

تنقسم الصورة إلى مجموعات من n بكسل. على سبيل المثال ، 4 وحدات بكسل متتالية على التوالي. كقاعدة ، تحتوي هذه المجموعات على وحدات بكسل متجاورة.
بالنسبة لقطتنا مع ملء متسلسل في القناة الحمراء ، ستكون المجموعات الخمس الأولى:

• [78 ، 78 ، 79 ، 78]
  
• [78 ، 78 ، 78 ، 78]
  
• [78 ، 79 ، 78 ، 79]
  
• [79 ، 76 ، 79 ، 76]
  
• [76 ، 76 ، 76 ، 77]
  

(جميع القياسات في الإصدار الكلاسيكي من RGB)

ثم نحدد ما يسمى بوظيفة التمايز أو دالة النعومة ، التي تقوم بتعيين كل مجموعة من وحدات البكسل إلى عدد حقيقي. الغرض من هذه الوظيفة هو التقاط نعومة أو "انتظام" مجموعة البكسل G. كلما كانت مجموعة البكسل أكثر ضوضاء $$$G = (x_1، ...، x_n)$ ، كلما كانت الوظيفة التمييزية أكثر أهمية. في معظم الأحيان ، يتم اختيار "اختلاف" مجموعة وحدات البكسل ، أو ببساطة أكثر ، مجموع الاختلافات في وحدات البكسل المجاورة في المجموعة. ولكن أيضًا يمكن أن تأخذ في الاعتبار الافتراضات الإحصائية حول الصورة.

$$

$$f (x_1، x_2، ...، x_n) = \ sum_ {i = 1} ^ {n-1} | x_ {i + 1} - x_i |$$

قيم دالة النعومة لمجموعة من وحدات البكسل من مثالنا:

• و (78 ، 78 ، 79 ، 78) = 2
• و (78 ، 78 ، 78 ، 78) = 0
• و (78 ، 79 ، 78 ، 79) = 3
• و (79 ، 76 ، 79 ، 76) = 9
• و (76 ، 76 ، 76 ، 77) = 1

بعد ذلك ، يتم تحديد فئة وظائف التقليب من بكسل واحد.

يجب أن يكون لديهم بعض الخصائص.

$$

$$1. ~~~ \ forall x \ in P: ~ F (F (x)) = x، ~~ P = \ {0، ~ 255 \}؛$$

$$

$$2. ~~~ F_1: 0 \ leftrightarrow 1 ، ~ 2 \ leftrightarrow 3 ، ~ ... ، 254 \ leftrightarrow 255 ؛$$

$$

أين $$$F$ - أي وظيفة من فئة واحدة ، $$$F_1$ هي وظيفة التقليب المباشر ، و $$$F _ {- 1}$ - عكس. بالإضافة إلى ذلك ، عادة ما يشار إلى وظيفة التقليب المتطابقة $$$F_0$ الذي لا يغير بكسل.

قد تبدو وظائف التقليب الثعباني مثل هذا:

 def flip(val): if val & 1: return val - 1 return val + 1 def invert_flip(val): if val & 1: return val + 1 return val - 1 def null_flip(val): return val 

لكل مجموعة من وحدات البكسل ، نقوم بتطبيق إحدى وظائف التقليب واستناداً إلى قيمة الوظيفة التمييزية قبل التقليب وبعده ، نحدد نوع مجموعة البكسل: عادي ( R egular) ، فردي / غير عادي ( S ingular) ، وغير قابل للاستخدام. نظرًا لعدم استخدام النوع الأخير بشكل أكبر ، تم تسمية الطريقة بعد الأحرف الأولى من أنواع المفاتيح. هذا هو سر الاسم بالكامل ، التفرد ليس له علاقة به :)



قد نرغب في تطبيق تقليب مختلف على وحدات البكسل المختلفة ، لذلك نحدد قناع M بقيم n من -1 أو 0 أو 1.

$$

$$F_M (G) = (F_ {M (1)} (x_1) ، F_ {M (2)} (x_2) ، ... ، F_ {M (n)} (x_n))$$

ليكن القناع الخاص بمثالنا كلاسيكيًا - [1، 0، 0، 1]. وجد تجريبيا أن الأقنعة المتناظرة التي لا تحتوي عليها $$$F _ {- 1}$ . من الخيارات الناجحة أيضًا: [0 ، 1 ، 0 ، 1] ، [0 ، 1 ، 1 ، 0] ، [1 ، 0 ، 1 ، 0]. نطبق التقليب للمجموعات من المثال ، نحسب قيمة النعومة ونحدد نوع مجموعة البكسل:

• $$$F_m$ (78 ، 78 ، 79 ، 78) = [79 ، 78 ، 79 ، 79] ؛
  و (79 ، 78 ، 79 ، 79) = 2 = 2 = و (78 ، 78 ، 79 ، 78)
  مجموعة غير قابلة للاستخدام
  
  
• $$$F_m$ (78 ، 78 ، 78 ، 78) = [79 ، 78 ، 78 ، 79] ؛
  و (79 ، 78 ، 78 ، 79) = 2> 0 = و (78 ، 78 ، 78 ، 78)
  مجموعة عادية
  
  
• $$$F_m$ (78 ، 79 ، 78 ، 79) = [79 ، 79 ، 78 ، 78] ؛
  و (79 ، 79 ، 78 ، 78) = 1 <3 = f (78 ، 79 ، 78 ، 79) مجموعة فردية
  
  
• $$$F_m$ (79 ، 76 ، 79 ، 76) = [78 ، 76 ، 79 ، 77] ؛
  و (78 ، 76 ، 79 ، 77) = 7 <9 = f (79 ، 76 ، 79 ، 76) مجموعة فردية
  
  
• $$$F_m$ (76 ، 76 ، 76 ، 77) = [77 ، 76 ، 76 ، 76] ؛
  و (77 ، 76 ، 76 ، 76) = 1 = 1 = و (76 ، 76 ، 76 ، 77)
  مجموعة غير قابلة للاستخدام
  
  

نشير إلى عدد المجموعات المنتظمة للقناع M كـ $$$R_M$ (بالنسب المئوية لجميع المجموعات) ، و $$$S_M$ للمجموعات الفردية.

ثم $$$R_M + S_M \ leq 1$ و $$$R _ {- M} + S _ {- M} \ leq 1$ ، لقناع سالب (يتم ضرب جميع مكونات القناع في -1) ، لأن $$$R_M + S_M + U_M = 1$ بينما $$$U_M$ قد تكون فارغة. وبالمثل لقناع سلبي.

الفرضية الإحصائية الرئيسية هي أن القيمة المتوقعة في صورة نموذجية $$$R_M$ يساوي $$$R _ {- M}$ ، ونفس الشيء صحيح $$$S_M$ و $$$S _ {- M}$ . وقد ثبت ذلك من خلال البيانات التجريبية وبعض الرقصات مع الدف حول الخاصية الأخيرة لوظيفة التقليب.

$$

$$R_M \ cong S_M ~~~~ R _ {- M} \ cong S _ {- M}$$

دعونا نتحقق من ذلك في مثالنا الصغير؟ نظرًا لصغر حجم العينة ، قد لا نؤكد هذه الفرضية. دعونا نرى ما يحدث مع القناع المقلوب: [-1، 0، 0، -1].

• F_M (78 ، 78 ، 79 ، 78) = [77 ، 78 ، 79 ، 77] ؛
  و (77 ، 78 ، 79 ، 77) = 4> 2 = و (77 ، 78 ، 79 ، 77)
  مجموعة عادية
  
  
• F_M (78 ، 78 ، 78 ، 78) = [77 ، 78 ، 78 ، 77] ؛
  و (77 ، 78 ، 78 ، 77) = 2> 0 = و (78 ، 78 ، 78 ، 78)
  مجموعة عادية
  
  
• F_M (78 ، 79 ، 78 ، 79) = [77 ، 79 ، 78 ، 80] ؛
  و (77 ، 79 ، 78 ، 80) = 5> 3 = و (78 ، 79 ، 78 ، 79)
  مجموعة عادية
  
  
• F_M (79 ، 76 ، 79 ، 76) = [80 ، 76 ، 79 ، 75] ؛
  و (80 ، 76 ، 79 ، 75) = 11> 9 = و (79 ، 76 ، 79 ، 76)
  مجموعة عادية
  
  
• F_M (76 ، 76 ، 76 ، 77) = [75 ، 76 ، 76 ، 78] ؛
  و (75 ، 76 ، 76 ، 78) = 3> 1 = و (76 ، 76 ، 76 ، 77)
  مجموعة عادية
  
  

حسنًا ، كل شيء واضح.

لكن الفرق بين $$$R_M$ و $$$S_M$ تميل إلى الصفر مع زيادة طول m للرسالة المضمنة ونحصل على ذلك $$$R_M \ cong S_M$ .

من المضحك أن التوزيع العشوائي لمستوى LSB له تأثير معاكس على $$$R _ {- M}$ و $$$S _ {- M}$ . يزيد اختلافهم مع طول m للرسالة المضمنة. يمكن العثور على تفسير لهذه الظاهرة في المقالة الأصلية.

هذا هو الجدول الزمني $$$R_M$ ، $$$S_M$ ، $$$R _ {- M}$ و $$$S _ {- M}$ اعتمادًا على عدد البكسل مع LSBs المقلوبة ، يطلق عليه رسم تخطيطي RS. المحور x هو النسبة المئوية لوحدات البكسل مع LSB المقلوبة ، والمحور y هو العدد النسبي للمجموعات العادية والمفردة مع الأقنعة M و -M ، $$$M = [0 ~ 1 ~ 1 ~ 0]$ .



إن جوهر طريقة تحليل الغشاء المخاطي RS هو تقييم المنحنيات الأربعة لمخطط RS وحساب تقاطعها باستخدام الاستقراء. لنفترض أن لدينا stegocontainer برسالة بطول غير معروف p (كنسبة مئوية من البكسل) مضمن في البتات السفلية لوحدات البكسل المحددة عشوائيًا (أي باستخدام RandomLSB). قياساتنا الأولية لعدد المجموعات R و S تتوافق مع النقاط $$$R_M (ص / 2)$ ، $$$S_M (ص / 2)$ ، $$$R _ {- M} (ص / 2)$ و $$$S _ {- M} (ص / 2)$ . نأخذ نقاطًا من نصف طول الرسالة تمامًا ، نظرًا لأن الرسالة عبارة عن دفق بت عشوائي ، وفي المتوسط ​​، كما ذكرنا سابقًا ، سيتم تغيير نصف البكسل فقط عن طريق تضمين الرسالة.

إذا قمنا بعكس LSB لجميع وحدات البكسل في الصورة وحسبنا عدد مجموعات R و S ، نحصل على أربع نقاط $$$R_M (1-ف / 2)$ ، $$$S_M (1-ف / 2)$ ، $$$R _ {- M} (1-p / 2)$ و $$$S _ {- M} (1-p / 2)$ . نظرًا لأن هاتين النقطتين تعتمدان على التوزيع العشوائي المحدد لـ LSB ، يجب علينا تكرار هذه العملية عدة مرات وتقييمها $$$R_M (1/2)$ و $$$S_M (1/2)$ من العينات الإحصائية.

يمكننا رسم الخطوط بشكل مشروط من خلال النقاط $$$R _ {- M} (ص / 2)$ ، $$$R _ {- M} (1-p / 2)$ و $$$S _ {- M} (ص / 2)$ ، $$$S _ {- M} (1-p / 2)$ .

النقاط $$$R_M (ص / 2)$ ، $$$R_M (1/2)$ ، $$$R_M (1-ف / 2)$ و $$$S_M (ص / 2)$ ، $$$S_M (1/2)$ ، $$$S_M (1-ف / 2)$ تحديد اثنين من القطع المكافئ. يتقاطع كل القطع المكافئ والخط المقابل على اليسار. يسمح لنا الوسط الحسابي للإحداثيات س لكلا التقاطعين بتقدير طول الرسالة غير المعروفة p.

لتجنب تقدير إحصائي طويل لنقاط المنتصف RM (1/2) و SM (1/2) ، يمكن أخذ بضعة اعتبارات أخرى:

1. نقطة تقاطع المنحنى $$$R_M$ و $$$R _ {- M}$ له نفس إحداثيات x عند نقطة تقاطع المنحنيات $$$S_M$ و $$$S _ {- M}$ . هذه في الأساس نسخة أكثر صرامة من فرضيتنا الإحصائية. (انظر أعلاه)
2. يتقاطع منحني RM و SM عند m = 50٪ ، أو $$$R_M (1/2) = S_M (1/2)$ .

يوفر هذان الافتراضان صيغة بسيطة لطول الرسالة السرية ص. بعد قياس المحور س بحيث يصبح p / 2 0 و 1 - p / 2 يصبح 1 ، فإن إحداثيات س لنقطة التقاطع هي جذر المعادلة التربيعية التالية



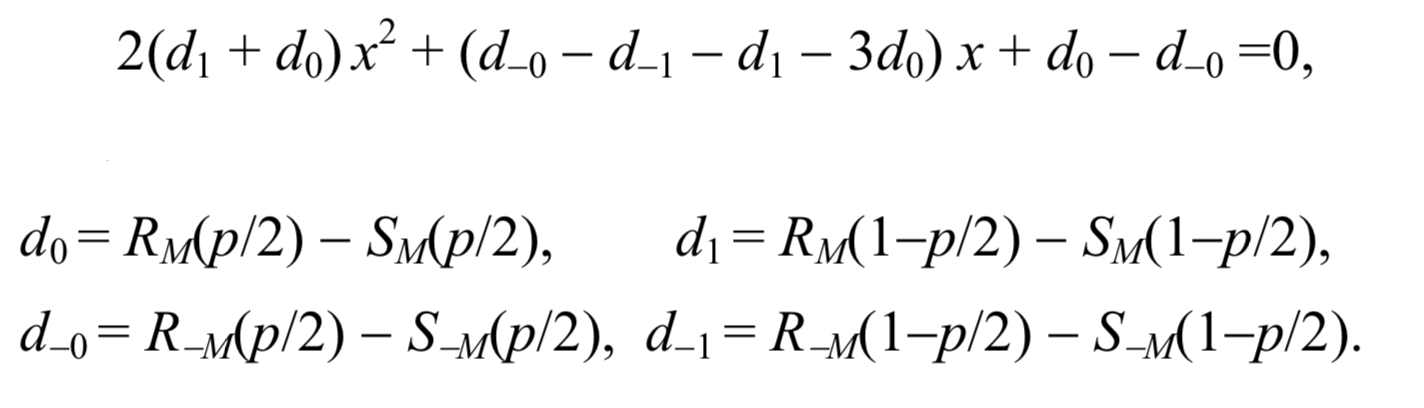
ثم يمكن حساب طول الرسالة بالصيغة:

$$

$$p = \ frac {x} {x- \ frac {1} {2}}$$

هنا تدخل قطتنا المشهد. (ألم يحن الوقت لإعطائه اسمًا؟)

لذلك لدينا:

• مجموعات RM العادية (ص / 2): 23121 قطعة.
• مجموعات SM المفردة (ص / 2): 14124 قطعة.
• المجموعات العادية ذات القناع المقلوب RM (p / 2): 37191 قطعة.
• مجموعات مفردة ذات قناع مقلوب SM (p / 2): 8440 قطعة.
• المجموعات العادية مع LSB RM المقلوب (1-p / 2): 20298 قطعة.
• مجموعات فردية مع LSB SM مقلوب (1-p / 2): 16206 قطعة.
• المجموعات العادية مع LSB المقلوب والقناع المقلوب RM (1-p / 2): 40603 جهاز كمبيوتر.
• مجموعات فردية مع LSB معكوس وقناع مقلوب SM (1-p / 2): 6947 قطعة.

(إذا كان لديك الكثير من وقت الفراغ ، فيمكنك حسابها بنفسك ، ولكن الآن أقترح عليك تصديق حساباتي)

على جدول الأعمال ، تركنا الرياضيات العارية. هل ما زلت تتذكر كيفية حل المعادلات التربيعية؟

$$

$$d_0 = 8997 دولا$$

$$

$$d _ {- 0} = 28751 دولارً$$

$$

$$d_1 = 4092 دولا$$

$$

$$d _ {- 1} = 33656$$

باستبدال كل d في الصيغة أعلاه ، نحصل على معادلة تربيعية ، والتي نحلها كما يتم تدريسها في المدرسة.

$$

$$26178x ^ 2-35988x - 19754 = 0$$

$$

$$D = (-35988) ^ 2 - 426178 * (- 19754) = $ 336361699$$

$$

$$x_1 = 1.7951 ~~~~~~~~ x_2 = -0.4204$$

خذ جذر معامل أصغر ، أي $$$x_2$ . ثم سيكون التقدير التقريبي للرسالة المضمنة في القط هو:

$$

$$p = \ frac {-0.4204} {- 0.4204 - 0.5} = 0.4567$$

نعم ، هذه الطريقة لها زائد كبير وناقص واحد كبير. الميزة هي أن الطريقة تعمل مع كل من إخفاء معلومات LSB العادي وإخفاء RandomLSB. لا يمكن لشي مربع أن يتباهى بهذه الفرصة. تعرفت الطريقة على قطتنا ذات المظهر العشوائي بدقة وقدرت طول الرسالة بـ 0.3256 ، وهو دقيق للغاية.

يكمن الطرح في الخطأ الكبير (الكبير جدًا) لهذه الطريقة ، والذي ينمو جنبًا إلى جنب مع الرسالة الطويلة مع التضمين المتسلسل . على سبيل المثال ، بالنسبة للقطة التي تشغل 30٪ ، فإن تنفيذي لهذه الطريقة يعطي تقديرًا تقريبيًا متوسطًا لثلاث قنوات من 0.4633 أو 46٪ من السعة الإجمالية ، مع إشغال أكثر من 95٪ - 0.8597. ولكن بالنسبة لقطة فارغة تصل إلى 0.0054. وهذا اتجاه عام مستقل عن التنفيذ. تعطي النتائج الأكثر دقة باستخدام طريقة LSB العادية طول الرسالة المضمنة 10٪ + - 5٪.

زائد أو ناقص

حتى لا يتم القبض عليك ، يجب أن يكون المرء غير متوقع ويستخدم ترميز ± 1. بدلاً من تغيير الجزء الأقل أهمية في بايت اللون ، سنقوم إما بزيادة أو تقليل البايت بأكمله بمقدار واحد. هناك استثناءان فقط:

• لا يمكننا تقليل الصفر ، لذلك سنزيده ،
  
• لا يمكننا أيضًا زيادة 255 ، لذلك سننقص هذه القيمة دائمًا.
  

بالنسبة لجميع قيم البايت الأخرى ، نختار عشوائيًا إما زيادة بمقدار واحد أو نقصان. علاوة على هذا التلاعب ، سيتغير LSB كما كان من قبل. لمزيد من الموثوقية ، من الأفضل أخذ وحدات بايت عشوائية لتسجيل رسالة.

هنا القط صديقنا:



ظاهريا ، المقدمة غير محسوسة بالضبط لنفس السبب الذي يجعل الفروق بين (0 ، 0 ، 0) و (1 ، 1 ، 1) غير مرئية.



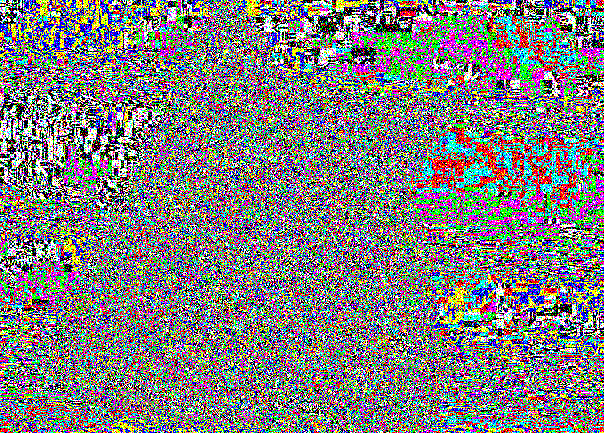
تظل شريحة LSB صاخبة ببساطة بسبب التسجيل في أماكن عشوائية.



لا يزال مربع كاي أعمى ، وتعطي طريقة RS تقديرًا تقريبيًا يبلغ 0.0036 .

لكي لا تكون سعيدا جدا ، اقرأ هذا المقال هنا.

قد يسأل أكثرها انتباهًا كيف يمكننا الحصول على رسالة إذا تم تغيير وحدات البايت بأكملها بشكل عشوائي ، وليس لدينا كلمة مرور لتعيين PRNG (من الأفضل استخدام بذور مختلفة تعرف أيضًا بحالة المولد المعروفة باسم كلمات المرور للعمل مع ترميز RandomLSB و ± 1). الجواب بسيط قدر الإمكان. نحصل على الرسالة بنفس الطريقة التي حصلنا عليها بدون ترميز ± 1. قد لا نعرف حتى عن استخدامه. أكرر ، نستخدم هذه الحيلة فقط لتجاوز أدوات الكشف التلقائي . عند تضمين / استرداد رسالة ، نحن نعمل فقط مع LSB الخاص بها وليس أكثر. ومع ذلك ، عند الكشف ، نحتاج إلى مراعاة سياق التنفيذ ، أي كل بايتات الصورة ، من أجل بناء تقديرات إحصائية. هذا هو بالضبط النجاح الكامل لبرمجة ± 1.

بدلا من الاستنتاج

تم إجراء محاولة أخرى جيدة جدًا لاستخدام الإحصاءات ضد إخفاء معلومات LSB في طريقة تسمى أزواج العينة. يمكنك العثور عليها هنا. وجوده هنا سيجعل المقالة أكاديمية للغاية ، لذلك أتركها مهتمة بالقراءة اللامنهجية. ولكن توقعًا لأسئلة الجمهور ، سأجيب على الفور: لا ، لم يلتقط الترميز ± 1.

وبالطبع التعلم الآلي. الأساليب الحديثة القائمة على ML تعطي نتائج جيدة للغاية. يمكنك أن تقرأ عنها هنا وهنا .

بناءً على هذه المقالة ، تم كتابة أداة صغيرة (في الوقت الحالي). يمكنه توليد البيانات وتنفيذ هجوم مرئي بشكل منفصل على القنوات وحساب تقييم RS- و SPA وتصور نتائج Chi-square. ولن تتوقف عند هذا الحد.

للتلخيص ، أريد أن أعطي بعض النصائح:

• تضمين الرسالة في وحدات البايت العشوائية.
• قلل قدر المعلومات المضمنة قدر الإمكان (تذكر العم هامينج).
• استخدم ترميز ± 1.
• اختر الصور مع LSB صاخبة.
• تحديث Remdalp : استخدم الصور التي لا تظهر في أي مكان.
• كن لطيفا!

يسعدني أن أرى اقتراحاتك وإضافاتك وتصحيحاتك وملاحظاتك الأخرى!

PS أريد أن أعرب عن شكر خاص ل PavelMSTU للاستشارات والركلات التحفيزية.