بعد اكتشاف ثغرة في التجربة الشهيرة ، والتي أثبتت عدم وجود خصائص داخلية للأشياء الكمومية ، أغلقتها ثلاث مجموعات من المجربين بسرعة. تغلق هذه الحلقة قضية نظريات المتغيرات المخفية.
استخدم الفيزيائي النظري
جون ويلر ذات مرة عبارة "التنين المدخن الضخم" لوصف جسيم الضوء المتطاير من المصدر إلى عداد الفوتون. "فم التنين حاد حيث يعض المنضدة. وكتب ويلر أن ذيل التنين حاد من حيث يأتي الفوتون. بعبارة أخرى ، للفوتون حقيقة معينة في بداية ونهاية المسار. لكن حالته في الوسط - جسد التنين - ضبابية. "ليس لدينا الحق في التحدث عما يفعله التنين ، أو كيف يبدو بينهما."
دعم ويلر وجهة النظر القائلة بأن الظواهر الكمومية الأولية لا يمكن أن تسمى حقيقية حتى نقوم بملاحظة - وهو موقف فلسفي يسمى
مناهضة الواقعية . حتى أنه توصل إلى تجربة توضح أنه إذا كنت تصر على الواقعية - حيث يكون للأجسام الكمومية مثل الفوتونات دائمًا خصائص داخلية معينة ، والتي تشبه إلى حد كبير وجهة النظر الكلاسيكية للواقع - فعليك أن تقبل أن المستقبل يمكن أن يؤثر إلى الماضي. بسبب سخافة السفر عبر الزمن ،
دعت تجربة ويلر إلى مناهضة الواقعية على المستوى الكمي.
ولكن في مايو 2018 ، وجد رافائيل شافيز مع زملاء من المعهد الدولي للفيزياء ثغرة. أظهروا أن تجربة ويلر ، تحت افتراضات معينة ، يمكن تفسيرها باستخدام النموذج الكلاسيكي ، الذي ينسب الخصائص الداخلية للفوتون. زودوا التنين بجسد محدد بوضوح ، مخفي عن الشكلية الرياضية لميكانيكا الكم القياسية.
رافائيل شافيزاقترح فريق شافيز تعديل تجربة ويلر لاختبار الثغرات. سارعت ثلاث فرق أخرى مع خفة الحركة غير المعتادة لإجراء تجربة معدلة. أظهرت نتائجهم ، التي نُشرت في يونيو ، أن النماذج الكلاسيكية التي تعزز الواقعية لا تقدم تفسيرًا ذا معنى للنتائج. قد تكون ميكانيكا الكم غريبة ، لكنها تظل أبسط تفسير متاح.
فخ التنين
جاء ويلر بتجربته في عام 1983 للتأكيد على أحد الألغاز المفاهيمية الرئيسية لميكانيكا الكم:
ازدواجية الجسيمات الموجية . تتصرف الأجسام الكمومية إما كجزيئات أو كموجات ، ولكن ليس في نفس الوقت وهكذا. من هذه الخاصية لميكانيكا الكم ، يبدو أنه يتبع أن الأجسام ليس لها واقع داخلي حتى يتم ملاحظتها. قال
ديفيد كايزر ، الفيزيائي ومؤرخ العلوم في معهد ماساتشوستس للتكنولوجيا: "كان على الفيزيائيين تحمل الثنائية كميزة متأصلة وغريبة في نظرية الكم لما يقرب من مائة عام". "جاءت هذه الفكرة قبل السمات الغريبة النموذجية الأخرى لنظرية الكم ، مثل
مبدأ عدم اليقين هايزنبرغ وقطة شرودنغر ."
يتم التأكيد على هذه الظاهرة من خلال حالة خاصة من التجربة الشهيرة مع شقين يسمى
مقياس التداخل Mach - Zehnder .
في تجربة ، يتم إطلاق فوتون واحد نحو مرآة شفافة ، أو مقسم شعاع. الفوتون ذو الاحتمال المتساوي إما يعكسه أو يمر من خلاله - ونتيجة لذلك فإنه يتبع في النهاية أحد مسارين. في هذه الحالة ، سيذهب إما على طول المسار 1 ، أو على طول المسار 2 ، وسيكون إما في الكاشف D1 أو في D2 ، باحتمال متساوٍ. يتصرف الفوتون ككل غير مرئي ، مما يدل على طبيعته الجسدية.
ولكن هناك فارق بسيط. عند تقاطع المسارين 1 و 2 ، يمكنك إضافة فاصل شعاع آخر يغير كل شيء. في هذه الحالة ، تقول ميكانيكا الكم أن الفوتون ، كما هو ، يمر عبر مسارين في وقت واحد كموجة. تتقارب هاتان الموجتان معًا على فاصل شعاع ثان. يمكن إعداد التجربة بحيث يتم دمج الموجات بشكل بنّاء - من الذروة إلى الذروة ، والفشل في الفشل - فقط إذا اتجهت نحو كاشف D1. ويشير المسار إلى العداد D2 إلى تداخل مدمر. في هذه الحالة ، يمكن دائمًا العثور على الفوتون في D1 ، وليس أبدًا في D2. في هذه الحالة ، يوضح الفوتون طبيعته الموجية.
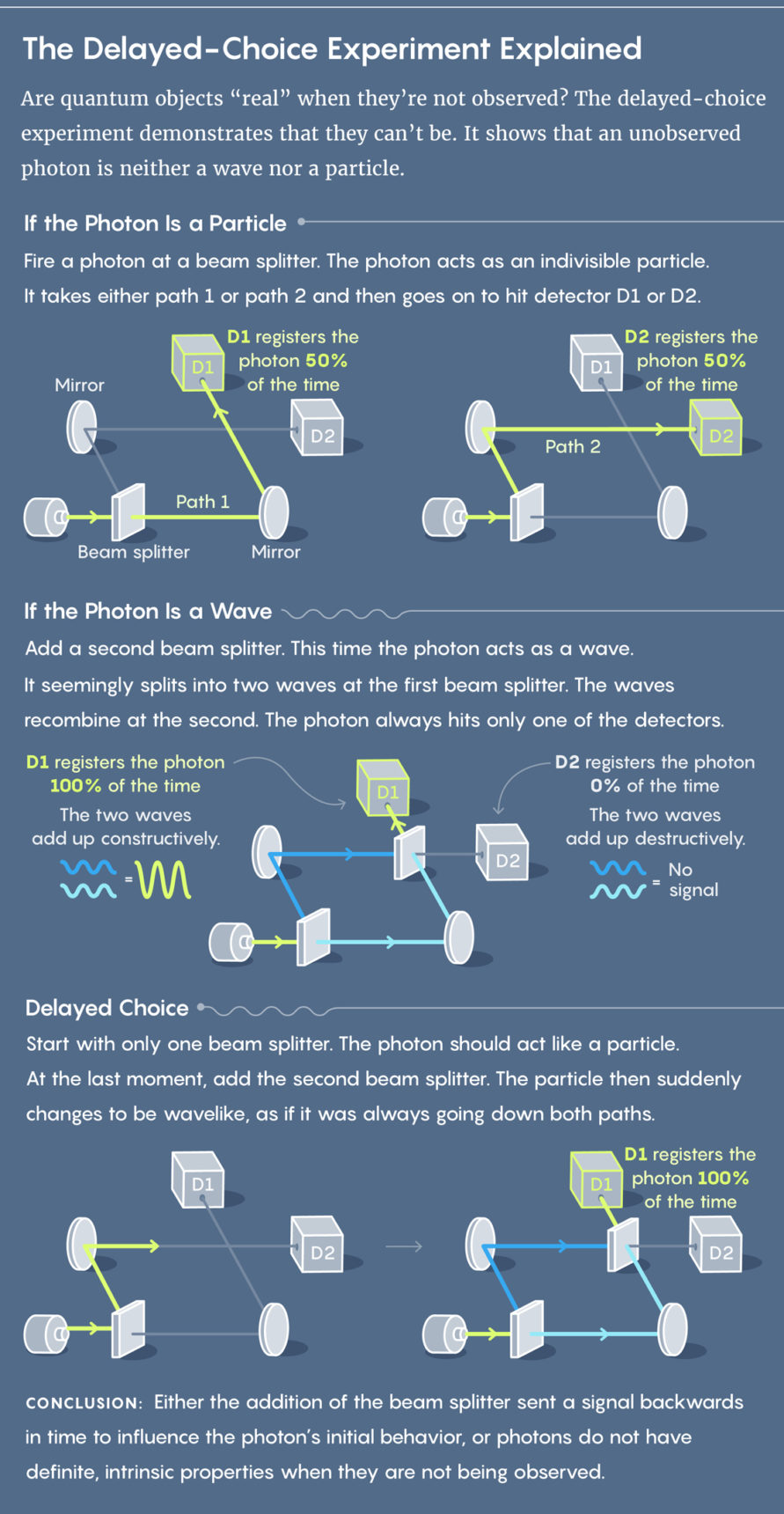أعلاه: الفوتون كجسيم. يقوم كل كاشف بتسجيل الفوتون في 50٪ من الحالات.
في الوسط: الفوتون مثل الموجة. يسجل الفوتون D1 فقط.
أدناه: الاختيار المعلق. نبدأ بدون مقسم شعاع ثان ، ونضيفه في اللحظة الأخيرة. يبدأ الفوتون ، الذي تصرف أولاً كجسيم ، فجأة في التصرف مثل الموجة.
الخلاصة: إما أن إدخال مقسم الشعاع الثاني يرسل إشارة إلى الفوتون في الماضي ، أو أن الفوتون ليس له خصائص داخلية.تجلى عبقرية ويلر في السؤال: ماذا لو تأخرنا في اختيار ما إذا كان يجب إضافة مقسم شعاع ثانٍ؟ افترض أن الفوتون يدخل في مقياس التداخل عندما لا يكون هناك مقسم شعاع ثان. يجب أن تتصرف مثل الجسيمات. ولكن يمكنك إضافة مقسم شعاع ثان في نانو ثانية الأخيرة. توضح النظرية والتجربة أن الفوتون ، الذي كان عليه في السابق أن يتصرف مثل الجسيم ، ويدخل إما في الكاشف D1 أو إلى D2 ، يبدأ في التصرف مثل الموجة ، ويدخل فقط في D1. للقيام بذلك ، يبدو أنه بحاجة إلى السير في مسارين في وقت واحد ، وليس على أحدهما. بالمعنى الكلاسيكي ، يحدث كل شيء كما لو أن الفوتون عاد في الوقت المناسب وغير جوهره من الجسيم إلى الموجة.
تتمثل إحدى طرق تجنب مثل هذه العلاقة السببية [تأثير الأحداث من المستقبل على الماضي] في إنكار الفوتون على حقيقة داخلية والإشارة إلى أن الفوتون يصبح حقيقيًا فقط عند قياسه. ثم ليس لدينا ما نتراجع عنه.
تلقت هذه المعاداة للواقعية ، التي ترتبط غالبًا
بتفسير كوبنهاغن لميكانيكا الكم ، ضربة نظرية بعد نشر عمل شافيز ، على الأقل في سياق هذه التجربة. قرر فريقه شرح الخصائص غير البديهية لميكانيكا الكم بمجموعة جديدة من الأفكار ، والنمذجة [السببية] ، التي نمت شعبيتها في العقد الماضي بمساعدة عالم الكمبيوتر
جود بيرل وآخرين. تحدد النمذجة السببية العلاقة السببية بين مختلف عناصر التجربة. في كثير من الأحيان ، عند دراسة الأحداث المترابطة - دعنا نسميها A و B - لا يمكننا بالتأكيد أن نقول أن A هو سبب B ، أو أن B هو سبب A ، هناك احتمال أن يكون سبب كل منهما هو الحدث غير المتوقع أو "المخفي" B. في مثل هذه الحالات ، قد تساعد النمذجة السببية في الكشف عن هذا B.
ركز شافيز وزملاؤه ،
غابرييلا ليموس وجاك بينارد ، على تجربة ويلر المتأخرة ، متوقعين الفشل في العثور على نموذج مع عملية خفية من شأنها أن تمنح الفوتون حقيقة داخلية وتشرح سلوكه دون أي عواقب. وقال شافيز إنهم يعتقدون أنهم سيثبتون أن تجربة الاختيار المؤجل كانت "غير بديهية للغاية ، بمعنى أنه لا يمكن لأي نموذج سببي أن يفسر ذلك".
غابرييلا ليموسلكن المفاجأة كانت تنتظرهم. كانت المهمة بسيطة للغاية. بدأوا باقتراح أن الفوتون ، مباشرة بعد مروره عبر مقسم الشعاع الأول ، لديه حالة داخلية محددة بـ "متغير مخفي". في هذا السياق ، المتغير المخفي هو شيء غير متوفر في ميكانيكا الكم القياسية ، ولكنه يؤثر بطريقة ما على سلوك الفوتون. ثم قرر المجرب إضافة أو إزالة مقسم شعاع ثان. تضمن النمذجة السببية التي تحظر السفر إلى الماضي ألا يؤثر اختيار المجرب على الحالة السابقة للفوتون.
بالنظر إلى متغير مخفي يدعم الواقعية ، أظهر الفريق أنه من الممكن كتابة القواعد التي تستخدم قيمة المتغير ووجود أو عدم وجود مقسم شعاع ثان لإجراء الفوتون إلى D1 أو D2 بطريقة تكرر توقعات ميكانيكا الكم. لقد حصلوا على تفسير كلاسيكي ، سببي وواقعي. وجدوا ثغرة جديدة.
قال
تيم بيرنز ، المتخصص في الفيزياء النظرية الكمومية من جامعة نيويورك في شنغهاي ، أن هذا فاجأ العديد من الفيزيائيين. قال بيرنز: "ما لم يقدره الناس هو أن هذا النوع من التجارب يسمح بتفسير كلاسيكي يكرر نتائج التجربة بشكل مثالي". "يمكنك إنشاء نظرية بمتغير مخفي ، بدون أي ميكانيكا كمية."
قال شافيز "لقد كانت خطوة صفرية". الخطوة التالية هي معرفة كيفية تعديل تجربة ويلر بحيث يمكن التمييز بين النظرية الكلاسيكية للمتغيرات المخفية وميكانيكا الكم.
في التجربة المعدلة ، ظل مقياس التداخل Mach - Zehnder دون تغيير ؛ يوجد دائمًا مقسم شعاع. بدلاً من ذلك ، يتم لعب دور التعديلات التجريبية ، التي يمكن للباحث تغييرها حسب الرغبة ، من خلال نوبات مرحلتين - واحدة في بداية التجربة ، والأخرى في النهاية.
يغير التأثير المشترك لتحولات الطورين الطول النسبي للمسار. هذا يغير صورة التداخل ، ومعها الموجة المفترضة أو سلوك الجسيمات للفوتون. على سبيل المثال ، يمكن أن تكون قيمة تحول الطور الأول بحيث يتصرف الفوتون مثل جسيم داخل مقياس التداخل ، ويمكن أن يتسبب التحول الثاني في سلوكه مثل الموجة. احتاج الباحثون إلى التحول الثاني للضبط بعد الأول.
مع هذا الإعداد التجريبي ، توصل فريق تشافيز إلى طريقة للتمييز بين النموذج السببي الكلاسيكي وميكانيكا الكم. لنفترض أن المرحلة الأولى من التحول يمكن أن تأخذ أحد المتغيرات الثلاثة ، والثانية من اثنين. اتضح ستة إعدادات ممكنة للتجربة. وهنا تختلف تنبؤات النموذج الكلاسيكي للمتغيرات المخفية وميكانيكا الكم القياسية. ثم صنع العلماء صيغة. تتلقى الصيغة عند مدخلاتها الاحتمالات المحسوبة على أساس عدد المرات التي يصل فيها الفوتون إلى كاشف معين (بناءً على صياغة ذات مرحلتين من التحولات). إذا كانت الصيغة صفرًا ، فإن النموذج السببي الكلاسيكي قادر على شرح الإحصائيات. ولكن إذا أعطت المعادلة رقمًا أكبر من الصفر ، فبسبب قيود معينة مفروضة على المتغيرات المخفية ، لا يوجد تفسير كلاسيكي للنتائج التجريبية.
تعاون تشافيز مع فابيو سكيارينو ، المتخصص في فيزياء الكم من جامعة سابينزا في روما ، وزملائه لاختبار عدم المساواة. في الوقت نفسه ، قام فريقان صينيان - أحدهما بقيادة جان وي بان ، فيزيائي تجريبي من جامعة خفي للعلوم والتكنولوجيا ، والثاني بقيادة غوانغ كانغ قوه ، من نفس الجامعة - بإجراء تجاربهم.
نفذ كل فريق المخطط بشكل مختلف قليلاً. التزمت مجموعة Guo بخيار بسيط باستخدام مقياس تداخل Mach-Zehnder حقيقي. قال هوارد وايزمان ، الفيزيائي النظري في جامعة جريفيث الذي لم يشارك في التجارب: "هذه التجربة ، في رأيي ، هي الأقرب إلى اقتراح ويلر الأصلي".
أظهرت جميع الفرق الثلاثة أن نتيجة حساب الصيغة تتجاوز الصفر مع دلالة إحصائية لا يمكن دحضها. لقد استبعدوا تلك النماذج السببية الكلاسيكية التي يمكن أن تفسر تجربة ويلر مع خيار مؤجل. تم إغلاق الثغرة. قال بان "تجربتنا أنقذت تجربة فكر ويلر الشهيرة".
تلك المتغيرات الخفية التي لا تزال قائمة
أعجب كايزر بالعمل النظري "الأنيق" لشافيز والتجارب اللاحقة. "إن حقيقة وجود علامات واضحة على عدم المساواة في كل تجربة هي دليل مقنع على أن النماذج" الكلاسيكية "لمثل هذه الأنظمة لا تصف في الواقع المخطط الحقيقي لعمل العالم ، بينما تتطابق التوقعات الميكانيكية الكمومية تمامًا مع أحدث النتائج" قال.
يتم استخدام الصيغة مع افتراضات معينة. واحدة من أكبر المتغيرات المخفية الكلاسيكية المستخدمة في النموذج السببي ، يمكن أن تأخذ واحدة من قيمتين ، مشفرة في جزء واحد من المعلومات. يعتبر شافيز هذا معقولًا ، لأن النظام الكمي - الفوتون - يمكنه أيضًا ترميز جزء واحد فقط من المعلومات (يذهب إما في ذراع واحد من مقياس التداخل أو في الآخر). قال شافيز: "سيكون من الطبيعي أن نذكر أن نموذج المتغيرات الخفية يجب أن يكون ثنائي الأبعاد".
ديفيد قيصرلكن المتغير الخفي مع القدرة الإضافية على حمل المعلومات يمكن أن يعيد قدرة النموذج السببي على تفسير الإحصائيات التي تمت ملاحظتها في تجربة معدلة مع اختيار متأخر.
علاوة على ذلك ، فإن هذه التجارب لا تدحض نظرية المتغيرات الخفية الأكثر شيوعًا.
إن نظرية de Broglie-Bohm ، وهي بديل حاسم وواقعي لميكانيكا الكم القياسية ، قادرة على شرح تجربة مع خيار مؤجل. وفقًا لهذه النظرية ، تحتوي الجسيمات دائمًا على موقع (وهي متغيرات مخفية) ، وبالتالي ، الواقع الموضوعي ، ولكن في نفس الوقت يتم توجيهها بموجة. لذلك ، فإن الواقع هو الموجة والجذر. تنتقل الموجة على كلا المسارين ، والجسيم ينتقل على طول أحد المسارين. يؤثر وجود أو عدم وجود مقسم شعاع ثان على الموجة التي توصل الجسيم إلى أجهزة الكشف - وتتزامن هذه النتيجة مع ميكانيكا الكم القياسية.
بالنسبة إلى وايزمان ، فإن النقاش حول المواجهة بين تفسير كوبنهاجن ونظرية دي بروجلي بوم ليست بعيدة عن الاكتمال. وكتب في رسالة بالبريد الإلكتروني "في تفسير كوبنهاجن لا يوجد تداول غريب للوقت على وجه التحديد لأنه ليس لدينا الحق في الحديث عن ماض الفوتون". في تفسير de Broglie-Bohm ، هناك واقع مستقل عن معرفتنا ، ولكن لا توجد مشكلة ، حيث لا يوجد انعكاس زمني - ولكن هناك وصف سببي فريد (تطلعي) ".
كايزر ، يشيد بالمحاولات التي قام بها ، يريد المضي قدمًا. في التجارب الحالية ، تم اختيار ما إذا كان سيتم إضافة تحول المرحلة الثانية أو مقسم الحزمة الثاني أم لا بواسطة مولد رقم عشوائي الكم. ولكن في هذه التجربة ، يتم اختبار ميكانيكا الكم نفسها ، والتي لها مذاق لاحق من الاعتماد الدائري. وقال قيصر: "سيكون من الجميل التحقق مما إذا كانت النتائج التجريبية ستظل متسقة حتى مع التصاميم القائمة على مصادر عشوائية مختلفة تمامًا".
تحقيقا لهذه الغاية ، ابتكر كايزر وزملاؤه مصدرًا عشوائيًا باستخدام الفوتونات القادمة من الكوازارات البعيدة ، والتي اجتاز الكثير منها أكثر من نصف الكون [الملحوظ]. تم جمع الفوتونات بواسطة التلسكوب الذي يبلغ ارتفاعه مترًا
في مرصد جبل الطاولة في كاليفورنيا. إذا كان طول موجة الفوتون لا يتجاوز عتبة معينة ، فإن مولد الأرقام العشوائية يعطي 0 ، وإلا 1. من حيث المبدأ ، يمكن استخدام هذا البت لاختيار الظروف التجريبية بشكل عشوائي. وقال كايزر ، إذا استمرت النتائج في دعم البيان الأولي لـ Wheeler ، فإن "هذا سيعطينا سببًا آخر للقول بأن ازدواجية موجة الموجة لا يمكن تفسيرها في الفيزياء الكلاسيكية". - انخفض نطاق البدائل المفاهيمية لفيزياء الكم مرة أخرى ، وقد تم بالفعل محاصرته. وهذا هو بالضبط ما نسعى إليه ".
في هذه الأثناء ، أصبح جسم التنين ، الذي ظهر في مرمى البصر لبضعة أسابيع قصيرة ، مدخنًا وغامضًا مرة أخرى.
يمكن العثور على المزيد من المقالات حول موضوع العلوم الشعبية في golovanov.net . اشترك في التحديثات عن طريق البريد الإلكتروني أو RSS . يتم نسخ المقالات أيضًا على قناة Yandex.Zen .