🛡️ 👩🏿‍🤝‍👨🏽 👌🏻 مقدمة بسيطة لـ ALU للشبكات العصبية: الشرح والمعنى المادي والتنفيذ 🙅🏿 💚 🏈

في الآونة الأخيرة ، نشر الباحثون في Google DeepMind ، بما في ذلك عالم الذكاء الاصطناعي الشهير ، مؤلف كتاب " فهم التعلم العميق " ، أندرو تراسك ، مقالة مثيرة للإعجاب تصف نموذج الشبكة العصبية لاستقراء قيم الوظائف العددية البسيطة والمعقدة بدرجة عالية من الدقة.

في هذا المنشور سأشرح بنية NALU ( الأجهزة المنطقية الحسابية العصبية ، NALU) ومكوناتها والاختلافات الكبيرة عن الشبكات العصبية التقليدية. الهدف الرئيسي من هذه المقالة هو شرح NALU (التنفيذ والفكرة) للعلماء والمبرمجين والطلاب الجدد على الشبكات العصبية والتعلم العميق.

ملاحظة من المؤلف : أوصي بشدة بقراءة المقال الأصلي للحصول على دراسة أكثر تفصيلاً للموضوع.

متى تكون الشبكات العصبية خاطئة؟

صورة مأخوذة من هذه المقالة.

نظريًا ، يجب أن تقارب الشبكات العصبية الوظائف جيدًا. إنهم قادرون دائمًا على تحديد المراسلات الهامة بين بيانات الإدخال (العوامل أو الميزات) والمخرجات (التسميات أو الأهداف). هذا هو السبب في استخدام الشبكات العصبية في العديد من المجالات ، من التعرف على الأشياء وتصنيفها إلى ترجمة الكلام إلى نص وتنفيذ خوارزميات اللعبة التي يمكن أن تهزم أبطال العالم. تم إنشاء العديد من النماذج المختلفة بالفعل: الشبكات العصبية التلافيفية والمتكررة ، وأجهزة الترميز ، وما إلى ذلك. النجاح في إنشاء نماذج جديدة للشبكات العصبية والتعلم العميق هو موضوع كبير بحد ذاته.

ومع ذلك ، وفقًا لمؤلفي المقالة ، لا تتعامل الشبكات العصبية دائمًا مع المهام التي تبدو واضحة للناس وحتى النحل ! على سبيل المثال ، هذا حساب شفهي أو عمليات بأرقام ، بالإضافة إلى القدرة على تحديد التبعية من العلاقات. أظهر المقال أن النماذج القياسية للشبكات العصبية لا يمكنها حتى التعامل مع الخرائط المتطابقة (وهي وظيفة تترجم الحجة إلى نفسها ،

f (x) = x

$f (x) = x$ ) هي العلاقة العددية الأكثر وضوحا. يوضح الشكل أدناه MSE لنماذج مختلفة من الشبكات العصبية عند التعلم على قيم هذه الوظيفة.

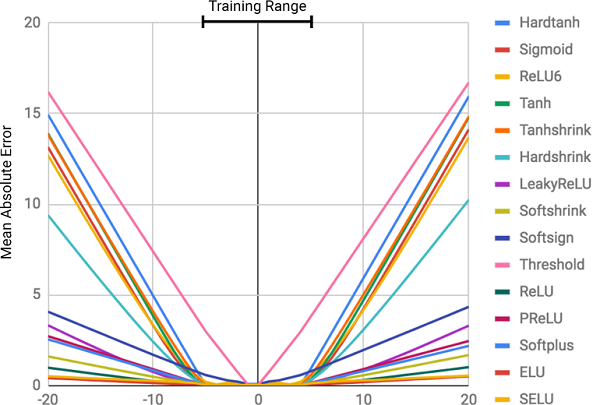يعني الخطأ التربيعي للشبكات العصبية القياسية

يعني الخطأ التربيعي للشبكات العصبية القياسية

يوضح الشكل متوسط الخطأ المربع للشبكات العصبية القياسية التي تستخدم نفس البنية ووظائف التنشيط المختلفة (غير الخطية) في الطبقات الداخلية

لماذا الشبكات العصبية خاطئة؟

كما يتبين من الشكل ، فإن السبب الرئيسي للخطوات هو عدم خطية وظائف التنشيط على الطبقات الداخلية للشبكة العصبية. يعمل هذا النهج بشكل رائع لتحديد العلاقات غير الخطية بين بيانات الإدخال والاستجابات ، ولكن من الخطأ الفادح تجاوز البيانات التي تعلمتها الشبكة. وبالتالي ، تقوم الشبكات العصبية بعمل ممتاز لتذكر الاعتماد العددي من بيانات التدريب ، لكنها لا تستطيع استقراء ذلك.

يشبه ذلك حصر الإجابة أو الموضوع قبل الاختبار دون فهم الموضوع. من السهل اجتياز الاختبار إذا كانت الأسئلة مشابهة للواجب المنزلي ، ولكن إذا كان فهم الموضوع قيد الاختبار ، وليس القدرة على التذكر ، فسوف نفشل.

هاري بوتر

لم يكن هذا في برنامج الدورة!

ترتبط درجة الخطأ مباشرة بمستوى عدم الخطية لوظيفة التنشيط المختارة. يوضح الرسم البياني السابق بوضوح أن الوظائف غير الخطية ذات القيود الصارمة ، مثل السيني أو المماس الزائدي ( Tanh ) ، يمكن أن تتعامل مع مهمة تعميم التبعيات أسوأ بكثير من الوظائف المقيدة لينة ، مثل التحول الخطي المبتور ( ELU ، PReLU ).

الحل: البطارية العصبية (NAC)

توجد البطارية العصبية ( NAC ) في قلب طراز NALU . هذا جزء بسيط ولكنه فعال من شبكة عصبية تتعامل مع الجمع والطرح ، وهو أمر ضروري لحساب العلاقات الخطية بكفاءة.

NAC هي طبقة خطية خاصة لشبكة عصبية ، يتم فرض شرط بسيط على وزنها: يمكن أن تأخذ 3 قيم فقط - 1 أو 0 أو -1 . لا تسمح هذه القيود للبطارية بتغيير نطاق بيانات الإدخال ، وتظل ثابتة على جميع طبقات الشبكة ، بغض النظر عن عددها واتصالاتها. وبالتالي ، فإن الناتج هو مزيج خطي من قيم متجه الإدخال ، والذي يمكن أن يكون بسهولة عملية الجمع والطرح.

أفكار بصوت عال : لفهم أفضل لهذه العبارة ، دعنا نلقي نظرة على مثال لبناء طبقات من شبكة عصبية تؤدي عمليات حسابية خطية على بيانات الإدخال.

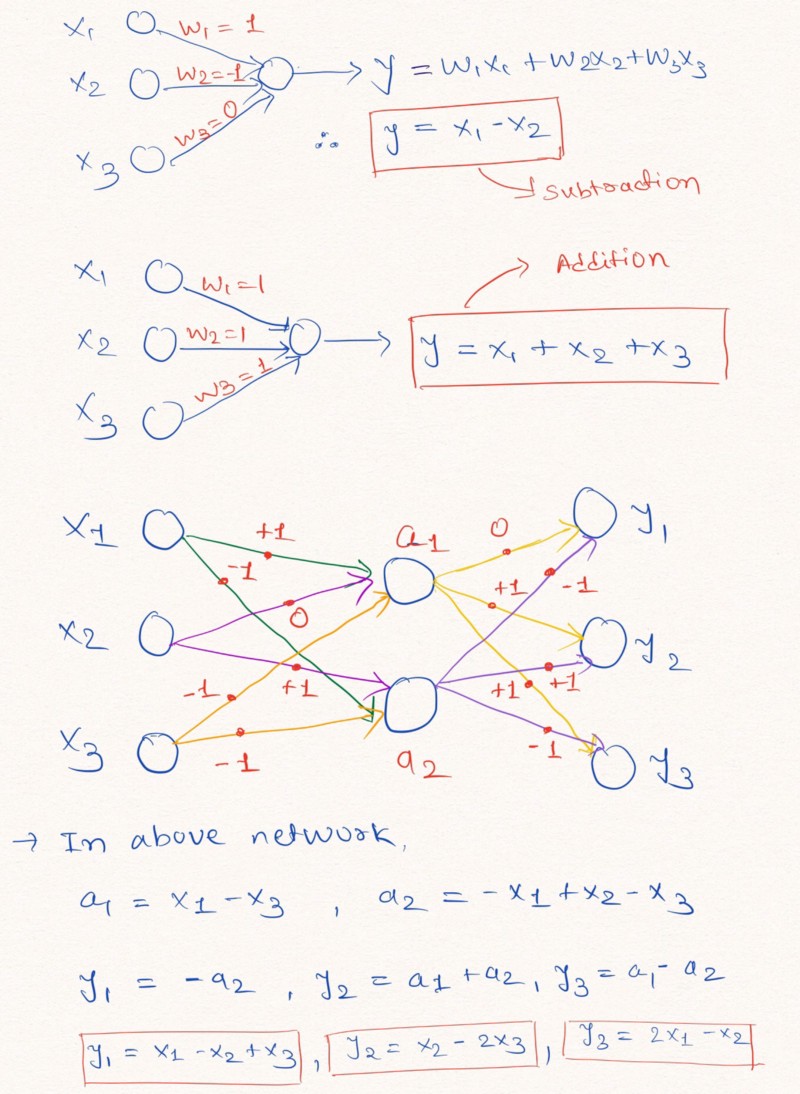الاستقراء الخطي في الشبكة العصبية

يوضح الشكل كيف يمكن لطبقات الشبكة العصبية دون إضافة ثابت ومع القيم المحتملة للأوزان -1 أو 0 أو 1 ، القيام باستقراء خطي

كما هو موضح أعلاه في صورة الطبقات ، يمكن للشبكة العصبية أن تتعلم استقراء قيم وظائف الحساب البسيطة مثل الجمع والطرح (

y = x_{1} + x_{2}

$y = x_1 + x_2$ و

y = x_{1} - x_{2}

$y = x_1 - x_2$ ) ، باستخدام قيود الأوزان مع القيم المحتملة 1 و 0 و -1.

ملاحظة: لا تحتوي طبقة NAC في هذه الحالة على مصطلح حر (ثابت) ولا تطبق تحويلات غير خطية على البيانات.

نظرًا لأن الشبكات العصبية القياسية لا يمكنها التعامل مع حل المشكلة في ظل قيود مماثلة ، فإن مؤلفي المقالة يقدمون صيغة مفيدة جدًا لحساب هذه المعلمات من خلال المعلمات الكلاسيكية (غير المحدودة)

h a t W

$\ hat {W}$ و

h a t M

$\ hat {M}$ . يمكن تهيئة بيانات الوزن ، مثل جميع معلمات الشبكات العصبية ، بشكل عشوائي واختيارها في عملية تدريب الشبكة. صيغة لحساب المتجه

W

$W$ من خلال

h a t W

$\ hat {W}$ و

h a t M

$\ hat {M}$ يبدو مثل هذا:

W = t a n h (h a t W) o d o t s i g m a (h a t M)

$W = tanh (\ hat {W}) \ odot \ sigma (\ hat {M})$

تستخدم الصيغة منتج مصفوفة عنصري

يضمن استخدام هذه الصيغة أن نطاق قيم W يقتصر على الفاصل الزمني [-1 ، 1] ، الأقرب إلى المجموعة -1 ، 0 ، 1. أيضًا ، تختلف الوظائف من هذه المعادلة بمعلمات الوزن. وبالتالي ، سيكون من الأسهل على طبقة NAC أن تتعلم القيم

W

$W$ باستخدام هبوط التدرج والانتشار الخلفي للخطأ . فيما يلي رسم تخطيطي لهندسة طبقة NAC .

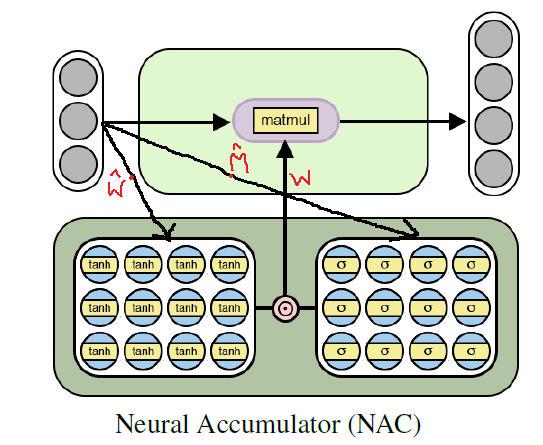بنية البطارية العصبية للتدريب على الوظائف الحسابية الأولية (الخطية)

تنفيذ Python NAC باستخدام Tensorflow

كما فهمنا بالفعل ، NAC هي شبكة عصبية بسيطة إلى حد ما (طبقة شبكة) ذات ميزات صغيرة. فيما يلي تنفيذ لطبقة NAC واحدة في Python باستخدام مكتبات Tensoflow و NumPy.

كود بايثون

import numpy as np import tensorflow as tf #    (NAC)  / # ->     / def nac_simple_single_layer(x_in, out_units): '''  : x_in ->   X out_units ->     : y_out ->     W ->     ''' #       in_features = x_in.shape[1] #  W_hat  M_hat W_hat = tf.get_variable(shape=[in_shape, out_units], initializer=tf.initializers.random_uniform(minval=-2, maxval=2), trainable=True, name='W_hat') M_hat = tf.get_variable(shape=[in_shape, out_units], initializer=tf.initializers.random_uniform(minval=-2, maxval=2), trainable=True, name='M_hat') #  W   W = tf.nn.tanh(W_hat) * tf.nn.sigmoid(M_hat) y_out = tf.matmul(x_in, W) return y_out, W

في الكود أعلاه

h a t W

$\ hat {W}$ و

h a t M

$\ hat {M}$ تتم تهيئتها باستخدام توزيع موحد ، ولكن يمكنك استخدام أي طريقة موصى بها لتوليد تقريب أولي لهذه المعلمات. يمكنك مشاهدة النسخة الكاملة من الشفرة في مستودع GitHub الخاص بي (الرابط مكرر في نهاية المنشور).

الانتقال: من الجمع والطرح إلى NAC للتعبيرات الحسابية المعقدة

على الرغم من أن نموذج الشبكة العصبية البسيطة الموصوفة أعلاه يتواءم مع أبسط العمليات مثل الجمع والطرح ، فإننا بحاجة إلى أن نكون قادرين على التعلم من المعاني المتعددة للوظائف الأكثر تعقيدًا ، مثل الضرب والقسمة والأسي.

أدناه هي بنية NAC المعدلة ، والتي تم تكييفها لاختيار العمليات الحسابية الأكثر تعقيدًا من خلال اللوغاريتم وأخذ الأس داخل النموذج. لاحظ الاختلافات بين تنفيذ NAC هذا والذي تمت مناقشته بالفعل أعلاه.

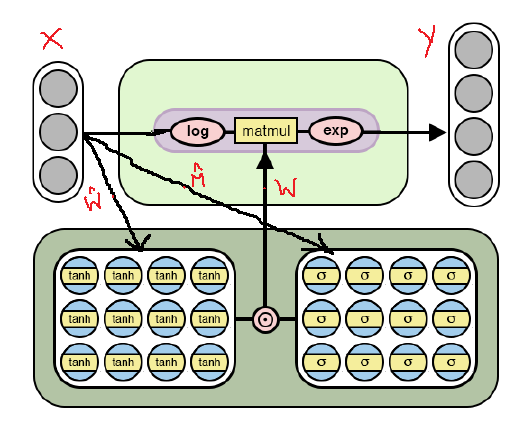الصورة

بنية NAC لعمليات حسابية أكثر تعقيدًا

كما يتبين من الشكل ، فإننا نقوم بتسجيل لوغاريتمات بيانات الإدخال قبل الضرب في مصفوفة الأوزان ، ثم نحسب الأس للنتيجة. صيغة الحسابات هي كما يلي:

Y = e x p (W b u l l e t (l o g (| x | + e p s i l o n)))

$Y = exp (W \ bullet (log (| x | + \ epsilon)))$

صيغة الإخراج للنسخة الثانية من NAC .

$\ epsilon$ هنا رقم صغير جدًا لمنع حالات مثل log (0) أثناء التدريب

وبالتالي ، بالنسبة لكلا طرازين NAC ، فإن مبدأ التشغيل ، بما في ذلك حساب مصفوفة الوزن مع القيود

W

$W$ من خلال

h a t W

$\ hat {W}$ و

h a t M

$\ hat {M}$ لا يتغير. والفرق الوحيد هو استخدام العمليات اللوغاريتمية على المدخلات والمخرجات في الحالة الثانية.

إصدار NAC الثاني في Python باستخدام Tensorflow

بالكاد سيتغير الرمز ، مثل الهندسة المعمارية ، باستثناء التحسينات المشار إليها في حساب موتر قيم الإخراج.

كود بايثون

 #    (NAC)     # ->      ,   ,      def nac_complex_single_layer(x_in, out_units, epsilon=0.000001): ''' :param x_in:   X :param out_units:    :param epsilon:    (,    log(0)   ) :return m:     :return W:     ''' in_features = x_in.shape[1] W_hat = tf.get_variable(shape=[in_shape, out_units], initializer=tf.initializers.random_uniform(minval=-2, maxval=2), trainable=True, name="W_hat") M_hat = tf.get_variable(shape=[in_shape, out_units], initializer=tf.initializers.random_uniform(minval=-2, maxval=2), trainable=True, name="M_hat") #  W   W = tf.nn.tanh(W_hat) * tf.nn.sigmoid(M_hat) #          x_modified = tf.log(tf.abs(x_in) + epsilon) m = tf.exp(tf.matmul(x_modified, W)) return m, W

أذكرك مرة أخرى أنه يمكن العثور على النسخة الكاملة من التعليمات البرمجية في مستودع GitHub الخاص بي (الرابط مكرر في نهاية المنشور).

تجميع كل شيء معًا: وحدة المنطق الحسابي العصبي (NALU)

كما خمّن الكثير بالفعل ، يمكننا أن نتعلم من أي عملية حسابية تقريبًا ، مع الجمع بين النموذجين اللذين تمت مناقشتهما أعلاه. هذه هي الفكرة الرئيسية لـ NALU ، والتي تتضمن مزيجًا مرجحًا من NAC الأولي والمعقد ، يتم التحكم فيه من خلال إشارة التدريب. وبالتالي ، فإن NACs هي اللبنات الأساسية لبناء NALUs ، وإذا فهمت تصميمها ، فسيكون بناء NALUs أمرًا سهلاً. إذا كانت لا تزال لديك أسئلة ، فحاول قراءة التفسيرات لكلا طرازي NAC مرة أخرى. فيما يلي رسم تخطيطي لهندسة NALU .

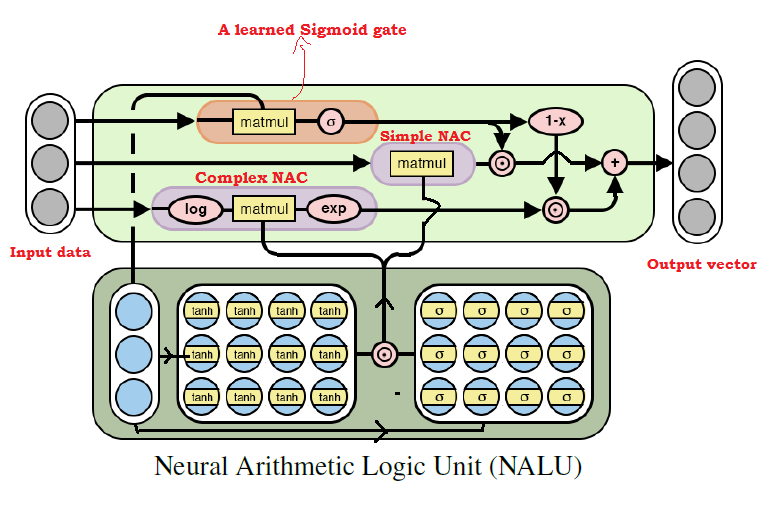الصورة

مخطط NALU مع تفسيرات

كما يتبين من الشكل أعلاه ، فإن كل من وحدات NAC (كتل أرجوانية) داخل NALU محرف (مدمجة) من خلال إشارة التدريب السينية (كتلة برتقالية). يتيح لك هذا (de) تنشيط إخراج أي منها ، اعتمادًا على الدالة الحسابية ، التي نحاول العثور على قيمها.

كما ذكر أعلاه ، فإن وحدة NAC الابتدائية هي وظيفة متراكمة ، تسمح لـ NALU بإجراء عمليات خطية أولية (الجمع والطرح) ، في حين أن وحدة NAC المعقدة مسؤولة عن الضرب والقسمة والأسي. يمكن تمثيل الإخراج في NALU كصيغة:

رمز زائف

 Simple NAC : a = WX Complex NAC: m = exp(W log(|X| + e))  W = tanh(W_hat) * sigmoid(M_hat) #  G -       : g = sigmoid(GX) # , ,   NALU #  *      NALU: y = g * a + (1 - g) * m

من صيغة NALU أعلاه ، يمكننا أن نستنتج ذلك بـ

g = 0

$g = 0$ ستختار الشبكة العصبية القيم فقط للعمليات الحسابية المعقدة ، ولكن ليس للعمليات الابتدائية ؛ والعكس صحيح - في حالة

g = 1

$g = 1$ . وبالتالي ، بشكل عام ، NALU قادرة على معرفة أي عملية حسابية تتكون من الجمع والطرح والضرب والقسمة والرفع إلى قوة واستقراء النتيجة بنجاح خارج حدود الفواصل الزمنية لقيم بيانات المصدر.

تنفيذ Python NALU باستخدام Tensorflow

في تنفيذ NALU ، سنستخدم NAC الأولي والمعقد ، الذي حددناه بالفعل.

كود بايثون

 def nalu(x_in, out_units, epsilon=0.000001, get_weights=False): ''' :param x_in:   X :param out_units:    :param epsilon:    (,    log(0)   ) :param get_weights:   True      :return y_out:     :return G: o   :return W_simple:    NAC1 ( NAC) :return W_complex:    NAC2 ( NAC) ''' in_features = x_in.shape[1] #     NAC a, W_simple = nac_simple_single_layer(x_in, out_units) #     NAC m, W_complex = nac_complex_single_layer(x_in, out_units, epsilon=epsilon) #    G = tf.get_variable(shape=[in_shape, out_units], initializer=tf.random_normal_initializer(stddev=1.0), trainable=True, name="Gate_weights") g = tf.nn.sigmoid(tf.matmul(x_in, G)) y_out = g * a + (1 - g) * m if(get_weights): return y_out, G, W_simple, W_complex else: return y_out

مرة أخرى ، ألاحظ أنه في الكود أعلاه ، قمت بتهيئة مصفوفة المعلمة مرة أخرى

G

$G$ باستخدام التوزيع الموحد ، ولكن يمكنك استخدام أي طريقة موصى بها لإنشاء تقريب أولي.

الملخص

بالنسبة لي شخصيًا ، تعد فكرة NALU تقدمًا كبيرًا في مجال الذكاء الاصطناعي ، خاصة في الشبكات العصبية ، وتبدو واعدة. يمكن أن يفتح هذا النهج الباب أمام مجالات التطبيق التي لا تستطيع الشبكات العصبية القياسية التعامل معها.

يتحدث مؤلفو المقالة عن تجارب مختلفة باستخدام NALU : من تحديد قيم وظائف الحساب الأولية إلى حساب عدد الأرقام المكتوبة بخط اليد في سلسلة معينة من صور MNIST ، والتي تسمح للشبكات العصبية بفحص برامج الكمبيوتر!

تعطي النتائج انطباعًا مذهلاً وتثبت أن NALU تتعامل مع أي مهام تقريبًا تتعلق بالتمثيل الرقمي ، أفضل من النماذج القياسية للشبكات العصبية. أنا أشجع القراء على التعرف على نتائج التجارب من أجل فهم أفضل لكيفية ومكان فائدة نموذج NALU .

ومع ذلك ، يجب أن نتذكر أنه لا NAC ولا NALU هما الحل المثالي لأي مهمة. بدلاً من ذلك ، يمثلون الفكرة العامة حول كيفية إنشاء نماذج لفئة معينة من العمليات الحسابية.

يوجد أدناه رابط إلى مستودع GitHub الخاص بي ، والذي يحتوي على التنفيذ الكامل للشفرة من المقالة.
github.com/faizan2786/nalu_implementation

يمكنك التحقق بشكل مستقل من تشغيل النموذج الخاص بي على وظائف مختلفة عن طريق تحديد معلمات عالية لشبكة عصبية. يرجى طرح الأسئلة ومشاركة أفكارك في التعليقات ضمن هذا المنشور ، وسأبذل قصارى جهدي للإجابة عليك.

ملاحظة (من المؤلف): هذه أول مشاركة لي مكتوبة على الإطلاق ، لذلك إذا كان لديك أي نصائح أو اقتراحات أو توصيات للمستقبل (سواء الفنية أو العامة) ، يرجى الكتابة لي.

PPS (من المترجم): إذا كان لديك تعليقات على الترجمة أو النص ، يرجى كتابة رسالة شخصية إلي. أنا مهتم بشكل خاص بصياغة إشارة البوابة المستفادة - لست متأكدًا من أنه يمكنني ترجمة هذا المصطلح بدقة.

مقدمة بسيطة لـ ALU للشبكات العصبية: الشرح والمعنى المادي والتنفيذ

متى تكون الشبكات العصبية خاطئة؟

لماذا الشبكات العصبية خاطئة؟

الحل: البطارية العصبية (NAC)

تنفيذ Python NAC باستخدام Tensorflow

الانتقال: من الجمع والطرح إلى NAC للتعبيرات الحسابية المعقدة

إصدار NAC الثاني في Python باستخدام Tensorflow

تجميع كل شيء معًا: وحدة المنطق الحسابي العصبي (NALU)

تنفيذ Python NALU باستخدام Tensorflow

الملخص

More articles: