إن مفهوم الحوسبة الكسولة لا يستحق الحديث عنه بالتفصيل. فكرة القيام بنفس الشيء في كثير من الأحيان ، خاصة إذا كانت طويلة وثقيلة ، قديمة قدم العالم. لأنه على الفور إلى هذه النقطة.
وفقًا لمؤلف هذا النص ، يجب على المُحسِّن العادي أن:
- حفظ الحسابات بين مكالمات البرنامج.
- تتبع التغييرات في شجرة الحساب.
- لديها بنية شفافة إلى حد ما.

المفهوم
من أجل:
- حفظ الحسابات بين مكالمات البرنامج:
في الواقع ، إذا قمنا باستدعاء نفس البرنامج النصي عدة عشرات المئات من المرات في اليوم ، فلماذا يجب علينا إعادة الحساب في كل مرة يتم فيها استدعاء البرنامج النصي ، إذا كان من الممكن تخزين كائن النتيجة في ملف. من الأفضل سحب كائن من القرص ، ولكن ... يجب أن نكون على يقين من أهميته. فجأة تتم إعادة كتابة البرنامج النصي ويكون الكائن المحفوظ قديمًا. بناءً على ذلك ، لا يمكننا فقط تحميل الكائن عند وجود ملف. وتأتي النقطة الثانية من هذا. - تعقب التغييرات في شجرة الحساب:
يجب أن يتم حساب الحاجة إلى تحديث الكائن على أساس البيانات حول وسيطات الدالة التي تنشئها. لذلك سنكون على يقين من أن الكائن المحمل صالح. في الواقع ، بالنسبة للوظيفة الصرفة ، تعتمد القيمة المرجعة فقط على الحجج. هذا يعني أنه بينما نقوم بتخزين نتائج الدوال الخالصة ومراقبة التغييرات في الوسيطات ، يمكننا أن نكون هادئين بشأن صلة ذاكرة التخزين المؤقت. علاوة على ذلك ، إذا كان الكائن المحسوب يعتمد على كائن مخبأ آخر (كسول) ، والذي يعتمد بدوره على كائن آخر ، فأنت بحاجة إلى العمل بشكل صحيح على التغييرات في هذه الكائنات ، وتحديث عقد السلسلة التي توقفت عن كونها ذات صلة في الوقت المناسب. من ناحية أخرى ، سيكون من الجيد أن نأخذ في الاعتبار أننا لا نحتاج دائمًا إلى تحميل بيانات سلسلة الحساب بأكملها. في كثير من الأحيان ، يكفي تحميل كائن النتيجة النهائية فقط. - لديك بنية شفافة إلى حد ما:
هذه النقطة واضحة. إذا كان من الضروري إعادة كتابة النص برمته إلى الحسابات البطيئة لتغيير الشفرة بأكملها ، فهذا هو الحل. يجب إجراء التغييرات على الحد الأدنى.
أدى هذا الخط من المنطق إلى حل تقني ، تم تصميمه في بايثون بواسطة مكتبة Evalcache (الروابط في نهاية المقالة).
حل النحو وآلية العمل
مثال بسيطimport evalcache import hashlib import shelve lazy = evalcache.Lazy(cache = shelve.open(".cache"), algo = hashlib.sha256) @lazy def summ(a,b,c): return a + b + c @lazy def sqr(a): return a * a a = 1 b = sqr(2) c = lazy(3) lazyresult = summ(a, b, c) result = lazyresult.unlazy() print(lazyresult)
كيف يعمل؟
أول شيء يلفت انتباهك هنا هو إنشاء مصمم كسول. مثل هذا الحل النحوي هو معيار إلى حد ما بالنسبة لثعبان Python. يتم تمرير الديكور البطيء إلى كائن مخبأ يخزن فيه lenificator نتائج الحسابات. يتم فرض متطلبات الواجهة الشبيهة بالإملاء على نوع ذاكرة التخزين المؤقت. بمعنى آخر ، يمكننا تخزين كل شيء يقوم بتنفيذ نفس الواجهة مثل نوع الإملاء. للتوضيح في المثال أعلاه ، استخدمنا القاموس من مكتبة الرفوف.
يتم أيضًا إرسال الديكور إلى بروتوكول التجزئة الذي سيستخدمه لإنشاء مفاتيح التجزئة للأشياء وبعض الخيارات الإضافية (إذن الكتابة ، إذن القراءة ، إخراج التصحيح) ، والتي يمكن العثور عليها في الوثائق أو التعليمات البرمجية.
يمكن تطبيق الديكور على كل من الوظائف والأشياء من الأنواع الأخرى. في هذه اللحظة ، يتم بناء كائن كسول على أساسه باستخدام مفتاح تجزئة محسوب على أساس التمثيل (أو استخدام دالة التجزئة المحددة خصيصًا لهذا النوع من الوظائف).
السمة الرئيسية للمكتبة هي أن الكائن الكسول يمكن أن يولد كائنات كسولة أخرى ، وسيتم خلط مفتاح التجزئة الخاص بالوالد (أو الوالدين) في مفتاح التجزئة للسليل. بالنسبة للكائنات البطيئة ، يُسمح باستخدام عملية أخذ سمة واستخدام مكالمات ( __call__ ) للكائنات واستخدام عوامل التشغيل.
عند المرور من خلال برنامج نصي ، في الواقع ، لا يتم إجراء أي حسابات. بالنسبة إلى b ، لا يتم حساب المربع ، وبالنسبة لـ lazyresult ، لا يتم النظر في مجموع الحجج. بدلاً من ذلك ، يتم بناء شجرة العمليات ويتم حساب مفاتيح تجزئة الكائنات البطيئة.
الحسابات الحقيقية (إذا لم يتم وضع النتيجة في ذاكرة التخزين المؤقت مسبقًا) سيتم إجراؤها فقط في السطر: result = lazyresult.unlazy()
إذا تم حساب الكائن مسبقًا ، فسيتم تحميله من الملف.
يمكنك تصور شجرة البناء:
بناء تصور شجرة evalcache.print_tree(lazyresult) ... generic: <function summ at 0x7f1cfc0d5048> args: 1 generic: <function sqr at 0x7f1cf9af29d8> args: 2 ------- 3 -------
نظرًا لأن تجزئات الكائنات مبنية على أساس البيانات حول الحجج التي تولد هذه الكائنات ، عندما تتغير الوسيطة ، يتغير تجزئة الكائن ومعها تجزئات السلسلة بالكامل اعتمادًا عليها. يتيح لك هذا الحفاظ على تحديث بيانات ذاكرة التخزين المؤقت عن طريق إجراء التحديثات في الوقت المحدد.
كائنات كسولة تصطف في شجرة. إذا قمنا بإجراء عملية غير كسولة على أحد الكائنات ، فسيتم تحميل العديد من الكائنات وإحصائها حسب الضرورة للحصول على نتيجة صالحة. من الناحية المثالية ، سيتم تحميل الكائن الضروري ببساطة. في هذه الحالة ، لن تقوم الخوارزمية بسحب الأجسام المتشكلة إلى الذاكرة.
في العمل
أعلاه كان مثالًا بسيطًا يوضح بناء الجملة ولكنه لا يوضح القوة الحسابية للنهج.
هنا مثال أقرب قليلاً إلى الحياة الحقيقية (يستخدمه sympy).
مثال باستخدام sympy و numpy إن عمليات تبسيط التعبيرات الرمزية مكلفة للغاية وتطلب حرفياً التساهل. يستغرق المزيد من بناء مجموعة كبيرة وقتًا أطول ، ولكن بفضل التصغير ، سيتم سحب النتائج من ذاكرة التخزين المؤقت. يرجى ملاحظة أنه إذا تم تغيير أي معاملات في أعلى البرنامج النصي حيث يتم إنشاء تعبير sympy ، فسيتم إعادة حساب النتائج لأن مفتاح التجزئة للكائن الكسول سيتغير (بفضل __repr__ ).
في كثير من الأحيان ، يحدث موقف عندما يقوم الباحث بإجراء تجارب حسابية على كائن تم إنشاؤه لفترة طويلة. يمكنه استخدام العديد من البرامج النصية لفصل توليد واستخدام الكائن ، مما قد يسبب مشاكل في تحديث البيانات في وقت غير مناسب. النهج المقترح يمكن أن يسهل هذه الحالة.
ما هو كل هذا؟
Evalcache جزء من مشروع zencad. هذا هو برنامج نصي صغير ، مستوحى ويستغل نفس أفكار opencad. على عكس opencad الموجه بالشبكة ، يستخدم zencad الذي يعمل على قلب opencascade تمثيل brep للأشياء ، وتتم كتابة البرامج النصية في python.
غالبًا ما يتم تنفيذ العمليات الهندسية لفترة طويلة. عيب أنظمة البرمجة النصية cad هو أنه في كل مرة تقوم فيها بتشغيل البرنامج النصي ، يتم إعادة سرد المنتج بالكامل مرة أخرى. علاوة على ذلك ، مع نمو النموذج ومضاعفاته ، لا تنمو التكاليف العامة بشكل خطي. هذا يؤدي إلى حقيقة أنه يمكنك العمل بشكل مريح فقط مع الموديلات الصغيرة للغاية.
كانت مهمة Evalcache لتخفيف هذه المشكلة. في zencad ، يتم إعلان كل العمليات كسولة.
أمثلة:
مثال بناء نموذجي
ينشئ هذا البرنامج النصي النموذج التالي:
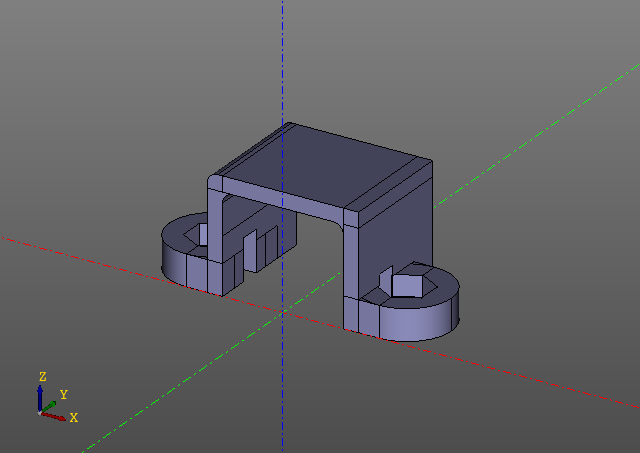
لاحظ أنه لا يوجد مكالمات تقييم في البرنامج النصي. الحيلة هي أن lenification مدمج في مكتبة zencad نفسها وأنه غير مرئي حتى للوهلة الأولى ، على الرغم من أن كل العمل هنا يعمل مع كسلان ، ولا يتم الحساب المباشر إلا في وظيفة "العرض". بالطبع ، إذا تم تغيير بعض معلمات النموذج ، فسيتم إعادة سرد النموذج من المكان الذي تغير فيه مفتاح التجزئة الأول.
نماذج الحوسبة الضخمةهنا مثال آخر. هذه المرة سنقتصر على الصور:
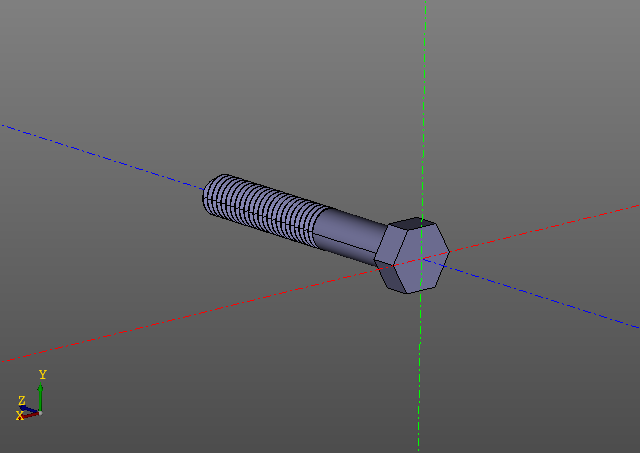
حساب السطح الملولب ليس مهمة سهلة. على جهاز الكمبيوتر الخاص بي ، يتم إنشاء مثل هذا الترباس على أساس عشر ثوانٍ ... يعد تحرير نموذج بخيوط أكثر متعة باستخدام التخزين المؤقت.
والآن هذه معجزة:

يعد عبور الأسطح الملولبة عملية حسابية معقدة. القيمة العملية ، ومع ذلك ، لا شيء سوى التحقق من الرياضيات. يستغرق الحساب دقيقة ونصف. هدف جدير بالتسامح.
المشاكل
قد لا تعمل ذاكرة التخزين المؤقت على النحو المنشود.
يمكن تقسيم أخطاء ذاكرة التخزين المؤقت إلى إيجابية خاطئة وسلبية خاطئة .
أخطاء سلبية كاذبة
الأخطاء السلبية الكاذبة هي المواقف التي تكون نتيجة الحساب فيها في ذاكرة التخزين المؤقت ، لكن النظام لم يعثر عليها.
يحدث هذا إذا أنتجت خوارزمية مفتاح التجزئة التي تستخدمها Evalcache لسبب ما مفتاحًا مختلفًا لإعادة الحساب. إذا لم يتم تجاوز دالة التجزئة للكائن من النوع المخزن مؤقتًا ، فإن Evalcache يستخدم __repr__ للكائن __repr__ المفتاح.
يحدث خطأ ، على سبيل المثال ، إذا لم تتجاوز الفئة المستأجرة object.__repr__ القياسي object.__repr__ ، والذي يتغير من البداية إلى البداية. أو ، إذا كان __repr__ ، يعتمد بطريقة ما على تافه لحساب البيانات المتغيرة (مثل عنوان الكائن أو الطابع الزمني).
سيء:
class A: def __init__(self): self.i = 3 A_lazy = lazy(A) A_lazy().unlazy()
جيد:
class A: def __init__(self): self.i = 3 def __repr__(self): return "A({})".format(self.i) A_lazy = lazy(A) A_lazy().unlazy()
تؤدي الأخطاء السلبية الكاذبة إلى حقيقة أن التسامح لا يعمل. سيتم إعادة سرد الكائن في كل تنفيذ نصي جديد.
أخطاء إيجابية كاذبة
هذا هو نوع أكثر خطأ من الخطأ ، لأنه يؤدي إلى أخطاء في كائن الحساب النهائي:
يمكن أن يحدث لسببين.
- مذهل:
حدث تصادم مفتاح تجزئة في ذاكرة التخزين المؤقت. بالنسبة لخوارزمية sha256 التي تحتوي على مساحة 115792089237316195423570985008687907853269984665640564039457584007913129639936 المفاتيح المحتملة ، فإن احتمال حدوث تصادم لا يكاد يذكر. - محتمل:
تمثيل كائن (أو دالة تجزئة متجاوزة) لا يصفه بالكامل ، أو يتزامن مع تمثيل كائن من نوع آخر.
class A: def __init__(self): self.i = 3 def __repr__(self): return "({})".format(self.i) class B: def __init__(self): self.i = 3 def __repr__(self): return "({})".format(self.i) A_lazy = lazy(A) B_lazy = lazy(B) a = A_lazy().unlazy() b = B_lazy().unlazy()
ترتبط __repr__ بكائن __repr__ غير متوافق. إذا كان من المستحيل لسبب ما استبدال نوع كائن __repr__ ، تسمح لك المكتبة بتعيين وظيفة تجزئة خاصة لنوع المستخدم.
حول نظائرها
هناك العديد من مكتبات lenification التي تعتبر في الأساس أنها كافية لتشغيل عملية حسابية لا أكثر من مرة واحدة لكل مكالمة البرنامج النصي.
هناك العديد من مكتبات التخزين المؤقت للقرص التي ستقوم ، بناء على طلبك ، بحفظ كائن بالمفتاح الضروري لك.
ولكن ما زلت لا أستطيع العثور على مكتبات تسمح بنتائج التخزين المؤقت على شجرة التنفيذ. إذا كان هناك أي من فضلك غير آمنة.
المراجع:
مشروع جيثب
مشروع Pypi