أسرع أرقام النقطة العائمة في الغرب المتوحش

في عملية تنفيذ "قارئ" واحد ، نشأت مشكلة مع زيادة دقة الحسابات. عملت خوارزمية الحساب بسرعة على أرقام الفاصلة العائمة القياسية ، ولكن عندما تم ربط المكتبات لإجراء حسابات دقيقة ، بدأ كل شيء يتباطأ بشكل كبير. في هذه المقالة ، سننظر في الخوارزميات لتوسيع أرقام الفاصلة العائمة باستخدام نهج متعدد المكونات ، والذي كان من الممكن تحقيق التسارع ، حيث يتم تنفيذ الحساب العائم على شريحة cp. سيكون هذا النهج مفيدًا لحساب أكثر دقة للمشتقات العددية أو عكس المصفوفة أو تقليم المضلع أو غيرها من المشاكل الهندسية. لذلك من الممكن محاكاة تعويم 64 بت على بطاقات الفيديو التي لا تدعمها.

مقدمة

كما نصحنا نيكلاس ويرث لنا بالحفاظ على الأرقام 0 و 1 ، لذلك نقوم بتخزينها فيها. وهل يعيش البشر في النظام العشري ، والأرقام التي تبدو عادية 0.1 و 0.3 لا يمكن تمثيلها في النظام الثنائي بجزء محدود؟ نشعر بصدمة ثقافية عندما نقوم بالحسابات عليها. بالطبع ، يتم بذل محاولات لإنشاء مكتبات للمعالجات على أساس النظام العشري ولدى IEEE تنسيقات موحدة.

ولكن في الوقت الحالي ، نأخذ التخزين الثنائي في الاعتبار في كل مكان ونجري جميع حسابات المال مع المكتبات لإجراء العمليات الحسابية الدقيقة ، مثل bignumber ، مما يؤدي إلى فقدان الأداء. يعتبر Asiks التشفير ، وفي المعالجات لا توجد سوى مساحة صغيرة جدًا لهذا الحساب العشري الخاص بك ، كما يقول المسوقون. لذلك ، فإن النهج متعدد المكونات ، عندما يتم تخزين الرقم في شكل مجموع غير قابل للتحويل من الأرقام ، هو خدعة ملائمة ومجال متطور بنشاط في مجال المعلوماتية النظرية. على الرغم من أن ديكر ما زال يتعلم التكاثر بشكل صحيح ، دون فقدان الدقة ، في عام 1971 ، ظهرت المكتبات الجاهزة للاستخدام في وقت لاحق (MPFR ، QD) وليس بجميع اللغات ، على ما يبدو حيث لم تدعم جميع معايير IEEE ، ولكن الأدلة الصارمة على خطأ الحساب حتى في وقت لاحق ، على سبيل المثال في عام 2017 لحساب مزدوج الكلمات.

الحساب مزدوج الكلمات

ما هي النقطة؟ في أوقات اللحى ، عندما لم تكن هناك معايير للأرقام العائمة ، لتجنب المشاكل في تنفيذ التقريب ، توصل Møller ، وأثبت Knuth لاحقًا أنه يوجد تجميع خالٍ من الأخطاء. يركض بهذه الطريقة

function quickTwoSum(a, b) { let s = a + b; let z = s - a; let e = b - z; return [s, e]; } 

في هذه الخوارزمية ، افترض أنه إذا $$$| a | > | b |$، ثم يمكن تمثيل مجموعهم بالضبط كمجموع رقمين $$$s + e$ويمكنك تخزينها في أزواج للحسابات اللاحقة ، ويتم تقليل الطرح بالإضافة إلى رقم سالب.



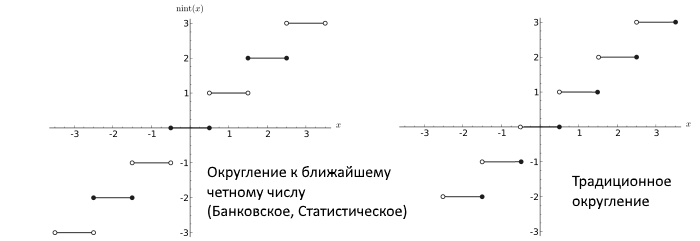
في وقت لاحق ، أظهر Dekker أنه إذا تم استخدام أرقام الفاصلة العائمة التي تستخدم التقريب إلى أقرب رقم زوجي (روابط تقريب إلى أقرب إلى زوج ، وهو إجراء صحيح بشكل عام لا يؤدي إلى أخطاء كبيرة في عملية الحسابات الطويلة ومعيار IEEE) ، ثم هناك خوارزمية الضرب خالية من الأخطاء.

 function twoMult(a, b) { let A = split(a); let B = split(b); let r1 = a * b; let t1 = -r1 + A[0] * B[0]; let t2 = t1 + A[0] * B[1]; let t3 = t2 + A[1] * B[0]; return [r1, t3 + A[1] * B[1]]; } 

حيث أن Split () هي خوارزمية السيد Weltkamp لتقسيم رقم

 let splitter = Math.pow(2, 27) + 1; function split(a) { let t = splitter * a; let d = a - t; let xh = t + d; let xl = a - xh; return [xh, xl]; } 

باستخدام ثابت $$$C = 2 ^ s + 1$وهو ما يساوي أكثر بقليل من نصف طول الجزء العشري ، والذي لا يؤدي إلى تجاوز الأرقام في عملية الضرب ويقسم الجزء العشري إلى نصفين. على سبيل المثال ، مع كلمة بطول 64 بت ، يبلغ طول الجزء العشري 53 ثم s = 27.



بهذه الطريقة ، قدم Dekker المجموعة الكاملة تقريبًا اللازمة للحوسبة في الحساب مزدوج الكلمات. منذ ذلك الحين ، تمت الإشارة أيضًا إلى كيفية ضرب ، وتقسيم وترقيم رقمين مزدوجين.

كانت خوارزمية QuickTwoSum الخاصة به لجمع كلمتين مزدوجتين في كل مكان "مضمنة" ، وتم استخدام الشيك $$$| a | > | b |$. على المعالجات الحديثة ، كما هو موضح في [4] ، من الأرخص استخدام عمليات إضافية بأرقام من تفريع الخوارزمية. لذلك ، أصبحت الخوارزمية التالية الأنسب لإضافة رقمين من كلمة واحدة

 function twoSum(a, b) { let s = a + b; let a1 = s - b; let b1 = s - a1; let da = a - a1; let db = b - b1; return [s, da + db]; } 

وهذا هو الجمع والضرب للأرقام المزدوجة الكلمات.

 function add22(X, Y) { let S = twoSum(X[0], Y[0]); let E = twoSum(X[1], Y[1]); let c = S[1] + E[0]; let V = quickTwoSum(S[0], c); let w = V[1] + E[1]; return quickTwoSum(V[0], w); } function mul22(X, Y) { let S = twoMult(X[0], Y[0]); S[1] += X[0] * Y[1] + X[1] * Y[0]; return quickTwoSum(S[0], S[1]); } 

بشكل عام ، تم وصف القائمة الأكثر اكتمالًا ودقة للخوارزميات لحساب الكلمات المزدوجة وحدود الخطأ النظرية والتطبيق العملي في الرابط [3] من عام 2017. لذلك ، إذا كنت مهتمًا ، أوصي بشدة بالذهاب مباشرة إلى هناك. بشكل عام ، يتم إعطاء خوارزمية للكلمة الرباعية في [6] ، وفي [5] لتمديد متعدد المكونات للطول التعسفي. هناك فقط ، بعد كل عملية ، يتم استخدام عملية إعادة التنسيق ، والتي ليست دائمًا مثالية للأحجام الصغيرة ، ولا يتم تحديد دقة الحسابات في QD بشكل صارم. بشكل عام ، يجدر التفكير في حدود قابلية تطبيق هذه المناهج بالطبع.

قصص رعب javascript-a. مقارنة بين عشري. js مقابل bignumber.js مقابل big.js.

حدث ذلك أن جميع المكتبات تقريبًا للحسابات الدقيقة في شبيبة مكتوبة من قبل شخص واحد. يتم إنشاء وهم الاختيار ، على الرغم من أنهم جميعا تقريبا نفس. بالإضافة إلى ذلك ، لا تشير الوثائق بشكل صريح إلى أنه إذا لم تقم بتقريب الأرقام بعد كل عملية ضرب / قسمة ، فسيتم مضاعفة حجم رقمك طوال الوقت ، ويمكن أن يتطور تعقيد الخوارزمية إلى واحد سهل في x3500. على سبيل المثال ، قد تبدو مقارنة وقت حسابها على هذا النحو إذا لم تقم بتقريب الأرقام.



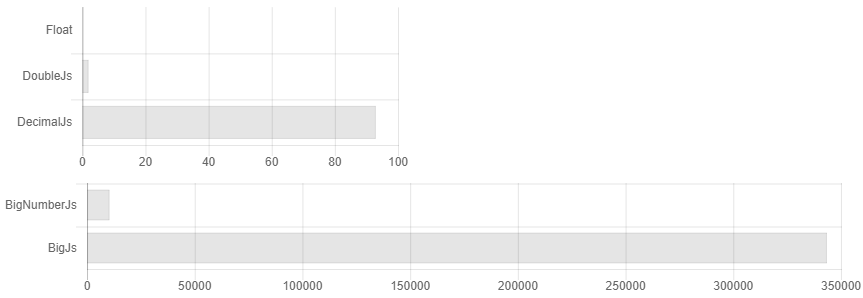
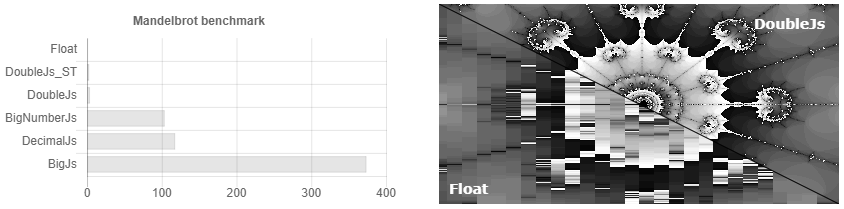
أي أنك قمت بتعيين الدقة إلى 32 خانة عشرية و ... عفوًا ، لديك بالفعل 64 رقمًا ، 128. نحن نعتقد بدقة عالية! 256 ، 512 ... لكنني قمت بتعيين 32! .. 1024 ، 2048 ... شيء من هذا القبيل يظهر فوق الرأس 3500 مرة. تنص الوثائق على أنه إذا كان لديك حسابات علمية ، فمن المحتمل أن يكون العشري. js أفضل لك. على الرغم من أنه في الواقع ، إذا انتهيت للتو بشكل دوري ، للحسابات العلمية Bignumber.js يعمل بشكل أسرع قليلاً (انظر الشكل 1). من يحتاج إلى حساب المئات من الفلس إذا لم يكن بالإمكان تغييرها؟ هل هناك أي حالة عندما أحتاج إلى تخزين المزيد من الأرقام المشار إليها ولا يمكنني الخروج مع بعض الأحرف الإضافية؟ كيف يأخذ جيب مثل هذا الرقم الوحش ، عندما لا يعرف أحد الدقة الصارمة لتقارب سلسلة تايلور للأرقام التعسفية؟ بشكل عام ، لا توجد شكوك لا أساس لها من الصحة أنه من الممكن زيادة سرعة الحساب هناك ، باستخدام خوارزميات الضرب Schoenhage-Strassen وإيجاد الجيب مع الحسابات الكوردية ، على سبيل المثال.

Double.js

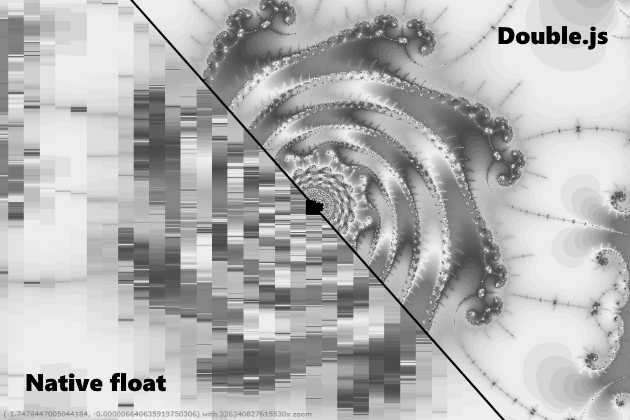
أود أن أقول بالطبع أن برنامج Double.js يحسب بسرعة ودقة. لكن هذا ليس صحيحًا تمامًا ، أي أنه أسرع بعشر مرات من ذلك ، ولكنه ليس دقيقًا دائمًا. على سبيل المثال ، 0.3-0.1 يمكن معالجتها ، والانتقال إلى تخزين مزدوج والعكس صحيح. ولكن يمكن حل رقم Pi بدقة مزدوجة تصل إلى 32 رقمًا تقريبًا ولا يعمل مرة أخرى. يتم إنشاء خطأ في السادس عشر ، كما لو حدث تجاوز في الحد. بشكل عام ، أحث مجتمع js على العمل معًا لمحاولة حل مشكلة التحليل ، لأنني عالق. حاولت التحليل الرقمي وتقسيمه بدقة مزدوجة ، كما هو الحال في QD ، وتقسيمه على دفعات من 16 رقمًا وتقسيمها بدقة مزدوجة ، وتقسيم الجزء العشري باستخدام Big.js كما هو الحال في إحدى مكتبات جوليا. الآن أخطأ في خطأ في .parseFloat () ، نظرًا لأن معايير IEEE مع التقريب إلى أقرب عدد صحيح مدعومة حتى مع ECMAScript 1. على الرغم من أنه يمكنك بالطبع محاولة ربط المخزن المؤقت الثنائي ومشاهدة كل 0 و 1. بشكل عام ، إذا كان يمكنك حل هذه المشكلة ، ثم سيكون من الممكن بعد ذلك إجراء حسابات بدقة تعسفية مع التسارع في x10-x20 من bignumber.js. ومع ذلك ، فإن العديد من Mandelbrot يقدم بالفعل الجودة ، ويمكنك استخدامه للمهام الهندسية.

بعد مرور عام ، عدت إلى هنا ولا زلت أصلح مشكلة التحليل. كانت المشكلة في دقة غير كافية ، عند ضربها في 10 ^ (- n). تم تعديل جميع الخوارزميات من الصفر ، وتعمل الآن بدقة وسرعة مخيفة.



هنا رابط إلى lib ، هناك معيار تفاعلي و sandbox حيث يمكنك اللعب به.

المصادر المستخدمة

1. O. Møller. شبه مضاعفة الدقة في العمليات الحسابية للفاصلة العائمة. 1965.
2. ثيودوروس ديكر. تقنية الفاصلة العائمة لتمديد الدقة المتوفرة ، 1971. [ عارض ]
3. ميوارا جولديس ، جان ميشيل مولر ، فالنتينا بوبيسكو. حدود خطأ صارمة ودقيقة للكتل الأساسية لبناء الحساب مزدوج الكلمات ، 2017. [ PDF ]
4. مولر ، جي. Brisebarre ، N. de Dinechin ، إلخ. كتيب حساب الفاصلة العائمة ، الفصل 14 ، 2010.
5. جوناثان شيوتشوك. التنبؤات الهندسية العائمة المتكيفة القوية ، 1964. [ PDF ]
6. يوزو هيدا ، شياويي لي ، ديفيد بيلي. مكتبة الحساب المزدوج المزدوج والرباعي المزدوج ، 2000. [ PDF ]