ما لرسم الصور المتجهة؟ بالنسبة لي ، كما هو الحال بالنسبة لكثيرين آخرين ، فإن الإجابة واضحة للغاية: على الأرجح في الرسام. حسنًا ، أو في Inskape. فكرت أيضًا عندما أمرت برسم ثمانمائة قطعة لكتاب الفيزياء. لا شيء من هذا القبيل ، فقط الرسوم التوضيحية الفنية بالأبيض والأسود مع جميع أنواع الكتل والكرات والينابيع والعدسات والسيارات والجرارات وما شابه ذلك. كان من المفترض أن يتألف الكتاب من لاتك ، وقد زُودت بملفات Word مع صور مدرجة - إما في رسومات بالقلم الرصاص ، أو بمسح من كتب أخرى - وبدا أن المخطوطة في شكل ما. في هذه الحالة ، استسلم الفكر الأول - وهو الرسم في الفضاء - إلى الأوهام حول موضوع "كيف يمكن لهذا أتمتة كل شيء؟" لسبب ما ، يبدو أن
MetaPost هو الخيار الأفضل في تلك اللحظة.
أهم إضافة لهذا الحل هو أن كل صورة يمكن أن تكون وظيفة صغيرة للعديد من المتغيرات ؛ مثل هذه الصورة من السهل ، على سبيل المثال ، تغيير الحجم وتناسب الخطوط مع ظروف محددة لم تكن معروفة من قبل دون انتهاك نسب مهمة ، وهو أمر يصعب تحقيقه بوسائل أكثر تقليدية. والعناصر المكررة - نفس الكرات والينابيع - يمكن جعلها تتصرف بشكل أكثر إثارة للاهتمام مما تسمح به وسائل التحرير "البشرية".
كنت أرغب في عمل صور مع الفقس ، مثل تلك الموجودة في الكتب القديمة.

أولاً ، كان علينا الحصول على خطوط ذات سمك متغير. تتمثل الصعوبة الرئيسية هنا في إنشاء منحنى أكثر أو أقل توازيًا للمنحنى المحدد ، وعند الضرورة ، تغيير المسافة إلى المنحنى المحدد. لقد اعتمدت على
الطريقة الأكثر بدائية ، على الأرجح ، التي يتم من خلالها نقل الأجزاء التي تربط النقاط المتوسطة لمنحنى بيزييه ببساطة على مسافة معينة بالتوازي. مع اختلاف أن هذه المسافة يمكن أن تختلف على طول المنحنى.
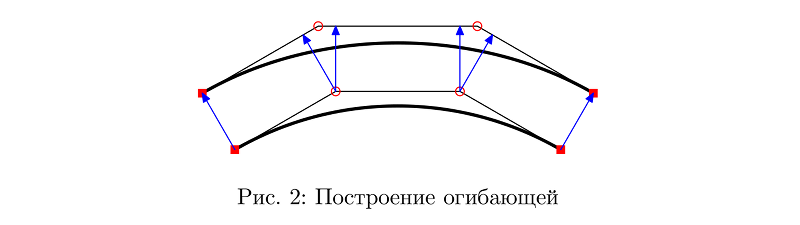
في معظم الحالات ، يسمح هذا بنتيجة لائقة.
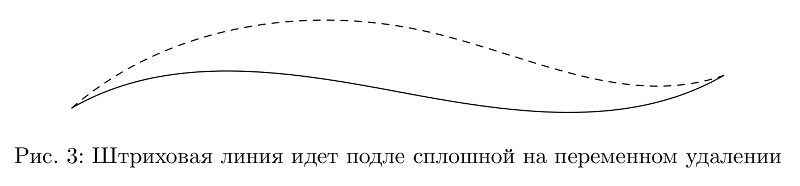
رمز المثالفيما يلي يُفترض أنه تم
تنزيل المكتبة وهناك خط
input fiziko.mp; مكان ما
input fiziko.mp; . أسرع طريقة للبدء والنظر في ConTeXt (عندئذٍ ليست هناك حاجة إلى
beginfig و
endfig ):
\starttext
\startMPcode
input fiziko.mp;
\stopMPcode
\stoptext
أو في LuaLaTeX:
\documentclass{article}
\usepackage{luamplib}
\begin{document}
\begin{mplibcode}
input fiziko.mp;
\end{mplibcode}
\end{document}
beginfig(3);
path p, q; % , , ,
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q := offsetPath(p)(1cm*sin(offsetPathLength*pi)); % — , — (offsetPathLength, 0 1), ,
draw p;
draw q dashed evenly;
endfig;
الآن يمكن استخدام اثنين من هذه المنحنيات لعمل كفاف لخط سمك متغير.

رمز المثالbeginfig(4);
path p, q[];
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q1 := offsetPath(p)(1/2pt*(sin(offsetPathLength*pi)**2)); %
q2 := offsetPath(p)(-1/2pt*(sin(offsetPathLength*pi)**2)); %
fill q1--reverse(q2)--cycle;
endfig;
يجب أن يكون السمك محدودًا إلى حد ما من الأسفل ، وإلا فإن المسح النقطي سيأخذ أجزاء رقيقة جدًا من الخطوط عند الطباعة ، وعادة ما يكون هذا ليس جميلًا جدًا. أحد الخيارات هو رسم جميع الخطوط ، التي يقل سمكها عن قيمة معينة ، بخطوط متقطعة لها نفس الحد الأدنى للسمك ، بحيث يتوافق إجمالي كمية الطلاء لكل وحدة طول في المتوسط مع الخط لسمك الهدف. أي ، بدلاً من تقليل كمية الطلاء من جانبي الخط ، ابدأ في تقضمه بخطوط مستعرضة.

رمز المثالbeginfig(5);
path p;
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
draw brush(p)(1pt*(sin(offsetPathLength*pi)**2)); % , ,
endfig;
الآن يمكنك رسم الكرات. يمكن أن تكون مجرد دوائر متحدة المركز ، يتم تحديد سمك الخطوط من خلال وظيفة إضاءة الكرة عند النقاط التي تمر من خلالها الخطوط.
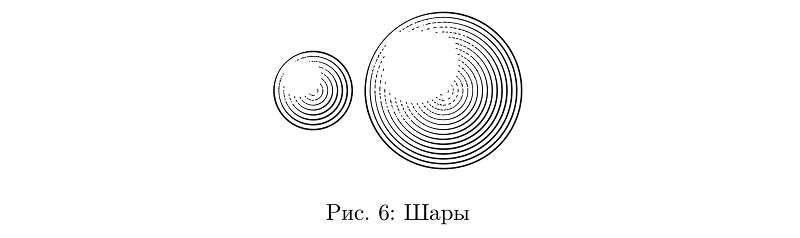
رمز المثالbeginfig(6);
draw sphere.c(1.2cm);
draw sphere.c(2.4cm) shifted (2cm, 0);
endfig;
بدائية أخرى ملائمة هي "الخراطيم": بشكل تقريبي ، أسطوانات يمكن ثنيها بأي شكل من الأشكال. طالما أنها ذات مقطع عرضي ثابت ، كل شيء بسيط معهم.
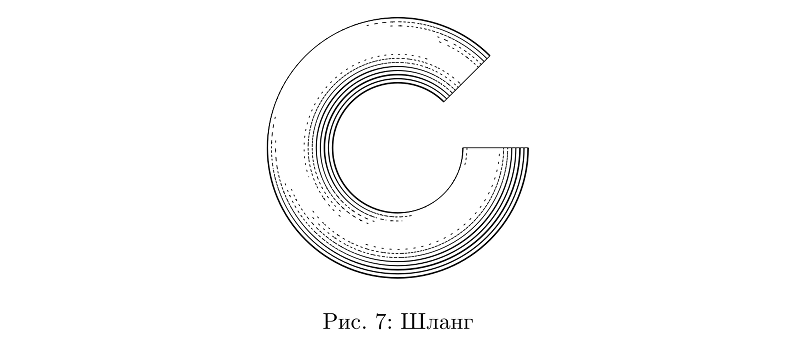
رمز المثالbeginfig(7);
path p;
p := subpath (1,8) of fullcircle scaled 3cm;
draw tube.l(p)(1/2cm); % — ,
endfig;
إذا تغير السماكة ، فيجب تغيير عدد السكتات الدماغية وفقًا لذلك ، مع الحفاظ على متوسط كثافة التعبئة دون تغيير ، وكذلك مراعاة التغيرات في السماكة عند حساب الإضاءة.
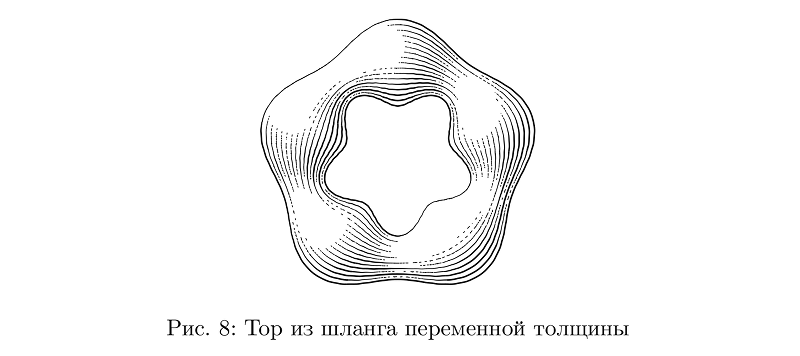
رمز المثالbeginfig(8);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm;
draw tube.l(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
لا تزال هناك خراطيم مع الفقس العرضي ، ولكن بالنسبة لهم كان من الصعب حل مشكلة الحفاظ على متوسط كثافة التعبئة ، لذلك في كثير من الحالات لا تزال تبدو جيدة جدًا.
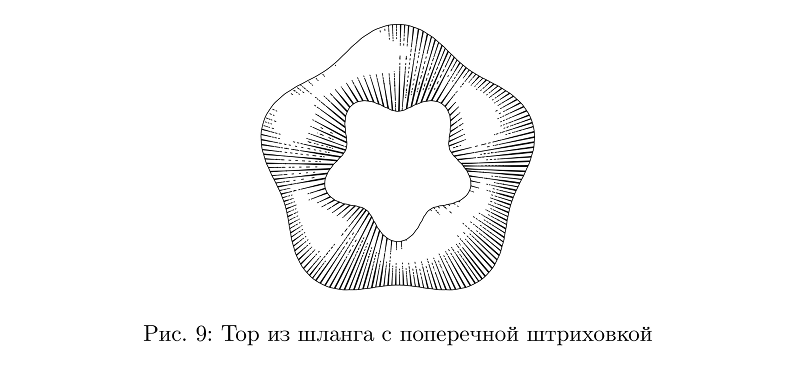
رمز المثالbeginfig(9);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm;
draw tube.t(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
من حيث المبدأ ، يمكن صنع الكثير من الخراطيم وحدها: من المخاريط والأسطوانات إلى الدرابزينات.
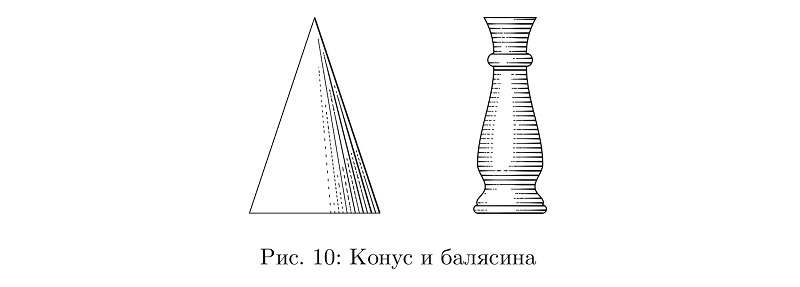
رمز المثالbeginfig(10);
draw tube.l ((0, 0) -- (0, 3cm))((1-offsetPathLength)*1cm) shifted (-3cm, 0); %
path p;
p := (-1/2cm, 0) {dir(175)} .. {dir(5)} (-1/2cm, 1/8cm) {dir(120)} .. (-2/5cm, 1/3cm) .. (-1/2cm, 3/4cm) {dir(90)} .. {dir(90)}(-1/4cm, 9/4cm){dir(175)} .. {dir(5)}(-1/4cm, 9/4cm + 1/5cm){dir(90)} .. (-2/5cm, 3cm); %
p := pathSubdivide(p, 6);
draw p -- reverse(p xscaled -1) -- cycle;
tubeGenerateAlt(p, p xscaled -1, p rotated -90); % , tube.t, — — , — .
endfig;
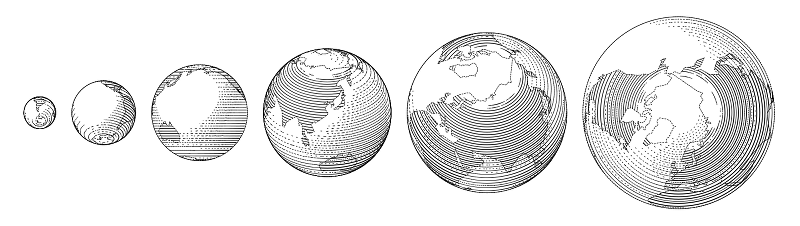
بعض ما يمكن بناؤه من هذه الأجزاء موجود في المكتبة. لنفترض أن الكرة الأرضية هي في الأساس كرة.
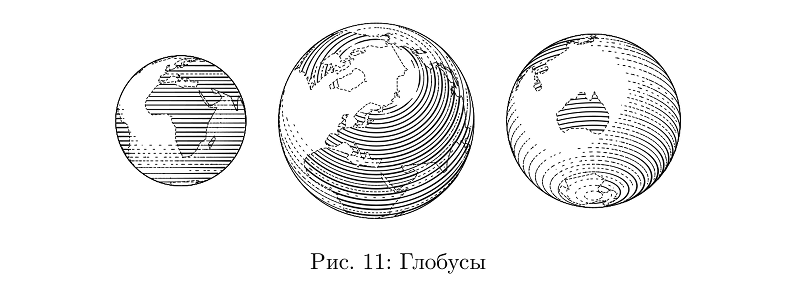
رمز المثالbeginfig(11);
draw globe(1cm, -15, 0) shifted (-6/2cm, 0); % , ,
draw globe(3/2cm, -30.28367, 59.93809);
draw globe(4/3cm, -140, -30) shifted (10/3cm, 0);
endfig;
على الرغم من عدم القيام بذلك: هنا يتم تشغيل الفقس بالتوازي ، والتحكم في سمك السكتة الدماغية للحفاظ على كثافة التعبئة أكثر صعوبة مما هو عليه في حالة الفقس العرضي على الخراطيم ، لذلك هذا هو نوع منفصل من الكرة.
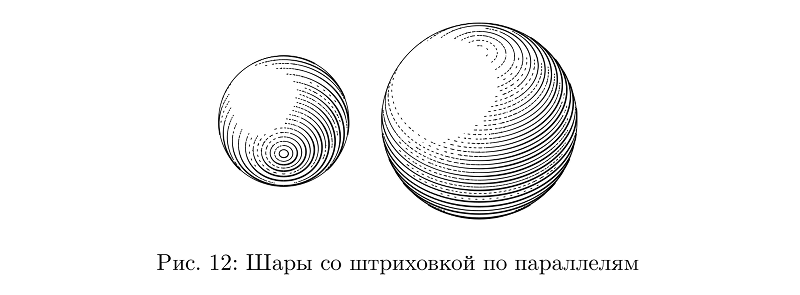
رمز المثالbeginfig(12);
draw sphere.l(2cm, -60); %
draw sphere.l(3cm, 45) shifted (3cm, 0);
endfig;
والوزن هو تصميم مباشر لنوعين من الخراطيم ذات سمك متغير.
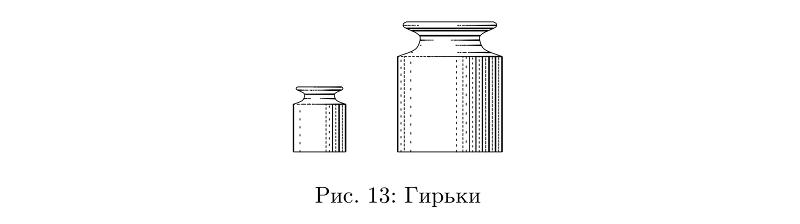
رمز المثالbeginfig(13);
draw weight.s(1cm); %
draw weight.s(2cm) shifted (2cm, 0);
endfig;
لا تزال هناك أداة لربط الخراطيم بالعقد.
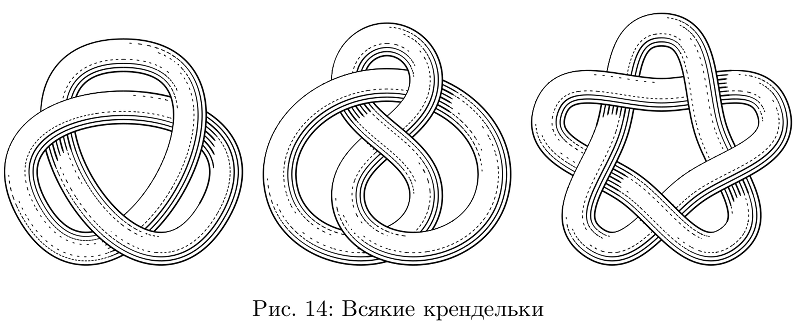
عينة من التعليمات البرمجية حتى لا تحدث فوضى ، عقدة واحدة فقطbeginfig(14);
path p;
p := (dir(90)*4/3cm) {dir(0)} .. tension 3/2 ..(dir(90 + 120)*4/3cm){dir(90 + 30)} .. tension 3/2 ..(dir(90 - 120)*4/3cm){dir(-90 - 30)} .. tension 3/2 .. cycle;
p := p scaled 6/5;
addStrandToKnot (primeOne) (p, 1/4cm, "l", "1, -1, 1"); % primeOne , p 1/4cm, "l" ( tube.l, tube.t ) «» "1, -1, 1" p
draw knotFromStrands (primeOne); % .
endfig;
ظلال العقد هي بعض التعقيد في نموذج الإضاءة. من حيث المبدأ ، لا يزعج أحد استخدامها في حالات أخرى ، لكنني لم أحدد هدفًا للتعمق في وحدة التخزين ، لذلك في حين أن هذا ليس مناسبًا جدًا ، إلا أنه لا يعمل في كل مكان.
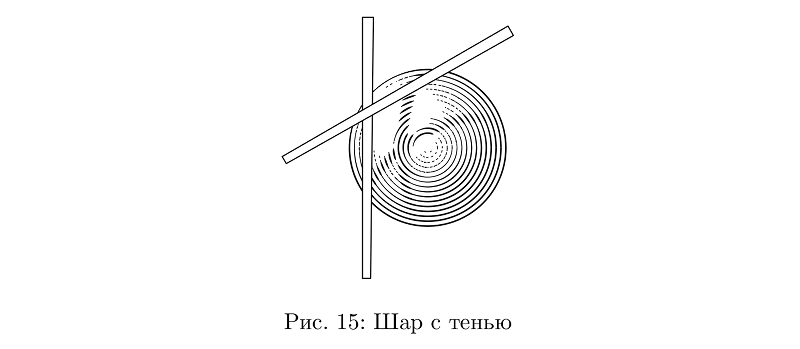
رمز المثالbeginfig(15);
path shadowPath[];
boolean shadowsEnabled;
numeric numberOfShadows;
shadowsEnabled := true; %
numberOfShadows := 1; %
shadowPath0 := (-1cm, -2cm) -- (-1cm, 2cm) -- (-1cm +1/6cm, 2cm) -- (-1cm + 1/8cm, -2cm) -- cycle; % , ,
shadowDepth0 := 4/3cm; % - «» ,
shadowPath1 := shadowPath0 rotated -60;
shadowDepth1 := 4/3cm;
draw sphere.c(2.4cm); % sphere.c tube.l
fill shadowPath0 withcolor white;
draw shadowPath0;
fill shadowPath1 withcolor white;
draw shadowPath1;
endfig;
وبالطبع ، تحتاج إلى نسيج خشبي. يعد تأثير طبيعة نمو العقد على نمط أقسام حلقات الأشجار موضوعًا للبحث الجاد. تبسيطًا جدًا ، يمكننا أن نتخيل حلقات سنوية في مستويات متوازية تدخل فيها تشوهات العقد. لذلك يكفي وصف التغيير في المستوى من خلال بعض الوظائف غير المعقدة للغاية (وظيفة العقدة) والنظر في سلسلة من العزلات لمجموع مجموعة هذه الوظائف مثل النمط المطلوب من حلقات الشجرة.
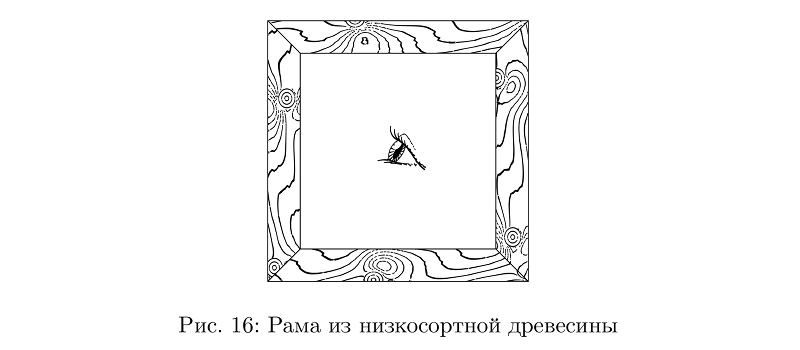
رمز المثالbeginfig(16);
numeric w, b;
pair A, B, C, D, A', B', C', D';
w := 4cm;
b := 1/2cm;
A := (0, 0);
A' := (b, b);
B := (0, w);
B' := (b, wb);
C := (w, w);
C' := (wb, wb);
D := (w, 0);
D' := (wb, b);
draw woodenThing(A--A'--B'--B--cycle, 0); % , A--A'--B'--B--cycle, 0
draw woodenThing(B--B'--C'--C--cycle, 90);
draw woodenThing(C--C'--D'--D--cycle, 0);
draw woodenThing(A--A'--D'--D--cycle, 90);
eyescale := 2/3cm; %
draw eye(150) shifted 1/2[A,C]; % 150
endfig;
يمكن أن تفتح العين من الصورة أعلاه قليلاً ، ثم الحول ، ويتغير عرض الحدقة. لا يوجد معنى خاص في هذا ، ولكن اتضح بشكل أكثر وضوحًا مما لو كانت مثل هذه التفاهات هي نفسها ميكانيكيًا في كل مكان.

رمز المثالbeginfig(17);
eyescale := 2/3cm; % 1/2cm
draw eye(0) shifted (0cm, 0);
draw eye(0) shifted (1cm, 0);
draw eye(0) shifted (2cm, 0);
draw eye(0) shifted (3cm, 0);
draw eye(0) shifted (4cm, 0);
endfig;
في معظم الأحيان ، لم تكن الصور معقدة للغاية ، ولكن إذا كنت تتعامل مع الأمر بكل جدية ، فيجب حل العديد من المهام لتوضيحها بشكل ذي معنى. هنا ، دعنا نقول ، مهمة Lopital حول الكتلة (لا أعرف كيف يتم استدعاؤها باللغة الروسية بشكل صحيح ، لم تكن في الكتاب المدرسي ، على سبيل المثال فقط): الكتلة معلقة على حبل بطول معلق عند النقطة A ، معلقة على حبل آخر معلقة على نفس الارتفاع عند النقطة B ، البضائع معلقة على الحبل الثاني ، والسؤال هو ، إذا كانت الحبال والكتلة عديمة الوزن ، أين ستكون الشحنة؟ من المثير للدهشة أن حل المشكلة والبناء ليسا بدائيين ، ولكن باللعب مع العديد من المتغيرات ، يمكنك بسهولة جعل الصورة بالضبط ما سيبدو أفضل على الشريط ، بينما تظل صحيحة.
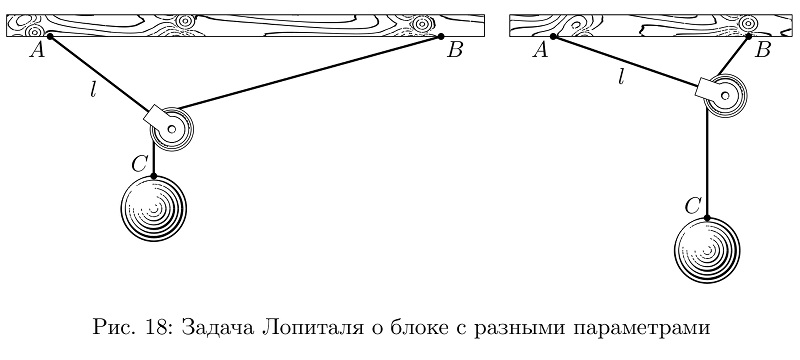
رمز المثالvardef lHopitalPulley (expr AB, l, m) = % AB l, m . ? : , , arithmetic overflow.
save A, B, C, D, E, o, a, x, y, d, w, h, support;
image(
pair A, B, C, D, E, o[];
path support;
numeric a, x[], y[], d[], w, h;
x1 := (l**2 + abs(l)*((sqrt(8)*AB)++l))/4AB; % ,
y1 := l+-+x1; %
y2 := m - ((AB-x1)++y1); %
A := (0, 0);
B := (AB*cm, 0);
D := (x1*cm, -y1*cm);
C := D shifted (0, -y2*cm);
d1 := 2/3cm; d2 := 1cm; d3 := 5/6d1; % ,
w := 2/3cm; h := 1/3cm; % . ,
o1 := (unitvector(CD) rotated 90 scaled 1/2d3);
o2 := (unitvector(DB) rotated 90 scaled 1/2d3);
E := whatever [D shifted o1, C shifted o1]
= whatever [D shifted o2, B shifted o2]; % ,
a := angle(AD);
support := A shifted (-w, 0) -- B shifted (w, 0) -- B shifted (w, h) -- A shifted (-w, h) -- cycle;
draw woodenThing(support, 0); % ,
draw pulley (d1, a - 90) shifted E; %
draw image(
draw A -- D -- B withpen thickpen;
draw D -- C withpen thickpen;
) maskedWith (pulleyOutline shifted E); %
draw sphere.c(d2) shifted C shifted (0, -1/2d2); %
dotlabel.llft(btex $A$ etex, A);
dotlabel.lrt(btex $B$ etex, B);
dotlabel.ulft(btex $C$ etex, C);
label.llft(btex $l$ etex, 1/2[A, D]);
)
enddef;
beginfig(18);
draw lHopitalPulley (6, 2, 11/2); % ,
draw lHopitalPulley (3, 5/2, 3) shifted (8cm, 0);
endfig;
ما هو الكتاب المدرسي؟ للأسف وآه ، عندما كانت جميع الرسوم التوضيحية والتخطيط جاهزة تقريبًا ، حدث شيء هناك ولم يخرج أبدًا. لذلك ، ربما ، في وقت لاحق ، أعدت كتابة جميع الأشياء الرئيسية من المكتبة الناتجة مرة أخرى
ونشرت الرمز على github . لم تدخل بعض kunshtyuki هناك: على سبيل المثال ، الدوائر الكهربائية أو وظيفة لرسم السيارات والجرارات. وأضاف بعض: العقد ، على سبيل المثال.
لا يعمل هذا المطبخ بالكامل بسرعة: يستغرق الأمر حوالي دقيقة لجمع كل الصور لهذه المقالة باستخدام LuaLaTeX على الكمبيوتر المحمول الخاص بي مع i5-4200U 1.6 جيجا هرتز. بالنسبة للعديد من الأشياء ، يتم استخدام مولد أرقام عشوائي عشوائي ، لذلك ستبدو الصور المتشابهة مختلفة قليلاً ليس فقط داخل جولة واحدة (هذه ميزة) ، ولكن كل تشغيل لاحق سيعطي صورًا مختلفة عن الصورة السابقة. ولكن يمكنك دائمًا تعيين
randomseed := - في الديباجة ، وستنتج كل المسارات نفسها الصور نفسها.