مهمة مع ناطحة سحاب وبيض - وليس سلة نيوتن؟

في الواقع ، هو الأكثر. لكن أول الأشياء أولاً.

بيان المشكلة

أتقن الثعبان ، وأحل كل شيء في Codewars. واجهت مهمة معروفة حول ناطحة سحاب وبيض. والفرق الوحيد هو أن بيانات المصدر ليست 100 طابق و 2 بيضة ، ولكن أكثر بقليل.
إعطاء: N بيض ، M يحاول رميهم ، ناطحة سحاب لا نهاية لها.

تحديد: الحد الأقصى الذي يمكنك من خلاله رمي بيضة دون كسر. البيض كروي في فراغ ، وإذا لم ينكسر أحدهم ، يسقط ، على سبيل المثال ، من الطابق 99 ، فإن الآخرين سيتحملون أيضًا سقوطًا من جميع الطوابق أقل من مائة.

0 <= N ، M <= 20000.
وقت تشغيل عشرين اختبارًا هو 12 ثانية.

ابحث عن حل

نحتاج إلى كتابة ارتفاع دالة (n، m) ، والتي ستعيد رقم الطابق لـ n ، m. نظرًا لأنه سيتم ذكره في كثير من الأحيان ، وفي كل مرة تكتب فيها كسول "الارتفاع" ، ففي كل مكان باستثناء الرمز ، سأقوم بتعيينه كـ f (n، m).

لنبدأ بالأصفار. من الواضح أنه إذا لم يكن هناك بيض أو محاولات لرميها ، فلا يمكن تحديد أي شيء وستكون الإجابة صفر. و (0 ، م) = 0 ، و (ن ، 0) = 0.

لنفترض أن هناك بيضة واحدة ، وهناك 10 محاولات. يمكنك المخاطرة بكل شيء ورميها على الفور من الطابق المائة ، ولكن في حالة الفشل ، لن تتمكن من تحديد أي شيء آخر ، لذلك فمن المنطقي أن تبدأ من الطابق الأول والصعود طابقًا واحدًا بعد كل رمية ، حتى تنتهي المحاولة أو البيضة. الحد الأقصى الذي يمكنك الحصول عليه إذا لم تفشل البيضة هو الطابق رقم 10. f (1، m) = m

خذ البيضة الثانية ، حاول مرة أخرى 10. الآن ، ثم يمكنك أخذ فرصة مع مائة؟ إذا انكسر ، فسيكون هناك محاولة أخرى و 9 محاولات ، 9 طوابق على الأقل ستكون قادرة على المرور. لذلك ربما تحتاج إلى المخاطرة ليس من المائة ، ولكن من العاشر؟ منطقي. ثم ، إذا نجحت ، ستبقى بيضتان و 9 محاولات. قياسا على ذلك ، تحتاج الآن إلى الصعود إلى 9 طوابق أخرى. مع سلسلة من النجاحات - 8 و 7 و 6 و 5 و 4 و 3 و 2 و 1 أخرى. إجمالي ، نحن في الطابق 55 مع بيضتين كاملتين وبدون محاولة. الجواب هو مجموع أول أعضاء M للتقدم الحسابي مع العضو الأول 1 والخطوة 1. f (2، m) = (m * m + m) / 2 . من الواضح أيضًا أنه تم استدعاء الوظيفة f (1، m) في كل خطوة ، ولكن هذا ليس دقيقًا بعد.

استمر بثلاث بيضات وعشر محاولات. في حالة الرمية الأولى الفاشلة ، سيتم تغطية الأرضيات المغطاة ببيضتين و 9 محاولات من الأسفل ، مما يعني أنه يجب إجراء الرمية الأولى من الأرضية f (2 ، 9) + 1. ثم ، إذا نجحت ، لدينا 3 بيضات و 9 محاولات . وللمحاولة الثانية تحتاج إلى صعود طوابق أخرى (2.8) + 1 طوابق. وهكذا ، حتى 3 بيضات و 3 محاولات باقية على اليدين. ثم حان الوقت للتشتت من خلال النظر في الحالات التي تحتوي على N = M ، عندما يكون هناك عدد من البيض مثل عدد المحاولات.


دعونا نعود إلى ص. (٣ ، ١٠). في الواقع ، في كل خطوة ، يتعلق الأمر بالمجموع f (2 ، m-1) - عدد الطوابق التي يمكن تحديدها في حالة الفشل ، الوحدات و f (3 ، m-1) - عدد الطوابق التي يمكن تحديدها في حالة النجاح. ويتضح أنه من خلال زيادة عدد البيض والمحاولات ، من غير المحتمل أن يتغير أي شيء. f (n، m) = f (n - 1، m - 1) + 1 + f (n، m - 1) . وهذه صيغة عالمية يمكن تنفيذها في التعليمات البرمجية.

from functools import lru_cache @lru_cache() def height(n,m): if n==0 or m==0: return 0 elif n==1: return m elif n==2: return (m**2+m)/2 elif n>=m: return 2**n-1 else: return height(n-1,m-1)+1+height(n,m-1) 

بالطبع ، لقد خطوت سابقًا على أشعل وظائف عودية لا تتذكرها واكتشفت أن f (10 ، 40) يستغرق 40 ثانية تقريبًا مع عدد المكالمات إلى نفسه - 97806983. لكن الحفظ أيضًا يحفظ فقط في الفترات الأولية. إذا تم تنفيذ f (200،400) في 0.8 ثانية ، فسيكون f (200 ، 500) في 31 ثانية بالفعل. من المضحك أنه عند قياس وقت التشغيل باستخدام٪ timeit ، تكون النتيجة أقل بكثير من الحقيقية. من الواضح أن التشغيل الأول للوظيفة يستغرق معظم الوقت ، بينما يستخدم الباقي ببساطة نتائج مذكرته. الأكاذيب والأكاذيب الصارخة والإحصاءات.

ليست هناك حاجة إلى العودية ، ونحن ننظر إلى أبعد من ذلك

لذا ، في الاختبارات ، على سبيل المثال ، تظهر f (9477 ، 10000) ، لكن شفقتي المثيرة للشفقة (200 ، 500) لم تعد مناسبة في الوقت المناسب. لذلك هناك حل آخر ، دون التكرار ، سنواصل البحث. لقد أكملت الشفرة عن طريق حساب استدعاءات الوظائف مع معلمات معينة من أجل معرفة ما تحلل في النهاية. للحصول على 10 محاولات ، تم الحصول على النتائج التالية:

f (3.10) = 7+ 1 * f (2.9) + 1 * f (2.8) + 1 * f (2.7) + 1 * f (2.6) + 1 * f (2 ، 5) + 1 * f (2،4) + 1 * f (2،3) + 1 * f (3،3)
f (4.10) = 27+ 1 * f (2.8) + 2 * f (2.7) + 3 * f (2.6) + 4 * f (2.5) + 5 * f (2 ، 4) + 6 * f (2،3) + 6 * f (3،3) + 1 * f (4،4)
f (5.10) = 55+ 1 * f (2.7) + 3 * f (2.6) + 6 * f (2.5) + 10 * f (2.4) + 15 * f (2 ، 3) + 15 * f (3.3) + 5 * f (4.4) + 1 * f (5.5)
f (6.10) = 69+ 1 * f (2.6) + 4 * f (2.5) + 10 * f (2.4) + 20 * f (2.3) + 20 * f (3 ، 3) + 10 * f (4.4) + 4 * f (5.5) + 1 * f (6.6)
f (7،10) = 55+ 1 * f (2،5) + 5 * f (2،4) + 15 * f (2،3) + 15 * f (3،3) + 10 * f (4 ، 4) + 6 * f (5.5) + 3 * f (6.6) + 1 * f (7.7)
f (8،10) = 27+ 1 * f (2،4) + 6 * f (2،3) + 6 * f (3،3) + 5 * f (4،4) + 4 * f (5 ، 5) + 3 * f (6.6) + 2 * f (7.7) + 1 * f (8.8)
f (9،10) = 7+ 1 * f (2،3) + 1 * f (3،3) + 1 * f (4،4) + 1 * f (5،5) + 1 * f (6 ، 6) + 1 * f (7.7) + 1 * f (8.8) + 1 * f (9.9)

بعض الانتظام مرئي:



يتم حساب هذه المعاملات نظريا. كل أزرق هو مجموع الجزء العلوي واليسار. والبنفسجي هم نفس اللون الأزرق ، فقط بالترتيب العكسي. يمكنك الحساب ، ولكن هذا هو مرة أخرى عودية ، وخاب أملي فيه. على الأرجح ، كثيرون (من المؤسف أنني لست أنا) قد تعلموا بالفعل هذه الأرقام ، ولكن في الوقت الحالي سأحتفظ بالمؤامرة ، بعد حل خاص بي. قررت أن أبصق عليهم وأن أذهب إلى الجانب الآخر.

فتح إكسل ، وبنى صفيحة بنتائج الوظيفة ، وبدأ في البحث عن الأنماط. C3 = IF (C $ 2> $ B3؛ 2 ^ $ B3-1؛ C2 + B2 + 1) ، حيث $ 2 هو الصف الذي يحتوي على عدد البيض (1-13) ، $ B هو العمود الذي يحتوي على عدد المحاولات (1-20) ، C3 - خلية عند تقاطع بيضتين ومحاولة واحدة.



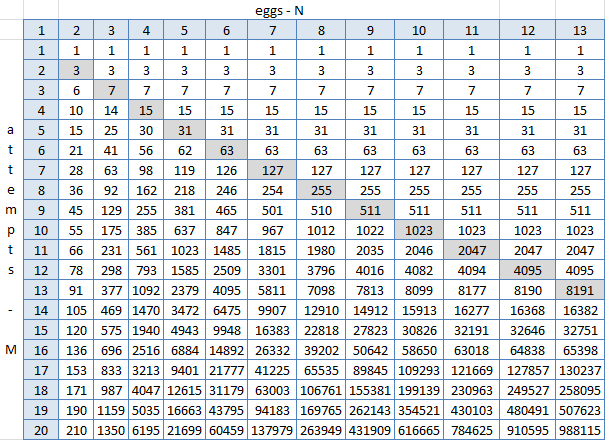
القطر الرمادي N = M ، وهنا من الواضح أنه على يمينه (N> M) لا شيء يتغير. يمكن رؤيته - ولكن لا يمكن أن يكون الأمر خلاف ذلك ، لأن هذه هي جميع نتائج عمل الصيغة ، حيث يتم إعطاء أن كل خلية تساوي مجموع القمة ، أعلى اليسار وواحدة. ولكن لم يتم العثور على بعض الصيغة العالمية حيث يمكنك استبدال N و M والحصول على رقم الطابق. المفسد: لا وجود له. ولكن من السهل إنشاء هذا الجدول في إكسيل ، ربما من الممكن إنشاء نفس الثعبان وسحب الإجابات منه؟

Numpy لا

أتذكر أن هناك NumPy ، المصمم فقط للعمل مع المصفوفات متعددة الأبعاد ، فلماذا لا تجربه؟ بادئ ذي بدء ، نحتاج إلى صفيف أحادي البعد من الأصفار بالحجم N + 1 وصفيف أحادي البعد من وحدات الحجم N. خذ الصفيف الأول من صفر إلى العنصر قبل الأخير ، وأضفه بشكل أولي مع الصفيف الأول من العنصر الأول إلى الأخير ومع صفيف من الوحدات. إلى الصفيف الناتج ، أضف صفرًا إلى البداية. كرر M مرات. سيكون العنصر رقم N للصفيف الناتج هو الجواب. تبدو الخطوات الثلاث الأولى كما يلي:



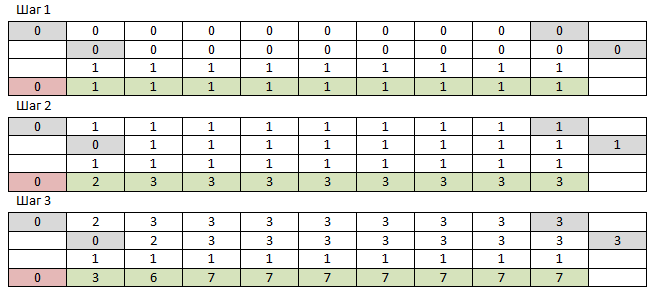
يعمل NumPy بسرعة كبيرة لدرجة أنني لم أحفظ الجدول بأكمله - في كل مرة أقرأ فيها الصف الضروري مرة أخرى. شيء واحد - كانت نتيجة العمل على أعداد كبيرة خاطئة. الرتب العليا مثل هؤلاء ، بينما الرتب الدنيا ليست كذلك. هذه هي الطريقة التي تبدو بها الأخطاء الحسابية لأرقام الفاصلة العائمة المتراكمة من إضافات متعددة. لا يهم - يمكنك تغيير نوع الصفيف إلى int. لا ، مشكلة - اتضح أنه من أجل السرعة يعمل NumPy فقط مع أنواع البيانات الخاصة به ، ولا يمكن أن يكون int الخاص به ، على عكس Python int ، أكثر من 2 ^ 64-1 ، وبعد ذلك يفيض بصمت ويستمر مع -2 ^ 64. وأتوقع بالفعل أرقامًا أقل من ثلاثة آلاف حرف. لكنه يعمل بسرعة كبيرة ، f (9477 ، 10000) يعمل بسرعة 233 مللي ثانية ، وتبين فقط نوعًا من الهراء عند الإخراج. لن أعطي الرمز حتى ، لأن مثل هذا الشيء. سأحاول أن أصنع نفس الثعبان النظيف.

متكرر ومكرر ولكن غير متكرر

 def height(n, m): arr = [0]*(n+1) while m > 0: arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) m-=1 return arr[n] 

44 ثانية لحساب f (9477 ، 10000) أكثر قليلاً. لكن بالتأكيد بالتأكيد. ما الذي يمكن تحسينه؟ أولاً ، ليست هناك حاجة للنظر في كل شيء على يمين قطري م ، م. والثاني - النظر في المصفوفة الأخيرة ككل ، من أجل خلية واحدة. لهذا ، سوف يصلح آخر خليتين من الخلية السابقة. لحساب f (10 ، 20) ، ستكون هذه الخلايا الرمادية فقط كافية:



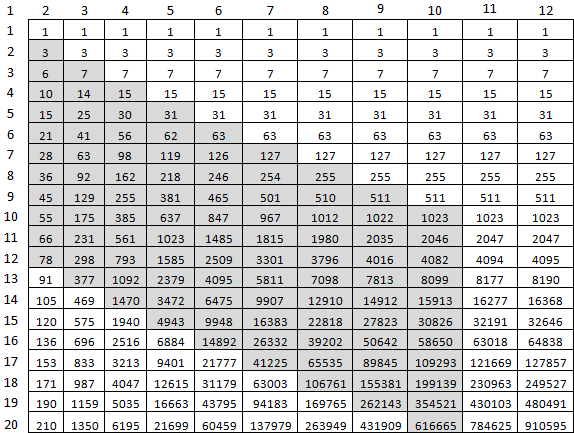
وهكذا يبدو في الكود:

 def height(n, m): arr = [0, 1, 1] i = 1 while i < n and i < mn: #    m,m arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) arr += [arr[-1]] i+=1 arr.pop(-1) while i < n or i < mn: #        arr = list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) arr = arr + [arr[-1]+1] if n > len(arr) else [0] + arr i+=1 while i < m: # ,     -  arr = list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) i+=1 return arr[0] 

وما رأيك؟ f (9477 ، 10000) في ثانيتين! لكن هذا الإدخال جيد جدًا ، لن يكون طول المصفوفة في أي مرحلة أكثر من 533 عنصرًا (10000-9477). دعونا نتحقق من ص (5477 ، 10000) - 11 ثانية. إنه جيد أيضًا ، ولكن فقط مقارنة بـ 44 ثانية - لن يمر 20 اختبارًا في هذا الوقت.

ليس الأمر كذلك. ولكن بما أن هناك مهمة ، فهناك حل ، يستمر البحث. بدأت أنظر إلى جدول Excel مرة أخرى. الخلية الموجودة على يسار (م ، م) دائمًا أقل. والخلية على يسارها لم تعد موجودة ، في كل صف يصبح الفرق أكبر. تكون الخلية أدناه (م ، م) أكبر بمرتين. والخلية الموجودة أسفلها لم تعد مرتين ، ولكنها أصغر قليلاً ، ولكن لكل عمود بشكل مختلف ، كلما كان أكبر ، كلما كان أكبر. وكذلك تنمو الأرقام في سطر واحد في البداية بسرعة ، وبعد المنتصف ببطء. اسمحوا لي أن أبني جدولاً للاختلافات بين الخلايا المجاورة ، ربما ما هو النمط الذي سيظهر هناك؟

أكثر دفئا

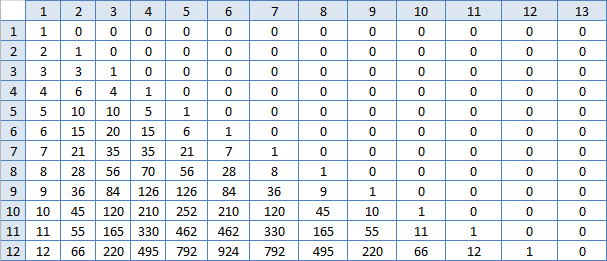
باه ، أرقام مألوفة! أي أن مجموع N من هذه الأرقام في السطر M هو هذا الجواب؟ صحيح أن عدهم هو تقريبًا نفس ما فعلته بالفعل ، فمن غير المحتمل أن يؤدي هذا إلى تسريع العمل بشكل كبير. ولكن عليك أن تجرب:



لا يعني أن الحل الأمثل. يعمل بشكل أسرع على بعض البيانات ، أبطأ على بعض. يجب أن نتعمق أكثر. ما هذا المثلث مع الأرقام التي ظهرت في الحل مرتين؟ من العار أن أعترف ، لكنني نسيت الرياضيات العليا بأمان ، حيث يجب أن يكون المثلث قد برز ، لذلك اضطررت إلى البحث عنها.

البنغو!

مثلث باسكال ، كما يطلق عليه رسميًا. جدول معامل لا حصر له. لذا فإن الإجابة على المشكلة مع بيض N ورميات M هي مجموع المعاملات N الأولى في توسع ذو الحدين نيوتن من درجة Mth ، باستثناء الصفر.

يمكن حساب معامل ذي حدين تعسفي من خلال معاملات رقم الصف ورقم المعامل في الصف: bk = m! / (N! * (Mn!)). لكن أفضل جزء هو أنه يمكنك حساب الأرقام في السلسلة بالتسلسل ، مع معرفة الرقم والمعامل الصفري (دائمًا واحد): bk [n] = bk [n-1] * (m - n + 1) / n. في كل خطوة ، ينخفض ​​البسط بمقدار واحد ، ويزيد المقام. والحل النهائي المختصر يبدو كما يلي:

 def height(n, m): h, bk = 0, 1 #      for i in range(1, n + 1): bk = bk * m // ih += bk m-=1 return h 

33 مللي ثانية لحساب f (9477 ، 10000)! يمكن أيضًا تحسين هذا الحل ، على الرغم من أنه في نطاقات معينة ويعمل بشكل جيد. إذا كانت n تقع في النصف الثاني من المثلث ، فيمكننا قلبها إلى mn ، وحساب مجموع المعاملات n الأولى وطرحها من 2 ^ m-2. إذا كان n قريبًا من الوسط وكان m فرديًا ، فيمكن أيضًا تقليل الحسابات: سيكون مجموع النصف الأول من الخط 2 ^ (m-1) -1 ، ويمكن حساب المعامل الأخير في النصف الأول من خلال العوامل ، رقمه هو (m-1) / 2 ، ثم استمر في إضافة المعاملات إذا كان n في النصف الأيمن من المثلث ، أو اطرح إذا كان في اليسار. إذا كانت m متساوية ، فلا يمكنك حساب نصف السطر ، ولكن يمكنك العثور على مجموع المعامِلات m / 2 + 1 الأولى عن طريق حساب المتوسط ​​من خلال العوامل وإضافة نصفه إلى 2 ^ (m-1) -1. على بيانات الإدخال في منطقة 10 ^ 6 ، يقلل هذا بشكل ملحوظ من وقت التنفيذ.

بعد قرار ناجح ، بدأت في البحث عن بحث شخص آخر حول هذه المسألة ، لكنني وجدت نفس الشيء فقط ، من المقابلات ، مع بيضتين فقط ، وهذه ليست رياضة. قررت أن الإنترنت لن تكتمل بدون قراري ، وهنا.