جوليا. التعارف

قصيدة لجوليا

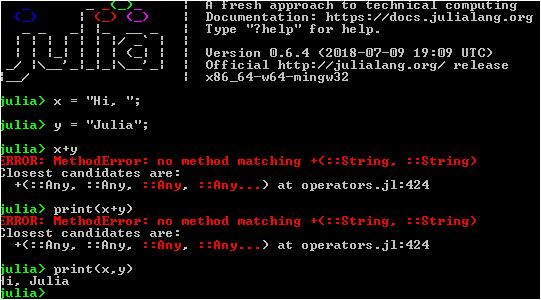
من الصعب جدًا التعبير عن كل الحماس الذي صاحب إطلاق البرامج الأولى وتصحيح الأخطاء الأولى باستخدام هذه اللغة. بسيطة وجميلة مثل Python ، تشبه إلى حد ما فورتران ، العمل المريح مع المصفوفات والرسوم البيانية ، بالإضافة إلى القدرة على أداء التحسين والتوازي الشرس حتى بالنسبة للدمى مثل ط زملائي. يمكنك العمل على مستويات مختلفة من التجريد: من البرمجة عالية المستوى مع الكتابة الديناميكية ، يمكنك الانتقال إلى أوامر التجميع ، أي هنا لديك إمكانية الوصول إلى Python وسرعة تنفيذ عدادات Fortran. لا يمكنني التخلص من الشعور بأن Mathcad و Scilab وحتى الله يغفر لي ، C ++ بدأت في التلاشي في قلبي.

تعلمت اللغة عن طريق التعثر عن طريق الخطأ في منشور خابروفي ، وكما يجب على الطالب الذي تأثرت به ، بدأت في البحث عن التوجيه ، ويفضل أن يكون ذلك باللغة الروسية. نظرًا لأن اللغة كانت تتطور باستمرار لمدة ست سنوات ، أصبحت مصادر المعلومات النادرة بالفعل عفا عليها الزمن ، وبدأ الإثارة في الانخفاض. ولكن مع بداية دورة مختبرية جديدة حول نمذجة الظواهر الفيزيائية مع حرية اختيار لغة البرمجة ، كان لا يزال هناك دافع لبدء التعرف على جوليا. بالإضافة إلى ذلك ، في أغسطس ، لغة "إضافة 1.0" .

تم تخطيط المواد الواردة أدناه كمقدمة للغة التي كُتبت بها جميع الأوراق المعملية وجمع دليل التدريب.

جوليا هي لغة برمجة ديناميكية عالية المستوى وعالية الأداء للحسابات الحسابية. الصيغة مشابهة لعائلة matlab ، اللغة مكتوبة في C و C ++ و Scheme ، من الممكن استدعاء مكتبات Sysh

التثبيت

حسنًا ، استقر كل شيء أخيرًا ، الآن تحت تصرفنا:

• موجه أوامر JuliaPRO - جميع مهارات Yulina مباشرة من المترجم.
• Juno هو بيئة تطوير متكاملة جميلة مع نافذة للرسوم البيانية ومساحة عمل حيث يمكنك عرض محتويات جميع الكائنات
• Jupyter - تطلق جوهر الحوسبة في وحدة التحكم ، ويمكنك تنفيذ التعليمات البرمجية مباشرة في المتصفح. (بالإضافة إلى جوليا ، Python موجودة أيضًا)

دعونا نرى ما يمكن أن تفعله هذه الآلة الحاسبة ... دعم Unicode - يمكنك استخدام الأبجدية السيريلية والهيروغليفية واستدعاء pi بالحرف اليوناني. ولا يمكنك تحديد الضرب بشكل صريح بين الرقم والمتغير (بهذا الترتيب وبدون مسافة):

x = 5+8 2x - 3x + 2x^2 Out: 325 

جميع العلامات اللازمة موجودة أيضًا: + = ، * = ، >> = ، إلخ. (علامة ">>" (تحول البت إلى اليمين). علامات المقارنة:> ،> = ، <، <= ، == ،! =. يمكن دمج عدم المساواة في سلاسل:

 y = 5 y += 2 4 <= y < 8 Out: true 

الأعداد المركبة المتاحة:

 (2-1im)*(4+3im) Out: 11 + 2im 

ووظائف العمل معهم:

• الحقيقي (ض) هو الجزء الحقيقي ،
• imag (z) هو الجزء التخيلي ،
• conj (z) هو اتحاد معقد ،
• عبس (ض) - وحدة ،
• abs2 (z) هو مربع الوحدة ،
• الزاوية (ع) هي حجة العدد المركب.

يمكنك استخدام أرقام منطقية باستخدام "//" والوظائف المقابلة:

• num (x) - البسط ،
• den (x) - المقام ،
• تعويم (س) - يتحول إلى عشري

 x = 4//6+5//7 Out: 29//21 float(x) Out: 1.380952380952381 

تمتلك جوليا القدرة على التحكم في التمثيل الداخلي للبيانات:

• typeof (obj) - نوع الكائن
• typemax (obj) هو أقصى عدد من هذا النوع
• typemin (obj) - الحد الأدنى
• eps () - الجهاز صفر
• BigInt هو كل كبير
• BigFloat - نقطة عائمة كبيرة

 q = 3 typemax(q) Out: 9223372036854775807 typeof(q) Out: Int64 BigFloat(2.3^45/6) Out: 3.159376405019356000000000000000000000000000000000000000000000000000000000000e+15 

وظائف

مجموعة الميزات

• القيمة المطلقة (x) هي معامل العدد ،
• abs2 (x) هو مربع الوحدة ،
• sqrt (x) هو الجذر التربيعي ،
• cbrt (x) هو الجذر التكعيبي ،
• exp (x) هو أس العدد ،
• log (x) هو اللوغاريتم الطبيعي ،
• log10 (x) - اللوغاريتم العشري ،
• log (b، x) هو لوغاريتم x في الأساس b.
  بالإضافة إلى المثلثات ، الزائدية ، التهوية ، Bessel وغيرها الكثير.

وظائف مخصصة:

 function () #  end 

تقوم الدالة بإرجاع نتيجة التعبير الأخير (مستخدم Mathcad hiccuped).

 function cube(x) x^3 end cube(4) Out: 64 

حسنًا ، أو نشير بشكل صريح إلى:

 function myabs(x) if x>=0 return x else return -x end end myabs(-12) Out: 12 

يمكن جمع القيم المرتجعة في مجموعة:

 function cubeandsquare(x) x^3,x^2 end a,b = cubeandsquare(3) print("a = $a, b = $b") Out: a = 27, b = 9 

يمكن أن تأخذ الوظائف الصفوف والقيم الافتراضية والكلمات الرئيسية. إذا لم تكن هناك أقواس بعد اسم الوظيفة ، فسيتم اعتبارها متغيرًا ويمكن تعيينها لمتغير آخر أو نقلها إلى الدالة كمعلمة. تدعم جوليا أيضًا النمط الوظيفي لبرامج الكتابة (hello Lisp)

 function mysin(t;A=1,?=1,?=0) #   -     A*sin(?*t + ?) end x1 = mysin(pi) #   = 0 x2 = mysin(pi*0.5,A = 2) #      x3 = mysin(pi*0.5,? = 0.5) #      print("x1 = $x1, x2 = $x2, x3 = $x3") Out: x1 = 1.2246467991473532e-16, x2 = 2.0, x3 = 0.7071067811865475 

المصفوفات

كمستخدم Scilab ، لم ألاحظ حتى الاستبدال: يمكنك تحديد مصفوفة باستخدام الوظيفة:

• Array {T} (undef، dims ...) - صفيف من النوع T و dims بعد
• الأصفار (T ، dims ...) - صفيف من الأصفار
• تلك (T ، dims ...) - أو الوحدات
  تبدأ الفهرسة بواحدة ، بدلاً من $ - end ، ويتم تحديد جميع العمليات اللازمة للمصفوفات (من أجل إجراء ، على سبيل المثال ، إضافة أو ضرب عنصر ، تحتاج إلى وضع نقطة أمام عامل التشغيل).

(الآن أصبح من الواضح كيفية إدراج الصور ، ولكن حسنًا ...)

الوظائف الأساسية:

• det (A) - احسب المحدد
• أ ' - تبديل المصفوفة
• inv (A) - مصفوفة معكوسة
• الطول (أ) - عدد العناصر
• ndims (A) - عدد الأبعاد
• الحجم (أ) - عدد الأبعاد
• الحجم (أ ، ن) - البعد في اتجاه معين
• نسخة (أ) - إنشاء نسخة من الصفيف
• linspace (بداية ، نهاية ، خطوة) أو
  linspace (start: step: end) - إنشاء صفيف أحادي البعد

 A = [1 2 3; 6 5 4; 7 8 9] Out: 3?3 Array{Int64,2}: 1 2 3 6 5 4 7 8 9 A[2,1] Out: 6 A[end] Out: 9 size(A) Out: (3, 3) 

يمكنك تحديد أجزاء من الصفيف عن طريق تحديد مجموعة من المؤشرات على طول البعد مع علامة ":".

 m1 = rand(3,2) m2 = reshape(1:2:11, 3,2) Out: 3?2 Base.ReshapedArray{Int64,2,StepRange{Int64,Int64},Tuple{}}: 1 7 3 9 5 11 m3 = [m1 m2] #   (  ) Out: 3?4 Array{Float64,2}: 0.325649 0.701038 1.0 7.0 0.513579 0.620215 3.0 9.0 0.815242 0.805307 5.0 11.0 m5 = [m1; m2] #   (  ) Out: 6?2 Array{Float64,2}: 0.325649 0.701038 0.513579 0.620215 0.815242 0.805307 1.0 7.0 3.0 9.0 5.0 11.0 m3[:, 2:4] Out: 3?3 Array{Float64,2}: 0.701038 1.0 7.0 0.620215 3.0 9.0 0.805307 5.0 11.0 

استخدمنا هنا rand () ، الذي يُرجع مصفوفة من الأرقام العشوائية لبُعد معين ، ويعيد تشكيل () ، الذي يغير بُعد المصفوفة إلى البعد المحدد.

 for a in A #   a   A end 

أو

 for i in eachindex(A) #     i end 

أو

 for i = 1 : size(A,n) # n -      (..    ) #     i end 

الرسوم البيانية

لاستخدام الرسومات ، تحتاج إلى تنزيل حزمة من المستودع للاختيار من بينها:

• Pkg.add ("قطع الأرض")
• Pkg.add ("PyPlot")
• Pkg.add ("Gadfly")
• Pkg.add ("Winston")

الأكثر شعبية هو Pythonic PyPlot . الوحدات متصلة باستخدام الأمر ، على سبيل المثال:

 using PyPlot 

ومع ذلك ، دعنا نجرب Gaston باستخدام Gnuplot (تأرجح بشكل منفصل).
تم تحميله بواسطة فريق Gaston.jl

  Pkg.add("Gaston") 

والحق في النقطة:

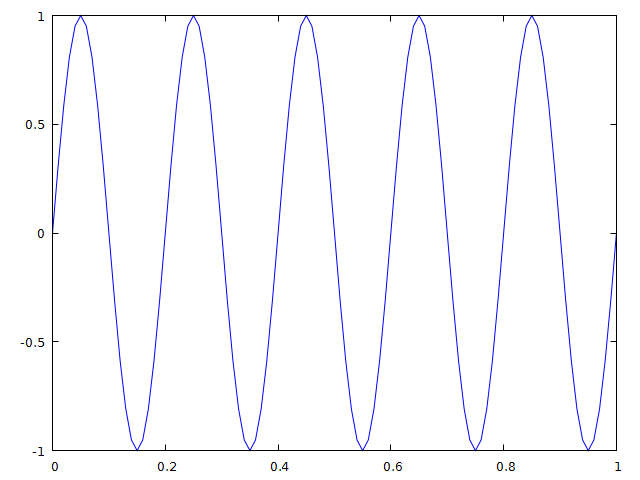
 using Gaston t = 0:0.01:1 plot(t, sin.(2?*5*t)) 

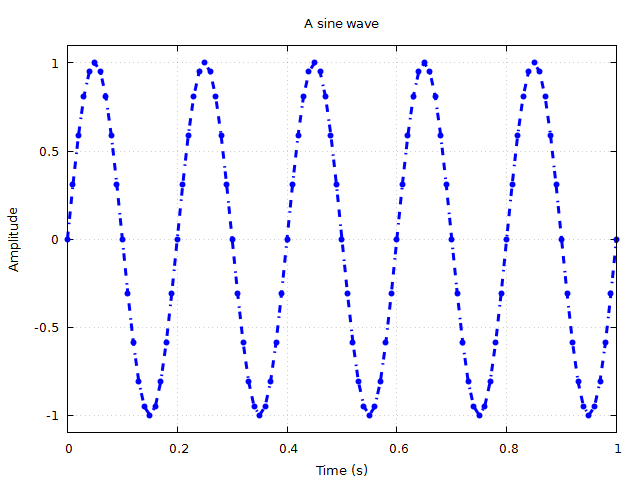
 plot(t,sin.(2?*5*t),title="A sine wave",xlabel="Time (s)",ylabel="Amplitude",grid="on",linewidth=3,color="blue", yrange="[-1.1:1.1]",marker="ecircle",plotstyle="linespoints",linestyle="-.-") 

 plot!(t,cos.(2?*5*t),color="red",linewidth=2) #       

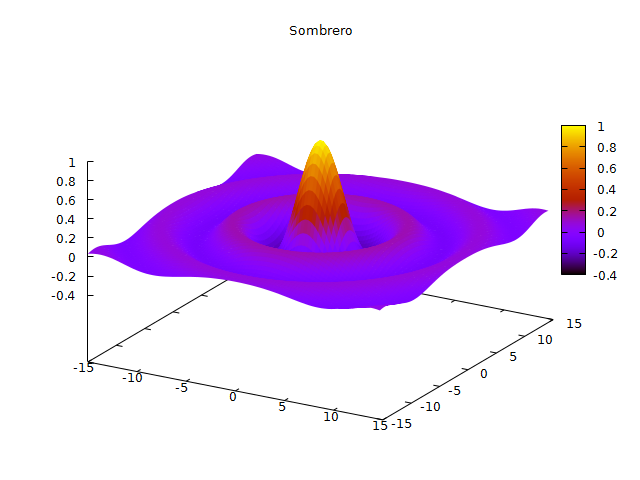
 x = y = -15:0.33:15 surf(x,y,(x,y)->sin.(sqrt.(x.*x+y.*y))./sqrt.(x.*x+y.*y),title="Sombrero",plotstyle="pm3d") 

 x = y = -15:0.33:15 surf(x,y,(x,y)->sin.(sqrt(x.*x+y.*y))./sqrt.(x.*x+y.*y), title="Edge view of a sombrero",plotstyle="pm3d",gpcom="set view 80,20") 

 R = [ x+y for x=0:5:120, y=0:5:120] G = [ x+y for x=0:5:120, y=120:-5:0] B = [ x+y for x=120:-5:0, y=0:5:120] Z = zeros(25,25,3) Z[:,:,1] = R Z[:,:,2] = G Z[:,:,3] = B imagesc(Z,title="RGB Image",clim=[10 200]) 

 histogram(rand(1000),bins=15,norm=1,title="Histogram",yrange="[0:1.6]") 

 y = 1:40 err = Gaston.ErrorCoords(rand(40)) plot(y,err=err,title="Example of error bars",plotstyle="errorbars") 

يمكنك إنشاء نوافذ رسومية متعددة (لا تعمل في Jupyter ) باستخدام الأمر h = figure () (فقط أدخل بين المؤامرات). لحفظ الرسم البياني كملف صورة ، استخدم الأوامر
set_filename ("name.png") # إذا لم يكن محددًا ، فسيتم عرضه
printfigure ("png") # save to file، PNG، PDF، SVG and GIF available
المزيد من معلومات حزمة جاستون

الخلاصة

هناك العديد من الحزم الرسومية لكل ذوق وتغطي جميع الاحتياجات تقريبًا. أيضا ، تتطور الحزم الإضافية بقوة وقدرة. هنا لديك الحوسبة الكمومية والمعلوماتية الحيوية ، والتعلم الآلي ، والعديد من المشاكل الملحة مثل الاختلافات والمشتقات .

بشكل عام ، جوليا جميلة وذكية واعدة للغاية ، ومن غير المقبول للغاية تركها دون الاهتمام اللازم.