برمجة ديناميكية أو فرق تسد

تناقش هذه المقالة أوجه التشابه والاختلاف بين النهجين لحل مشاكل الخوارزمية: البرمجة الديناميكية (البرمجة الديناميكية) ومبدأ "فرق تسد" (فرق ​​تسد). سنقارن باستخدام خوارزميتين كمثال: البحث الثنائي (كيفية العثور بسرعة على رقم في مصفوفة مرتبة) ومسافة Levenshtein (كيفية تحويل صف إلى آخر بأقل عدد من العمليات).

أريد أن ألاحظ على الفور أن هذه المقارنة والشرح لا تدعي أنها صحيحة للغاية. وربما يرغب بعض أساتذة الجامعات في طردني :) هذه المقالة هي مجرد محاولتي الشخصية لفرز الأشياء وفهم ماهية البرمجة الديناميكية وكيف ينطوي مبدأ "فرق تسد".

لذا ، دعنا نبدأ ...

المشكلة

عندما بدأت بدراسة الخوارزميات ، كان من الصعب بالنسبة لي أن أفهم الفكرة الأساسية للبرمجة الديناميكية (المشار إليها فيما يلي باسم DP ، من البرمجة الديناميكية) وكيف تختلف عن نهج "فرق تسد" (مزيد من العاصمة ، من فرق تسد). عندما يتعلق الأمر بمقارنة هذين النموذجين ، غالبًا ما يستخدم العديد منهم بنجاح وظيفة فيبوناتشي للتوضيح. وهذا توضيح رائع. ولكن يبدو لي أنه عندما نستخدم نفس المهمة لتوضيح DP و DC ، نفقد تفاصيل مهمة واحدة يمكن أن تساعدنا على اكتشاف الفرق بين النهجين بشكل أسرع. وهذه التفاصيل هي أن هاتين التقنيتين تتجلى بشكل أفضل في حل أنواع مختلفة من المشاكل.

ما زلت في طور تعلم DP و DC ولا أستطيع أن أقول إنني فهمت تمامًا هذه المفاهيم. لكنني ما زلت آمل أن يلقي هذا المقال ضوءًا إضافيًا ويساعد على اتخاذ الخطوة التالية في دراسة مناهج مهمة مثل البرمجة الديناميكية والفرق والقهر.

التشابه بين موانئ دبي والعاصمة

بالطريقة التي أرى بها هذين المفهومين الآن ، يمكنني أن أستنتج أن موانئ دبي هي نسخة موسعة من العاصمة .

لن أعتبرهم شيئًا مختلفًا تمامًا. لأن هذين المفهومين يقسمان المشكلة بشكل متكرر إلى مشكلتين فرعيتين أو أكثر من نفس النوع حتى تكون هذه المشاكل الفرعية سهلة بما يكفي لحلها مباشرة. علاوة على ذلك ، يتم دمج جميع حلول المشكلة الفرعية معًا من أجل إعطاء إجابة في النهاية للمشكلة الأصلية الأصلية.

إذن ، لماذا لا يزال لدينا نهجان مختلفان (DP و DC) ولماذا دعوت البرمجة الديناميكية امتدادًا. هذا لأنه يمكن تطبيق البرمجة الديناميكية على المهام التي لها خصائص وقيود معينة. وفقط في هذه الحالة توسع موانئ دبي العاصمة من خلال طريقتين: الحفظ والتجميع .

دعونا نتعمق قليلاً في التفاصيل ...

القيود والخصائص اللازمة للبرمجة الديناميكية

كما اكتشفنا للتو ، هناك صفتان رئيسيتان يجب أن تمتلكهما المهمة / المشكلة حتى نحاول حلها باستخدام البرمجة الديناميكية:

1. البنية التحتية المثلى - يجب أن يكون من الممكن تكوين حل مثالي لمشكلة من الحل الأمثل لمهامه الفرعية.
2. تقاطع المشاكل الفرعية - يجب تقسيم المشكلة إلى مشاكل فرعية ، والتي بدورها يتم إعادة استخدامها بشكل متكرر. وبعبارة أخرى ، فإن النهج التعاودي لحل المشكلة ينطوي على حل متعدد ( وليس حل واحد) لنفس المشكلة الفرعية ، بدلاً من إنتاج مشاكل فرعية جديدة وفريدة في كل دورة تعاودية.

بمجرد أن نجد هاتين الخاصيتين في المشكلة التي ندرسها ، يمكننا القول أنه يمكن حلها باستخدام البرمجة الديناميكية.

البرمجة الديناميكية كامتداد لمبدأ "فرق تسد"

موانئ دبي تمتد إلى العاصمة بمساعدة تقنيتين ( الاستدلال والجدولة ) ، والغرض منها هو حفظ الحلول للمشاكل الفرعية لإعادة استخدامها في المستقبل. وبالتالي ، يتم تخزين الحلول مؤقتًا بواسطة مشكلة فرعية ، مما يؤدي إلى تحسن كبير في أداء الخوارزمية. على سبيل المثال ، التعقيد الزمني للتنفيذ التكراري "الساذج" لوظيفة فيبوناتشي هو O(2 n ) . في نفس الوقت ، يتم تنفيذ حل يعتمد على البرمجة الديناميكية في وقت (n) .

يعد Memoization (ملء ذاكرة التخزين المؤقت من الأعلى إلى الأسفل) تقنية تخزين مؤقت تستخدم حلولًا محسوبة حديثًا للمهام الفرعية. تبدو وظيفة فيبوناتشي باستخدام تقنية الحفظ كما يلي:

 memFib(n) { if (mem[n] is undefined) if (n < 2) result = n else result = memFib(n-2) + memFib(n-1) mem[n] = result return mem[n] } 

يعد الجدولة (ملء ذاكرة التخزين المؤقت من الأسفل إلى الأعلى) أسلوبًا مشابهًا ، ولكنه يركز بشكل أساسي على ملء ذاكرة التخزين المؤقت ، وليس على إيجاد حل للمشكلة الفرعية. حساب القيم التي تحتاج إلى التخزين المؤقت أسهل في هذه الحالة ليتم تنفيذها بشكل متكرر ، وليس بشكل متكرر. تبدو دالة فيبوناتشي باستخدام تقنية الجدولة كما يلي:

 tabFib(n) { mem[0] = 0 mem[1] = 1 for i = 2...n mem[i] = mem[i-2] + mem[i-1] return mem[n] } 

يمكنك قراءة المزيد حول المقارنة بين المذكرات والجدولة هنا .

الفكرة الرئيسية التي يجب أن تُدرس في هذه الأمثلة هي أنه نظرًا لأن مشاكل التيار المستمر الخاصة بنا تحتوي على مشاكل فرعية متداخلة ، يمكننا استخدام التخزين المؤقت لحلول المشكلات الفرعية باستخدام إحدى طريقتين للتخزين المؤقت: الحفظ والتجميع.

فما الفرق بين موانئ دبي والعاصمة في النهاية

تعلمنا عن القيود والمتطلبات المسبقة لاستخدام البرمجة الديناميكية ، وكذلك تقنيات التخزين المؤقت المستخدمة في نهج DP. لنحاول تلخيص وتصوير الأفكار المذكورة أعلاه في الرسم التوضيحي التالي:



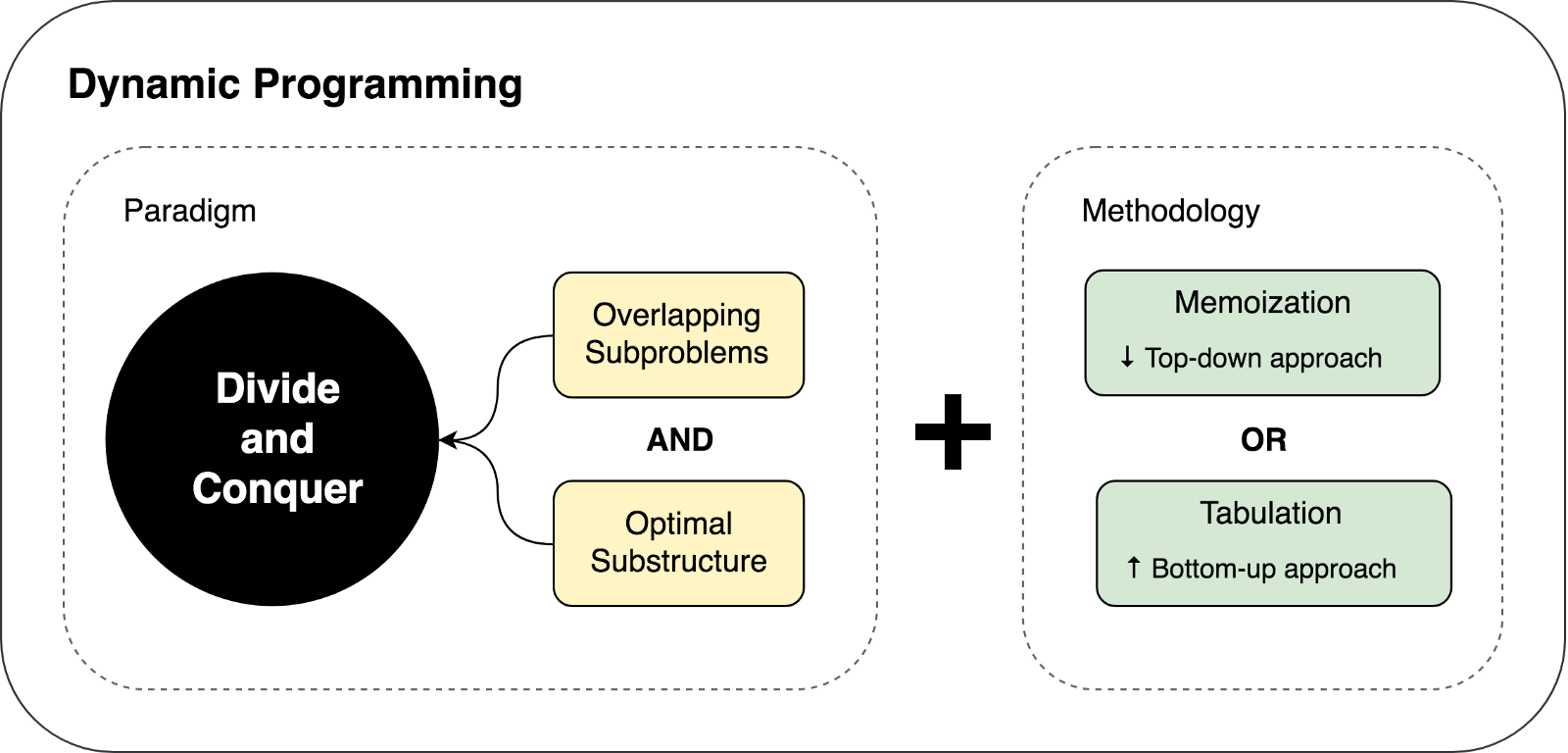
دعونا نحاول حل مشكلتين باستخدام DP و DC لإثبات كل من هذه الأساليب في العمل.

مثال Divide and Conquer: بحث ثنائي

خوارزمية البحث الثنائي هي خوارزمية بحث تعثر على موضع العنصر المطلوب في صفيف مفروز. في البحث الثنائي ، نقارن قيمة المتغير مع قيمة العنصر في منتصف المصفوفة. إذا لم تكن متساوية ، فإن نصف الصفيف الذي لا يمكن فيه استبعاد العنصر المطلوب من البحث الإضافي. يستمر البحث في هذا النصف من المصفوفة ، حيث يمكن تحديد المتغير المطلوب حتى يتم العثور عليه. إذا كان النصف التالي من المصفوفة لا يحتوي على عناصر ، فإن البحث يعتبر مكتملاً ونستنتج أن المصفوفة لا تحتوي على القيمة المطلوبة.

مثال

الرسم التوضيحي أدناه هو مثال للبحث الثنائي عن الرقم 4 في مصفوفة.



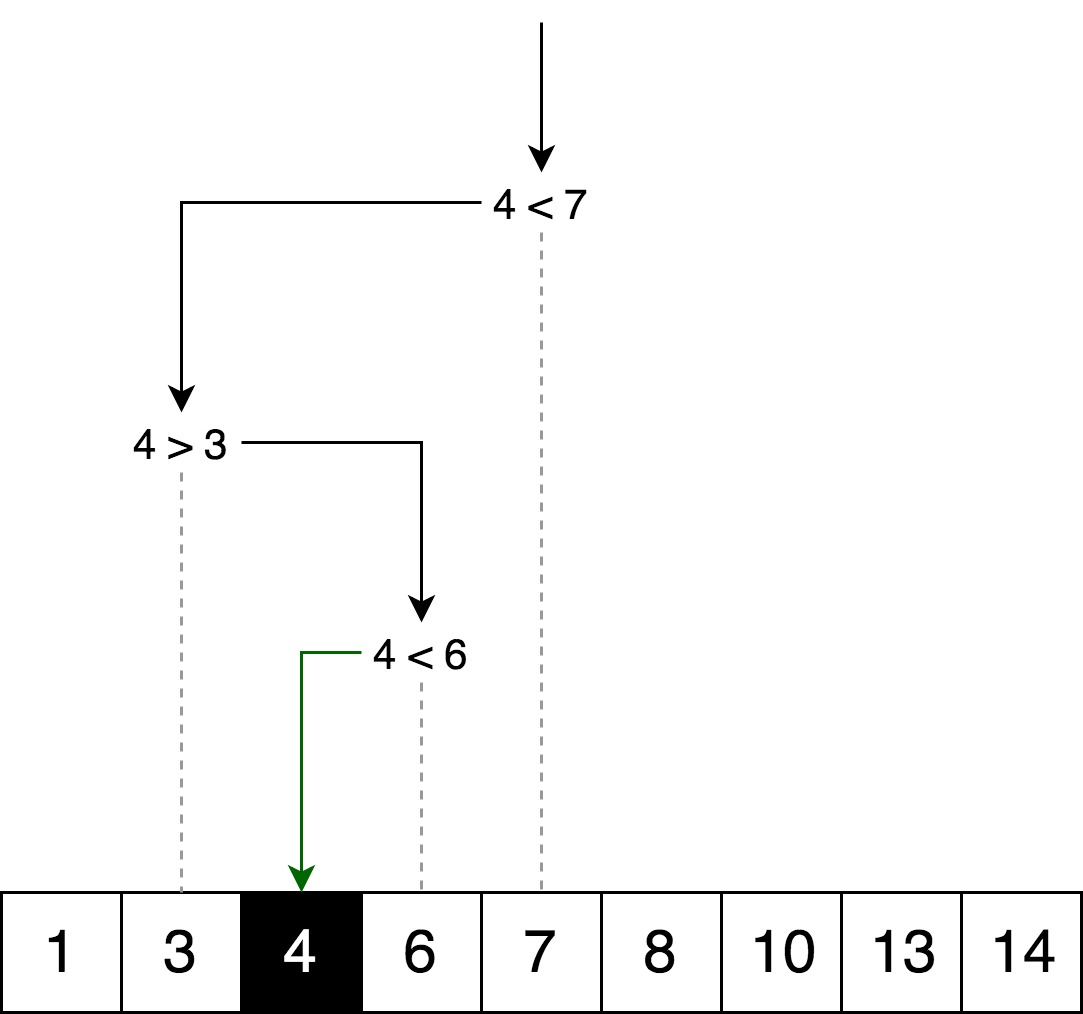
لنرسم نفس منطق البحث ، ولكن في شكل "شجرة قرارات".



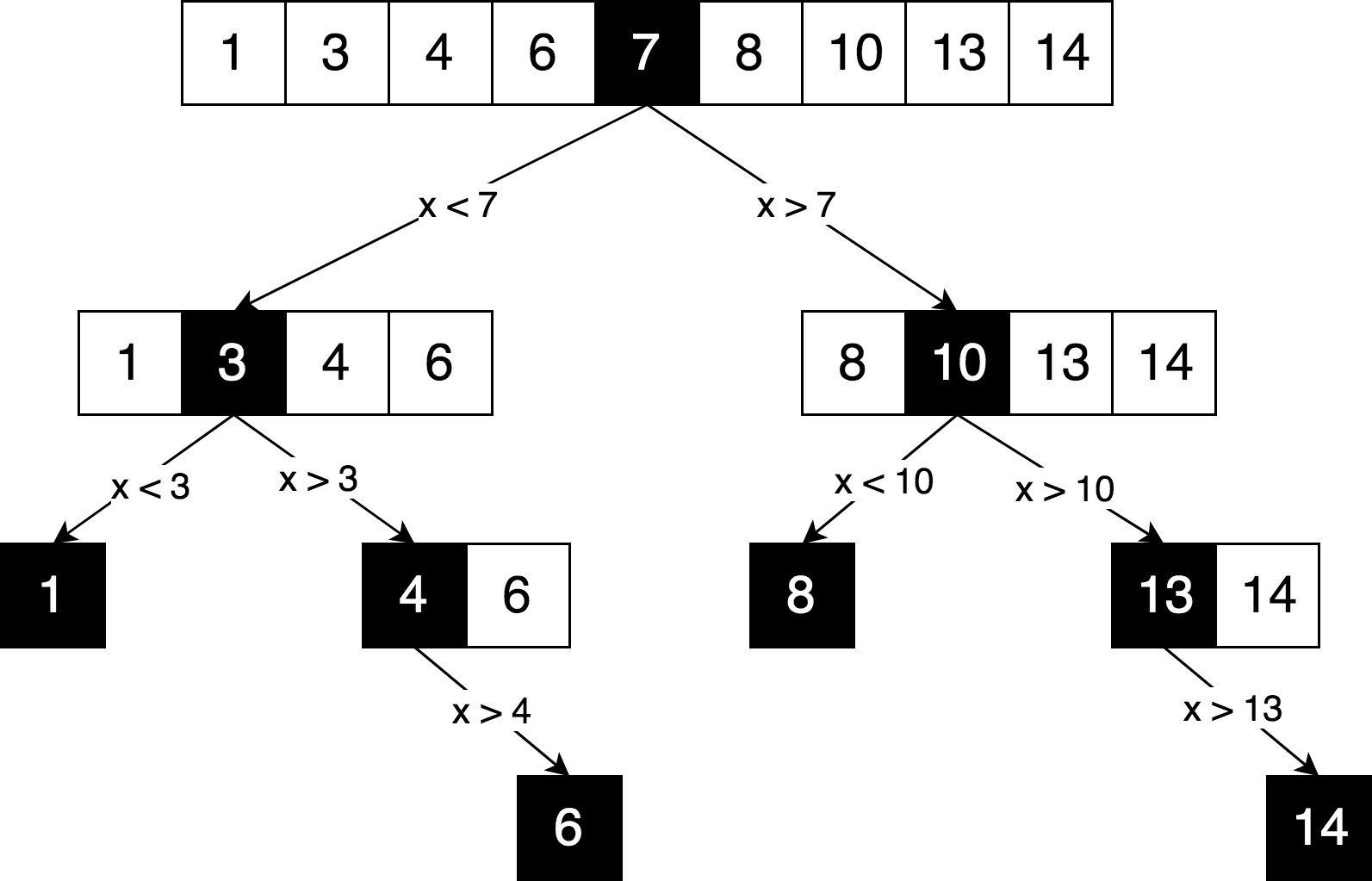
يمكنك أن ترى في هذا الرسم البياني مبدأ واضحًا لـ "فرق تسد" يستخدم لحل هذه المشكلة. قمنا بتقسيم مجموعتنا الأصلية بشكل متكرر إلى مصفوفات فرعية ونحاول العثور على العنصر الذي نبحث عنه بالفعل.

هل يمكننا حل هذه المشكلة باستخدام البرمجة الديناميكية؟ لا. لسبب أن هذه المهمة لا تحتوي على مشاكل فرعية متقاطعة . في كل مرة نقوم بتقسيم مصفوفة إلى أجزاء ، يكون كلا الجزئين مستقلين تمامًا ولا يتداخلان. ووفقًا للافتراضات والقيود على البرمجة الديناميكية التي ناقشناها أعلاه ، يجب أن تتداخل المشكلات الفرعية بطريقة أو بأخرى ، ويجب أن تكون متكررة .

عادة ، عندما تبدو شجرة القرار تمامًا مثل شجرة ( وليست مثل الرسم البياني ) ، هذا على الأرجح يعني عدم وجود مشاكل فرعية متداخلة ،

تنفيذ الخوارزمية

هنا يمكنك العثور على شفرة المصدر الكاملة لخوارزمية البحث الثنائي مع الاختبارات والتفسيرات.

 function binarySearch(sortedArray, seekElement) { let startIndex = 0; let endIndex = sortedArray.length - 1; while (startIndex <= endIndex) { const middleIndex = startIndex + Math.floor((endIndex - startIndex) / 2); // If we've found the element just return its position. if (sortedArray[middleIndex] === seekElement)) { return middleIndex; } // Decide which half to choose: left or right one. if (sortedArray[middleIndex] < seekElement)) { // Go to the right half of the array. startIndex = middleIndex + 1; } else { // Go to the left half of the array. endIndex = middleIndex - 1; } } return -1; } 

مثال البرمجة الديناميكية: تحرير المسافة

عادة ، عندما يتعلق الأمر بشرح البرمجة الديناميكية ، يتم استخدام وظيفة فيبوناتشي كمثال. ولكن في حالتنا ، لنأخذ مثالًا أكثر تعقيدًا قليلاً. كلما زادت الأمثلة ، كان من الأسهل فهم المفهوم.

مسافة التحرير (أو مسافة Levenshtein) بين سطرين هي الحد الأدنى من العمليات لإدراج حرف واحد ، وحذف حرف واستبدال حرف بأخرى ، وهو ضروري لتحويل سطر إلى آخر.

مثال

على سبيل المثال ، مسافة التحرير بين الكلمتين "kitten" و "جلسة الجلوس" هي 3 ، لأنك تحتاج إلى إجراء ثلاث عمليات تحرير (استبدالان وإدخال واحد) من أجل تحويل سطر إلى آخر. ومن المستحيل العثور على خيار تحويل أسرع مع عدد أقل من العمليات:

1. هريرة → هريرة (استبدال "k" بـ "s")
2. مكتوب → sittin (استبدال "e" بـ "i")
3. الجلوس ← الجلوس (أدخل "g" بالكامل).

تطبيق الخوارزمية

تحتوي الخوارزمية على مجموعة واسعة من التطبيقات ، على سبيل المثال ، للتدقيق الإملائي ، وأنظمة تصحيح التعرف الضوئي ، والبحث غير الدقيق للسلسلة ، وما إلى ذلك.

تعريف رياضي لمشكلة

رياضيا ، يتم تحديد مسافة ليفنشتاين بين سطرين a, b (بأطوال | أ | و |b| على التوالي) من خلال دالة function lev(|a|, |b|) ، حيث:



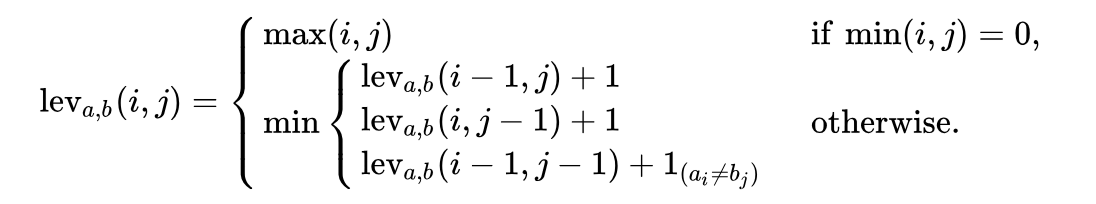
يرجى ملاحظة أن السطر الأول في دالة min يتوافق مع عملية الحذف ، والخط الثاني يتوافق مع عملية الإدراج والخط الثالث يتوافق مع عملية الاستبدال (في حالة عدم تساوي الحروف).

شرح

دعونا نحاول معرفة ما تخبرنا به هذه الصيغة. خذ مثالًا بسيطًا لإيجاد الحد الأدنى لمسافة التحرير بين خطي ME و MY . بشكل بديهي ، أنت تعرف بالفعل أن الحد الأدنى لمسافة التحرير هو عملية استبدال واحدة ( 1 ) (استبدل "E" بـ "Y"). ولكن دعونا إضفاء الطابع الرسمي على حلنا وتحويله إلى شكل خوارزمي ، حتى نتمكن من حل إصدارات أكثر تعقيدًا لهذه المشكلة ، مثل تحويل كلمة السبت إلى الأحد .

من أجل تطبيق الصيغة على التحول ME → MY ، يجب أولاً معرفة الحد الأدنى لمسافة التحرير بين ME → M و M → MY و M → M. بعد ذلك ، يجب أن نختار على الأقل ثلاث مسافات ونضيف إليها عملية واحدة (+1) للتحويل E → Y.

لذا ، يمكننا بالفعل رؤية الطبيعة العودية لهذا الحل: يتم حساب الحد الأدنى لمسافة التحرير → → MY استنادًا إلى التحولات الثلاثة المحتملة السابقة. وبالتالي ، يمكننا القول بالفعل أن هذه خوارزمية فرق تسد.

لتوضيح الخوارزمية ، دعنا نضع صفينا في مصفوفة:



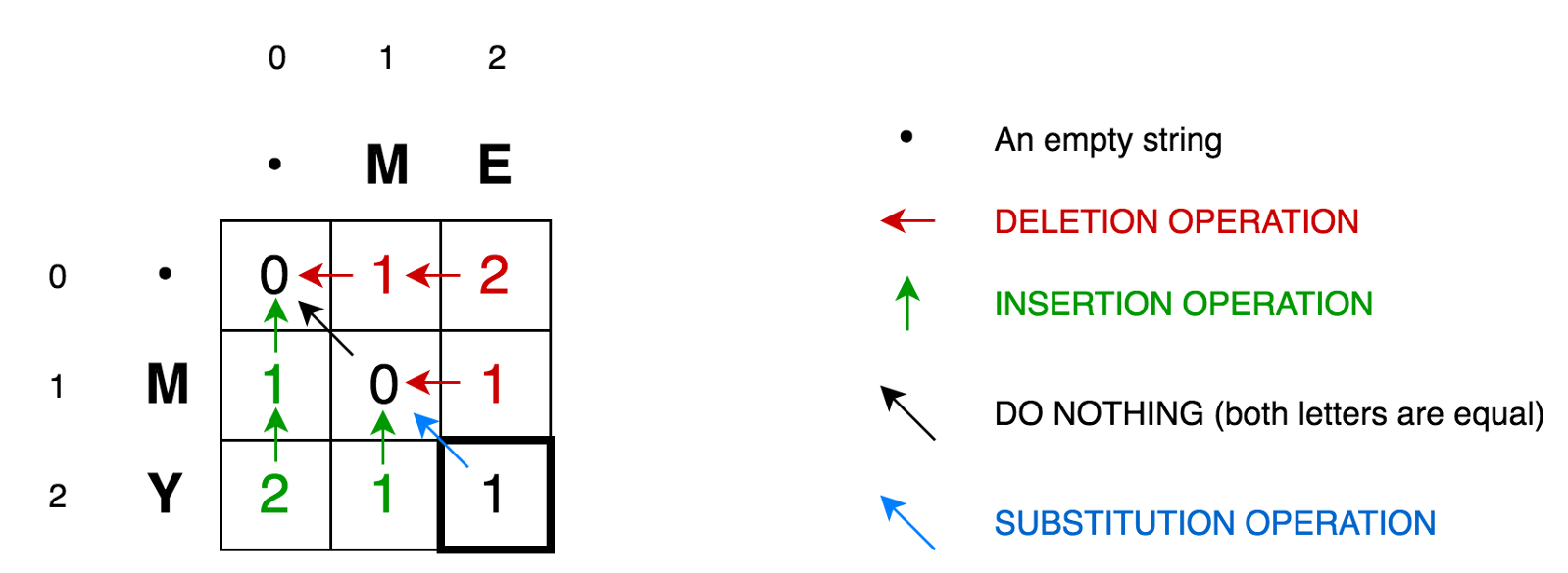تحتوي الخلية (0،1) على الرقم الأحمر 1. وهذا يعني أننا بحاجة إلى إجراء عملية واحدة لتحويل M إلى سلسلة فارغة - حذف M. لذلك ، قمنا بتمييز هذا الرقم باللون الأحمر.

تحتوي الخلية (0،2) على رقم أحمر 2. وهذا يعني أننا بحاجة إلى إجراء عمليتين من أجل تحويل السلسلة ME إلى سلسلة فارغة - حذف E ، حذف M.

تحتوي الخلية (1،0) على رقم أخضر 1. وهذا يعني أننا بحاجة إلى عملية واحدة لتحويل سلسلة فارغة إلى M - لصق M. وقد قمنا بوضع علامة على عملية الإدراج باللون الأخضر.

تحتوي الخلية (2،0) على رقم أخضر 2. هذا يعني أننا بحاجة إلى إجراء عمليتين لتحويل سلسلة فارغة إلى سلسلة MY - insert Y، insert M.

تحتوي الخلية (1،1) على الرقم 0. وهذا يعني أننا لسنا بحاجة إلى القيام بأي عمليات لتحويل السلسلة M إلى M.

تحتوي الخلية (1،2) على الرقم الأحمر 1. وهذا يعني أننا بحاجة إلى إجراء عملية واحدة لتحويل السلسلة ME إلى M - حذف E.

وهكذا ...

لا يبدو الأمر صعبًا بالنسبة للمصفوفات الصغيرة ، مثل المصفوفات (3 × 3 فقط). ولكن كيف يمكننا حساب قيم جميع الخلايا للمصفوفات الكبيرة (على سبيل المثال ، لمصفوفة 9x7 في التحول يوم السبت → الأحد)؟

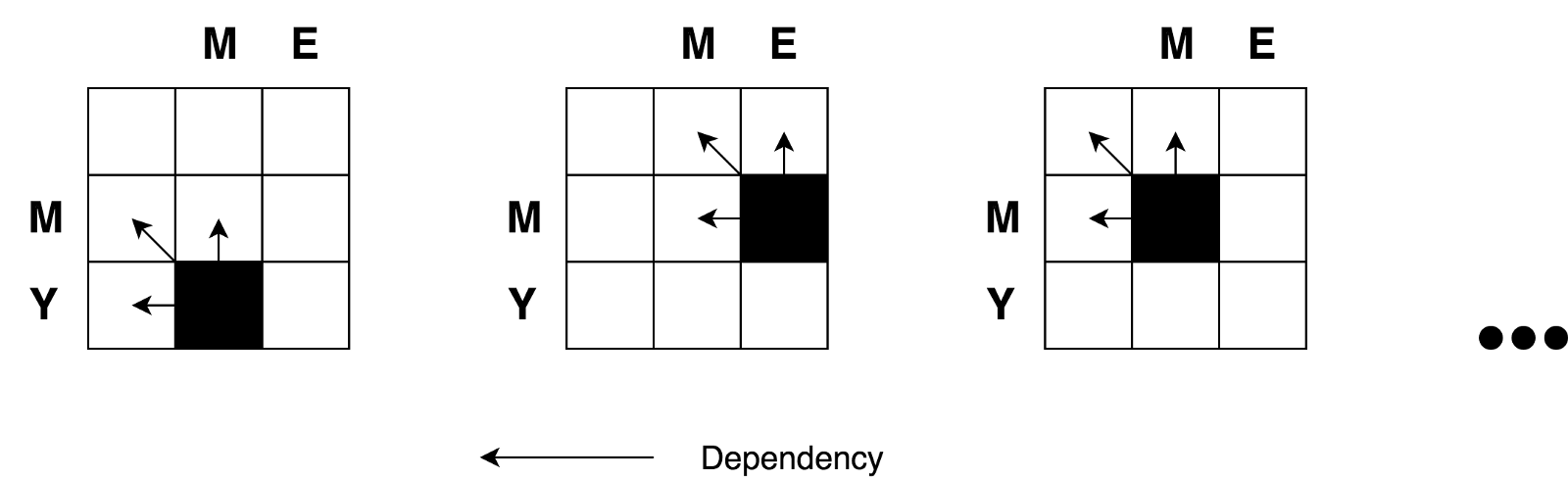
الخبر السار هو أنه وفقًا للصيغة ، كل ما نحتاجه لحساب قيمة أي خلية ذات إحداثيات (i,j) هو فقط قيم 3 خلايا مجاورة (i-1,j) ، (i-1,j-1) و (i,j-1) . كل ما نحتاجه هو العثور على القيمة الدنيا لثلاث خلايا مجاورة وإضافة خلية واحدة (+1) إلى هذه القيمة إذا كان لدينا أحرف مختلفة في الصف الأول والعمود العاشر.

مرة أخرى ، يمكنك أن ترى بوضوح الطبيعة العودية لهذه المهمة.



لقد رأينا أيضًا أننا كنا نتعامل مع مهمة فرق تسد. ولكن ، هل يمكننا تطبيق البرمجة الديناميكية لحل هذه المشكلة؟ هل تفي هذه المهمة بشروط " المشاكل المتداخلة " و " الهياكل الفرعية المثلى " المذكورة أعلاه؟ نعم دعونا نبني شجرة قرار.



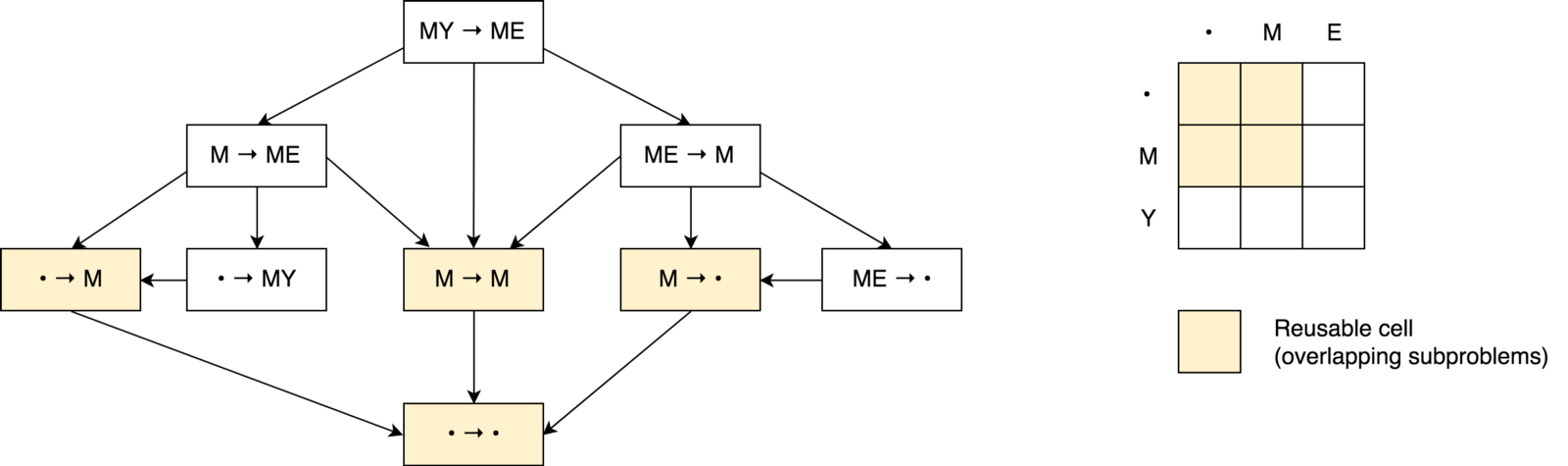
أولاً ، قد تلاحظ أن شجرة القرار لدينا تبدو أكثر مثل الرسم البياني للقرار وليس شجرة . قد تلاحظ أيضًا العديد من المهام الفرعية المتداخلة . كما يُلاحظ أنه من المستحيل تقليل عدد العمليات وجعلها أصغر من عدد العمليات من الخلايا الثلاث المجاورة (مشاكل فرعية).

قد تلاحظ أيضًا أن القيمة في كل خلية يتم حسابها بناءً على القيم السابقة. وبالتالي ، في هذه الحالة ، يتم استخدام تقنية الجدولة (ملء ذاكرة التخزين المؤقت في الاتجاه من الأسفل إلى الأعلى). سترى هذا في مثال الرمز أدناه.

بتطبيق كل هذه المبادئ ، يمكننا حل مشاكل أكثر تعقيدًا ، على سبيل المثال ، مهمة التحول السبت → الأحد:



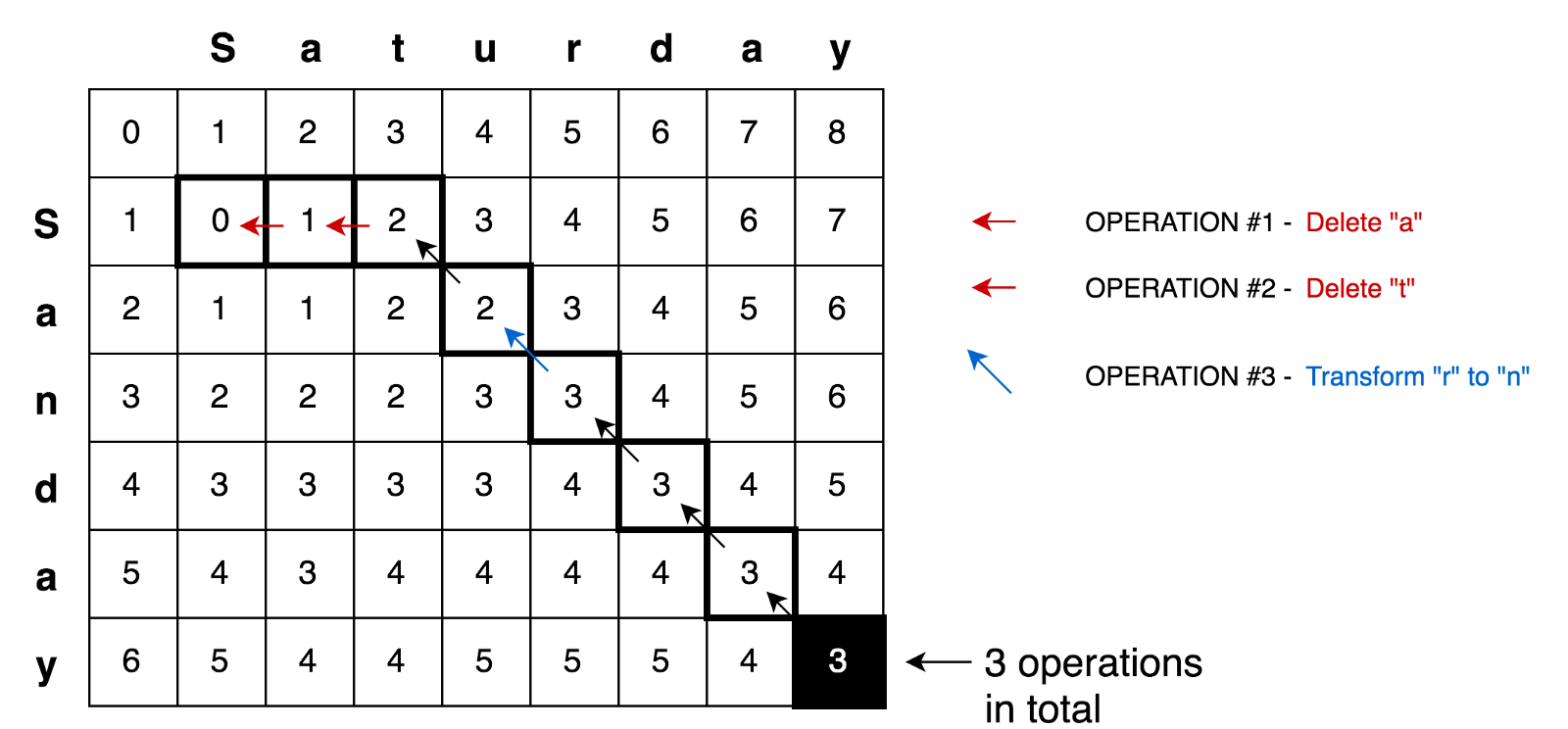مثال على الرمز

هنا يمكنك إيجاد حل كامل لإيجاد الحد الأدنى لمسافة التحرير بالاختبارات والتفسيرات:

 function levenshteinDistance(a, b) { const distanceMatrix = Array(b.length + 1) .fill(null) .map( () => Array(a.length + 1).fill(null) ); for (let i = 0; i <= a.length; i += 1) { distanceMatrix[0][i] = i; } for (let j = 0; j <= b.length; j += 1) { distanceMatrix[j][0] = j; } for (let j = 1; j <= b.length; j += 1) { for (let i = 1; i <= a.length; i += 1) { const indicator = a[i - 1] === b[j - 1] ? 0 : 1; distanceMatrix[j][i] = Math.min( distanceMatrix[j][i - 1] + 1, // deletion distanceMatrix[j - 1][i] + 1, // insertion distanceMatrix[j - 1][i - 1] + indicator, // substitution ); } } return distanceMatrix[b.length][a.length]; } 

الاستنتاجات

في هذه المقالة ، قارنا بين نهجين خوارزميين ("البرمجة الديناميكية" و "فرق تسد") لحل المشكلات. وجدنا أن البرمجة الديناميكية تستخدم مبدأ "فرق تسد" ويمكن تطبيقها على حل المشكلات إذا كانت المشكلة تحتوي على مشاكل فرعية متقاطعة والبنية التحتية المثلى (كما هو الحال مع مسافة Levenshtein). تستخدم البرمجة الديناميكية أيضًا تقنيات الاستدلال والجدولة للحفاظ على دقة فرعية لإعادة استخدامها لاحقًا.

آمل أن توضح هذه المقالة الوضع بدلاً من أن تعقد الموقف لمن حاولوا التعامل مع مفاهيم مهمة مثل البرمجة الديناميكية و "فرق تسد" :)

يمكنك العثور على المزيد من الأمثلة الخوارزمية باستخدام البرمجة الديناميكية ، مع الاختبارات والتوضيحات في مستودع JavaScript Algorithms and Data Structures .

ترميز ناجح!