"إنه سهل. نأخذ مقياس Schwarzschild ، ونبحث عن رموز Christoffel ، ونحسب مشتقاتها ، ونكتب المعادلة الجيوديسية ، ونغير بعض الإحداثيات الديكارتية (حتى لا تعاني) ، ونحصل على ODE كبير متعدد الخطوط - ونحلها. شيء من هذا القبيل ".



الآن من الواضح أن الثقوب السوداء امتصتني. إنها رائعة إلى ما لا نهاية. آخر مرة اكتشفت فيها كيفية تصور هندسة شوارزشيلد. لقد ابتلعتني مشكلة التمثيل الدقيق لكيفية تأثير انحناء مثل هذا الزمكان على مظهر السماء (حيث تتحرك الفوتونات من مصادر بعيدة على طول الخطوط الجيوديسية المنحنية بثقب أسود) لإنشاء محاكاة تفاعلية. ها هي النتيجة (يعمل في المتصفح). الحيلة هي تعظيم حساب انحراف الأشعة الضوئية. كل شيء يعمل بشكل أو بآخر بشكل طبيعي ، ولكن بالطبع ، هذه المحاكاة بعيدة كل البعد عن المثالية ، لأنه في الواقع لا يوجد تتبع هناك (لغير المتخصصين: استعادة موقع أشعة الضوء التي تقع في الكاميرا في الوقت المناسب).

يصحح مشروعي الجديد هذا النقص عن طريق التخلي عن الكفاءة / التفاعل بأبسط طريقة ممكنة: هذا هو أداة تتبع الأشعة فقط على وحدة المعالجة المركزية . يتم إجراء التتبع بدقة وأطول فترة ممكنة. استغرق تقديم الصورة أعلاه 15 دقيقة (شكرا ، RK4) على جهاز الكمبيوتر المحمول الخاص بي.

لا يوجد تحسن مقارنة بالأعمال المماثلة. أنا أستمتع حقًا بفعلها. أكتب هذه المقالة لمشاركة النتائج ليس فقط ، مثل الصورة أعلاه ( خاصة وأن البعض الآخر كان أفضل ) ، ولكن أيضًا عملية إنشاء هذه الصور ، مع مناقشة / شرح الفيزياء والتنفيذ. من الناحية المثالية ، يمكن أن يلهم هذا أو يصبح دليلاً للأشخاص ذوي الاهتمامات المماثلة.

ابحث عن تصميمات جديدة للعلامة بدون نجوم على tumlr.

قليلا من البصريات الزائفة ريمان

الظل

إذا كنت قد جربت بريمجتي بالفعل ، فأنت على دراية بهذه الصورة:



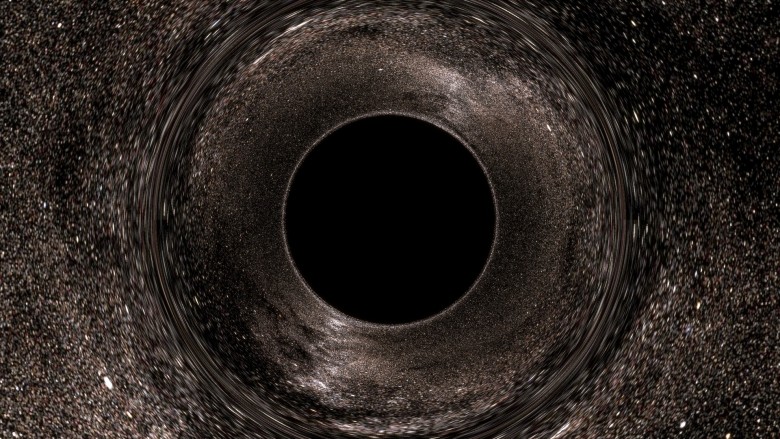
يسلط الضوء على الميزات الرئيسية: قرص أسود وحلقة تشويه غريبة.

غالباً ما تنتبه المناقشات: من الخطأ أن نقول أن القرص الأسود هو أفق الحدث. في الواقع ، من الخطأ القول بأن منطقة الصورة هي كائن . هذه صورة لكائن. في الواقع ، هناك مسارات ، عند التتبع من عينك إلى المصدر ، ستظهر في أفق الحدث (GS). هذه هي وحدات البكسل السوداء ، حيث لا يمكن لأي فوتون أن يتبع هذا المسار من ثقب أسود (BH) إلى عينك. وبالتالي ، فإن هذا القرص الأسود هو صورة واضحة لأفق الحدث ، بمعنى أنه إذا قمت برسم شيء (في الماضي البعيد) فوق الأفق مباشرة ، فسيتمكن المراقبون الخارجيون من رؤيته مباشرة على هذا القرص الأسود (سنقوم بالفعل بتنفيذ هذا التجربة لاحقًا). في بعض المنشورات ، تسمى هذه المنطقة السوداء أيضًا "ظل" BH.



ومع ذلك ، من المثير للاهتمام ملاحظة أن هذه أيضًا صورة لكرة الفوتون (PS). يصور الرسم البياني gnuplot في الأعلى الجيوديسيا للفوتونات الواردة من اللانهاية (النظر إلى BH من مسافة عند التكبير) مع GS (أسود) و FS (أخضر). نصف قطر المجال الفوتوني أكبر 1.5 مرة من نصف قطر أفق الحدث (في هندسة شوارزشيلد) وهنا يسمح بالمدارات الدائرية للفوتونات حول الثقب الأسود (وإن كان غير مستقر). على الرسم البياني ، تقع بعض الأشعة في عدم الوجود ، في حين أن البعض الآخر مبعثر (وبالتالي يظهر في نقطة أخرى في المجال السماوي). يمكن ملاحظة أنه بالنسبة للأشعة الممتصة ، تكون معلمة التعريض أقل من ~ 2.5 نصف قطر. هذا هو نصف القطر الظاهر للقرص الأسود ، وهو أكبر بكثير من GS و FS.

على أي حال ، فإن الحقيقة التالية مهمة:

سيصل حادث شعاع ضوئي بحرية في مجال الفوتون أيضًا إلى أفق الحدث.

هذا يعني أن صورة المجال الفوتوني مدرجة في صورة أفق الحدث. ولكن بما أن GS تقع بوضوح داخل FS ، يجب أن تكون صورة الأولى أيضًا مجموعة فرعية من الأخيرة. ثم يجب أن تتطابق الصورتان.

لماذا نتحقق من أن القرص الأسود هو أيضًا صورة لـ FS؟ لأن هذا يعني أن حافة القرص الأسود مليئة بالفوتونات التي تنزلق على طول كرة الفوتون. تتوافق البكسل الموجود خارج القرص الأسود مباشرة مع الفوتون ، والذي (عند تتبعه) يسقط حلزونيًا في كرة الفوتون ، أقرب وأقرب إلى مدار دائري غير مستقر ، يدور عدة مرات (كلما نظرت أقرب ، كلما أسرع في الدوران) ، ثم ينبثق في دوامة - لأن المدار غير مستقر - ويهرب إلى ما لا نهاية.

سيؤدي هذا السلوك إلى تأثير بصري مثير للاهتمام مشابه للفاصل في نظام ديناميكي. من الناحية النظرية ، إذا تم إطلاق الحزمة تمامًا على طول الحافة ، فسوف تدور إلى الأبد في دوامة ، أقرب وأقرب إلى المدار الدائري لكوكب الفوتون.

التأثير على المجال السماوي

لن نركز على هذا الموضوع ، لأن البرنامج الصغير مخصص له ، ويعطي فكرة أفضل بكثير عن التشوهات في السماء (بما في ذلك خيار شبكة الأشعة فوق البنفسجية لمزيد من التشوهات الواضحة).

بضع كلمات حول خاتم أينشتاين. يمكن تمييز عدسة الجاذبية بصريًا لأنها صورة لنقطة مفردة ، تقع مباشرة مقابل المراقب. يتم تشكيل الحلقة عند زاوية العرض هذه عندما تنحني الأشعة من الراصد بالتوازي. الأشعة الخارجية ليست منحنية بما يكفي وتبقى متباينة ؛ في الداخل ينحني كثيرًا ، وفي الواقع يمكن أن يتراجع إلى الوراء أو في دائرة ، كما رأينا.

لكن فكر في هذا: إذا اقتربت بما يكفي من القرص الأسود ، يمكن أن تشكل أشعة الضوء دائرة واحدة ، ثم تتوازي. هناك يجب أن نرى حلقة أينشتاين الثانوية. في الواقع ، يمكن أن يكون هناك حلقات من أي ترتيب (أي عدد من اللفات). يجب أن يكون هناك أيضًا حلقات "غريبة" بينها ، حيث تنحني أشعة الضوء بشكل متوازٍ ، ولكنها موجهة نحو المشاهد. توجد هذه السلسلة اللامتناهية من الحلقات ، لكنها غير مرئية تمامًا في صورتنا (في الواقع ، في معظم هذه الصور) ، لأنها قريبة جدًا من حافة القرص.

تشويه أفق الحدث

شيء ما تغير في هذه الصورة الجديدة. بادئ ذي بدء ، فهي مصنوعة بدقة أفضل وبتصفية خلفية لجعلها أكثر تميزًا. ثم قمت بتكبير صورة BH (لا تقترب ، ما زلنا على مسافة 10 أقطار نصف قطر عنها ، مجرد تكبير). لكن الأهم من ذلك أنني رسمت شبكة في الأفق .

الأفق "مجرد كرة". من الناحية الفنية ، فهي ليست كرة ريمانية قياسية بمقياس مكاني. الأفق يشبه الضوء! هذه طريقة ملونة للقول إنها تنتقل بسرعة الضوء. ومع ذلك ، في إحداثيات شوارزشيلد ، لا يزال السطح $$$r = 1$ ويمكننا استخدامها $$$\ phi$ و $$$\ theta$ مثل خط الطول وخط العرض. وبالتالي ، يمكن رسم الشبكة بطريقة قانونية. تراها في الصورة.

تتيح لك الشبكة رؤية تأثير خاص يمكن اشتقاقه إذا قمنا بتحليل منحنى التشتت / الامتصاص للفوتونات أعلاه:

يمكن رؤية سطح الأفق بالكامل في وقت واحد من أي نقطة.

هذا مثير جدا للاهتمام. عندما تنظر إلى كرة ثابتة في زمان قياسي ثابت ، لا ترى أكثر من 50٪ من سطحها في أي لحظة من الوقت (إذا اقتربت ، فهي أقل من 50٪ بسبب المنظور). لكن الأفق مرئي في نفس الوقت الذي يظهر فيه قرص أسود: انتبه ، على وجه الخصوص ، إلى القطبين الشمالي والجنوبي. ومع ذلك ، على الرغم من وضع السطح بالكامل على قرص أسود ، إلا أنه لا يغطيه بالكامل : إذا قمت بتكبير الصورة على الحافة ، سترى أن صورة GE تنتهي إلى نهاية الظل. ستجد حلقة تقع قريبة جدًا من الحافة الخارجية ، ولكن ليس حتى النهاية. هذه الصورة هي نقطة مقابل المراقب وتحدد حدود هذه الصورة "الأولى" لـ HS في الداخل. فما هو بين هذا الخاتم والحافة الفعلية؟ لم أقم بعد بإنشاء صورة مكبرة ، ولكن هناك صورة كاملة أخرى لأفق الحدث . ثم واحدة أخرى ، إلى أخرى إلى ما لا نهاية. هناك صور متحدة المركز للأفق بأكمله ، مضغوطة في الظل. (شكرا جزيلا / u / xXxDeAThANgEL99xXx للإشارة إلى هذه الظاهرة التي فاتني) .

إضافة قرص تنامي

ماذا سيفعل العرض الحديث لـ BH بدون قرص تراكم؟ على الرغم من أن هذا سؤال قابل للنقاش بشكل واضح ، إلا أن Nolan's Interstellar متاح حقًا للمراقبة ، ناهيك عن الدقة ، ولكن يجب علينا بالتأكيد أن نشكر الفيلم الرائج لنشره تشويهًا معينًا لقرص التنامي. هنا لدينا قرص تراكم أفقي رفيع للغاية ومسطح يمتد من كرة الفوتون (على الرغم من أن هذا غير واقعي للغاية لأن المدارات أقل $$$3r_S$ غير مستقر ، كما هو موضح أدناه) ما يصل إلى 4 أقطار ، مطلية في قفص أبيض وأزرق. مع هذا اللون ، من الواضح أننا نواجه حالة أخرى ، عندما يكون 100 ٪ من سطح الجسم مرئيًا في نفس الوقت.

لهذه الصورة ، حركت المراقب أعلى قليلاً للنظر إلى القرص قليلاً من الأعلى. تشاهد صور وجهين للقرص : الجزء العلوي والسفلي. تنحني الصورة في قوس فوق ظل الثقب الأسود لأن الشعاع الموجّه مباشرة فوق الثقب الأسود ينحني لأسفل ليلتقي السطح العلوي للقرص خلف الثقب ، مقابل المراقب.

وهذا يفسر أيضًا وجود الصورة السفلية: فالأشعة تحت BH تنحني إلى السطح السفلي للقرص ، خلف BH. إذا نظرت عن كثب ، تنتشر الصورة في جميع أنحاء الظل ، ولكن في الجزء العلوي تكون أرق كثيرًا. هذا يتوافق مع أشعة الضوء التي تقع فوق BH ، وجعل دائرة كاملة تقريبًا حول الحفرة وضرب السطح السفلي أمام القرص.

بالطبع ، من السهل استنتاج أن هناك عددًا لا نهائيًا من صور أقراص التنامي التي تنحسر بسرعة كبيرة عند اقترابها من الحافة. الصورة التالية رقيقة جدًا بالفعل ، بالكاد يمكن رؤيتها في الجزء السفلي من الحافة.

صور GIF لا تزال ذات صلة

في هذه الرسوم المتحركة المتشنجة ، أقوم بتشغيل / إيقاف انحراف الضوء (رسميًا Schwarzschild / Minkowski) لتوضيح بعض النقاط التي تحدثنا عنها.





يتم إنشاء هذين الصور المتحركة الغريبة بناءً على طلب القراء. في البداية ، يدور المراقب حول ثقب أسود على مسافة 10 أقطار. لا ينبغي فهم هذا على أنه مدار فعلي ، لأنه في الواقع لا يوجد انحراف عند الانتقال إلى المدار. هنا سلسلة من صور BH الثابتة من عدة نقاط حيث يتحرك المراقب من مكان إلى آخر بين الإطارات ؛ إنه مدار "ثابت الحرارة" ، إذا أردت.

ولا يزال الاستريو ذا صلة

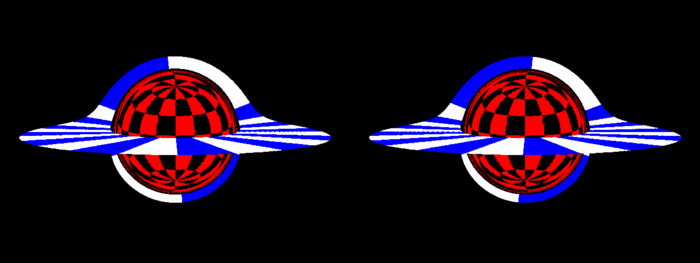
من المثير للاهتمام ، أن الظل يبدو مسطحًا جدًا.

كفى العلم

لدينا صور غنية بالمعلومات بأسلوب التسعينيات بدقة منخفضة بألوان سامة. فيما يلي بعض الاداءات "البوب" (انقر للحصول على الحجم الكامل).


تم إنشاء هذه الصورة بواسطة user / n / dfzxh مع المسح بأربعة أضعاف


خطة أكبر


صورة مكبرة للخاتم


تأثير عبادة "حلقة الضوء" عند النظر إليها من المستوى الاستوائي


إذا قمت بتنزيل البرنامج ، فهذا هو المشهد الحالي بشكل افتراضي


حملة أوسع بكثير

حسنًا ، نعم ، لا شيء مميز. لا يوجد عمل فني ، مجرد الاداءات من البرنامج. دعنا نعود مؤقتًا إلى العلم: الصورة الثالثة ، التي يبدو أنها لا معنى لها ، هي في الواقع ذات قيمة كبيرة. هذه هي المساحة المتضخمة بين الحافة العلوية للقرص الأسود والصورة الرئيسية لقرص التنامي. الراصد موجود على الحافة الخارجية لقرص التنامي نفسه ويكبر الصورة. كان الهدف هو تصوير أكبر عدد ممكن من الحلقات من مختلف الأوامر. تظهر ثلاثة أوامر: المنطقة الأفتح في الجزء العلوي ليست سوى الحافة السفلية للصورة الأولى للسطح البعيد العلوي للقرص. الشريط أدناه ، تحت البحر الهادئ للنجوم الممتدة ، هو الجزء العلوي من صورة الجزء الأمامي السفلي من القرص. في الجزء السفلي - خط رفيع من الضوء بعرض لا يزيد عن بكسل ، ملتصق بالقرص الأسود في كرة الفوتون. هذه هي الصورة الثالثة في الأساس: مرة أخرى ، السطح العلوي البعيد ، ولكن بعد أن أكمل الضوء ثورة إضافية حول الثقب الأسود. اندمجت معها ، ولكن الصور الأكثر نحافة بشكل متزايد هي حلقات ذات ترتيب أعلى. حسنًا ، هذا أيضًا يستحق علامة <blockquote>:

هناك صور لا حصر لها لكل من الأسطح العلوية والسفلية لقرص التنامي ، وتظهر جميعها سطح القرص بالكامل في نفس الوقت. علاوة على ذلك ، باستثناء الصورة الأولى ، لا تمر هذه الصور أمام القرص الأسود ولا أمام بعضها البعض ، وبالتالي فهي "متحدة المركز".

رائع.

أنا أقبل طلبات التقديم
هل أنت مهتم بتصور محدد ، ولكنك لست مستعدًا للتغلب على صعوبات تثبيت البرنامج وتقديم نفسك؟ فقط أرسل لي رديت أو أرسل لي . لا يستغرق تقديم 1080 بكسل على الكمبيوتر المحمول أكثر من 10-20 دقيقة.

قرص تنامي واقعي

قرص التنامي في الاداءات كارتوني جميل. إنه مجرد قرص نسيج غبي. ماذا يحدث عندما يتم تضمين الفيزياء الحقيقية في المظهر المرئي للقرص؟ ماذا يحدث عندما تفكر في الانزياح الأحمر من الحركة المدارية ، على سبيل المثال؟

من النماذج الشائعة لقرص التنامي قرصًا رفيعًا للغاية من المادة في مدار دائري تقريبًا. يبدأ بـ ISCO (المدار الدائري المستقر الداخلي ، $$$3r_s$ ) مع ملف تعريف درجة الحرارة وفقًا لقانون الطاقة $$$(T \ sim r ^ {- a}$ . سأستخدم خيارًا بسيطًا جدًا:

$$

$$T \ sim r ^ {- 3/4}$$

وهو أمر غير طبيعي بالتأكيد في النظرية النسبية العامة للسوائل الواقعية ، ولكن هنا (على أي حال ، لن تلاحظ الفرق).

الآن المعلمة المجانية هي مقياس شائع لدرجات الحرارة ، على سبيل المثال ، درجة الحرارة في ISCO. هذه درجة الحرارة ضخمة لمعظم الثقوب السوداء. نحن نتحدث عن مئات الملايين من كلفن. من الصعب تخيل أي قطعة أثرية بشرية يمكن أن توجد تحت تأثير إشعاع القرص (الذروة في إشعاع الأشعة السينية) في درجات الحرارة هذه ، ناهيك عن التصوير الفوتوغرافي. لذا من الواضح أننا بحاجة إلى خفض درجة الحرارة. من الواضح أن الثقوب السوداء الهائلة أكثر برودة ، لكنها ليست كافية. نحن بحاجة إلى الهبوط إلى 10000 K في ISCO حتى نتمكن من رؤية شيء على الأقل. هذا غير دقيق للغاية ، ولكن هذا كل ما يمكنني فعله.

يجب طرح سؤالين. أولاً: ما لون الجسم الأسود عند درجة الحرارة هذه؟ ثانيًا: ما مدى سطوعها ؟ من الناحية الرسمية ، فإن الإجابة على هذين السؤالين هي في المنتج التدريجي للوظائف التي تصف القنوات R و G و B مع طيف الجسم الأسود. في الممارسة العملية ، يتم استخدام بعض التقديرات.

بالنسبة لصيغة تانر هيلاند ، فهي دقيقة وفعالة للون ، ولكنها تتضمن العديد من الشروط غير الممكنة مع تتبع الأشعة الخاص بي (انظر أدناه لمزيد من التفاصيل). أسرع طريقة هي استخدام نسيج بسيط:



هذا الملمس هو واحد من العديد من الأشياء المفيدة في اختيار Mitchell Charity لـ "ما هو لون الجسم الأسود؟" . كمرجع ، يتوافق مع النقطة البيضاء E (النقطة البيضاء E).

يوضح المقياس لون الجسم الأسود عند درجات حرارة من 1000 كلفن إلى 30 ألف كلفن ، مع درجات حرارة أعلى تقابل نفس درجة اللون الأزرق تقريبًا. نظرًا لوجود فرق كبير في السطوع بين درجات الحرارة ، لا يمكن لهذا النسيج أن ينقل السطوع ولا ينقله ؛ بدلا من ذلك ، تطبيع الألوان. مهمتنا هي حساب السطوع النسبي وتطبيقه. صيغة تحليلية مناسبة لذلك. إذا افترضنا أن الطيف المرئي ضيق للغاية ، فإن الشدة المرئية الإجمالية تتناسب مع طيف الجسم الأسود نفسه:

$$

$$\ frac {1} {\ lambda ^ 5} \ frac {1} {\ exp (\ frac {hc} {\ lambda k_B T}) - 1}$$

حيث تخلصت من الثوابت الشائعة الغبية (ما زلنا بصدد توسيع السطوع لرؤية شيء ما). يمكنك ببساطة إدراج $$$\ lambda$ تقريبًا للنطاق المرئي من الطيف ، ونحصل على أن السطوع يتناسب مع درجة الحرارة وفقًا لهذه الصيغة:

$$

$$(e ^ {\ frac {29622.4 \ text {K}} {T}} - 1) ^ {- 1}$$

إنه بسيط للغاية. على سبيل الاختيار ، نلاحظ أن الكثافة النسبية تنخفض بسرعة إلى الصفر مع اقتراب T من الصفر ، ولا تتغير عمليًا عندما تنتقل T إلى ما لا نهاية.

الانزياح الأحمر

ناقشنا السرعات المدارية في هندسة Schwarzschild في وصف التطبيق الصغير. لحساب الانزياح الأحمر ، يتم استخدام صيغة الانزياح الأحمر من SRT:

$$

$$(1 + z) _ \ text {Doppler} = \ frac {1 - \ beta \ cos (\ theta)} {\ sqrt {1- \ beta ^ 2}}$$

حيث $$$\ cos (\ theta)$ - جيب التمام للزاوية بين اتجاه الحزمة المنبعثة من القرص والسرعة المحلية للقرص ، محسوبة في نظام الإحداثيات بالقصور الذاتي المحلي لشوارزشيلد. الصيغة صحيحة في هذا السياق بسبب مبدأ التكافؤ.

يجب ضربه في معامل الانزياح الأحمر الثقالي:

$$

$$(1 + z) _ \ text {Gravitational} = (1 - r ^ {- 1}) ^ {- 1/2}$$

لا يعتمد هذا المعامل على مسار شعاع الضوء ، ولكن فقط على نصف قطر الإشعاع ، لأن هندسة Schwarzschild ثابتة.

وهذا يعني أيضًا أن مساهمة موقع المراقب في الانزياح الأحمر الثقالي تكون ثابتة على كامل مجال الرؤية. تحتوي صورتنا بأكملها على تحول أزرق عام ثابت ، لأننا عميقون في BH. لذلك ، يعطي هذا التأثير ظلًا خافتًا فقط يمكن تجاهله.

نحن أيضًا نتجاهل الانزياح الأحمر من حركة المراقب ، لأن مراقبنا ثابت في هندسة Schwarzschild. ها هي النتيجة النهائية:



كما ترى ، فإن معظم القرص أبيض بالكامل بسبب أقصى سطوع في قنوات الألوان. إذا قمت بخفض هذه القنوات إلى نطاق 0.0-1.0 ، فستصبح الأجزاء الخارجية من القرص شاحبة أو سوداء.زيادة السطوع كبيرة جدًا بحيث لا يمكن رؤيتها وتقديرها. لقد حاولت إظهار التأثير باستخدام المعالجة اللاحقة حتى تظهر الأجزاء الأكثر سطوعًا انتقالًا للون ، ولكن هذا لا يكاد يكفي.

صورة مربكة جدا. هذه صورة بدون مراعاة السطوع ، حيث يمكنك تقييم الألوان:



هذه الصور ذات دقة أقل ، لأنها تستغرق وقتًا طويلاً جدًا لعرضها على جهاز الكمبيوتر المحمول الخاص بي (الجذور التربيعية سيئة ، الأطفال).

على أي حال ، فإن هذا العرض أقل إثارة بألف مرة من الآخرين (بشكل رئيسي لأن الحافة الداخلية للقرص بعيدة بالفعل بما يكفي عن GS ، وبالتالي فإن العدسة كبيرة جدًا) ، ولكن العرض على الأقل دقيق . إذا وجدت ثقبًا أسود بدرجة حرارة 10000 كلفن ونظارات شمسية جيدة ، فسترى ذلك بالضبط.

لقطة أخرى عن قرب. لقد رفعت تشبع الجمال بشكل غير طبيعي:

كتابة جهاز تتبع شعاع الثقب الأسود

مصدر جيثب

هناك فرق كبير وواضح للغاية بين بصريات الثقوب السوداء والمدمج الرقمي ، الذي ينتج خلفيات سطح مكتب جميلة بدقة 1080 بكسل. في المرة الأخيرة لم أنشر تعليلي ، لكنني ببساطة أثيرت مستودعًا كبيرًا وقذرًا. الآن أريد أن أشرح بالتفصيل أكثر قليلاً ، وأحاول أيضًا الحفاظ على الشفرة بشكل أكثر دقة وبتعليقات.

لم يتم إنشاء التتبع الخاص بي جيدًا وقويًا وسريعًا. بادئ ذي بدء ، كنت أرغب في أن يكون من السهل إعدادها ، لجعلها بسيطة ، حتى يتمكن الناس من الحصول على الإلهام ورؤية إمكانية التحسين: حتى عيبها يمكن أن يشجع شخصًا ما على أن يقرر كتابة نسخته الخاصة. هنا لمحة موجزة عن الخوارزميات وتنفيذها.

إمكانات "السحر"

لذا ، النظرية العامة للنسبية ، كل شيء واضح. إنه سهل. نأخذ مقياس Schwarzschild ، ونبحث عن رموز Christoffel ، ونحسب مشتقاتها ، ونكتب المعادلة الجيوديسية ، ونغير بعض الإحداثيات الديكارتية لتجنب المعاناة اللانهائية ، ونحصل على ODE ضخم متعدد الخطوط ، ونحلها. شيء من هذا القبيل.

أنا أمزح فقط. بالطبع ، هناك خدعة واحدة.

إذا كنت تتذكر ، في المرة الأخيرة التي استنتجت فيها المعادلة التالية لمدار جسيم بلا كتلة في مستواه المداري في هندسة Schwarzschild ($$ش = 1 / ص ):$u=1/r$

$$

$$u''(\phi) + u = \frac{3}{2} u^3$$

الحيلة هي رؤية صيغة Binet هنا . لكتلة من الجسيمات النيوتونية في الإمكانات النيوتونية لمجال القوى المركزية:

$$

$$\frac{d^2}{dt^2} \vec x = \frac{1}{m} F(r)$$

ثم يتحرك الجسيم بوضوح في مستواه المداري ويتوافق مع صيغة Binet $$$u(\phi)$ :

$$

$$u'' + u = - \frac{1}{m h^2 u^2} F(u)$$

أين $$دد حزب المحافظين - عدد الوزراء،$\frac{d}{d\phi}$$$م هي الكتلة ، و$m$$$h هو الزخم الزاوي لكل وحدة كتلة. هذه معادلة للمدار ، وليست معادلة للحركة. لا تقول شيئا عن$h$$$$u(t)$ أو $$p h i ( t ) ، يظهر فقط العلاقة بين$phi(t)$$$$u$ و $$$\phi$ .

دعونا نتوقف للحظة للتفكير فيما حصلنا عليه بالفعل. تقول المعادلة أنه إذا تخيلت نظامًا ميكانيكيًا افتراضيًا للجسيم تحت تأثير قوة مركزية معينة ، فإن مساره سيكون حلًا لصيغة بينيه. ثم يصبح النظام الميكانيكي آلة حاسبة للصيغة.

هذا ما أعرضه هنا. لقد أشرنا$$$m=1$ (, ) :

$$

$$\vec F(r) = - \frac{3}{2} h^2 \frac{\hat r}{r^5}$$

أين $$$h$ — , . $$$\vec x (T)$ , $$$T$ - الإحداثيات الزمنية المجردة لهذا النظام هي في الواقع تحديد معلمات الحل الوحيد لمعادلة بينيت المقابلة ، وهي المعادلة الجيوديسية بالضبط .

لذلك ، نحل المعادلة النيوتونية في الإحداثيات الديكارتية ، والتي تعد أبسط طريقة (قررت استخدام طريقة Runge-Kutta بحيث يكون من الممكن زيادة حجم الخطوة وتقليل وقت العرض ، ولكن في المستقبل سيكون المستخدم قادرًا على اختيار طريقة حل مختلفة). ثم نحصل على الجيوديسيا الفعلية الشبيهة بالضوء ، أين $$$T$ هل المعلمة تسير على طوله (على عكس Schwarzschild $$$t$ ، ومن الزمن الطبيعي الذي لا وجود له).

هذا أفضل بكثير من الطريقة السابقة ، التي عملت مع الإحداثيات القطبية في مستوى المدار. هنا الحسابات فعالة للغاية.

تتبع راي في numpy

إذا نظرت إلى المصدر ، سترى نص Python النصي. رعب! لماذا كتابة تتبع الشعاع في Python؟ يعلم الجميع مدى بطء حلقات التكرار في Python ، والتي تضع دائمًا (تقريبًا) نهاية للعمل. والحقيقة هي أننا نجري حسابات بشكل متقطع - وبالتوازي. لهذا السبب لن يتمكن هذا البرنامج من عرض الأجزاء المرسومة بالفعل على الشاشة تدريجيًا: فهو يعرض كل شيء في نفس الوقت.

بادئ ذي بدء ، نقوم بإنشاء مجموعة من الشروط الأولية. على سبيل المثال ، مصفوفة (numPixel, 3) مع ناقلات لجميع وحدات البكسل في الصورة (numPixel - عرض الصورة × ارتفاع الصورة). ثم يتم تقليل حساب كل شعاع إلى صفائف من النوع (numPixel, ...) . نظرًا لأن العمليات مع المصفوفات في numpy سريعة جدًا ، ويتم كتابة كل شيء بشكل ثابت هنا (آمل ألا أقول أي شيء غبي الآن) ، يجب حسابه بسرعة كافية. ربما ليست C ، لكنها لا تزال سريعة. في الوقت نفسه ، لدينا مرونة ووضوح بايثون.

هذه الطريقة رهيبة لتتبع الشعاع القياسي ، حيث تنتشر الأجسام ، تعكس ، تنكسر ، ومن المهم مراعاة ظروف الإضاءة. على سبيل المثال ، يعد الانعكاس الانتقائي لأجزاء من مجموعة أشعة كابوسًا حقيقيًا. يتطلب تتبع القيم المنطقية أو مؤشرات الحلقة أقنعة متعددة ، ولا يمكن كسر الحلقات. لكن هنا حالة أخرى: جميع الأشياء في مشهدنا تنبعث منها الضوء فقط: السماء ، قرص تراكم ساخن ، أفق حدث أسود قاتم وغبار ساطع. لا يتأثرون بالضوء الساقط ، كما يمر الضوء نفسه بهدوء من خلالهم ، باستثناء تقليل الشدة. هذا يقودنا إلى خوارزمية لتحديد اللون:

خلط اللون

هذا سهل: تحتاج فقط إلى مزج جميع الكائنات بيننا ومصدر الأشعة مع قيم ألفا المقابلة لها ، ووضعها فوق بعضها البعض ، حيث سيكون أبعدها في الأسفل. نقوم بتهيئة المخزن المؤقت للألوان باللون الأسود الشفاف ألفا ، ثم عندما نتقاطع مع الكائن نقوم بتحديث المخزن المؤقت عن طريق مزج اللون من الكائن تحت المخزن المؤقت للألوان. نقوم بنفس الخطوات الخاصة بالغبار (استخدم ملف تعريف الكثافة $$$r ^ {- 2}$ ) والاستمرار في التكرار حتى النهاية. لاحظ أن قناة ألفا تعمل أيضًا كمخزن مؤقت Z ، حيث يتوقف الكائن عن المساهمة بعد أن يعبر الشعاع الكائن المعتم (الذي يضبط قيمة ألفا للمخزن المؤقت على 1.0).

العيب الواضح لهذه الطريقة هو أنه لا يمكنك التوقف عن تتبع الأشعة بعد حسابها ، لأنها جزء من الصفيف حيث يستمر تتبع الأشعة الأخرى. على سبيل المثال ، بعد التصادم مع الأفق ، تستمر الأشعة بالتجول بشكل عشوائي بعد أن تسقط في التفرد - يمكنك رؤية ما يحدث إذا قمت بإيقاف تشغيل كائن الأفق بشكل صريح. تضمن خوارزمية مزج ألفا أنها لا تؤثر على الصورة النهائية ، ولكن هذه الأشعة لا تزال تحمل وحدة المعالجة المركزية.