توزيع النقاط بالتساوي عبر الكرة في pytorch و tensorflow

تم كتابة هذا النص لأولئك الذين يرغبون في التعلم العميق ، الذين يرغبون في استخدام طرق مختلفة من مكتبات pytorch و tensorflow لتقليل وظيفة العديد من المتغيرات ، الذين يرغبون في تعلم كيفية تحويل برنامج تم تنفيذه بالتسلسل إلى حسابات مصفوفة متجهية تتم باستخدام numpy. يمكنك أيضًا تعلم كيفية عمل رسم كاريكاتوري من البيانات المصورة باستخدام PovRay و vapory.

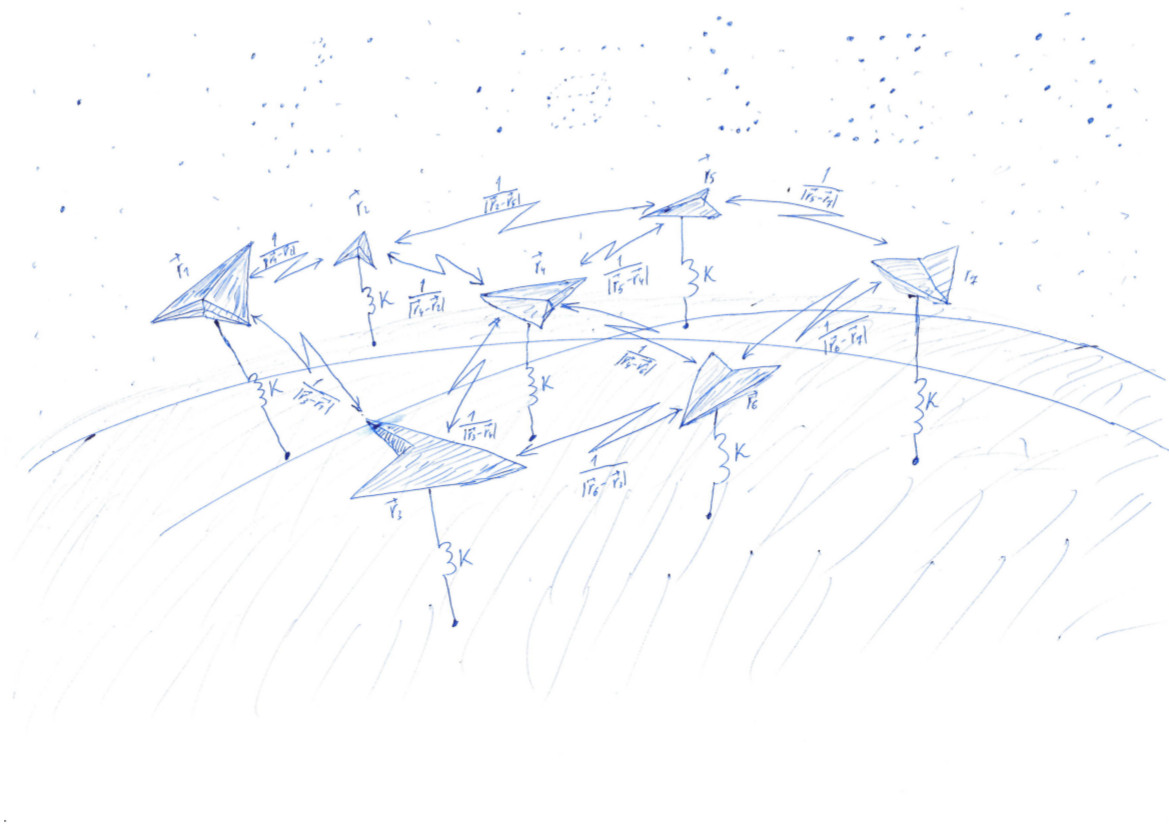
من أين المهمة

كل يقلل من وظائفه (ج) عالم البيانات المجهول

في أحد المنشورات السابقة لمدونتنا ، وبالتحديد في فقرة "Rake No. 6" ، تحدثنا عن تقنية DSSM ، والتي تتيح لك تحويل النص إلى متجهات. للعثور على مثل هذا التعيين ، يحتاج المرء إلى العثور على معاملات التحولات الخطية التي تقلل من وظيفة الخسارة المعقدة إلى حد ما. إن فهم ما يحدث عندما يكون تعلم مثل هذا النموذج صعبًا بسبب الأبعاد الكبيرة للمتجهات. لتطوير حدس يسمح لك باختيار طريقة التحسين وتعيين معلمات هذه الطريقة ، يمكنك التفكير في نسخة مبسطة من هذه المهمة. الآن دع المتجهات تكون في فضاءنا المعتاد ثلاثي الأبعاد ، ثم يسهل رسمها. وستكون وظيفة الخسارة هي إمكانية دفع النقاط بعيدًا عن بعضها وجذبها إلى وحدة الكرة. في هذه الحالة ، سيكون حل المشكلة هو التوزيع الموحد للنقاط عبر المجال. من السهل تقييم جودة الحل الحالي بالعين.

لذا ، سنبحث عن توزيع موحد على نطاق كمية معينة $$$n$ النقاط. يكون مثل هذا التوزيع ضروريًا في بعض الأحيان للصوتيات من أجل فهم اتجاه إطلاق موجة في البلورة. Signalman - لمعرفة كيفية وضع الأقمار الصناعية في المدار لتحقيق أفضل جودة اتصالات. أخصائي الأرصاد الجوية - لوضع محطات رصد الطقس.

بالنسبة للبعض $$$n$ يتم حل المهمة بسهولة . على سبيل المثال ، إذا $$$n = 8$ ، يمكننا أن نأخذ المكعب وستكون رؤوسها الجواب على المشكلة. نحن محظوظون أيضا إذا $$$n$ ستكون مساوية لعدد رؤوس القمم المجسمة أو الاثني عشرية أو الصلبة الأفلاطونية الأخرى. وإلا ، فإن المهمة ليست بهذه البساطة.

للحصول على عدد كبير بما فيه الكفاية من النقاط ، هناك صيغة مع معاملات مختارة تجريبياً ، وهناك العديد من الخيارات هنا ، هنا ، هنا ، وهنا . ولكن هناك حل أكثر شمولية ، وإن كان أكثر تعقيدًا ، تم تخصيص هذا المقال له.

نحل مشكلة مشابهة جدًا لمشكلة طومسون ( ويكي ). مبعثر $$$n$ بشكل عشوائي ، ثم اجعلها تجذب إلى سطح ، مثل كرة ، وتدفع من بعضها البعض. يتم تحديد الجذب والنفور حسب الوظيفة - المحتملة. عند الحد الأدنى لقيمة الوظيفة المحتملة ، ستقع النقاط على الكرة بالتساوي.

تشبه هذه المهمة إلى حد كبير عملية التعلم لنماذج التعلم الآلي (ML) ، والتي يتم خلالها تقليل وظيفة الخسارة. لكن عالم البيانات عادة ما يراقب كيف ينخفض ​​رقم واحد ، ويمكننا مشاهدة الصورة تتغير. إذا نجحنا ، سنرى كيف تتباعد النقاط بشكل عشوائي داخل المكعب مع الجانب 1 متباينة على طول سطح الكرة:

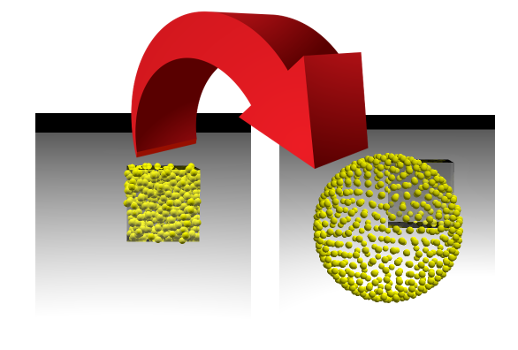
من الناحية التخطيطية ، يمكن تمثيل خوارزمية حل المشكلة على النحو التالي. تقابل كل نقطة تقع في مساحة ثلاثية الأبعاد صفًا من المصفوفة $$$X$ . يتم حساب دالة الخسارة من هذه المصفوفة. $$$L$ ، الذي يتوافق الحد الأدنى لقيمته مع توزيع موحد للنقاط عبر المجال. تم العثور على الحد الأدنى للقيمة باستخدام tensorflow و tensorflow ، والتي تسمح بحساب تدرج دالة الخسارة بواسطة المصفوفة $$$X$ واحصل على الحد الأدنى باستخدام إحدى الطرق المطبقة في المكتبة: SGD ، ADAM ، ADAGRAD ، إلخ.

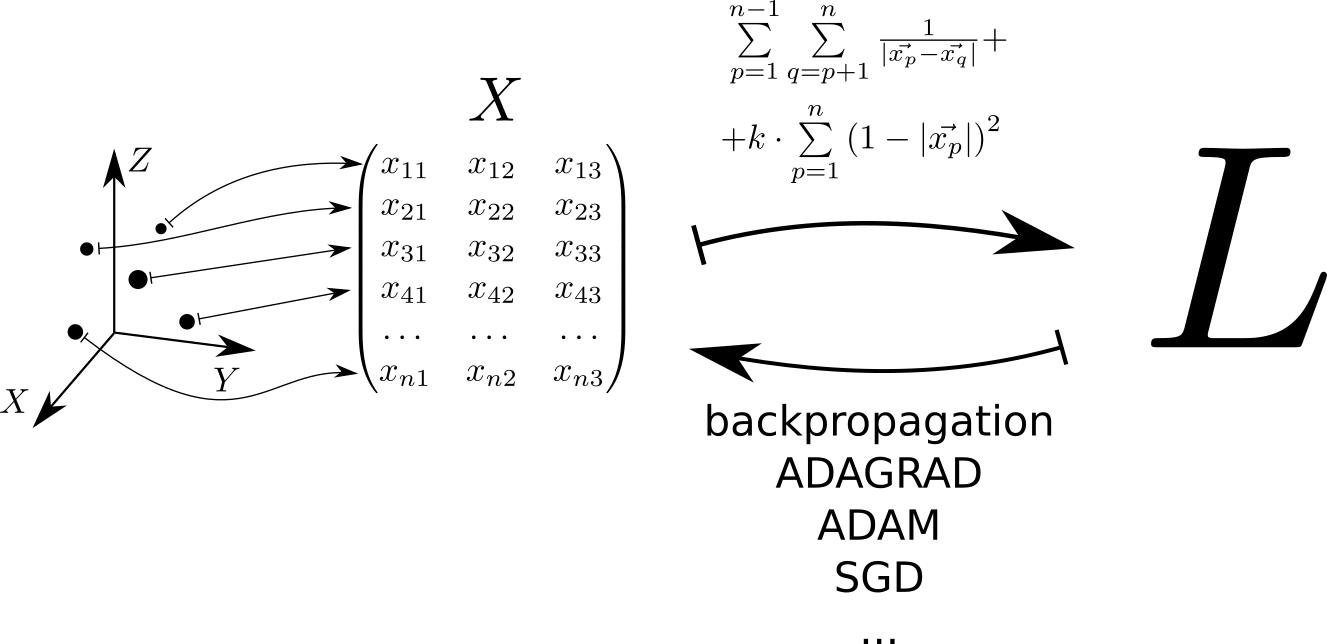
نحن نعتبر الإمكانات

نظرًا لبساطتها والتعبير عنها وقدرتها على العمل كواجهة للمكتبات المكتوبة بلغات أخرى ، يتم استخدام Python على نطاق واسع لحل مشاكل التعلم الآلي. لذلك ، تمت كتابة أمثلة التعليمات البرمجية في هذه المقالة في Python. من أجل حسابات المصفوفة السريعة ، سنستخدم مكتبة numpy. لتقليل وظيفة العديد من المتغيرات - pytorch و tensorflow.

نقوم بتفريق النقاط بشكل عشوائي في المكعب مع الجانب 1. لنحصل على 500 نقطة ، والتفاعل المرن أكثر أهمية 1000 مرة من الكهرباء الساكنة:

 import numpy as np n = 500 k = 1000 X = np.random.rand(n, 3) 

إنشاء هذا الرمز مصفوفة $$$X$ الحجم $$$3 \ مرات n$ مليئة بأرقام عشوائية من 0 إلى 1:

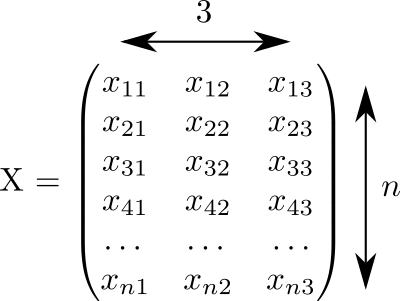
نفترض أن كل صف من هذه المصفوفة يتوافق مع نقطة واحدة. وفي ثلاثة أعمدة يتم تسجيل الإحداثيات $$$x، y، z$ كل نقاطنا.

إمكانات التفاعل المرن للنقطة مع سطح وحدة الكرة $$$u_1 = k \ cdot (1 - r) ^ 2/2$ . إمكانية التفاعل الكهروستاتيكي للنقاط $$$p$ و $$$q$ - $$$u_2 = 1 / | r_p - r_q |$ . تتكون الإمكانية الكاملة من التفاعل الكهروستاتيكي لجميع أزواج النقاط والتفاعل المرن لكل نقطة مع سطح الكرة

$$

$$U (x_1، ...، x_n) = \ sum \ limits _ {p = 1} ^ {n - 1} \ sum \ limits _ {q = p + 1} ^ {n} \ frac 1 {\ اليسار | \ vec {x_p} - \ vec {x_q} \ right | } + k \ cdot \ sum \ limits _ {p = 1} ^ n \ left (1 - | \ vec {x_p} | \ right) ^ 2 \ rightarrow \ min$$

من حيث المبدأ ، يمكن حساب القيمة المحتملة باستخدام هذه الصيغة:

 L_for = 0 L_for_inv = 0 L_for_sq = 0 for p in range(n): p_distance = 0 for i in range(3): p_distance += x[p, i]**2 p_distance = math.sqrt(p_distance) L_for_sq += k * (1 - p_distance)**2 #     ,     for q in range(p + 1, n): if q != p: pq_distance = 0 for i in range(3): pq_distance += (x[p, i] - x[q, i]) ** 2 pq_distance = math.sqrt(pq_distance) L_for_inv += 1 / pq_distance #      L_for = (L_for_inv + L_for_sq) / n print('loss =', L_for) 

ولكن هناك مشكلة صغيرة. للحصول على 2000 نقطة مثيرة للشفقة ، سيتم تشغيل هذا البرنامج لمدة 2 ثانية. سيكون أسرع بكثير إذا قمنا بحساب هذه القيمة باستخدام حسابات المصفوفة المتجهية. يتم تحقيق التسريع من خلال تنفيذ عمليات المصفوفة باستخدام اللغات "السريعة" fortran و C ، ومن خلال استخدام عمليات المعالج المتجه التي تسمح بتنفيذ إجراء على كمية كبيرة من بيانات الإدخال في دورة ساعة واحدة.

دعونا نلقي نظرة على المصفوفة $$$S = X \ cdot X ^ T$ . لديها العديد من الخصائص المثيرة للاهتمام وغالبا ما توجد في الحسابات المتعلقة بنظرية المصنفات الخطية في ML. لذا ، إذا افترضنا ذلك في صف المصفوفة $$$X$ مع المؤشرات $$$p$ و $$$q$ تتم كتابة ناقلات الفضاء ثلاثية الأبعاد $$$\ vec {r _ p} ، \ vec {r_q}$ ثم المصفوفة $$$S$ سوف تتكون من منتجات قياسية لهذه المتجهات. مثل هذه المتجهات $$$n$ القطع ، ثم البعد المصفوفة $$$S$ يساوي $$$n \ مرات n$ .

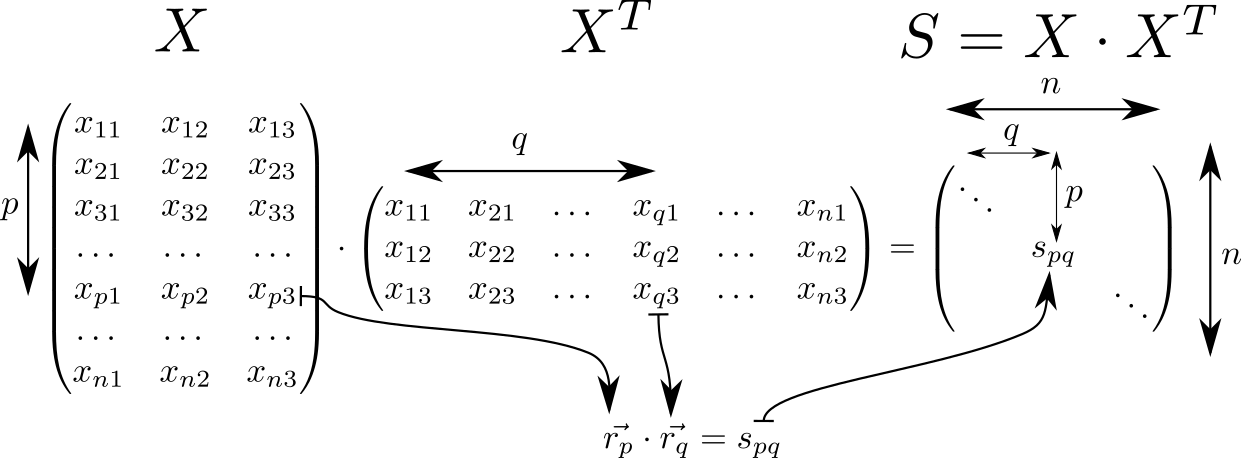
على قطر المصفوفة $$$S$ تقف مربعات أطوال ناقلات $$$\ vec {r_p}: s_ {p p} = r_p ^ 2$ . بمعرفة هذا ، دعنا نفكر في الإمكانات الكاملة للتفاعل. نبدأ بحساب مصفوفتين مساعدتين. في مصفوفة قطرية واحدة $$$S$ سيتم تكرارها في صفوف ، في أخرى - في أعمدة.

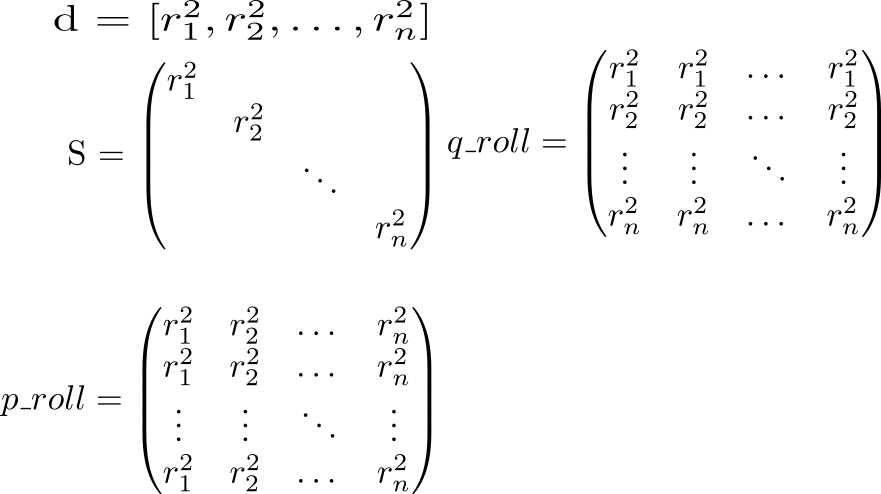
الآن دعونا نلقي نظرة على قيمة التعبير p_roll + q_roll - 2 * S

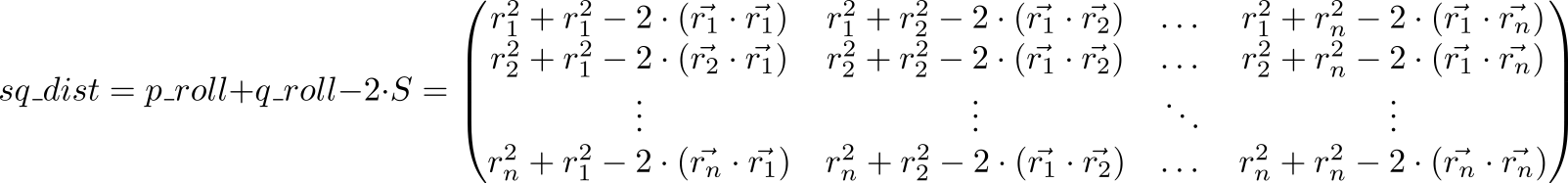
عنصر مفهرس $$$(p، q)$ مصفوفة sq_dist تساوي $$$r_p ^ 2 + r_q ^ 2 - 2 \ cdot (\ vec {r_p}، \ vec {r_q}) = (\ vec {r_p} - \ vec {r_q}) ^ 2$ . أي أن لدينا مصفوفة من مربعات المسافات بين النقاط.

النفور الإلكتروستاتيكي على الكرة

dist = np.sqrt(sq_dist) - مصفوفة المسافات بين النقاط. نحن بحاجة إلى حساب الإمكانات ، مع الأخذ في الاعتبار تنافر النقاط فيما بينها وجاذبية المجال. ضع الوحدات على القطر واستبدل كل عنصر rec_dist_one = 1 / (dist + np.eye(n)) لا تعتقد أننا rec_dist_one = 1 / (dist + np.eye(n)) المصفوفة!): rec_dist_one = 1 / (dist + np.eye(n)) . والنتيجة هي مصفوفة على القطر الذي توجد فيه وحدات ، والعناصر الأخرى هي إمكانات التفاعل الكهروستاتيكي بين النقاط.

الآن نضيف إمكانات التربيع التربيعية إلى سطح وحدة الكرة. المسافة من سطح الكرة $$$(1 - r)$ . قم بتربيعها وضربها في $$$k$ والذي يحدد العلاقة بين دور التنافر الكهروستاتيكي للجسيمات وانجذاب الكرة. المجموع k = 1000 ، all_interactions = rec_dist_one - torch.eye(n) + (d.sqrt() - torch.ones(n))**2 . دالة الخسارة التي طال انتظارها ، والتي t = all_interactions.sum() منها: t = all_interactions.sum()

برنامج يحسب الإمكانات باستخدام مكتبة numpy:

 S = X.dot(XT) #    pp_sq_dist = np.diag(S) #  p_roll = pp_sq_dist.reshape(1, -1).repeat(n, axis=0) #     q_roll = pp_sq_dist.reshape(-1, 1).repeat(n, axis=1) #     pq_sq_dist = p_roll + q_roll - 2 * S #      pq_dist = np.sqrt(pq_sq_dist) #    pp_dist = np.sqrt(pp_sq_dist) #      surface_dist_sq = (pp_dist - np.ones(n)) ** 2 #       rec_pq_dist = 1 / (pq_dist + np.eye(n)) - np.eye(n) #      L_np_rec = rec_pq_dist.sum() / 2 #     L_np_surf = k * surface_dist_sq.sum() #       L_np = (L_np_rec + L_np_surf) / n #   ,     print('loss =', L_np) 

الأمور هنا أفضل قليلاً - 200 مللي ثانية عند 2000 نقطة.

نستخدم pytorch:

 import torch pt_x = torch.from_numpy(X) # pt_x -   tensor   pytorch pt_S = pt_x.mm(pt_x.transpose(0, 1)) # mm - matrix multiplication pt_pp_sq_dist = pt_S.diag() pt_p_roll = pt_pp_sq_dist.repeat(n, 1) pt_q_roll = pt_pp_sq_dist.reshape(-1, 1).repeat(1, n) pt_pq_sq_dist = pt_p_roll + pt_q_roll - 2 * pt_S pt_pq_dist = pt_pq_sq_dist.sqrt() pt_pp_dist = pt_pp_sq_dist.sqrt() pt_surface_dist_sq = (pt_pp_dist - torch.ones(n, dtype=torch.float64)) ** 2 pt_rec_pq_dist = 1/ (pt_pq_dist + torch.eye(n, dtype=torch.float64)) - torch.eye(n, dtype=torch.float64) L_pt = (pt_rec_pq_dist.sum() / 2 + k * pt_surface_dist_sq.sum()) / n print('loss =', float(L_pt)) 

وأخيرًا tensorflow:

 import tensorflow as tf tf_x = tf.placeholder(name='x', dtype=tf.float64) tf_S = tf.matmul(tf_x, tf.transpose(tf_x)) tf_pp_sq_dist = tf.diag_part(tf_S) tf_p_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (1, -1)), (n, 1)) tf_q_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (-1, 1)), (1, n)) tf_pq_sq_dist = tf_p_roll + tf_q_roll - 2 * tf_S tf_pq_dist = tf.sqrt(tf_pq_sq_dist) tf_pp_dist = tf.sqrt(tf_pp_sq_dist) tf_surface_dist_sq = (tf_pp_dist - tf.ones(n, dtype=tf.float64)) ** 2 tf_rec_pq_dist = 1 / (tf_pq_dist + tf.eye(n, dtype=tf.float64)) - tf.eye(n, dtype=tf.float64) L_tf = (tf.reduce_sum(tf_rec_pq_dist) / 2 + k * tf.reduce_sum(tf_surface_dist_sq)) / n glob_init = tf.local_variables_initializer() #     with tf.Session() as tf_s: #     glob_init.run() #   res, = tf_s.run([L_tf], feed_dict={tf_x: x}) #   print(res) 

قارن أداء هذه الأساليب الثلاثة:

ن	الثعبان	جامع	pytorch	tensorflow
2000	4.03	0.083	1.11	0.205
10،000	99	2.82	2.18	7.9

الحسابات الموجهة تعطي ربحًا بأكثر من ترتيب ونصف عشري بالنسبة لرمز الثعبان الخالص. "لوح المرجل" في pytorch مرئي: تستغرق الحسابات ذات الحجم الصغير وقتًا ملحوظًا من الوقت ، لكنها لا تتغير تقريبًا مع زيادة حجم الحسابات.

التصور

في الوقت الحاضر ، يمكن تصور البيانات باستخدام عدد كبير من الحزم ، مثل Matlab و Wolfram Mathematica و Maple و Matplotlib وما إلى ذلك. في هذه الحزم هناك الكثير من الوظائف المعقدة التي تؤدي أشياء معقدة. لسوء الحظ ، إذا واجهت مهمة بسيطة ولكنها غير قياسية ، فستجد نفسك غير مسلح. الحل المفضل في هذه الحالة هو povray. هذا برنامج قوي جدًا يستخدم عادةً لإنشاء صور واقعية ، ولكن يمكن استخدامه كـ "مجمّع للمرئيات". عادةً ، بغض النظر عن مدى صعوبة السطح الذي تريد عرضه ، اطلب من povray فقط رسم مجالات بها مراكز ملقاة على هذا السطح.

باستخدام مكتبة vapory ، يمكنك إنشاء مشهد povray مباشرة في python وعرضه والنظر إلى النتيجة. الآن يبدو هذا:

يتم الحصول على الصورة على النحو التالي:

 import vapory from PIL import Image def create_scene(moment): angle = 2 * math.pi * moment / 360 r_camera = 7 camera = vapory.Camera('location', [r_camera * math.cos(angle), 1.5, r_camera * math.sin(angle)], 'look_at', [0, 0, 0], 'angle', 30) light1 = vapory.LightSource([2, 4, -3], 'color', [1, 1, 1]) light2 = vapory.LightSource([2, 4, 3], 'color', [1, 1, 1]) plane = vapory.Plane([0, 1, 0], -1, vapory.Pigment('color', [1, 1, 1])) box = vapory.Box([0, 0, 0], [1, 1, 1], vapory.Pigment('Col_Glass_Clear'), vapory.Finish('F_Glass9'), vapory.Interior('I_Glass1')) spheres = [vapory.Sphere( [float(r[0]), float(r[1]), float(r[2])], 0.05, vapory.Texture(vapory.Pigment('color', [1, 1, 0]))) for r in x] return vapory.Scene(camera, objects=[light1, light2, plane, box] + spheres, included=['glass.inc']) for t in range(0, 360): flnm = 'out/sphere_{:03}.png'.format(t) scene = create_scene(t) scene.render(flnm, width=800, height=600, remove_temp=False) clear_output() display(Image.open(flnm)) 

من مجموعة من الملفات ، يتم تجميع صور gif المتحركة باستخدام ImageMagic:

 convert -delay 10 -loop 0 sphere_*.png sphere_all.gif 

على github يمكنك رؤية رمز العمل ، وترد أجزاء منه هنا. في المقالة الثانية ، سأتحدث عن كيفية البدء في التقليل من الوظيفة بحيث تخرج النقاط من المكعب وتنتشر بالتساوي عبر المجال.