هناك عدد من المهام التي يجب أن يكون نطاق قيم الإخراج فيها محدودًا ، بينما لا يمكن لبيانات الإدخال ضمان ذلك. بالإضافة إلى المواقف القسرية ، يمكن أن يكون الحد من الإشارة مهمة موجهة نحو الهدف ، على سبيل المثال ، عند ضغط إشارة أو تنفيذ تأثير "تجاوز السرعة".
أبسط تطبيق للقيد هو إجباره على قيمة معينة إذا تم تجاوز مستوى معين. على سبيل المثال ، بالنسبة للجيوب الأنفية ذات السعة المتزايدة ، ستبدو كما يلي:

هنا ، تعمل وظيفة Clip كمحدد ، كحجة يتم من خلالها إرسال إشارة الإدخال ومعلمات التقييد ، وتكون نتيجة الوظيفة هي إشارة الخرج.
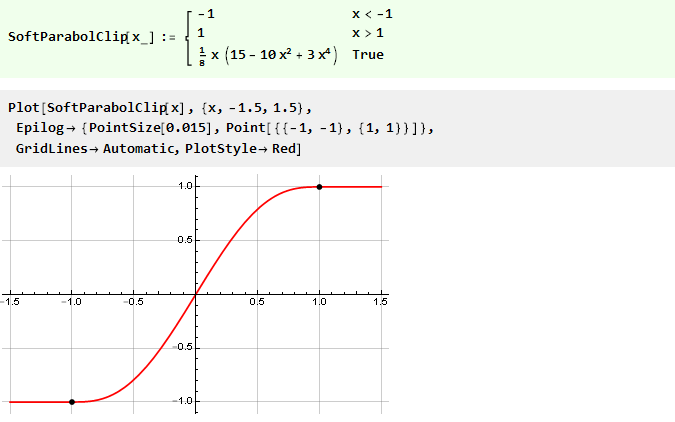
دعونا نلقي نظرة على الرسم البياني لوظيفة القصاصة بشكل منفصل:
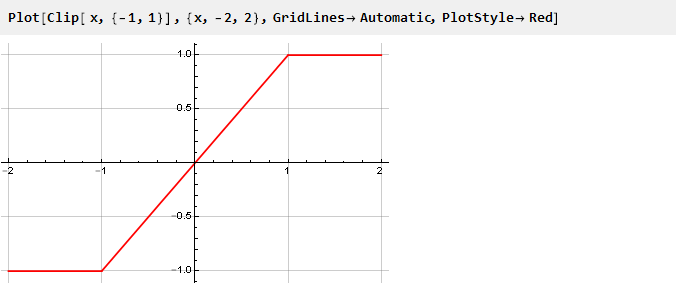
يمكن ملاحظة أنه في حين أننا لا نتجاوز حدود الحد ، فإن قيمة الإخراج تساوي المدخلات ولا تتغير الإشارة ؛ عند تجاوزها ، لا تعتمد قيمة الإخراج على الإدخال بأي شكل من الأشكال وتظل عند نفس المستوى. في الواقع ، لدينا وظيفة متواصلة مجزأة تتكون من ثلاث وظائف أخرى: y = -1 ، y = x و y = 1 ، تم تحديدها اعتمادًا على الوسيطة ، وتعادل الرموز التالية:

يحدث الانتقال بين الوظائف بشكل مفاجئ ؛ وتبدو مغرية لجعلها أكثر سلاسة. رياضيا ، ترجع هذه الحدة إلى حقيقة أن مشتقات الدوال عند نقاط الالتحام لا تتزامن. من السهل رؤية ذلك عن طريق رسم مشتق لوظيفة Clip:
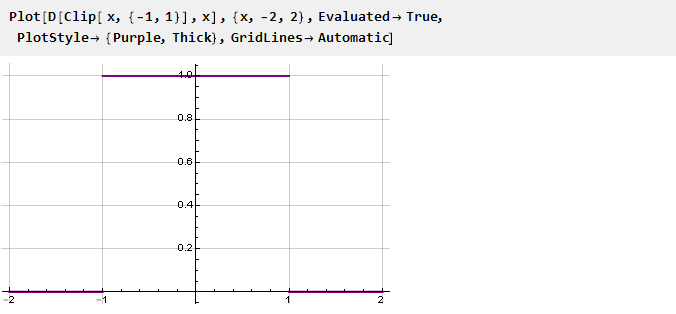
وبالتالي ، من أجل ضمان سلاسة وظيفة القيد ، من الضروري ضمان المساواة في المشتقات عند نقاط الالتحاق. وبما أن الدوال المتطرفة التي لدينا هي ثوابت ، ومشتقاتها تساوي صفر ، فيجب أن تكون وظائف التقييد المشتقة عند نقاط الالتحام مساوية للصفر. بعد ذلك ، سننظر في العديد من هذه الوظائف التي تضمن الإرساء السلس.
الجيوب الأنفية
إن أبسط شيء هو استخدام دالة sin على الفاصل الزمني من -pi / 2 إلى pi / 2 ، عند حدودها تكون قيم المشتق مساوية للصفر حسب التعريف:
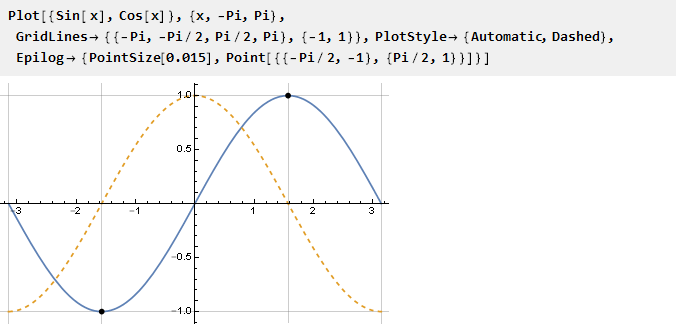
ما عليك سوى قياس الحجج بحيث يتم عرض الوحدة على Pi / 2. الآن يمكننا تحديد دالة الإحاطة نفسها:

وبناء جدولها الزمني:
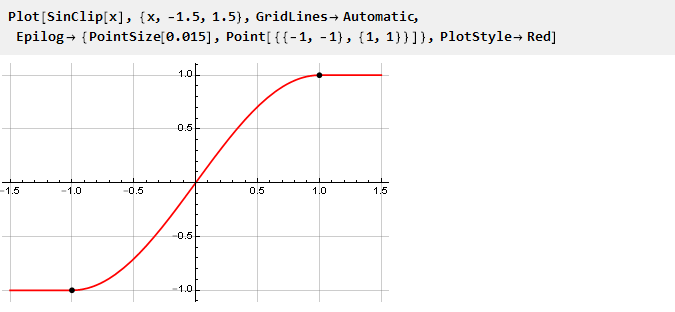
نظرًا لأن حدود تقييدنا محددة بدقة ، يتم تعيين التقييد عن طريق تغيير حجم إشارة الإدخال مع إعادة قياس لاحقة (إذا لزم الأمر).
لم يعد هناك أيضًا وضع يتم فيه إرسال إشارة الإدخال إلى الإخراج بدون تشويه - كلما انخفض مستوى الكسب ، انخفض مستوى التشويه بسبب القيد - ولكن الإشارة مشوهة في أي حال.
يمكن أيضًا رؤية تأثير معلمة الكسب على تشويه الإشارة في الديناميكيات:

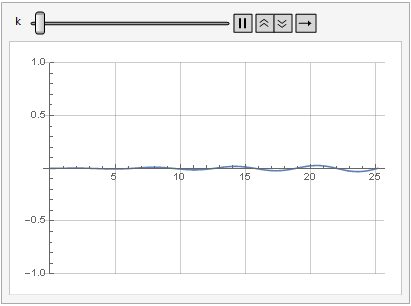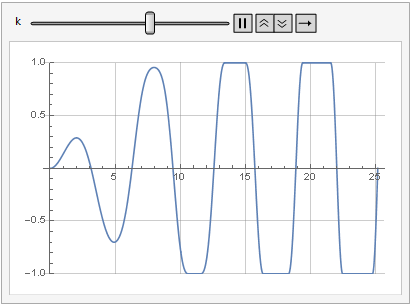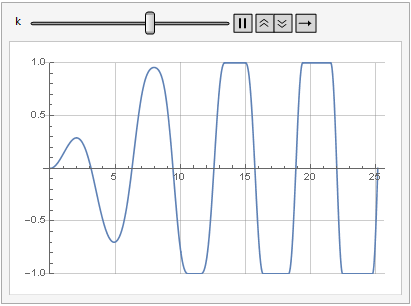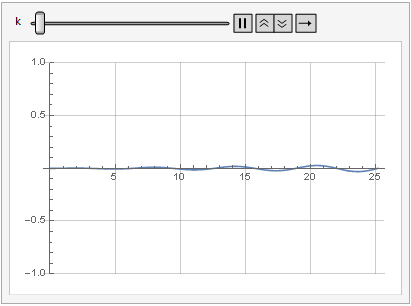
نعومة أكثر
دعونا نلقي نظرة على مشتق وظيفتنا:
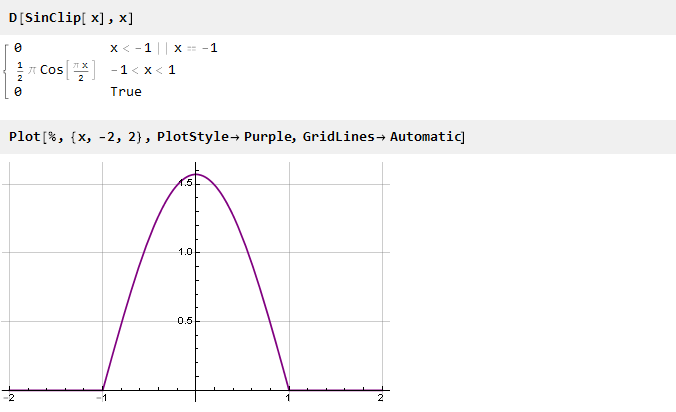
لم يعد هناك فجوات في القيم ، ولكن هناك فجوات في المشتق (الثاني ، إذا قمنا بالعد من الوظيفة الأصلية). من أجل القضاء عليه ، يمكنك الذهاب في الاتجاه المعاكس - أولاً تكوين مشتق سلس ، ثم دمجها للحصول على الوظيفة المطلوبة.
أسهل طريقة لإبطال المشتق عند النقطتين 1 و 1 هي ببساطة تربيع الدالة - كل القيم السالبة للدالة ستصبح موجبة ، وبالتالي ، ستحدث الانحرافات عند نقاط تقاطع الدالة بصفر.
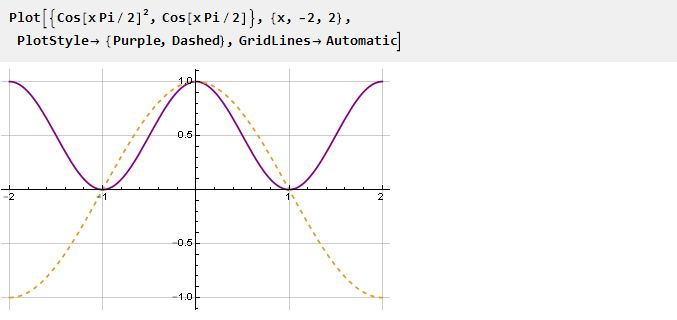
ابحث عن المشتق:
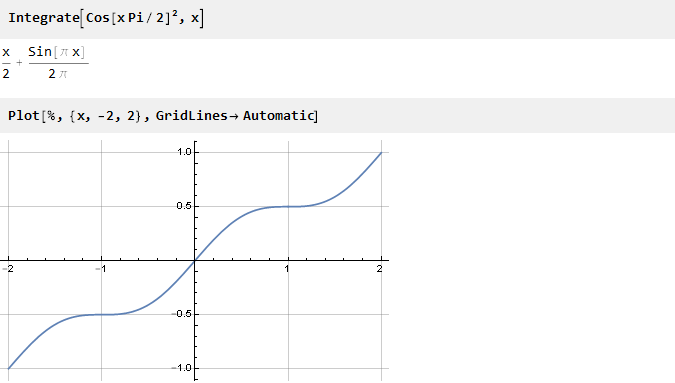
الآن يبقى قياسه على طول المحور الإحداثي. للقيام بذلك ، ابحث عن قيمته عند النقطة 1:

والقسمة عليه (نعم ، هنا بالتحديد هو الضرب الأولي على 2 ، لكن هذا لا يحدث دائمًا):

وبالتالي ، ستتخذ وظيفة التقييد النهائية الشكل التالي:
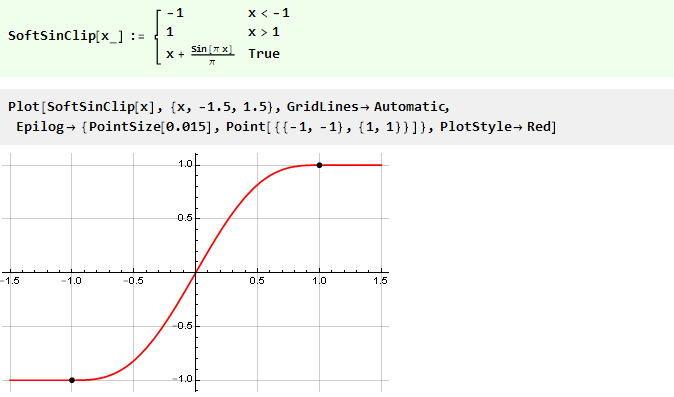
ننتقل إلى كثيرات الحدود
يمكن أن يكون استخدام الدوال المثلثية في بعض الحالات مسرفًا إلى حد ما. لذلك ، سنحاول بناء الوظيفة التي نحتاجها ، مع البقاء في إطار العمليات الرياضية الأولية.
النظر في القطع المكافئ:
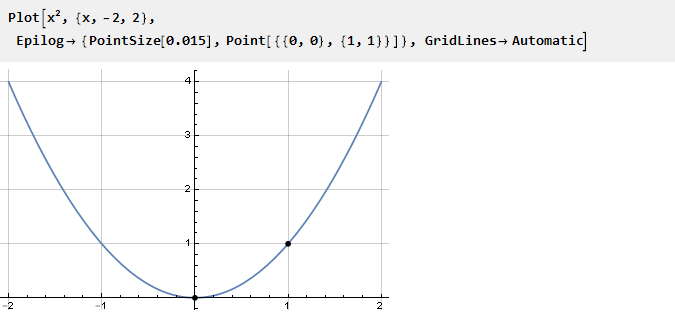
نظرًا لأنه يحتوي بالفعل على انعطاف عند النقطة صفر ، يمكننا استخدام نفس الجزء على الفاصل الزمني {0،1} للإرساء مع الثوابت. بالنسبة للقيم السالبة ، يجب إزالته إلى اليسار وإلى اليسار:

وللإيجابية - تعكس عموديا وأفقيا:

وستتخذ وظيفتنا مع القطع المكافئ الشكل:
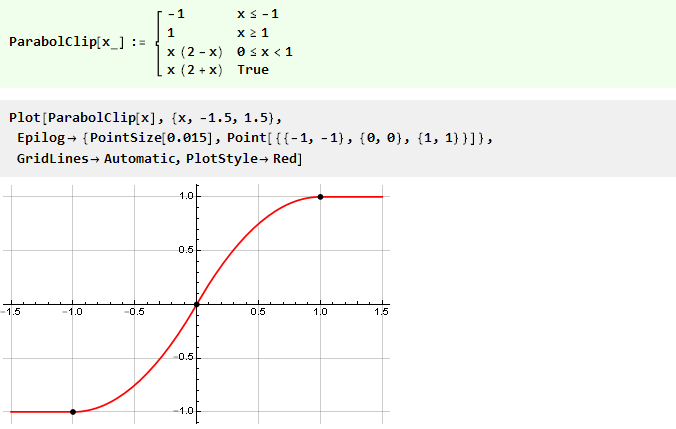
دعونا نعقد قليلا
دعنا نعود إلى القطع المكافئ الخاص بنا ، وقم بقلبه وتحويله لأعلى وحدة واحدة:
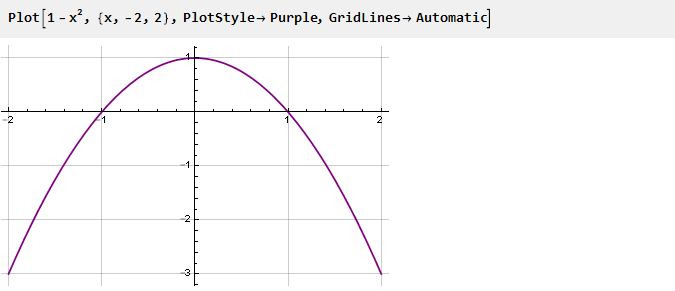
سيكون هذا مشتقًا لوظيفتنا. لجعلها أكثر سلاسة عند نقاط الالتحاق ، سنقوم بتربيع المشتقات الثانية بهذه الطريقة:
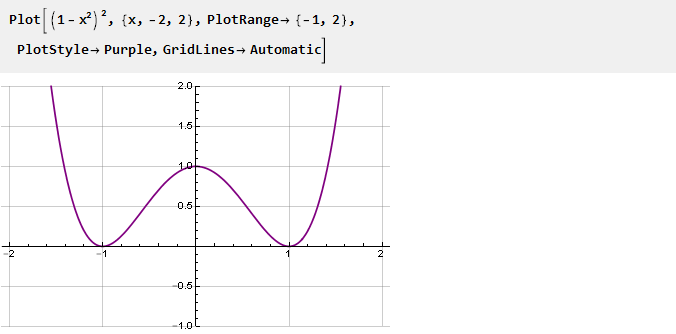
التكامل والقياس:

نحصل على وظيفة أكثر سلاسة:
المزيد من النعومة لإله النعومة
هنا نحاول تحقيق نعومة عند نقاط الالتحام على مشتقات أعلى. للقيام بذلك ، كبداية ، نحدد الدالة على أنها كثيرات الحدود مع معاملات غير معروفة ، ونحاول العثور على المعاملات من خلال حل لنظام المعادلات.
لنبدأ بالمشتق الأول:

ثانيًا:

ثالث:

تبدو جميع هذه المعاملات كما لو كان لديهم نوع من المنطق. نكتب العوامل ، ونضربها في قيمة الدرجة عند س ؛ ولكي لا نكتب نفس الشيء في كل مرة ، نقوم بأتمتة عملية العثور على المعاملات:
 يبدو أن
يبدو أن المعاملات ذات الحدين. نحن نفترض جريئة أنهم ، وعلى هذا الأساس ، نكتب الصيغة العامة:

تحقق:
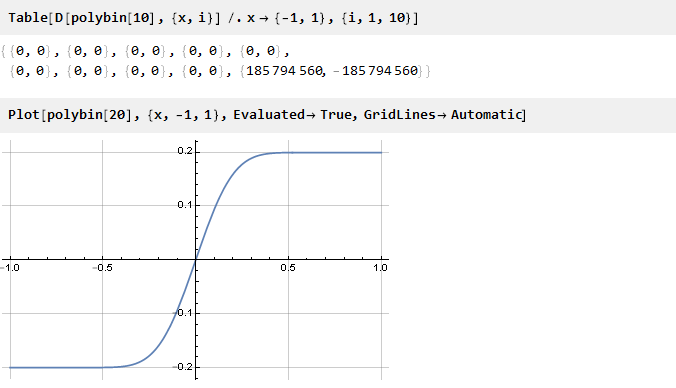
يبدو أن هذا صحيح
[1] . يبقى فقط لحساب عامل المقياس لتحقيق الحواف للوحدة:

وبعد القياس والتبسيط ، نجد أن معرفتنا بالرياضيات قديمة إلى حد ما
[2] :
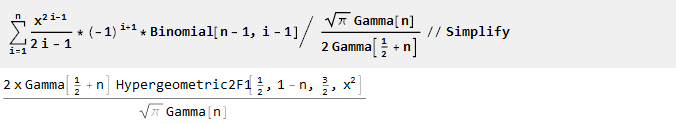
وهكذا ، حصلنا على دالة مولدة للترتيب n تكون فيها n-1 من المشتقات الأولى مساوية للصفر:

دعنا نرى ما حدث:
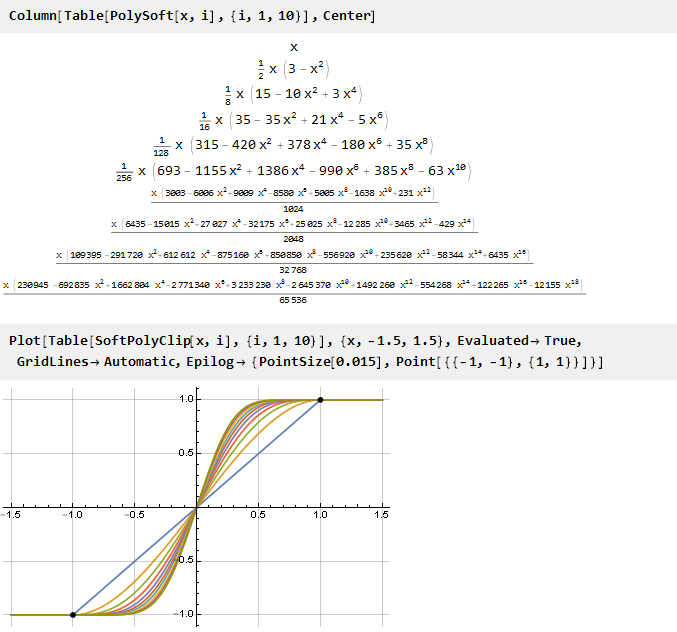
وبما أن صيغتنا المعممة تبين أنها مستمرة ، يمكنك استخدام قيم معلمات غير صحيحة إذا كنت ترغب في:
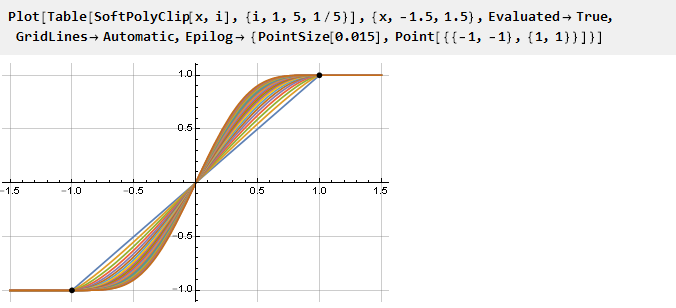
يمكنك أيضًا إنشاء رسوم بيانية للمشتقات مخفضة إلى مقياس واحد:
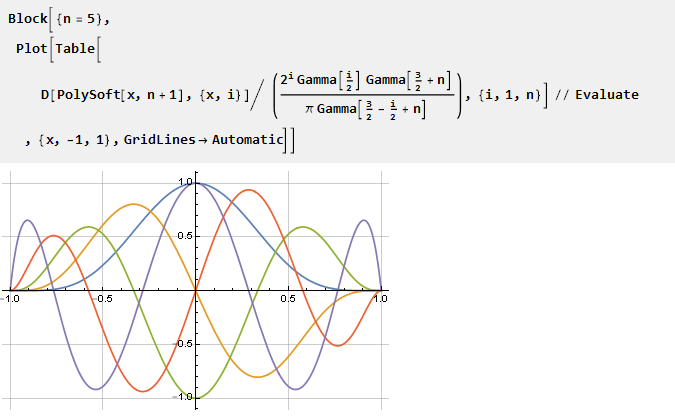
أضف صلابة
سيكون من المغري أن تكون قادرًا على ضبط درجة "صلابة" التقييد.
دعونا نعود إلى القطع المكافئ المقلوب لدينا وإضافة معامل عند الدرجة x:

كلما كانت n أكبر ، كلما كان مشتقنا أكبر "مربع" ، ومشتقاته الحادة ، على التوالي:
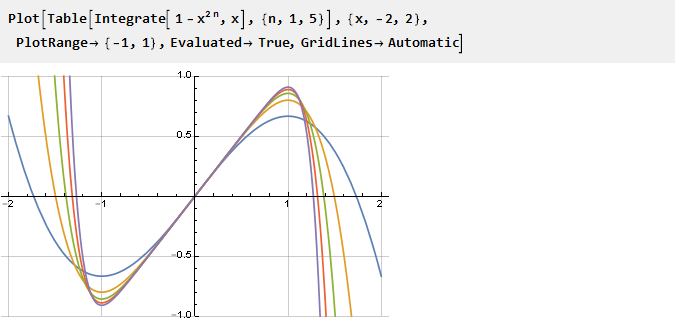
نحسب المضاد للمشتقات ونعدل المقياس:

الآن دعنا نحاول تعيين الخطوة الكسرية للمعلمة:
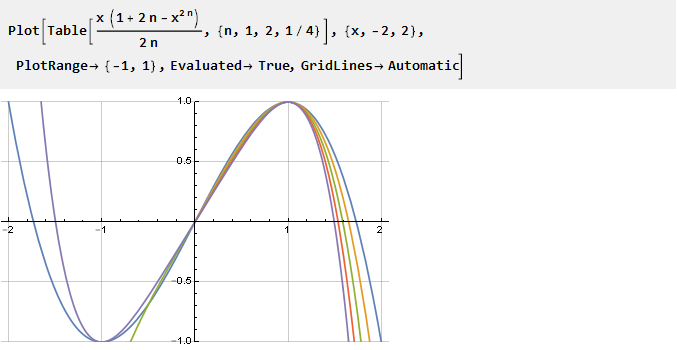
كما ترى ، ليس كل n لديه الحل الصحيح في الجزء السلبي ، ولكن الشروط اللازمة لنا لا تزال مستوفاة في الجزء الصحيح (الإيجابي) - لذلك ، بالنسبة للقيم السلبية ، يمكننا ببساطة استخدامه معكوسًا بحجة معكوسة. وبما أن مجال تعريف المعلمة لم يعد يقتصر فقط على الأعداد الصحيحة الموجبة ، يمكننا تبسيط الصيغة عن طريق استبدال 2n ب n:

واستبدال n بـ n-1 ، يمكنك جعل الصيغة أجمل قليلاً:
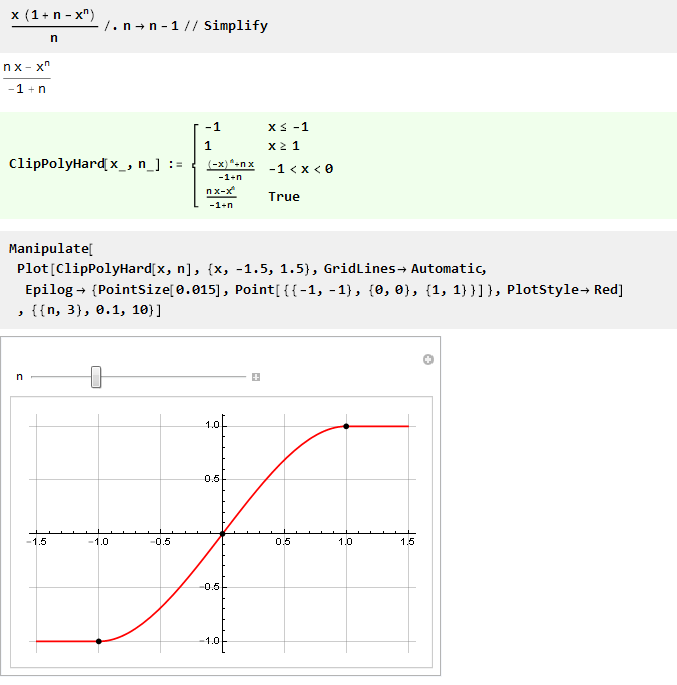
نظرًا لأن n تساوي واحدًا نحصل على القسمة على صفر ، ثم حاول إيجاد الحد:

تم العثور على الحد ، مما يعني أنه يمكننا الآن إضافة
[3] وظيفة n إلى 1 والنظر فيها لجميع الأصفار الكبيرة n:
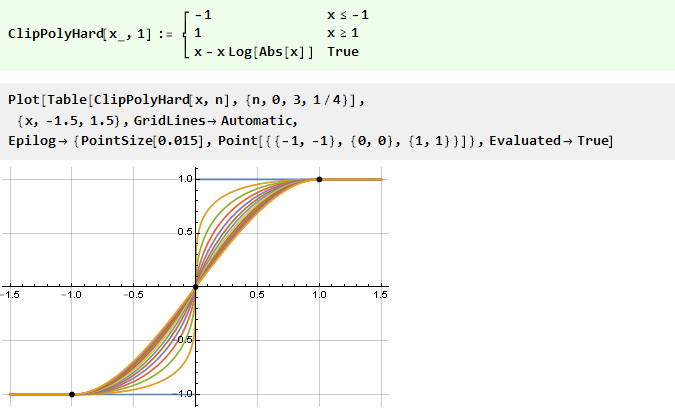
إذا قمنا في البداية بتربيع القطع المكافئ المقلوب ، فإننا نحصل على وظيفة أكثر سلاسة:
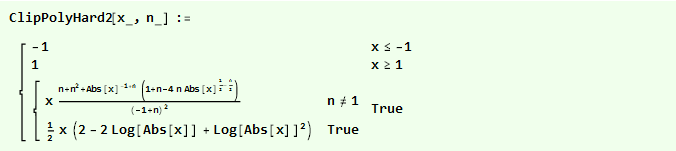
ويمكننا مقارنتها على مخطط واحد:
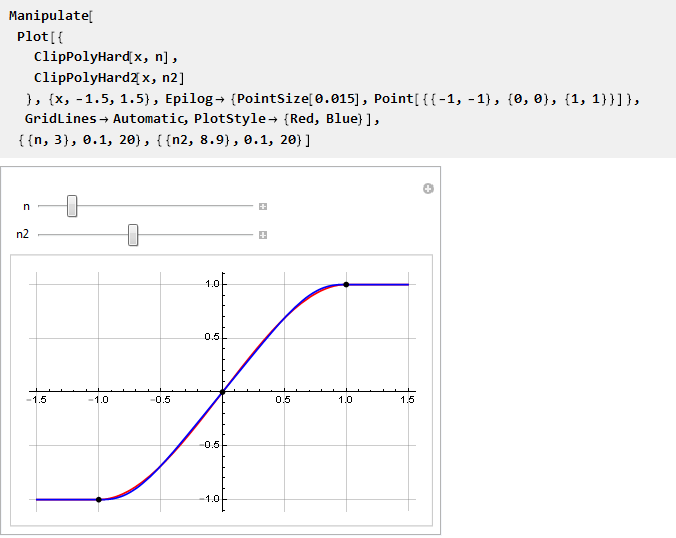
تبسيطها
دعونا نلقي نظرة على الوظيفة التالية:
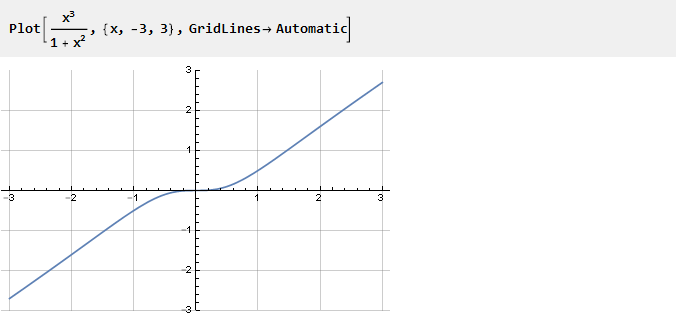
لم تظهر بالصدفة.
إذا قمت بإزالة وحدة منها ، فسوف ينكمش x
2 وسيبقى x فقط ، أي خط مائل. وبالتالي ، كلما كانت قيمة x أصغر ، كلما زاد تأثير الوحدة في المقام ، مما خلق الانحناء الذي نحتاجه. وبالنظر إلى هذه الوظيفة بمقاييس مختلفة ، يمكنك التحكم في درجة هذا الانحناء:

وبالتالي ، يمكننا إعادة كتابة الوظيفة السابقة باستخدام التحكم في الصلابة باستخدام حدود متعددة الحدود عقلانية من 3 ترتيب فقط:
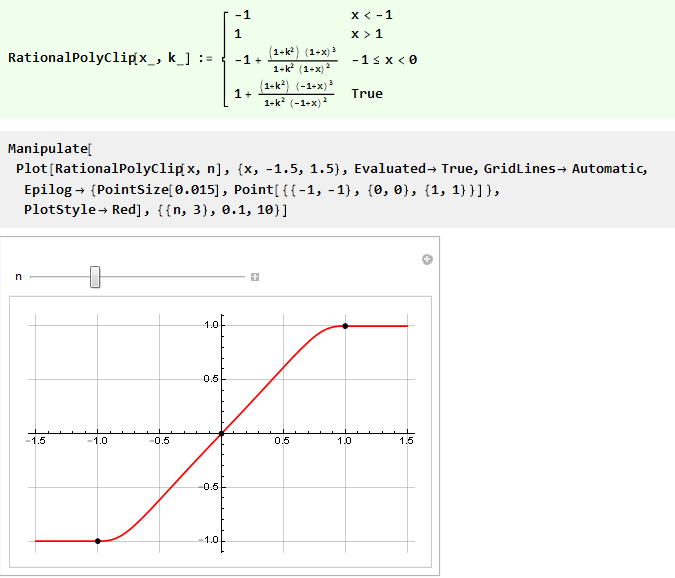
أتمتة
حتى لا نحدد الوظائف المتقطعة باستمرار في كل مرة ، يمكننا تحديد وظيفة مساعدة تقوم بذلك من تلقاء نفسها ، مع أخذ وظيفة مانح كحجة كمدخل.
إذا كانت وظيفتنا تحتوي بالفعل على تناظر قطري ومتوافقة مع مركز الإحداثيات (مثل موجة جيبية) ، فيمكننا ببساطة القيام بذلك
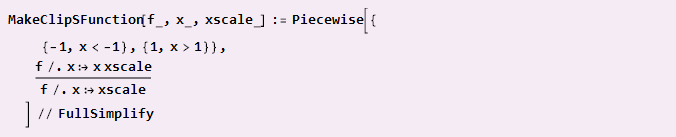
مثال للاستخدام:

إذا كنت بحاجة إلى التجميع من القطع ، كما هو الحال في القطع المكافئ ، ويحدد مركز الإحداثيات نقاط الالتحام ، فستكون الصيغة أكثر تعقيدًا قليلاً:
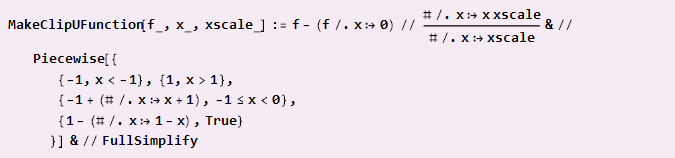
مثال للاستخدام:

دعنا ننتقل إلى العارضين
يمكن لأي وظيفة أن تكون مانحًا على الإطلاق لحل هذه المشكلة ، ما عليك سوى تزويدها بنقاط انعطاف. خذ ، على سبيل المثال ، الأس الذي تحول لأسفل بمقدار واحد:
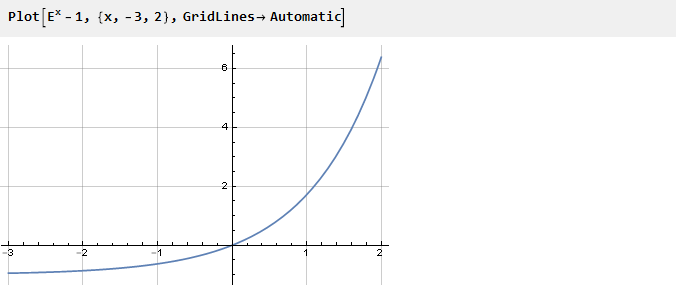
في السابق ، لضمان الانعطاف الضروري عند النقطة صفر ، قمنا بجمع الدالة. ولكن يمكنك الذهاب في الاتجاه الآخر - على سبيل المثال ، تلخيص بدالة أخرى يكون مشتقها عند النقطة صفر معاكسًا للإشارة من مشتق الأس. على سبيل المثال ، -x:
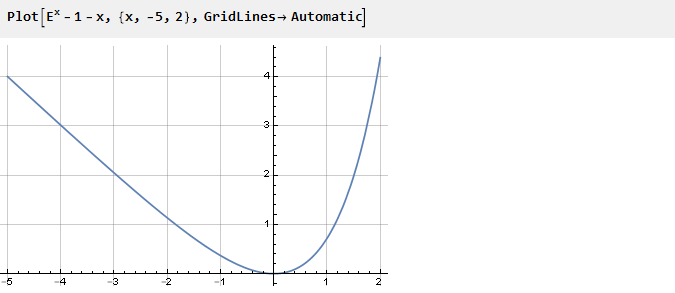
اعتمادًا على أي جانب سوف نأخذ المنحنى ، سيعتمد الشكل النهائي للدالة عليه. الآن ، باستخدام الوظيفة الإضافية المحددة مسبقًا واختيار أحد الجوانب ، نحصل على:

إما

والآن يمكننا مقارنتها على مخطط واحد:
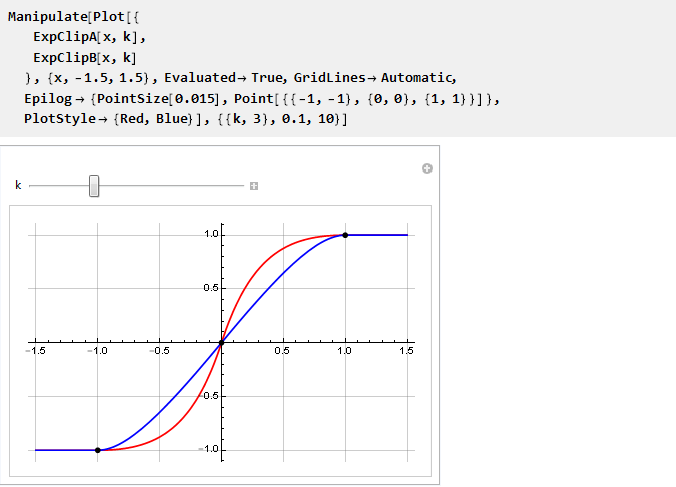
من الواضح أن k → 0 يميلون إلى التطابق ؛ وبما أننا لا نستطيع حساب قيمهم مباشرة ، نظرًا لأننا نحصل على القسمة على صفر ، فسوف نستخدم الحد:

وحصلوا على وظيفة مجردة من القطع المكافئ المعروف لنا بالفعل.
كسر التماثل
حتى الآن ، كنا ندرس الوظائف المتماثلة حصريًا. ومع ذلك ، هناك أوقات لا نحتاج فيها إلى التناظر - على سبيل المثال ، لمحاكاة التشوهات في صوت مضخمات الأنبوب.
خذ الأس واضربه بمربع القطع المكافئ المقلوب - للحصول على التقاطع مع محور الخراج عند النقطتين 1 و 1 ، وفي نفس الوقت ضمان سلاسة المشتق الثاني ؛ المعلمة ممكنة من خلال تحجيم حجة الأسي:
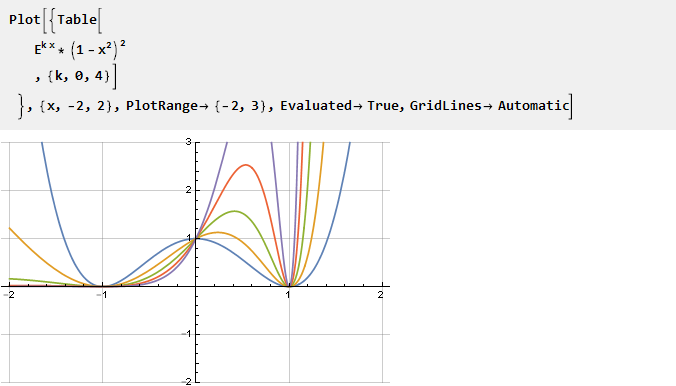
ابحث عن المشتق وقابله:
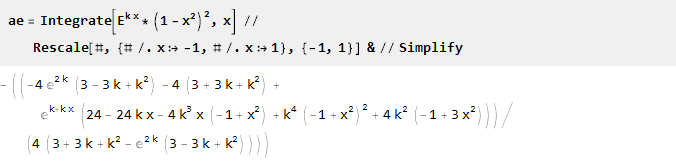
بما أن k = 0 نحصل على القسمة على صفر:

ثم نجد أيضًا الحد ،

وهو كثير حدود سلس من الدرجة الثالثة المعروفة لنا بالفعل. الجمع بين كل شيء في وظيفة واحدة ، نحصل
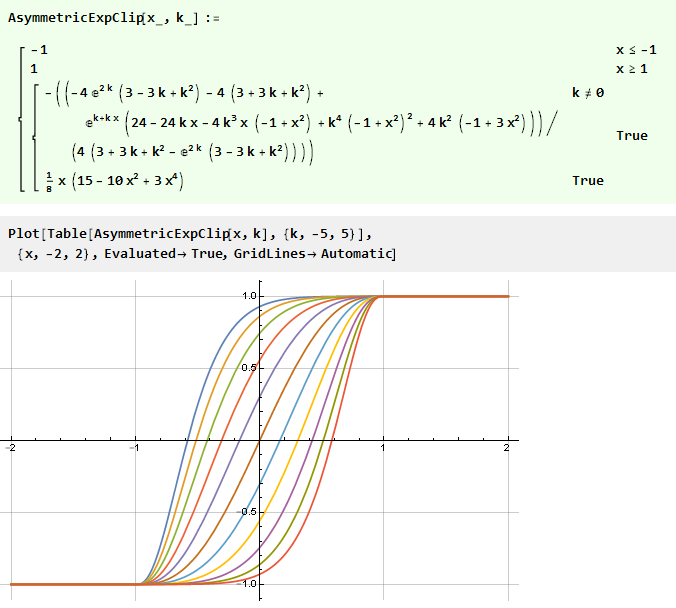
بدلاً من تصميم دالة غير متماثلة مبدئيًا ، يمكنك السير في الاتجاه الآخر - استخدام التناظر الجاهز ، ولكن "ثني" قيمة هذه الوظيفة باستخدام دالة منحنى إضافية محددة على الفاصل الزمني {-1،1}.
خذ بعين الاعتبار ، على سبيل المثال ، الغلو:
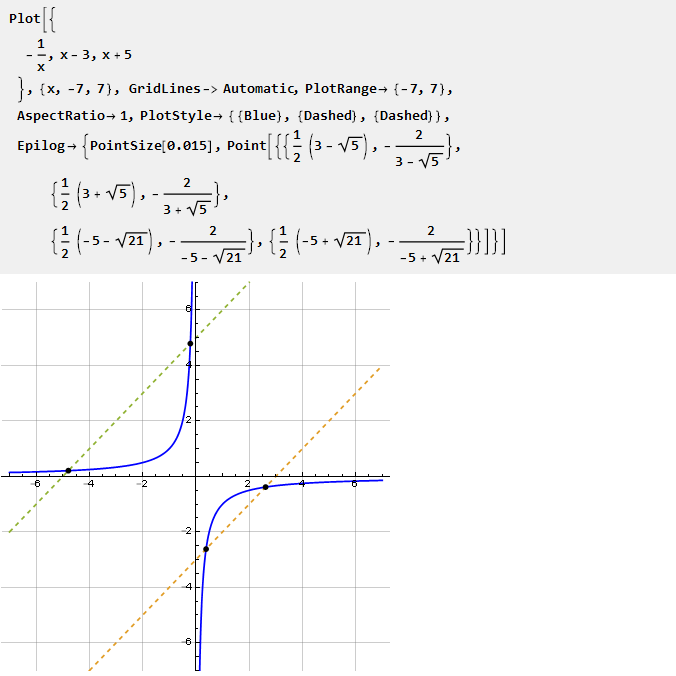
بالنظر إلى الجزء الخاص به بمقاييس مختلفة ، يمكنك ضبط درجة الانحناء في كلا الاتجاهين. كيف تجد هذا الجزء؟ استنادًا إلى الرسم البياني ، يمكن للمرء أن يبحث عن تقاطع القطع الزائد مع الخط. ومع ذلك ، نظرًا لأن مثل هذا التقاطع لا يوجد دائمًا ، فإن هذا يخلق بعض الصعوبات. لذلك ، سنذهب في الاتجاه الآخر.
أولاً ، أضف عوامل التحجيم إلى القطع الزائد:

ثم سنقوم بإنشاء نظام من المعادلات التي تحدد شروط مرور القطع الزائد من خلال نقاط معينة - وسيعطي حلها المعاملات التي تهمنا:

الآن استبدل الحل في الصيغة الأصلية وقم بتبسيط:

دعونا نرى ما نحصل عليه ، اعتمادًا على المعلمة k:
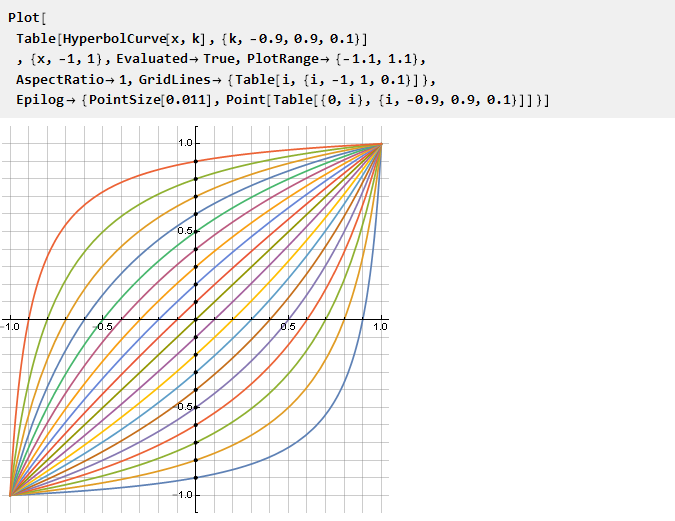
من الجدير بالذكر أنه بالنسبة لـ k = 0 ، تنهار الصيغة بشكل طبيعي عند x ولا تحدث حالات خاصة - على الرغم من الإشارة إلى المبالغة الأولية ، فإن هذا يعادل مقطعًا بطول صفري ، واثنين في وقت واحد. ليس أقل ملحوظة أن الوظيفة المعكوسة لها هي نفسها ، ولكن مع المعلمة السلبية k:

يمكننا الآن استخدامه لتعديل وظيفة القيد التعسفي ، وبالتالي فإن المعلمة k تحدد نقطة التقاطع مع المحور المنسق:
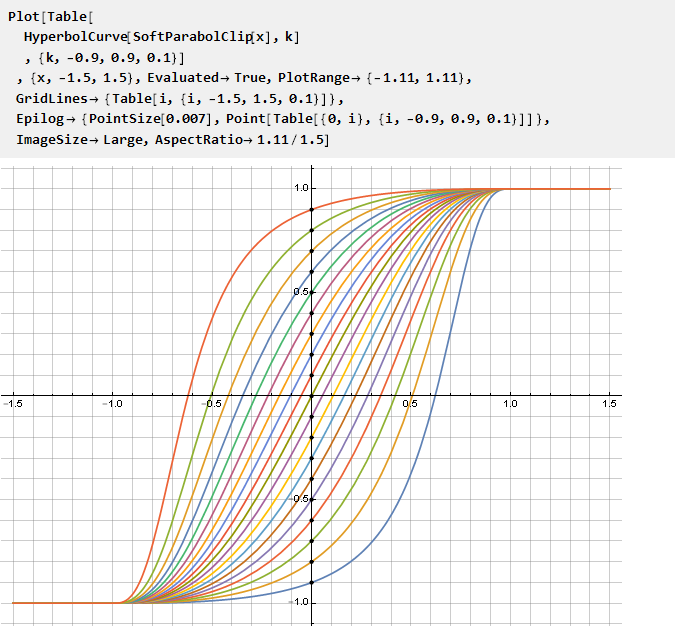
وبالمثل ، يمكنك بناء منحنيات من وظائف أخرى ، على سبيل المثال ، قانون السلطة بقاعدة متغيرة:
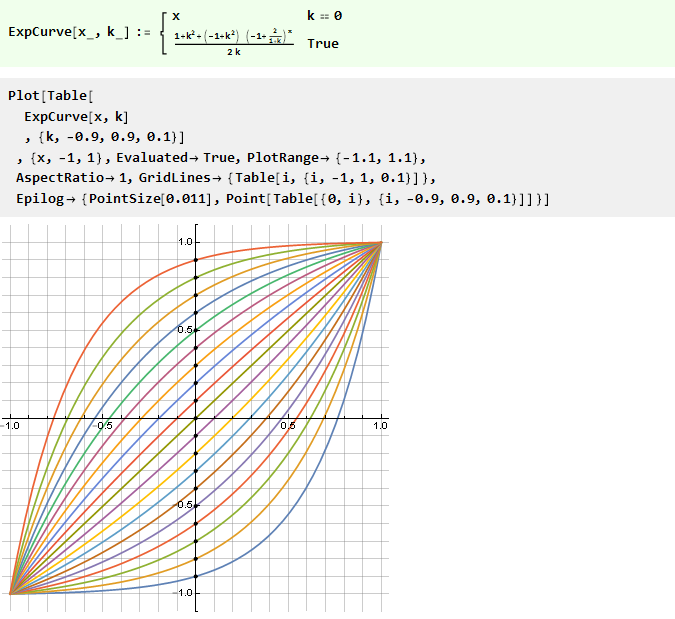
أو معكوسها لوغاريتمي:
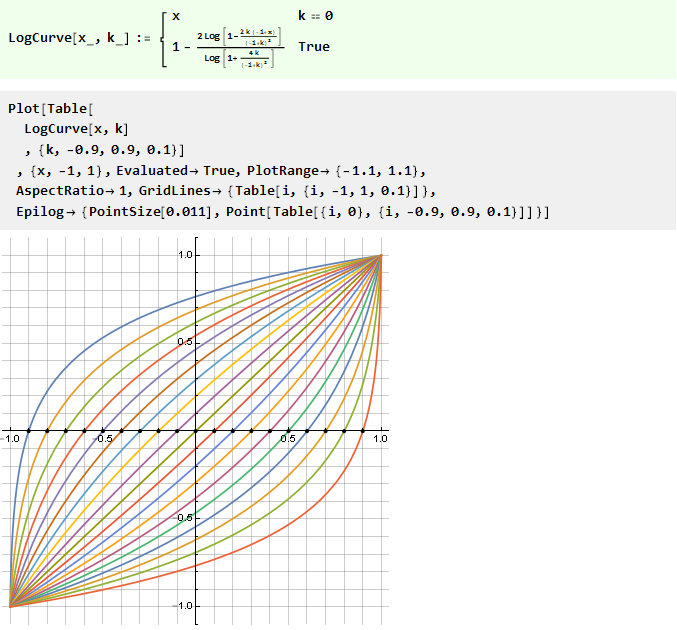
تحتاج إلى مزيد من الدقة
قد نرغب في الحصول على تباعد خطي مضمون لوظيفة على فاصل زمني معين. هذا أمر منطقي للتنظيم من خلال إدخال خط مستقيم في وظيفة مستمرة متقطعة ،
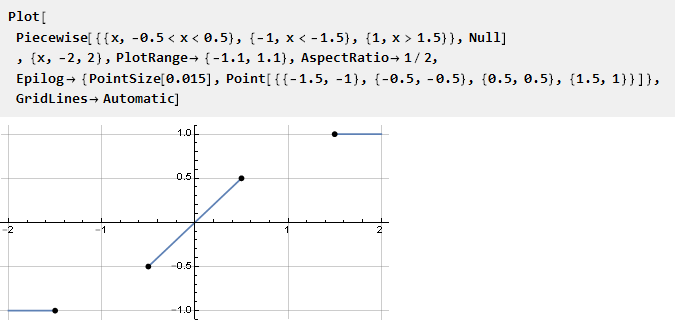
مساحات فارغة تحتاج فيها لملء بعض الوظائف. من الواضح ، من أجل الالتحام السلس مع القسم الخطي ، يجب أن يكون مشتقها الأول مساوياً للوحدة ؛ وجميع الصفر اللاحق (إن أمكن). لكي لا نستنتج مثل هذه الوظيفة من جديد ، يمكننا أخذ وظيفة جاهزة وتكييفها مع هذه المهمة. يمكنك أيضًا ملاحظة أن النقاط القصوى تقع أبعد قليلاً من الوحدة - وهذا ضروري للحفاظ على ميل القسم الخطي.
خذ وظيفة PolySoft المشتقة سابقًا وقم بتحويلها حتى نحصل على واحدة في مركز الإحداثيات:
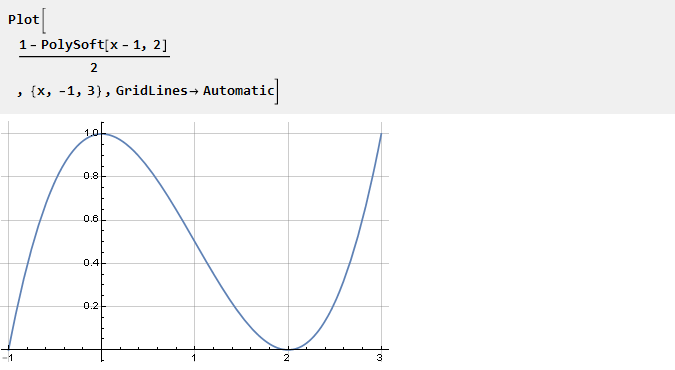
يستنتج من خصائصه أن n-1 للمشتقات اللاحقة عند النقطتين 0 و 2 ستكون مساوية للصفر:
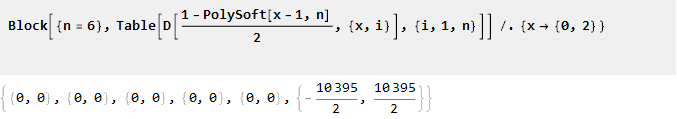
الآن دمجها:
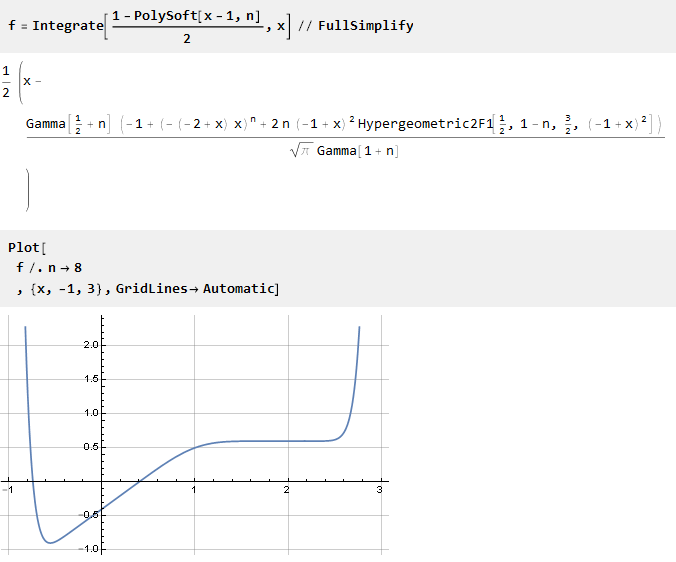
تم تحويل الوظيفة لأسفل بالنسبة لمحور الخراج. لذلك ، من الضروري إضافة ثابت (يساوي قيمة الوظيفة عند النقطة 0) من أجل دمج مراكز الإحداثيات:

هنا لدينا صفر في درجة ن. لم تنخفض ، حيث لم يتم تحديد قيمة الصفر في درجة الصفر ؛ يمكننا حذفه يدويًا ، أو ، في التبسيط ، يمكننا أن نوضح بشكل صريح أن n أكبر من الصفر:

سنقوم بالتحقق فقط في حالة. القيمة عند النقطتين 0 و 2 لجميع n:

مشتقات عند حواف الفترة (لثنائي الحدود من النظام 5):

كما ترون ، اتضح أن الوظيفة مرهقة إلى حد ما. من أجل عدم سحبها وعدم تعقيد الحسابات ، سنستمر في التلاعب باستخدام كثيرات الحدود ، على سبيل المثال ، الترتيب الرابع:

والآن يمكنك من خلاله ملء المساحة الحرة:

تحقق:
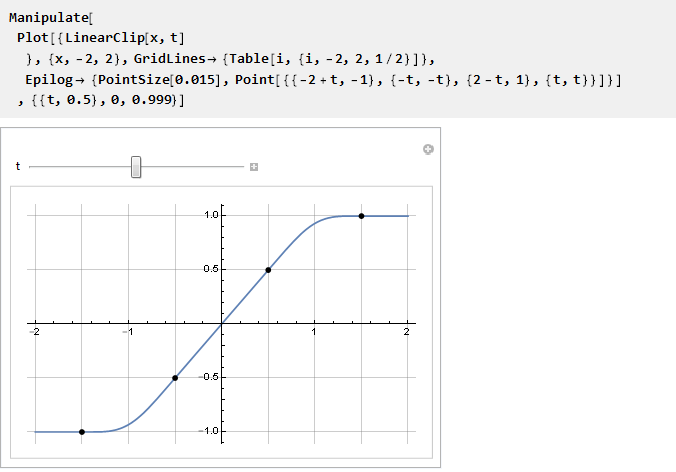
نذهب إلى ما لا نهاية
في بعض الأحيان قد تكون هناك حاجة إلى وظائف تميل إلى وحدة ولكنها لا تصل إليها.
تقترح ويكيبيديا عدة حلول معروفة:
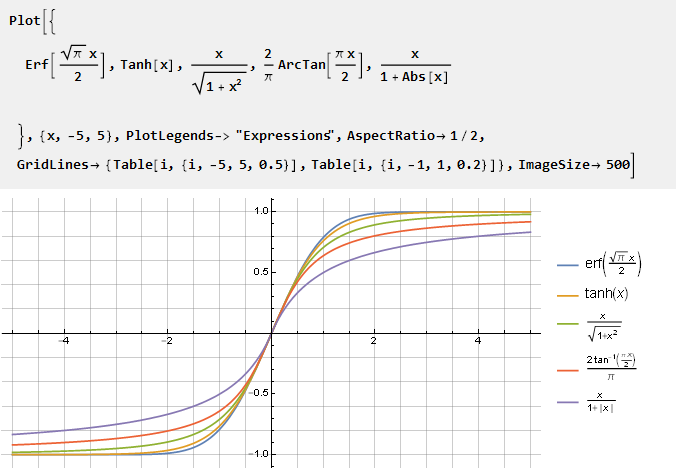
نظرًا لأن هذه الوظائف لا تصل إلى الوحدة ، فمن الأكثر ملاءمة تطبيعها فيما يتعلق بالمشتق في مركز الإحداثيات.
يمكننا تعديل شكل هذه الوظائف من خلال حجة باستخدام بعض الوظائف المتناظرة قطريًا ، على سبيل المثال:
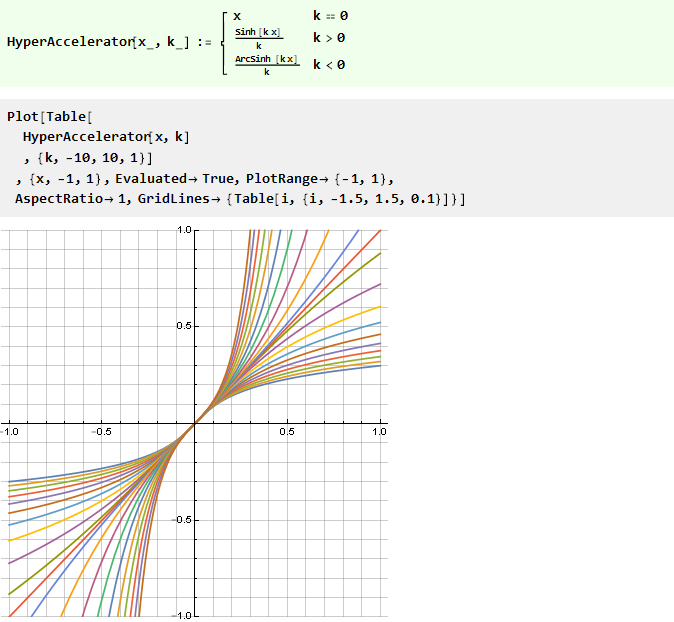
هذه الوظيفة ، بالمناسبة ، معكوسة أيضًا ، أي
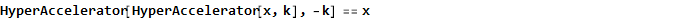
وكما ينطبق على ظل الزاوية ، على سبيل المثال ، نحصل عليه
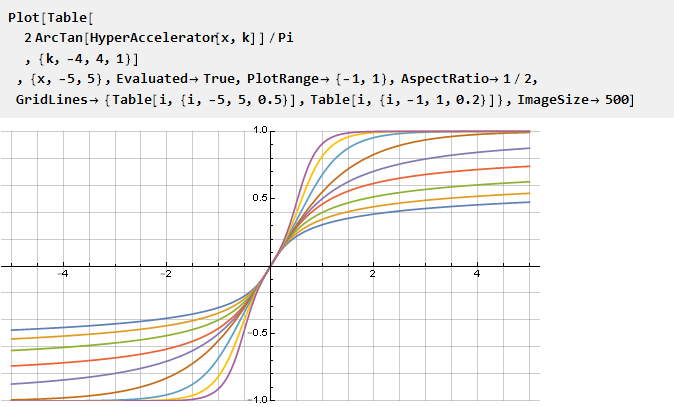
والتي ، على وجه الخصوص ، مع المعلمة k = 1
ستعطينا وظيفة Guderman .
كما ترون ، مع هذا النهج ، يمكن الحصول على مكامن الخلل غير المرغوب فيها ، لذلك من الأفضل التحكم في صلابة القيد مباشرة من خلال خاصية الوظيفة نفسها. خذ بعين الاعتبار العديد من هذه الوظائف مع معلمة ، يتم حذف نتيجتها للإيجاز.
من وظيفة الطاقة:
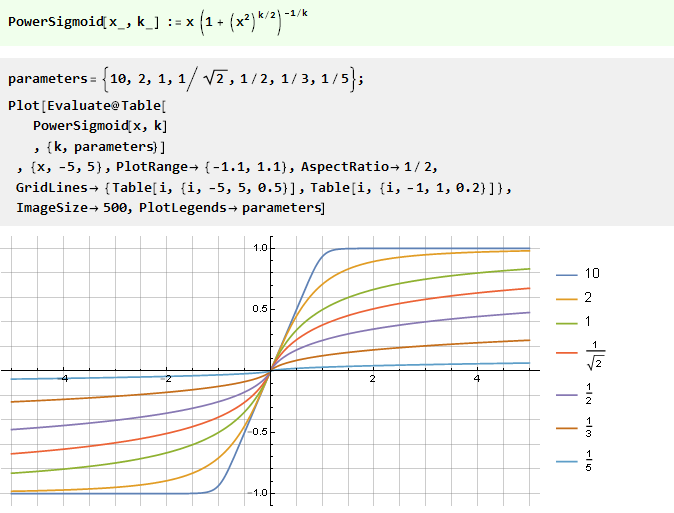
من مجموع وظيفتين على شكل حرف V مع إزاحة:
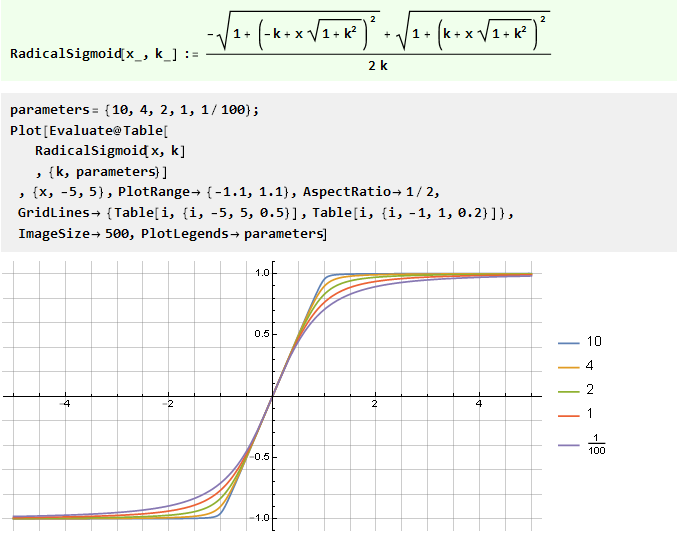
من دالة الخطأ المعممة:
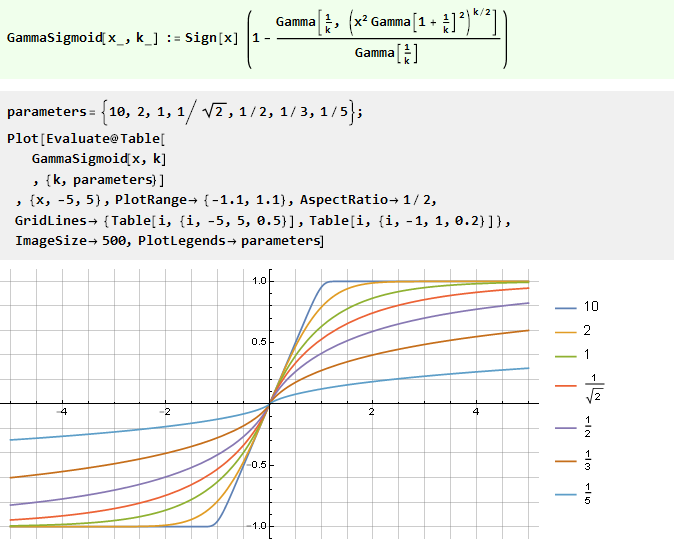
دمج كثيرات الحدود العقلانية:
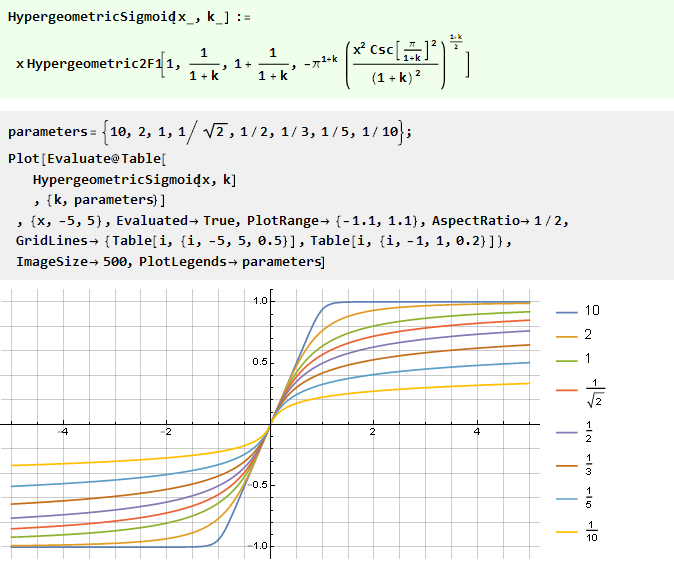
ومن المثير للاهتمام أن حالتها الخاصة ظل ظل:

الخلاصة
يمكن أن يكون بناء مثل هذه الوظائف مهمة رائعة ، يتم خلالها الحصول على صيغ بسيطة ومعقدة ، جميلة وليست للغاية. قد يبدو أنهم جميعًا متشابهون جدًا مع بعضهم البعض ولا توجد حاجة لمثل هذا التنوع. ليس هذا هو الحال بالضرورة.
يمكن أن يكون الفرق أكثر وضوحًا في المقاييس الأخرى - على سبيل المثال ، اللوغاريتمية. بالإضافة إلى ذلك ، بالإضافة إلى المهام الموضحة في الرأس ، يمكن استخدام وظائف مماثلة أيضًا في مهام أخرى - خلط الإشارات ، عندما يتم الجمع بين التوهين السلس لإشارة واحدة مع الزيادة السلسة لإشارة أخرى ، أو بناء مرشحات صوتية - ومن ثم سيتم إدراك الفرق عن طريق الأذن ، أو لبناء التدرجات - وبعد ذلك يدرك الفرق بالعين. بالإضافة إلى ذلك ، يمكن استخدامها كمانحين لوظائف أخرى أكثر تعقيدًا - على سبيل المثال ،
النافذة .
في الختام ، يجدر توضيح بضع نقاط أخرى.
تم تحديد جميع الوظائف هنا في النطاق من -1 إلى 1. إذا كنت بحاجة إلى نطاق مختلف (على سبيل المثال ، من 0 إلى 1) ، فيمكن إعادة سردها إما يدويًا:
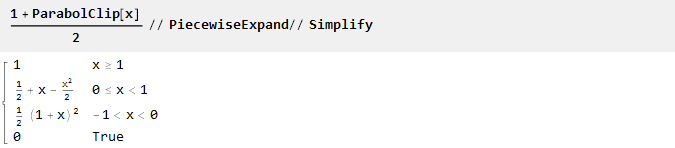
أو باستخدام وظيفة التكبير المدمجة:

ولتسهيل تصدير الصيغ التي تم الحصول عليها إلى رمز البرنامج ، قد تكون وظيفة CForm مفيدة:
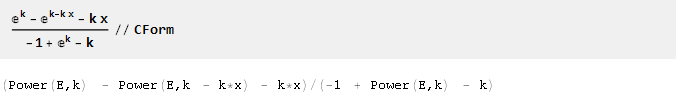
يمكن تنزيل مستند Mathematica المصدر
هنا .
ملاحظات:
[1] سوف يتمكن عالم الرياضيات الحقيقي بالتأكيد من إثبات (أو دحض) هذا البيان بدقة.
[2] لا تُدرج الدوال المفرطة في المسار القياسي للتحليل الرياضي.
[3] يتم تعريف هذا الحمل الزائد فقط لوحدة الأحرف ؛ لن يتم التعرف على وحدة بتنسيق فاصلة عائمة (على سبيل المثال ، عند رسم رسم بياني).