مرحبا حب.
إن موضوع "المربعات السحرية" مثير للاهتمام ، لأنه من ناحية ، كانت معروفة منذ العصور القديمة ، من ناحية أخرى ، فإن حساب "المربع السحري" حتى اليوم هو مهمة حسابية صعبة للغاية. تذكر ، من أجل إنشاء "المربع السحري" NxN ، تحتاج إلى إدخال الأرقام 1.NN N بحيث يكون مجموع أفقيتها وعموديها وأقطارها مساوياً لنفس الرقم. إذا قمت ببساطة بفرز عدد كل الخيارات لترتيب الأرقام لمربع 4x4 ، فسوف نحصل على 16! = 20،922،789،888،000 خيار.
ضع في اعتبارك كيف يمكن القيام بذلك بشكل أكثر كفاءة.

بادئ ذي بدء ، نكرر حالة المشكلة. تحتاج إلى ترتيب الأرقام في مربع بحيث لا تتكرر ، ويكون مجموع الخطوط والأعمدة والأقطار مساويًا لنفس الرقم.
من السهل إثبات أن هذا المبلغ هو نفسه دائمًا ، ويتم حسابه بواسطة الصيغة لأي n:
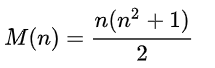
سننظر في مربعات 4x4 ، لذا فإن المجموع = 34.
قم بتدوين جميع المتغيرات بواسطة X ، سيبدو مربعنا كما يلي:
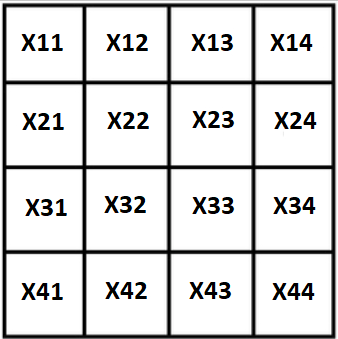
الخاصية الأولى والواضحة: مجموع المربع معروف ، يمكن التعبير عن العوائق المتطرفة من خلال 3 المتبقية:
X14 = S - X11 - X12 - X13
X24 = S - X21 - X22 - X23
...
X41 = S - X11 - X21 - X31وبالتالي ، يتحول مربع 4 × 4 في الواقع إلى مربع 3 × 3 ، مما يقلل من عدد خيارات البحث من 16! ما يصل إلى 9! ، أي 57 مليون مرة. بمعرفة ذلك ، نبدأ في كتابة التعليمات البرمجية ، ونرى مدى تعقيد هذا البحث الشامل لأجهزة الكمبيوتر الحديثة.
C ++ - نسخة واحدة مترابطة
مبدأ البرنامج بسيط جدا. نأخذ مجموعة الأرقام 1..16 وحلقة for فوق هذه المجموعة ، ستكون x11. ثم نأخذ المجموعة الثانية ، التي تتكون من الأولى باستثناء الرقم x11 ، وهكذا.
يبدو الشكل التقريبي للبرنامج كما يلي:
int squares = 0; int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); for (int x11 = 1; x11 <= MAX; x11++) { Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; ... int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue;
يمكن العثور على النص الكامل للبرنامج تحت المفسد.
المصدر بالكامل #include <set> #include <stdio.h> #include <ctime> #include "stdafx.h" typedef std::set<int> Set; typedef Set::iterator SetIterator; #define N 4 #define MAX (N*N) #define S 34 int main(int argc, char *argv[]) { // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 const clock_t begin_time = clock(); int squares = 0; int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); for (int x11 = 1; x11 <= MAX; x11++) { Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; Set set21(set13); set21.erase(x13); set21.erase(x14); for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++) { int x21 = *it21; Set set22(set21); set22.erase(x21); for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++) { int x22 = *it22; Set set23(set22); set23.erase(x22); for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++) { int x23 = *it23, x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; Set set31(set23); set31.erase(x23); set31.erase(x24); for (SetIterator it31 = set31.begin(); it31 != set31.end(); it31++) { int x31 = *it31; Set set32(set31); set32.erase(x31); for (SetIterator it32 = set32.begin(); it32 != set32.end(); it32++) { int x32 = *it32; Set set33(set32); set33.erase(x32); for (SetIterator it33 = set33.begin(); it33 != set33.end(); it33++) { int x33 = *it33, x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x41 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); squares++; } } } } } } } } } printf("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); return 0; }
النتيجة: تم العثور على إجمالي
7040 4x4 "مربعات سحرية" ، وكان وقت البحث
102 ثانية .

بالمناسبة ، من المثير للاهتمام التحقق مما إذا كانت قائمة المربعات تحتوي على نفس المربع المرسوم على نقش Durer. بالطبع هناك ، لأنه يعرض البرنامج
جميع مربعات 4x4:
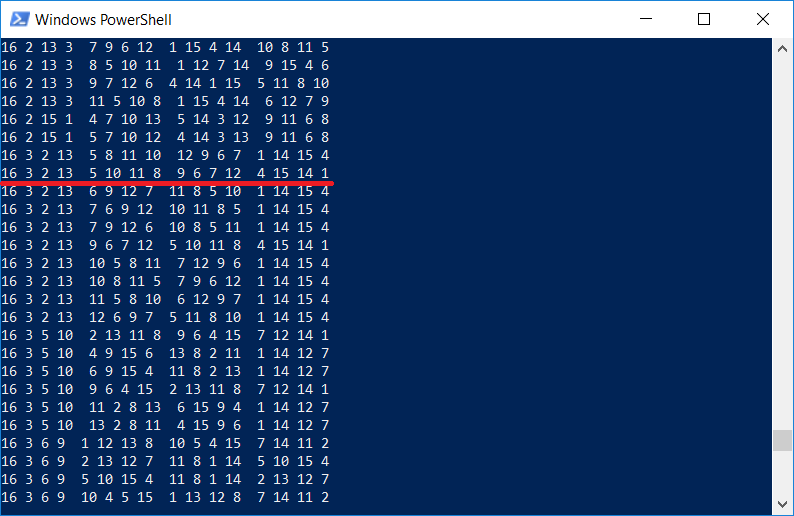
وتجدر الإشارة إلى أن دورر أدخل مربعًا في الصورة لسبب ما ، وتشير الأرقام
1514 أيضًا إلى سنة النقش.
كما ترى ، يعمل البرنامج (نحتفل بالمهمة كما تم التحقق منها في 1514 بواسطة Albrecht Dürer ؛) ، لكن وقت التنفيذ ليس صغيرًا بالنسبة لجهاز كمبيوتر مزود بمعالج Core i7. من الواضح أن البرنامج يعمل في خيط واحد ، ومن المستحسن استخدام جميع النوى الأخرى.
C ++ - نسخة متعددة الخيوط
إعادة كتابة برنامج باستخدام تيارات هو في الأساس بسيط ، وإن كان مرهقًا بعض الشيء. لحسن الحظ ، هناك خيار شبه منسي اليوم - استخدام دعم
OpenMP (Open Multi-Processing). هذه التكنولوجيا موجودة منذ عام 1998 ، وتسمح لتوجيهات المعالج بإخبار المترجم بأجزاء البرنامج التي سيتم تشغيلها بالتوازي. OpenMP مدعوم أيضًا في Visual Studio ، لذلك لتحويل برنامج إلى خيوط متعددة ، ما عليك سوى إضافة سطر واحد إلى الشفرة:
int squares = 0; #pragma omp parallel for reduction(+: squares) for (int x11 = 1; x11 <= MAX; x11++) { ... } printf("CNT: %d\n", squares);
يشير
التوجيه #pragma omp الموازي لـ إلى أنه يمكن تنفيذ الحلقة التالية بالتوازي ، وتعين مربعات المعلمة الإضافية اسم المتغير ، والذي سيكون شائعًا في سلاسل الرسائل المتوازية (بدون هذا ، لا تعمل الزيادة بشكل صحيح).
والنتيجة واضحة: تم تقليل وقت التنفيذ من 102 إلى
18 .

المصدر بالكامل #include <set> #include <stdio.h> #include <ctime> #include "stdafx.h" typedef std::set<int> Set; typedef Set::iterator SetIterator; #define N 4 #define MAX (N*N) #define S 34 int main(int argc, char *argv[]) { // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 const clock_t begin_time = clock(); int squares = 0; #pragma omp parallel for reduction(+: squares) for (int x11 = 1; x11 <= MAX; x11++) { int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; Set set21(set13); set21.erase(x13); set21.erase(x14); for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++) { int x21 = *it21; Set set22(set21); set22.erase(x21); for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++) { int x22 = *it22; Set set23(set22); set23.erase(x22); for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++) { int x23 = *it23, x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; Set set31(set23); set31.erase(x23); set31.erase(x24); for (SetIterator it31 = set31.begin(); it31 != set31.end(); it31++) { int x31 = *it31; Set set32(set31); set32.erase(x31); for (SetIterator it32 = set32.begin(); it32 != set32.end(); it32++) { int x32 = *it32; Set set33(set32); set33.erase(x32); for (SetIterator it33 = set33.begin(); it33 != set33.end(); it33++) { int x33 = *it33, x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x41 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); squares++; } } } } } } } } } printf("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); return 0; }
هذا أفضل بكثير - لأنه تكون المهمة متوازية تمامًا تقريبًا (الحسابات في كل فرع مستقلة عن بعضها البعض) ، والوقت أقل من عدد المرات التي تساوي عدد نوى المعالج. ولكن للأسف ، ليس من الممكن الحصول على المزيد من هذا الرمز ، على الرغم من أن نسبة ضئيلة يمكن تحقيقها من خلال بعض التحسينات. ننتقل إلى المدفعية الثقيلة والحسابات على GPU.
الحوسبة باستخدام NVIDIA CUDA
إذا لم تدخل في التفاصيل ، عندئذٍ يمكن تمثيل عملية الحساب التي يتم إجراؤها على بطاقة الفيديو على أنها عدة كتل أجهزة متوازية (كتل) ، كل منها ينفذ عدة عمليات (سلاسل).
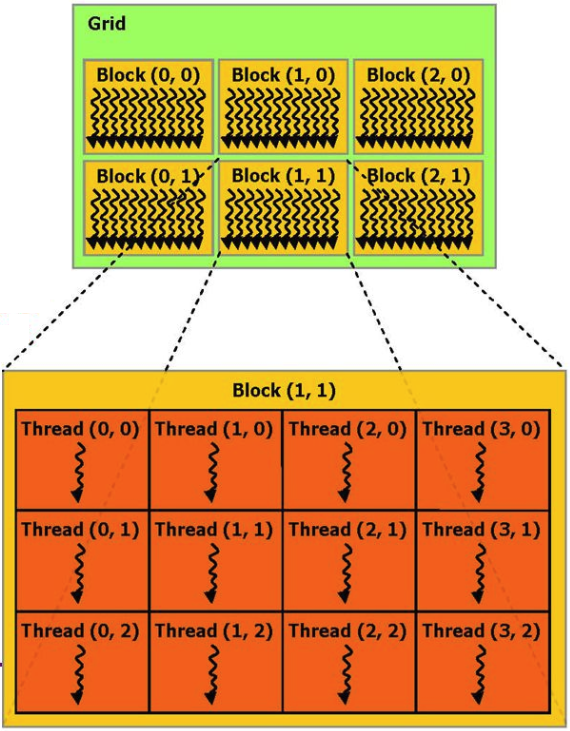
على سبيل المثال ، يمكننا إعطاء مثال على وظيفة إضافة متجهين من وثائق CUDA:
__global__ void add(int n, float *x, float *y) { int index = threadIdx.x; int stride = blockDim.x; for (int i = index; i < n; i += stride) y[i] = x[i] + y[i]; }
تعد المصفوفات x و y شائعة في جميع الكتل ، وبالتالي يتم تنفيذ الوظيفة نفسها في وقت واحد على عدة معالجات في وقت واحد. المفتاح هنا هو التوازي - معالجات بطاقة الفيديو أبسط بكثير من وحدة المعالجة المركزية العادية ، ولكن هناك العديد منها وتركز بشكل خاص على معالجة البيانات الرقمية.
هذا ما نحتاجه. لدينا مصفوفة أرقام X11 ، X12 ، .. ، X44. لنبدأ عملية 16 كتلة ، ستنفذ كل منها 16 عملية. سيتطابق رقم الكتلة مع الرقم X11 ، ورقم العملية مع الرقم X12 ، وسيحسب الرمز نفسه جميع المربعات الممكنة مع X11 و X12 المحددين. الأمر بسيط ، ولكن هناك دقة واحدة - لا تحتاج البيانات فقط إلى حساب ، ولكن أيضًا نقلها من بطاقة الفيديو مرة أخرى ، لذلك سنقوم بتخزين عدد المربعات الموجودة في عنصر الصفر في الصفيف.
الكود الرئيسي بسيط جدا:
#define N 4 #define SQ_MAX 8*1024 #define BLOCK_SIZE (SQ_MAX*N*N + 1) int main(int argc,char *argv[]) { const clock_t begin_time = clock(); int *results = (int*)malloc(BLOCK_SIZE*sizeof(int)); results[0] = 0; int *gpu_out = NULL; cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int)); cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice); squares<<<MAX, MAX>>>(gpu_out); cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost); // Print results int squares = results[0]; for(int p=0; p<SQ_MAX && p<squares; p++) { int i = MAX*p + 1; printf("[%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d]\n", results[i], results[i+1], results[i+2], results[i+3], results[i+4], results[i+5], results[i+6], results[i+7], results[i+8], results[i+9], results[i+10], results[i+11], results[i+12], results[i+13], results[i+14], results[i+15]); } printf ("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); cudaFree(gpu_out); free(results); return 0; }
نختار كتلة الذاكرة على بطاقة الفيديو باستخدام cudaMalloc ، ونقوم بتشغيل وظيفة المربعات ، مع الإشارة إلى معلمتين 16.16 (عدد الكتل وعدد الخيوط) المقابلة للأرقام 1..16 المكررة ، ثم نسخ البيانات مرة أخرى من خلال cudaMemcpy.
تعمل الدالة المربعات نفسها بشكل أساسي على تكرار الرمز من الجزء السابق ، مع اختلاف أن الزيادة في عدد المربعات التي تم العثور عليها باستخدام atomicAdd - وهذا يضمن أن المتغير سيتغير بشكل صحيح أثناء المكالمات المتزامنة.
لا تتطلب النتيجة تعليقات - كان وقت التنفيذ
2.7 ثانية ، وهو أفضل بنحو 30 مرة من النسخة الأولية ذات الخيوط الفردية:

كما هو مقترح في التعليقات ، يمكنك استخدام المزيد من كتل الأجهزة لبطاقة الفيديو ، لذلك تم تجربة خيار 256 كتلة. تغيير الرمز هو الحد الأدنى:
__global__ void squares(int *res_array) { int index1 = blockIdx.x/MAX, index2 = blockIdx.x%MAX; ... } squares<<<MAX*MAX, 1>>>(gpu_out);
أدى هذا إلى تقليل الوقت مرتين
إضافيتين إلى
1.2 ثانية . علاوة على ذلك ، في كل كتلة ، يمكن بدء 16 عملية ، مما يوفر أفضل وقت لـ
0.44 ثانية .
الرمز النهائي #include <stdio.h> #include <ctime> #define N 4 #define MAX (N*N) #define SQ_MAX 8*1024 #define BLOCK_SIZE (SQ_MAX*N*N + 1) #define S 34 // Magic square: // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 __global__ void squares(int *res_array) { int index1 = blockIdx.x/MAX, index2 = blockIdx.x%MAX, index3 = threadIdx.x; if (index1 + 1 > MAX || index2 + 1 > MAX || index3 + 1 > MAX) return; const int x11 = index1+1, x12 = index2+1, x13 = index3+1; if (x13 == x11 || x13 == x12) return; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) return; if (x14 == x11 || x14 == x12 || x14 == x13) return; for(int x21=1; x21<=MAX; x21++) { if (x21 == x11 || x21 == x12 || x21 == x13 || x21 == x14) continue; for(int x22=1; x22<=MAX; x22++) { if (x22 == x11 || x22 == x12 || x22 == x13 || x22 == x14 || x22 == x21) continue; for(int x23=1; x23<=MAX; x23++) { int x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x23 == x11 || x23 == x12 || x23 == x13 || x23 == x14 || x23 == x21 || x23 == x22) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; for(int x31=1; x31<=MAX; x31++) { if (x31 == x11 || x31 == x12 || x31 == x13 || x31 == x14 || x31 == x21 || x31 == x22 || x31 == x23 || x31 == x24) continue; for(int x32=1; x32<=MAX; x32++) { if (x32 == x11 || x32 == x12 || x32 == x13 || x32 == x14 || x32 == x21 || x32 == x22 || x32 == x23 || x32 == x24 || x32 == x31) continue; for(int x33=1; x33<=MAX; x33++) { int x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x33 == x11 || x33 == x12 || x33 == x13 || x33 == x14 || x33 == x21 || x33 == x22 || x33 == x23 || x33 == x24 || x33 == x31 || x33 == x32) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; const int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x44 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; // Square found: save in array (MAX numbers for each square) int p = atomicAdd(res_array, 1); if (p >= SQ_MAX) continue; int i = MAX*p + 1; res_array[i] = x11; res_array[i+1] = x12; res_array[i+2] = x13; res_array[i+3] = x14; res_array[i+4] = x21; res_array[i+5] = x22; res_array[i+6] = x23; res_array[i+7] = x24; res_array[i+8] = x31; res_array[i+9] = x32; res_array[i+10] = x33; res_array[i+11] = x34; res_array[i+12]= x41; res_array[i+13]= x42; res_array[i+14] = x43; res_array[i+15] = x44; // Warning: printf from kernel makes calculation 2-3x slower // printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); } } } } } } } int main(int argc,char *argv[]) { int *gpu_out = NULL; cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int)); const clock_t begin_time = clock(); int *results = (int*)malloc(BLOCK_SIZE*sizeof(int)); results[0] = 0; cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice); squares<<<MAX*MAX, MAX>>>(gpu_out); cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost); // Print results int squares = results[0]; for(int p=0; p<SQ_MAX && p<squares; p++) { int i = MAX*p + 1; printf("[%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d]\n", results[i], results[i+1], results[i+2], results[i+3], results[i+4], results[i+5], results[i+6], results[i+7], results[i+8], results[i+9], results[i+10], results[i+11], results[i+12], results[i+13], results[i+14], results[i+15]); } printf ("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); cudaFree(gpu_out); free(results); return 0; }
على الأرجح ، هذا أبعد ما يكون عن المثالية ، على سبيل المثال ، يمكنك تشغيل المزيد من الكتل على وحدة معالجة الرسومات ، ولكن هذا سيجعل الرمز أكثر إرباكًا ويصعب فهمه. وبالطبع ، فإن الحسابات ليست "مجانية" - عندما يتم تحميل GPU ، تبدأ واجهة Windows في الإبطاء بشكل ملحوظ ، ويزداد استهلاك طاقة الكمبيوتر مرتين تقريبًا ، من 65 إلى 130 وات.
تعديل : كما اقترح مستخدم
Bodigrim في التعليقات ، هناك مساواة أخرى
تملأ مربع 4x4: مجموع 4 خلايا "داخلية" يساوي مجموع الخلايا "الخارجية" ، وهو أيضًا S.

X22 + X23 + X32 + X33 = X11 + X41 + X14 + X44 = Sهذا سيجعل من الممكن تسريع الخوارزمية عن طريق التعبير عن بعض المتغيرات من خلال الآخرين وإزالة حلقات أخرى متداخلة 1-2 ؛ يمكن العثور على نسخة محدثة من التعليمات البرمجية في التعليق أدناه.الخلاصة
وتبين أن مهمة إيجاد "الساحات السحرية" كانت مهمة من الناحية الفنية ، وصعبة في نفس الوقت. حتى مع الحسابات على GPU ، يمكن أن يستغرق البحث عن جميع المربعات 5x5 عدة ساعات ، ولا يزال التحسين للعثور على المربعات السحرية 7x7 وأبعاد أعلى لا يزال يتعين القيام به.من الناحية الرياضية والخوارزمية ، هناك أيضًا العديد من المشكلات التي لم يتم حلها:- « » N. 22 , 33 8 ( 1, ), 44 , 7040, . .
- , .
- . , NVIDIA Tesla , - , . , . , ;)
يمكن كتابة مقال منفصل عن تحليل وخصائص المربعات السحرية نفسها ، إذا كان هناك اهتمام.ملاحظة: بالنسبة للسؤال الذي من المحتمل أن يتبع ، "لماذا هذا ضروري". من حيث استهلاك الطاقة ، فإن حساب المربعات السحرية ليس أفضل أو أسوأ من حساب البيتكوين ، فلماذا لا؟ بالإضافة إلى ذلك ، فهو تمرين مثير للاهتمام للعقل ومهمة مثيرة للاهتمام في مجال البرمجة التطبيقية.