نحن نقوم بمشروع تعلُّم الآلة في Python. الجزء الأول

ترجمة مشروع كامل للتعلم الآلي في بايثون: الجزء الأول .

عندما تقرأ كتابًا أو تستمع إلى دورة تدريبية حول تحليل البيانات ، غالبًا ما تشعر بأنك تواجه بعض أجزاء منفصلة من الصورة التي لا يمكن تجميعها معًا. قد تشعر بالخوف من احتمال اتخاذ الخطوة التالية وحل مشكلة ما بالكامل باستخدام التعلم الآلي ، ولكن بمساعدة هذه السلسلة من المقالات ستكتسب الثقة في القدرة على حل أي مشكلة في مجال علم البيانات.

لكي تحصل على صورة كاملة في ذهنك أخيرًا ، نقترح التحليل من البداية إلى النهاية لمشروع استخدام التعلم الآلي باستخدام بيانات حقيقية.

اتبع الخطوات المتتالية:

1. تنظيف وتنسيق البيانات.
2. تحليل البيانات الاستكشافية.
3. تصميم واختيار الميزات.
4. مقارنة مقاييس العديد من نماذج التعلم الآلي.
5. ضبط أفضل من المعلمات.
6. تقييم أفضل نموذج في مجموعة بيانات الاختبار.
7. تفسير نتائج النموذج.
8. الاستنتاجات والعمل مع الوثائق.

سوف تتعلم كيف تنتقل المراحل إلى أخرى وكيفية تنفيذها في Python. المشروع بأكمله متاح على جيثب ، الجزء الأول يكمن هنا. في هذه المقالة سننظر في المراحل الثلاث الأولى.

وصف المهمة

قبل كتابة التعليمات البرمجية ، تحتاج إلى فهم المشكلة التي يتم حلها والبيانات المتاحة. في هذا المشروع ، سنعمل مع بيانات كفاءة الطاقة المتاحة للجمهور للمباني في نيويورك.

هدفنا: استخدام البيانات المتاحة لبناء نموذج يتنبأ بعدد Energy Star Score لمبنى معين ، وتفسير النتائج للعثور على العوامل التي تؤثر على النتيجة النهائية.

تتضمن البيانات بالفعل نقاط Energy Star المعينة ، لذا فإن مهمتنا هي التعلم الآلي من خلال الانحدار المتحكم فيه:

• خاضع للإشراف: نحن نعلم العلامات والغرض ، ومهمتنا هي تدريب نموذج يمكن أن يقارن الأول بالنموذج الثاني.
• الانحدار: إن Energy Star Score هو متغير مستمر.

يجب أن يكون نموذجنا دقيقًا - حتى يتمكن من توقع قيمة نقاط Energy Star قريبة من الحقيقة - وقابلة للتفسير - حتى نتمكن من فهم توقعاته. بمعرفة البيانات المستهدفة ، يمكننا استخدامها عند اتخاذ القرارات عندما نتعمق في البيانات وننشئ النموذج.

تطهير البيانات

ليست كل مجموعة بيانات هي مجموعة متطابقة تمامًا من الملاحظات ، بدون حالات شاذة وقيم مفقودة (تلميح إلى مجموعات بيانات mtcars وقزحية العين ). في البيانات الحقيقية ، هناك القليل من النظام ، لذلك قبل أن تبدأ التحليل ، تحتاج إلى مسحه وتقديمه إلى تنسيق مقبول. يعد تنظيف البيانات إجراءً غير سار ولكنه إلزامي في حل معظم مهام تحليل البيانات.

أولاً ، يمكنك تحميل البيانات في شكل Patas dataframe وفحصها:

import pandas as pd import numpy as np # Read in data into a dataframe data = pd.read_csv('data/Energy_and_Water_Data_Disclosure_for_Local_Law_84_2017__Data_for_Calendar_Year_2016_.csv') # Display top of dataframe data.head() 

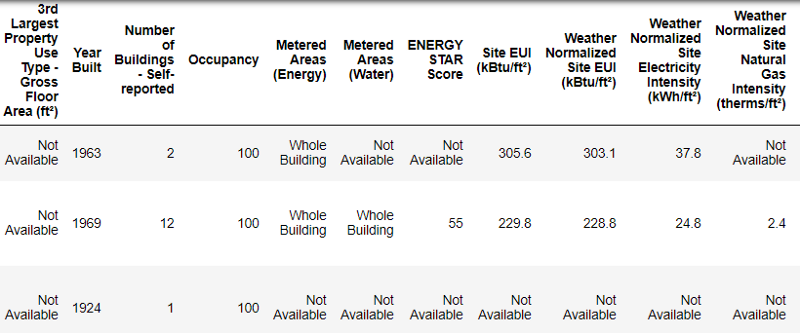هكذا تبدو البيانات الحقيقية.

هذا جزء من جدول مكون من 60 عمودًا. حتى هنا ، تظهر العديد من المشاكل: نحن بحاجة إلى توقع نتيجة Energy Star Score ، لكننا لا نعرف ماذا تعني كل هذه الأعمدة. على الرغم من أن هذه ليست مشكلة بالضرورة ، لأنه يمكنك غالبًا إنشاء نموذج دقيق دون معرفة أي شيء عن المتغيرات على الإطلاق. لكن قابلية التفسير مهمة بالنسبة لنا ، لذلك نحتاج إلى معرفة معنى بعض الأعمدة على الأقل.

عندما تلقينا هذه البيانات ، لم نسأل عن القيم ، ولكن نظرنا إلى اسم الملف:



وقررت البحث عن "القانون المحلي 84". وجدنا هذه الصفحة ، التي تقول أننا نتحدث عن القانون المعمول به في نيويورك ، والذي بموجبه يجب على مالكي جميع المباني ذات الحجم المحدد الإبلاغ عن استهلاك الطاقة. ساعد البحث الإضافي في العثور على جميع قيم الأعمدة . لذلك لا تهمل أسماء الملفات ، فقد تكون نقطة بداية جيدة. بالإضافة إلى ذلك ، هذا تذكير بأنك لا تتسرع ولا تفوت شيئًا مهمًا!

لن ندرس جميع الأعمدة ، لكننا بالتأكيد سنتعامل مع برنامج Energy Star Score ، الموصوف على النحو التالي:

الترتيب المئوي من 1 إلى 100 ، والذي يتم حسابه على أساس التقارير السنوية حول استهلاك الطاقة من قبل أصحاب المباني أنفسهم. مقياس Energy Star هو مقياس نسبي يستخدم لمقارنة أداء الطاقة في المباني.

تم حل المشكلة الأولى ، ولكن بقيت الثانية - قيم مفقودة ، تم وضع علامة "غير متوفر". هذه قيمة سلسلة في Python ، مما يعني أنه حتى السلاسل بالأرقام سيتم تخزينها على أنها أنواع بيانات object ، لأنه إذا كان هناك أي سلسلة في العمود ، فإن Pandas تحولها إلى عمود يتكون بالكامل من سلسلة. يمكن العثور على أنواع بيانات العمود باستخدام طريقة dataframe.info() :

 # See the column data types and non-missing values data.info() 

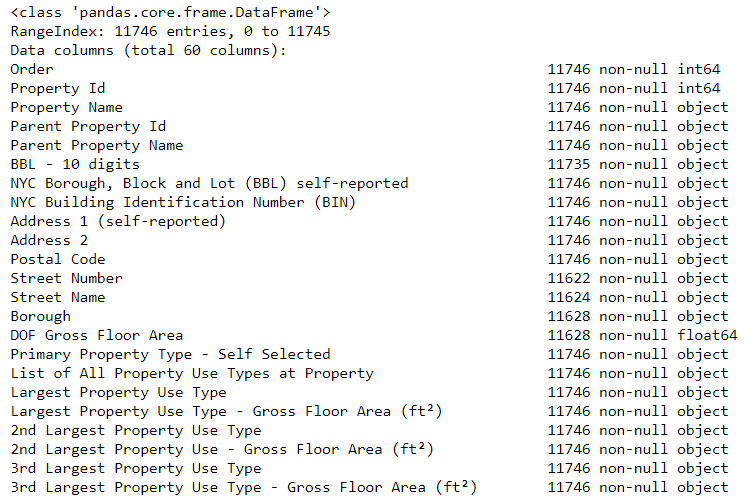
بالتأكيد يتم تخزين بعض الأعمدة التي تحتوي على أرقام بشكل صريح (مثل ft²) ككائنات. لا يمكننا تطبيق التحليل العددي على قيم السلاسل ، لذلك نقوم بتحويلها إلى أنواع البيانات العددية (خاصة float )!

يستبدل هذا الرمز أولاً جميع "غير متوفر" برقم ( np.nan ) ، والذي يمكن تفسيره كأرقام ، ثم يحول محتويات أعمدة معينة إلى نوع float :

 # Replace all occurrences of Not Available with numpy not a number data = data.replace({'Not Available': np.nan}) # Iterate through the columns for col in list(data.columns): # Select columns that should be numeric if ('ft²' in col or 'kBtu' in col or 'Metric Tons CO2e' in col or 'kWh' in col or 'therms' in col or 'gal' in col or 'Score' in col): # Convert the data type to float data[col] = data[col].astype(float) 

عندما تصبح القيم في الأعمدة المقابلة معنا أرقامًا ، يمكننا البدء في فحص البيانات.

بيانات مفقودة وغير طبيعية

إلى جانب أنواع البيانات غير الصحيحة ، فإن إحدى المشاكل الأكثر شيوعًا هي نقص القيم. قد تكون غائبة لأسباب مختلفة ، وقبل تدريب النموذج ، يجب إما ملء هذه القيم أو حذفها. أولاً ، دعنا نكتشف عدد القيم التي لدينا في كل عمود ( الكود موجود هنا ).


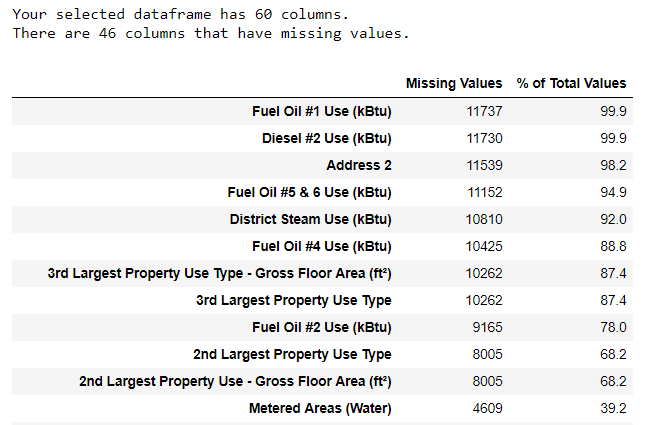لإنشاء جدول ، تم استخدام وظيفة من فرع على StackOverflow .

يجب دائمًا إزالة المعلومات بحذر ، وإذا كانت هناك قيم كثيرة في العمود ، فمن المحتمل ألا تفيد نموذجنا. يعتمد الحد الأدنى الذي من الأفضل بعده التخلص من الأعمدة على مهمتك ( هنا مناقشة ) ، وفي مشروعنا سنحذف الأعمدة التي تكون أكثر من نصف فارغة.

أيضًا في هذه المرحلة ، من الأفضل إزالة القيم غير الطبيعية. يمكن أن تحدث بسبب الأخطاء المطبعية عند إدخال البيانات أو بسبب أخطاء في وحدات القياس ، أو يمكن أن تكون صحيحة ، ولكن القيم المتطرفة. في هذه الحالة ، سنزيل القيم "الإضافية" ، مسترشدةً بتعريف الحالات الشاذة المتطرفة :

• أسفل الربع الأول يوجد نطاق 3∗ رباعي.
• فوق الربع الثالث + 3 range المدى الربيعي.

يتم سرد التعليمات البرمجية التي تزيل الأعمدة والشذوذ في "المفكرة" على Github. عند الانتهاء من عملية تطهير البيانات وإزالة الشذوذ ، لدينا أكثر من 11000 مبنى و 49 علامة.

تحليل البيانات الاستكشافية

تم الانتهاء من المرحلة المملة ، ولكن الضرورية لتنظيف البيانات ، يمكنك الذهاب إلى الدراسة! تحليل البيانات الاستكشافية (RAD) هو عملية زمنية غير محدودة نقوم خلالها بحساب الإحصائيات والبحث عن الاتجاهات أو الشذوذ أو الأنماط أو العلاقات في البيانات.

باختصار ، RAD هي محاولة لمعرفة البيانات التي يمكن أن تخبرنا. عادة ، يبدأ التحليل بمراجعة سطحية ، ثم نجد أجزاء مثيرة للاهتمام ونحللها بمزيد من التفصيل. قد تكون النتائج مثيرة للاهتمام في حد ذاتها ، أو قد تساهم في اختيار النموذج ، مما يساعد على تحديد الميزات التي سنستخدمها.

الرسوم البيانية أحادية المتغير

هدفنا هو توقع قيمة Energy Star Score (تمت إعادة تسميتها إلى score في بياناتنا) ، لذلك من المنطقي أن تبدأ بفحص توزيع هذا المتغير. الرسم البياني هو طريقة بسيطة ولكنها فعالة لتصور توزيع متغير واحد ، ويمكن بناؤه بسهولة باستخدام matplotlib .

 import matplotlib.pyplot as plt # Histogram of the Energy Star Score plt.style.use('fivethirtyeight') plt.hist(data['score'].dropna(), bins = 100, edgecolor = 'k'); plt.xlabel('Score'); plt.ylabel('Number of Buildings'); plt.title('Energy Star Score Distribution'); 

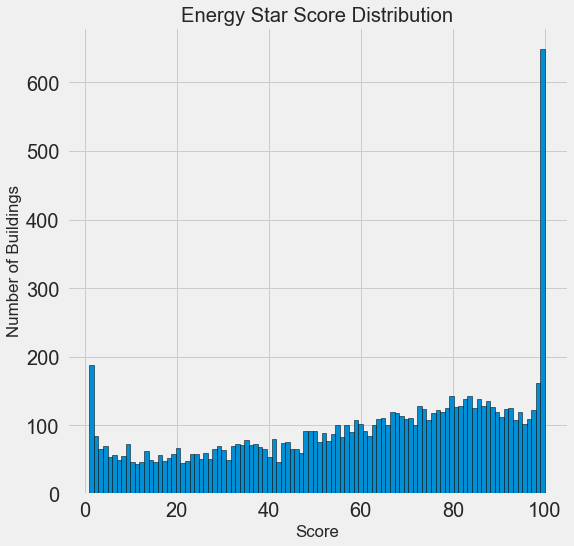
تبدو مشبوهة! نقاط Energy Star هي نسبة مئوية ، لذلك يجب أن تتوقع توزيعًا موحدًا عندما يتم تعيين كل نقطة على نفس عدد المباني. ومع ذلك ، حصل عدد كبير من المباني بشكل غير متناسب على أعلى وأدنى نتائج (بالنسبة لنجم إنرجي ستار ، كلما كان ذلك أفضل).

إذا نظرنا مرة أخرى إلى تعريف هذه النتيجة ، فسوف نرى أنه يتم حسابها على أساس "التقارير التي يتم ملؤها بشكل مستقل من قبل أصحاب المباني" ، والتي قد تفسر زيادة القيم الكبيرة جدًا. إن مطالبة أصحاب المباني بالإبلاغ عن استهلاكهم للطاقة يشبه مطالبة الطلاب بالإبلاغ عن درجاتهم في الاختبارات. لذلك ربما لا يكون هذا هو المعيار الأكثر موضوعية لتقييم كفاءة الطاقة في العقارات.

إذا كان لدينا وقت غير محدود من الوقت ، فيمكننا معرفة سبب حصول العديد من المباني على نقاط عالية جدًا ومنخفضة جدًا. للقيام بذلك ، سيكون علينا اختيار المباني المناسبة وتحليلها بعناية. ولكننا نحتاج فقط إلى تعلم كيفية التنبؤ بالدرجات ، وليس تطوير طريقة تقييم أكثر دقة. يمكنك تمييز نفسك بأن النقاط لها توزيع مشبوه ، لكننا سنركز على التنبؤ.

البحث عن العلاقات

الجزء الرئيسي من AHFR هو البحث عن العلاقة بين العلامات وهدفنا. المتغيرات المرتبطة به مفيدة للاستخدام في النموذج ، لأنه يمكن استخدامها للتنبؤ. تتمثل إحدى طرق دراسة تأثير المتغير الفصلي (الذي لا يأخذ سوى مجموعة محدودة من القيم) على الهدف في رسم الكثافة باستخدام مكتبة Seaborn.

يمكن اعتبار الرسم البياني للكثافة رسمًا بيانيًا سلسًا لأنه يوضح توزيع متغير واحد. يمكنك تلوين الفئات الفردية على الرسم البياني لترى كيف يغير المتغير الفصلي التوزيع. يرسم هذا الرمز مخطط كثافة Energy Star Score ، الملون وفقًا لنوع المبنى (للحصول على قائمة بالمباني ذات أكثر من 100 أبعاد):

 # Create a list of buildings with more than 100 measurements types = data.dropna(subset=['score']) types = types['Largest Property Use Type'].value_counts() types = list(types[types.values > 100].index) # Plot of distribution of scores for building categories figsize(12, 10) # Plot each building for b_type in types: # Select the building type subset = data[data['Largest Property Use Type'] == b_type] # Density plot of Energy Star Scores sns.kdeplot(subset['score'].dropna(), label = b_type, shade = False, alpha = 0.8); # label the plot plt.xlabel('Energy Star Score', size = 20); plt.ylabel('Density', size = 20); plt.title('Density Plot of Energy Star Scores by Building Type', size = 28); 

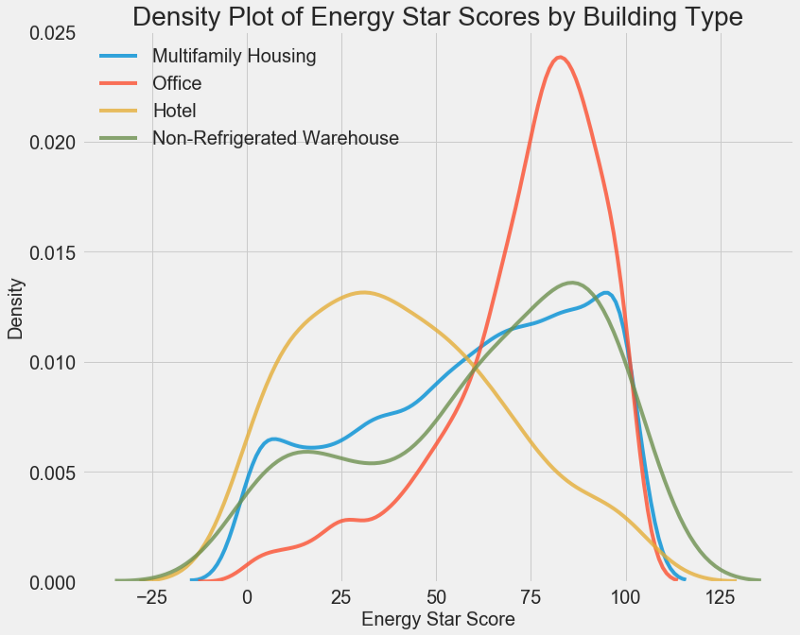
كما ترى ، يؤثر نوع المبنى بشكل كبير على عدد النقاط. عادةً ما تحصل مباني المكاتب على درجات أعلى وفنادق أقل. لذلك تحتاج إلى تضمين نوع المبنى في النموذج ، لأن هذه العلامة تؤثر على هدفنا. كمتغير فئوي ، يجب علينا إجراء ترميز واحد لنوع المبنى.

يمكن استخدام رسم بياني مشابه لتقدير نقاط إنرجي ستار حسب منطقة المدينة:



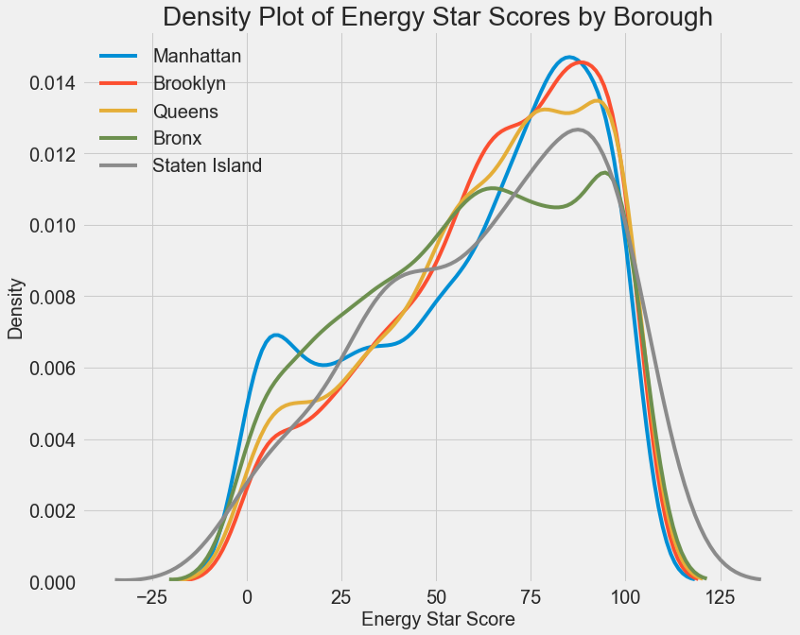
لا تؤثر المنطقة على الدرجة بقدر نوع المبنى. ومع ذلك ، سنقوم بإدراجه في النموذج ، لأنه يوجد فرق طفيف بين المناطق.

لحساب العلاقة بين المتغيرات ، يمكنك استخدام معامل ارتباط بيرسون . هذا مقياس لشدة واتجاه العلاقة الخطية بين متغيرين. تعني قيمة +1 علاقة إيجابية خطية تمامًا ، وتعني -1 علاقة سلبية خطية تمامًا. فيما يلي بعض الأمثلة لقيم معامل ارتباط بيرسون :



على الرغم من أن هذا المعامل لا يمكن أن يعكس التبعيات غير الخطية ، فمن الممكن أن تبدأ به لتقييم علاقات المتغيرات. في Pandas ، يمكنك بسهولة حساب الارتباطات بين أي أعمدة في إطار البيانات:

 # Find all correlations with the score and sort correlations_data = data.corr()['score'].sort_values() 

الارتباطات الأكثر سلبية مع الهدف:



والأكثر إيجابية:



هناك العديد من الارتباطات السلبية القوية بين السمات والهدف ، وأكبرها ينتمي إلى فئات مختلفة من EUI (تختلف طرق حساب هذه المؤشرات قليلاً). EUI (كثافة استخدام الطاقة ) هي كمية الطاقة المستهلكة في مبنى مقسومة على قدم مربع من المساحة. يتم استخدام هذه القيمة المحددة لتقييم كفاءة الطاقة ، وكلما كانت أصغر ، كان ذلك أفضل. يقترح المنطق أن هذه الارتباطات لها ما يبررها: إذا زاد مؤشر الاتحاد الأوروبي ، فيجب أن تنخفض نقاط إنرجي ستار.

الرسوم البيانية المتغيرة

نستخدم مؤامرات مبعثرة لتصور العلاقات بين متغيرين متواصلين. يمكنك إضافة معلومات إضافية إلى ألوان النقاط ، على سبيل المثال ، متغير فئوي. العلاقة بين نقاط Energy Star و EUI موضحة أدناه ، تشير الألوان إلى أنواع مختلفة من المباني:



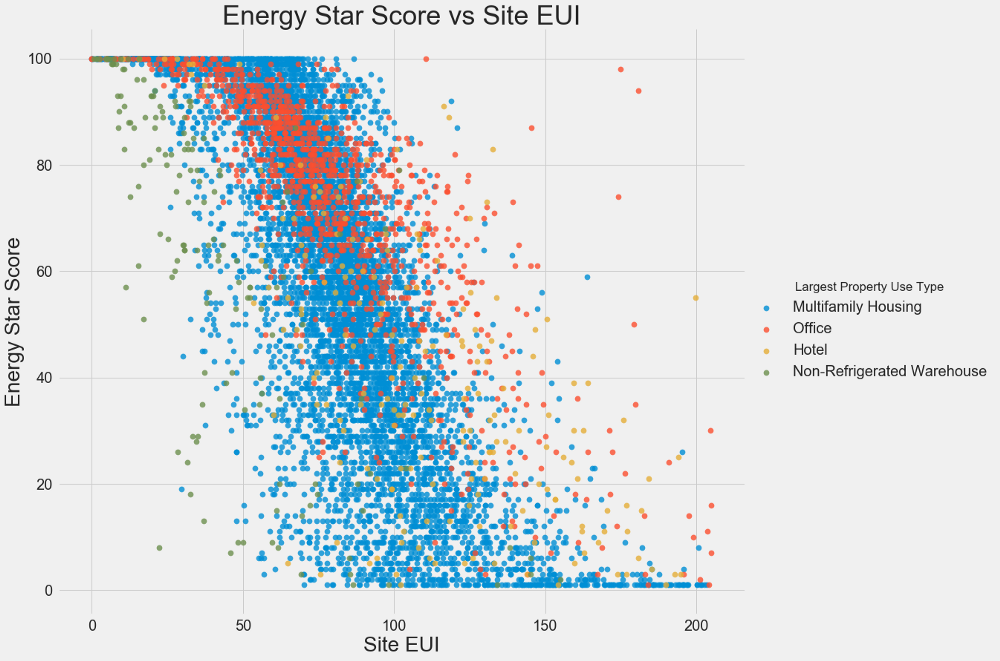
يتيح لك هذا الرسم البياني تصور معامل الارتباط -0.7. مع انخفاض EUI ، تزداد نقاط Energy Star ، وتلاحظ هذه العلاقة في أنواع مختلفة من المباني.

يسمى مخطط البحث الأخير لدينا مؤامرة أزواج . هذه أداة رائعة لمعرفة العلاقات بين الأزواج المختلفة للمتغيرات وتوزيع المتغيرات الفردية. سوف نستخدم مكتبة Seaborn ووظيفة PairGrid لإنشاء مخطط زوجي مع مخطط مبعثر في المثلث العلوي ، مع رسم بياني قطري ، ومخطط كثافة نواة ثنائي الأبعاد ومعاملات الارتباط في المثلث السفلي.

 # Extract the columns to plot plot_data = features[['score', 'Site EUI (kBtu/ft²)', 'Weather Normalized Source EUI (kBtu/ft²)', 'log_Total GHG Emissions (Metric Tons CO2e)']] # Replace the inf with nan plot_data = plot_data.replace({np.inf: np.nan, -np.inf: np.nan}) # Rename columns plot_data = plot_data.rename(columns = {'Site EUI (kBtu/ft²)': 'Site EUI', 'Weather Normalized Source EUI (kBtu/ft²)': 'Weather Norm EUI', 'log_Total GHG Emissions (Metric Tons CO2e)': 'log GHG Emissions'}) # Drop na values plot_data = plot_data.dropna() # Function to calculate correlation coefficient between two columns def corr_func(x, y, **kwargs): r = np.corrcoef(x, y)[0][1] ax = plt.gca() ax.annotate("r = {:.2f}".format(r), xy=(.2, .8), xycoords=ax.transAxes, size = 20) # Create the pairgrid object grid = sns.PairGrid(data = plot_data, size = 3) # Upper is a scatter plot grid.map_upper(plt.scatter, color = 'red', alpha = 0.6) # Diagonal is a histogram grid.map_diag(plt.hist, color = 'red', edgecolor = 'black') # Bottom is correlation and density plot grid.map_lower(corr_func); grid.map_lower(sns.kdeplot, cmap = plt.cm.Reds) # Title for entire plot plt.suptitle('Pairs Plot of Energy Data', size = 36, y = 1.02); 

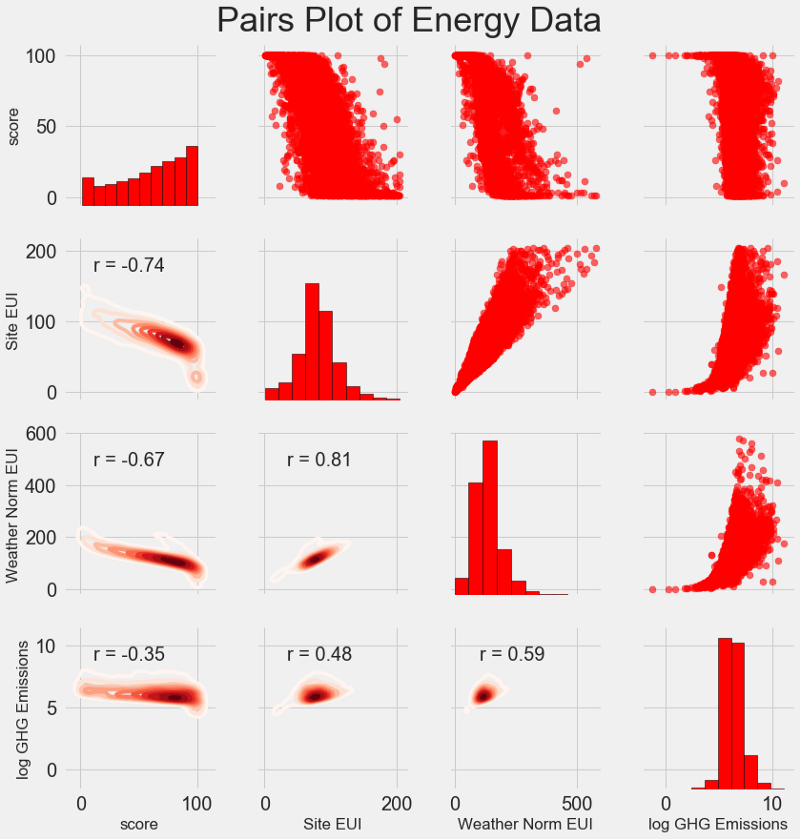
لمعرفة علاقة المتغيرات ، ابحث عن تقاطع الصفوف والأعمدة. افترض أنك تريد إلقاء نظرة على العلاقة بين Weather Norm EUI score ، ثم نبحث عن سلسلة Weather Norm EUI وعمود score ، عند التقاطع الذي يوجد فيه معامل الارتباط -0.67. لا تبدو هذه الرسوم البيانية رائعة فحسب ، بل تساعد أيضًا في اختيار المتغيرات للنموذج.

تصميم واختيار الميزات

غالبًا ما يجلب تصميم الميزات واختيارها أكبر عائد من حيث الوقت الذي يقضيه في تعلم الآلة. أولا نعطي التعاريف:

• البناء المميز : عملية استخراج أو إنشاء خصائص جديدة من البيانات الخام. لاستخدام المتغيرات في النموذج ، قد تحتاج إلى تحويلها ، على سبيل المثال ، أخذ اللوغاريتم الطبيعي ، أو استخراج الجذر التربيعي ، أو تطبيق ترميز واحد ساخن للمتغيرات الفئوية. يمكن اعتبار التصميم المميز على أنه إنشاء ميزات إضافية من البيانات الأولية.
• اختيار الميزة: عملية اختيار الميزات الأكثر صلة من البيانات ، والتي نزيل خلالها بعض الميزات لمساعدة النموذج على تعميم البيانات الجديدة بشكل أفضل من أجل الحصول على نموذج أكثر قابلية للتفسير. يمكن اعتبار اختيار العلامات بمثابة إزالة "زائدة عن الحاجة" بحيث يبقى فقط أهمها.

يمكن أن يتعلم نموذج التعلم الآلي فقط من البيانات التي نقدمها ، لذا من المهم للغاية التأكد من تضمين جميع المعلومات ذات الصلة بمهمتنا. إذا لم تقم بتزويد النموذج بالبيانات الصحيحة ، فلن يكون قادرًا على التعلم ولن ينتج توقعات دقيقة!

سنفعل ما يلي:

• ينطبق على المتغيرات الفئوية (ربع ونوع الملكية) تشفير واحد.
• أضف اللوغاريتم الطبيعي لجميع المتغيرات العددية.

يعد الترميز أحاديًا ضروريًا من أجل تضمين المتغيرات الفئوية في النموذج. لن تتمكن خوارزمية التعلم الآلي من فهم نوع "المكتب" ، لذلك إذا كان المبنى عبارة عن مكتب ، فسنعينه علامة 1 ، وإذا لم يكن مكتبًا ، فعندئذٍ 0.

ستساعد إضافة ميزات محولة النموذج على التعرف على العلاقات غير الخطية داخل البيانات. في تحليل البيانات ، من المعتاد استخراج الجذور التربيعية ، أو أخذ اللوغاريتمات الطبيعية أو تحويل العلامات بطريقة أو بأخرى ، الأمر يعتمد على المهمة المحددة أو معرفتك بأفضل التقنيات. في هذه الحالة ، سنضيف اللوغاريتم الطبيعي لجميع العلامات العددية.

يختار هذا الرمز العلامات العددية ، ويحسب اللوغاريتمات الخاصة بها ، ويحدد علامتي فئتين ، ويطبق عليها ترميزًا ساخنًا واحدًا ، ويجمع كلا المجموعتين في واحدة. إذا حكمنا من خلال الوصف ، لا يزال هناك الكثير من العمل الذي يتعين القيام به ، ولكن في Pandas كل شيء بسيط للغاية!

 # Copy the original data features = data.copy() # Select the numeric columns numeric_subset = data.select_dtypes('number') # Create columns with log of numeric columns for col in numeric_subset.columns: # Skip the Energy Star Score column if col == 'score': next else: numeric_subset['log_' + col] = np.log(numeric_subset[col]) # Select the categorical columns categorical_subset = data[['Borough', 'Largest Property Use Type']] # One hot encode categorical_subset = pd.get_dummies(categorical_subset) # Join the two dataframes using concat # Make sure to use axis = 1 to perform a column bind features = pd.concat([numeric_subset, categorical_subset], axis = 1) 

لدينا الآن أكثر من 11000 ملاحظة (مباني) مع 110 أعمدة (علامات). لن تكون جميع العلامات مفيدة للتنبؤ بنجم إنرجي ستار ، لذلك سنتناول اختيار العلامات وإزالة بعض المتغيرات.

اختيار الميزة

العديد من العلامات الـ 110 المتاحة زائدة عن الحاجة لأنها ترتبط ببعضها البعض بقوة. على سبيل المثال ، هنا رسم بياني لـ EUI و Weather Normalized Site EUI ، مع معامل ارتباط قدره 0.997.



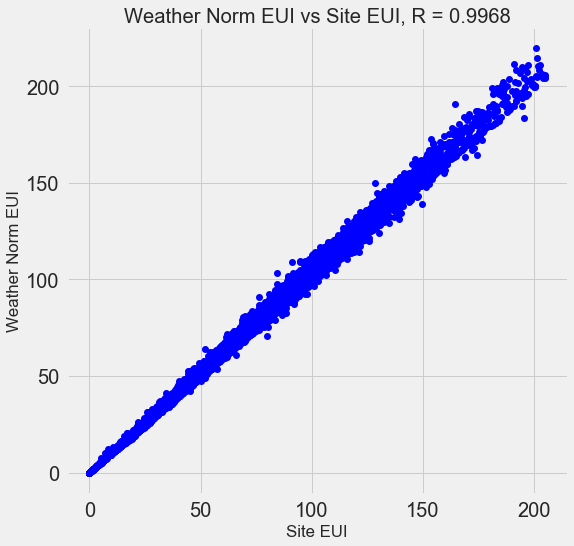
تسمى العلامات التي ترتبط بقوة مع بعضها البعض علاقة خطية متداخلة . غالبًا ما تساعد إزالة متغير واحد في هذه الأزواج من السمات النموذج على التعميم ويكون أكثر قابلية للتفسير . يرجى ملاحظة أننا نتحدث عن ارتباط بعض العلامات مع الآخرين ، وليس عن الارتباط بالهدف ، مما سيساعد نموذجنا فقط!

هناك عدد من الطرق لحساب العلاقة الخطية المتداخلة للميزات ، وأكثرها شيوعًا هو عامل تضخم التباين . سنستخدم معامل bcorrelation للبحث وإزالة الميزات المتداخلة. نتجاهل زوجًا واحدًا من الإشارات إذا كان معامل الارتباط بينهما أكبر من 0.6. الرمز موجود في المفكرة (واستجابة لـ Stack Overflow ).

تبدو هذه القيمة تعسفية ، لكني في الواقع جربت عتبات مختلفة ، وقد سمح لي أعلاه بإنشاء أفضل نموذج. إن التعلم الآلي أمر تجريبي ، وغالبًا ما يتعين عليه التجربة لإيجاد أفضل حل. بعد الاختيار ، لدينا 64 سمة وهدف واحد.

 # Remove any columns with all na values features = features.dropna(axis=1, how = 'all') print(features.shape) (11319, 65) 

اختر مستوى أساسي

قمنا بمسح البيانات ، وإجراء تحليل استكشافي ، وبناء العلامات. وقبل الشروع في إنشاء النموذج ، تحتاج إلى تحديد المستوى الأساسي الأولي (خط الأساس الساذج) - وهو نوع من الافتراض الذي سنقارن به نتائج النماذج. إذا كانت أقل من المستوى الأساسي ، فسوف نفترض أن التعلم الآلي لا ينطبق على هذه المهمة ، أو أنه يجب تجربة نهج مختلف.

بالنسبة لمهام الانحدار ، كمستوى أساسي ، من المعقول تخمين القيمة المتوسطة للهدف في مجموعة التدريب لجميع الأمثلة في مجموعة الاختبار. تضع هذه المجموعات حاجزًا منخفضًا نسبيًا لأي طراز.

كمقياس ، نأخذ متوسط ​​الخطأ المطلق (mae) في التوقعات. هناك العديد من المقاييس الأخرى للانحدارات ، لكني أحب النصيحة لاختيار مقياس واحد واستخدامه لتقييم النماذج. ومتوسط ​​الخطأ المطلق سهل الحساب والتفسير.

قبل حساب المستوى الأساسي ، تحتاج إلى تقسيم البيانات إلى مجموعات تدريب واختبار:

1. مجموعة من السمات التدريبية هي ما نقدمه نموذجنا مع الإجابات أثناء التدريب. يجب أن يتعلم النموذج لتتناسب مع خصائص الهدف.
2. يتم استخدام مجموعة ميزات الاختبار لتقييم النموذج المدرب. عندما تعالج مجموعة الاختبار ، فإنها لا ترى الإجابات الصحيحة ويجب عليها التنبؤ بناءً على الميزات المتاحة فقط. نحن نعرف إجابات بيانات الاختبار ويمكننا مقارنة نتائج التنبؤ بها.

للتدريب ، نستخدم 70٪ من البيانات ، وللاختبار - 30٪:

 # Split into 70% training and 30% testing set X, X_test, y, y_test = train_test_split(features, targets, test_size = 0.3, random_state = 42) 

الآن نقوم بحساب المؤشر لمستوى الأساس الأولي:

 # Function to calculate mean absolute error def mae(y_true, y_pred): return np.mean(abs(y_true - y_pred)) baseline_guess = np.median(y) print('The baseline guess is a score of %0.2f' % baseline_guess) print("Baseline Performance on the test set: MAE = %0.4f" % mae(y_test, baseline_guess)) 

تخمين خط الأساس هو درجة 66.00
أداء خط الأساس في مجموعة الاختبار: MAE = 24.5164

كان متوسط ​​الخطأ المطلق في مجموعة الاختبار حوالي 25 نقطة. نظرًا لأننا نقيم في النطاق من 1 إلى 100 ، فإن الخطأ هو 25 ٪ - وهو حاجز منخفض إلى حد ما للنموذج!

الخلاصة

في هذا المقال ، مررنا بالمراحل الثلاث الأولى لحل مشكلة باستخدام التعلم الآلي. بعد تحديد المهمة ، نقوم بما يلي:

1. مسح البيانات الأولية وتنسيقها.
2. أجرى التحليل الاستكشافي لدراسة البيانات المتاحة.
3. قمنا بتطوير مجموعة من الميزات التي سنستخدمها لنماذجنا.

, , .

Scikit-Learn , .