معهد ماساتشوستس للتكنولوجيا. محاضرة رقم 6.858. "أمن أنظمة الكمبيوتر." نيكولاي زيلدوفيتش ، جيمس ميكنز. 2014 سنة
أمان أنظمة الكمبيوتر هي دورة حول تطوير وتنفيذ أنظمة الكمبيوتر الآمنة. تغطي المحاضرات نماذج التهديد ، والهجمات التي تهدد الأمن ، وتقنيات الأمان بناءً على العمل العلمي الحديث. تشمل الموضوعات أمان نظام التشغيل (OS) ، والميزات ، وإدارة تدفق المعلومات ، وأمان اللغة ، وبروتوكولات الشبكة ، وأمان الأجهزة ، وأمان تطبيقات الويب.
المحاضرة 1: "مقدمة: نماذج التهديد"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 2: "السيطرة على هجمات القراصنة"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 3: "تجاوزات العازلة: المآثر والحماية"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 4: "فصل الامتيازات"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 5: "من أين تأتي أنظمة الأمن؟"
الجزء 1 /
الجزء 2المحاضرة 6: "الفرص"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 7: "وضع حماية العميل الأصلي"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 8: "نموذج أمن الشبكات"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 9: "أمان تطبيق الويب"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 10: "التنفيذ الرمزي"
الجزء 1 /
الجزء 2 /
الجزء 3 الآن ، بعد الفرع لأسفل ، نرى التعبير t = y. نظرًا لأننا نفكر في مسار واحد في كل مرة ، فليس علينا إدخال متغير جديد لـ t. يمكننا ببساطة القول أنه بما أن t = y ، فإن t لم تعد 0.
نواصل التحرك لأسفل ونصل إلى النقطة التي نصل فيها إلى فرع آخر. ما هو الافتراض الجديد الذي يجب علينا القيام به من أجل متابعة هذا المسار؟ هذا افتراض أن t <y.
ما هو ر؟ إذا بحثت عن الفرع الصحيح ، فسوف نرى ذلك t = y. وفي جدولنا ، T = y و Y = y. ويترتب منطقياً على ذلك أن تقييدنا يبدو مثل y <y ، والذي لا يمكن أن يكون.
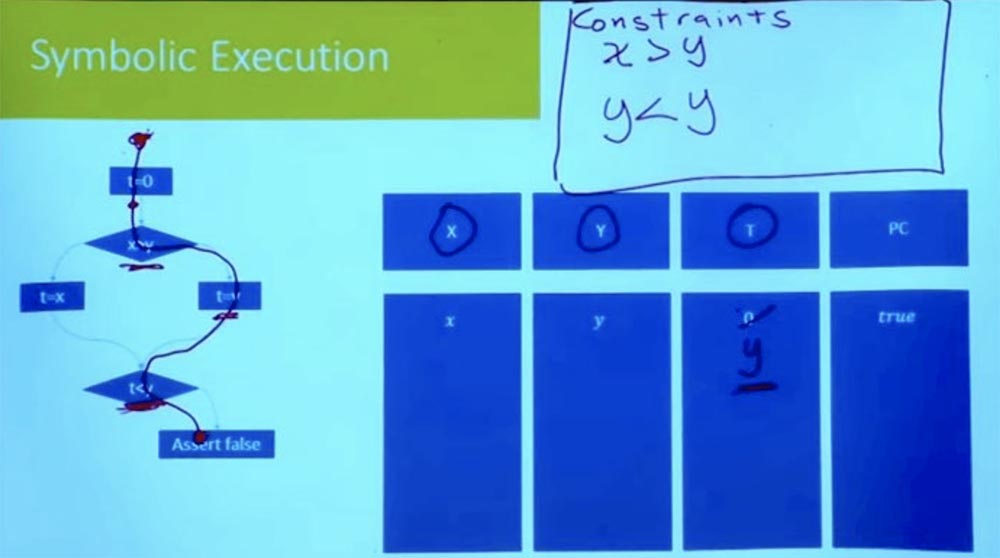
وبالتالي ، كان لدينا كل شيء بالترتيب حتى وصلنا إلى هذه النقطة t <y. حتى نصل إلى بيان كاذب ، لدينا جميع أوجه عدم المساواة التي يجب أن تكون صحيحة. لكن هذا لا يعمل ، لأنه عند أداء مهام الفرع الصحيح ، لدينا تناقض منطقي.
لدينا ما يسمى غالبًا بحالة المسار. يجب أن يكون هذا الشرط صحيحًا حتى يسير البرنامج بهذه الطريقة. لكننا نعلم أن هذا الشرط لا يمكن الوفاء به ، لذلك من المستحيل أن يسير البرنامج على هذا النحو. لذلك تم القضاء على هذا المسار الآن تمامًا ، ونعلم أنه لا يمكن تجاوز هذا المسار الصحيح.
ماذا عن الطريقة الأخرى؟ دعونا نحاول أن نتصفح الفرع الأيسر بطريقة مختلفة. ماذا ستكون شروط هذا المسار؟ مرة أخرى ، تبدأ حالتنا الرمزية عند t = 0 ، و X و Y يساويان المتغيرات x و y.

ما هو تقييد المسار الآن في هذه الحالة؟ نشير إلى الفرع الأيسر على أنه صحيح ، والفرع الأيمن على أنه خطأ ونعتبر كذلك القيمة t = x. نتيجة للمعالجة المنطقية للظروف t = x و x> y و t <y ، نحصل على ما لدينا في نفس الوقت ما x> y و x <y.
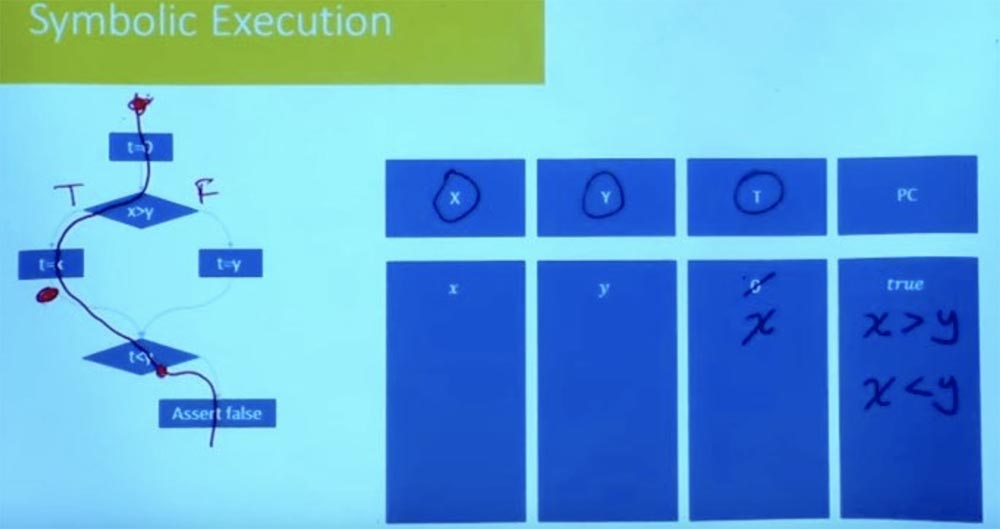
من الواضح أن هذه الحالة من المسار غير مرضية. لا يمكن أن يكون لدينا x أكبر من وأصغر من y. لا يوجد تخصيص لمتغير X يفي بالقيدين. وهكذا ، يخبرنا هذا أن الطريقة الأخرى غير مرضية أيضًا.
اتضح أننا في هذه اللحظة اكتشفنا جميع المسارات الممكنة في البرنامج التي يمكن أن تقودنا إلى هذه الحالة. يمكننا في الواقع أن نثبت ونتحقق من عدم وجود طريقة ممكنة تقودنا إلى البيان الكاذب.
الجمهور: في هذا المثال ، أظهرت أنك درست تقدم البرنامج عبر جميع الفروع الممكنة. لكن إحدى مزايا التنفيذ الرمزي هي أننا لسنا بحاجة إلى دراسة جميع المسارات الأسية الممكنة. فكيف لتجنب هذا في هذا المثال؟
البروفيسور: هذا سؤال جيد جدا. في هذه الحالة ، ستقوم بالتوفيق بين تنفيذ الأحرف ومدى الدقة التي تريدها. لذلك في هذه الحالة ، نحن لا نستخدم الكثير من التنفيذ الرمزي كما في المرة الأولى التي نظرنا فيها إلى تدفق البرنامج على كلا الفرعين في وقت واحد. ولكن بفضل هذا ، أصبحت قيودنا بسيطة للغاية.
القيود الفردية "واحدة تلو الأخرى" بسيطة للغاية ، ولكن عليك القيام بذلك مرارًا وتكرارًا ، ودراسة جميع الفروع القائمة ، وبشكل أسي - وجميع الطرق الممكنة.
هناك العديد من المسارات بشكل كبير ، ولكن لكل مسار ككل ، هناك أيضًا مجموعة كبيرة جدًا من بيانات الإدخال التي يمكن أن تسير في هذا المسار. لذلك يمنحك هذا بالفعل ميزة كبيرة ، لأنه بدلاً من تجربة كل المدخلات الممكنة ، تحاول أن تجرب كل طريقة ممكنة. لكن هل يمكنك فعل شيء أفضل؟
هذا هو أحد المجالات التي تم فيها إجراء الكثير من التجارب فيما يتعلق بالتنفيذ الرمزي ، على سبيل المثال ، التنفيذ المتزامن لعدة مسارات. في مواد المحاضرة ، اجتمعت مع الاستدلال ومجموعة من الاستراتيجيات التي استخدمها المجربون لجعل البحث أكثر قابلية للحل.
على سبيل المثال ، أحد الأشياء التي يفعلونها هو أنهم يستكشفون طريقة تلو الأخرى ، ولكن لا يفعلون ذلك بشكل عمياء تمامًا. يتحققون من ظروف المسار بعد كل خطوة يتم اتخاذها. لنفترض هنا في برنامجنا ، بدلاً من قول "خطأ" ، سيكون هناك شجرة معقدة من البرامج ، رسم بياني للتحكم في التدفق.
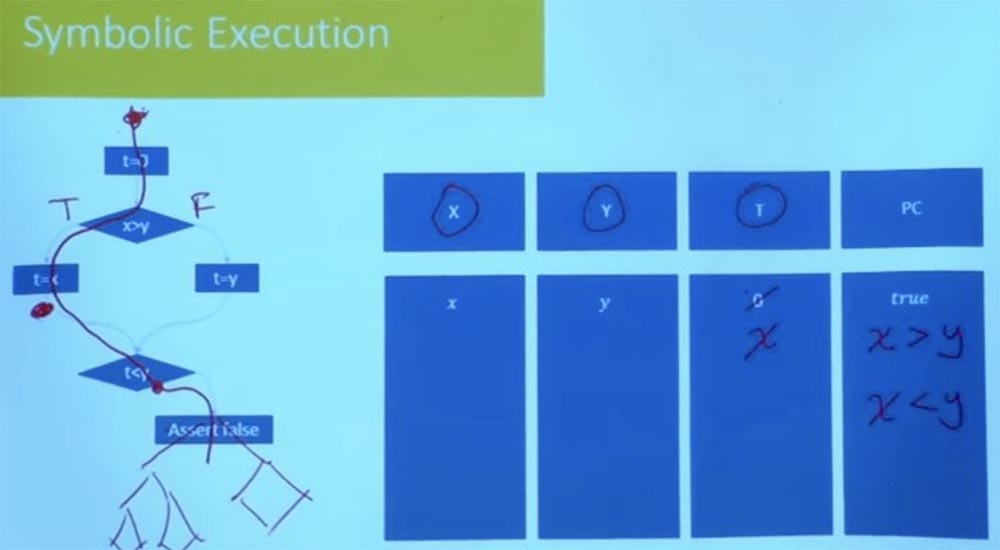
لا تحتاج إلى الانتظار حتى تصل إلى النهاية للتحقق من أن هذا المسار ممكن. في تلك اللحظة ، عندما تصل إلى الشرط t <y ، فأنت تعلم بالفعل أن هذا المسار غير مرض ، ولن تسير أبدًا في هذا الاتجاه. لذلك ، فإن قطع الفروع الخاطئة في بداية البرنامج يقلل من كمية العمل التجريبي. يمنع الاستكشاف المعقول للمسار من احتمال فشل البرنامج في المستقبل. تبدأ العديد من الأدوات العملية المستخدمة اليوم في المقام الأول باختبار عشوائي للحصول على المجموعة الأولية من المسارات ، وبعد ذلك سيبدأون في استكشاف المسارات في الحي. يعالجون العديد من الخيارات للتنفيذ المحتمل للبرنامج لكل من الفروع ، ويتساءلون عما يحدث في هذه المسارات.
إنه مفيد بشكل خاص إذا كان لدينا مجموعة جيدة من الاختبارات. قم بإجراء الاختبار وتجد أن هذا الجزء من التعليمات البرمجية لا يتم تنفيذه. لذلك ، يمكنك أن تأخذ المسار الذي اقترب من تنفيذ الكود وأن تسأل ما إذا كان يمكن تغيير هذا المسار بحيث يسير في الاتجاه الصحيح؟

ولكن في اللحظة التي تحاول فيها جعل كل المسارات في نفس الوقت ، تبدأ القيود تصبح مستعصية على الحل. لذلك ، ما يمكنك القيام به هو أداء وظيفة واحدة في كل مرة ، بينما يمكنك معرفة جميع المسارات في وظيفة معًا. إذا حاولت إنشاء كتل كبيرة ، فيمكنك بشكل عام استكشاف جميع الطرق الممكنة.
الشيء الأكثر أهمية هو أنه بالنسبة لكل فرع ، يمكنك التحقق من القيود الخاصة بك وتحديد ما إذا كان هذا الفرع يمكن أن يسير في كلا الاتجاهين. إذا لم تتمكن من اتباع كلا المسارين ، يمكنك توفير الوقت والجهد من خلال عدم اتباع الاتجاه الذي لا يمكنها الذهاب إليه. بالإضافة إلى ذلك ، لا أتذكر الإستراتيجيات المحددة التي يستخدمونها للعثور على طرق من المرجح أن تؤدي إلى نتائج جيدة جدًا. لكن قطع الفروع الخاطئة في المرحلة الأولية مهم جدًا.
حتى الآن ، كنا نتحدث بشكل أساسي عن "كود اللعبة" ، عن المتغيرات الصحيحة ، عن الفروع ، عن أشياء بسيطة للغاية. ولكن ماذا يحدث عندما يكون لديك برنامج أكثر تعقيدًا؟ على وجه الخصوص ، ماذا يحدث عندما يكون لديك برنامج يتضمن مجموعة؟

من الناحية التاريخية ، كانت كومة الورك لعنة تحليل جميع البرامج ، لأن الأشياء النظيفة والأنيقة في وقت فورتران تنفجر تمامًا عندما تحاول تشغيلها باستخدام برامج C التي تخصص فيها الذاكرة لليسار واليمين. يوجد لديك تراكبات وكل الفوضى المرتبطة بالبرنامج مع ذاكرة مخصصة ومؤشرات حسابية. هذا هو أحد المجالات التي يتمتع فيها التنفيذ الرمزي بقدرة رائعة على التفكير في البرامج.
فكيف نفعل ذلك؟ دعونا ننسى الفروع والتحكم في التدفق للحظة. لدينا برنامج بسيط هنا. يخصص بعض الذاكرة ، ويلغيها ، ويحصل على مؤشر جديد y من المؤشر x. ثم تكتب شيئًا لـ y وتتحقق مما إذا كانت القيمة المخزنة في المؤشر y تساوي القيمة المخزنة في المؤشر x؟
استنادًا إلى المعرفة الأساسية بـ C ، يمكنك أن ترى أن هذا الفحص لم يتم إجراؤه لأن x تمت إعادة تعيينه و y = 25 ، لذلك يشير x إلى موقع مختلف. كل شيء على ما يرام حتى الآن.
تستخدم الطريقة التي نمثل بها كومة الذاكرة المؤقتة ، وطريقة تصميم كومة الذاكرة المؤقتة في معظم الأنظمة ، تمثيل الكومة في C ، حيث تكون مجرد قاعدة عناوين ضخمة ، وهي مجموعة ضخمة يمكنك من خلالها وضع بياناتك.
هذا يعني أنه يمكننا تمثيل برنامجنا كمجموعة بيانات عالمية كبيرة جدًا ، والتي ستسمى MEM. هذه مصفوفة ستعمل بشكل أساسي على تعيين العناوين للقيم. العنوان عبارة عن قيمة 64 بت فقط. وماذا سيحدث بعد قراءة شيء من هذا العنوان؟ يعتمد ذلك على كيفية نمذجة الذاكرة.
إذا قمت بوضع نموذج لها على مستوى البايت ، فستحصل على بايت. إذا قمت بوضع نموذج لها على مستوى الكلمة ، فستحصل على كلمة. اعتمادًا على نوع الأخطاء التي تهتم بها ، واعتمادًا على ما إذا كنت قلقًا بشأن تخصيص الذاكرة أم لا ، ستقوم بوضع نموذج لها بشكل مختلف قليلاً ، ولكن عادةً ما تكون الذاكرة مجرد مصفوفة من العنوان إلى القيمة.

لذا فإن العنوان مجرد عدد صحيح. بطريقة ما ، لا يهم ما يعتقده C عن العنوان ، إنه مجرد عدد صحيح 64 بت أو 32 بت ، اعتمادًا على جهازك. إنها ببساطة قيمة مفهرسة في هذه الذاكرة. وما يمكنك وضعه في الذاكرة ، يمكنك القراءة من تلك الذاكرة.
لذلك ، تصبح أشياء مثل حساب المؤشر مجرد حساب صحيح. من الناحية العملية ، هناك بعض الصعوبات ، لأنه في C ، يعرف حساب المؤشر عن أنواع المؤشر ، وسوف تزداد بما يتناسب مع الحجم. لذا فإن النتيجة التي نحصل عليها هي خط مثل هذا:
y = x + 10 ؛ حجم (عدد)

ولكن ما يهم حقًا هو ما يحدث عندما تكتب وتقرأ من الذاكرة. استنادًا إلى المؤشر الذي يجب كتابة 25 فيه y ، آخذ مصفوفة من الذاكرة وفهرستها باستخدام y. وأكتب 25 إلى موقع الذاكرة هذا.
ثم أنتقل إلى العبارة MEM [y] = MEM [x] ، وقراءة القيمة من الموقع y في الذاكرة ، وقراءة القيمة من الموقع x في الذاكرة ، ومقارنتها مع بعضها البعض. لذا أتحقق مما إذا كانت تتطابق أم لا.
هذا افتراض بسيط للغاية ، يسمح لك بالتبديل من برنامج يستخدم كومة الذاكرة المؤقتة إلى برنامج يستخدم هذا الصفيف العملاق العملاق الذي يمثل الذاكرة. هذا يعني أنه عند الحديث عن البرامج التي تدير كومة الذاكرة المؤقتة ، فأنت لا تحتاج حقًا إلى التحدث عن البرامج التي تدير كومة الذاكرة المؤقتة. ستتمكن بشكل مثالي من التحدث عن المصفوفات ، وليس عن الأكوام.
هنا سؤال بسيط آخر. ماذا عن وظيفة malloc؟ يمكنك فقط استخدام وتنفيذ malloc في C ، وتتبع جميع الصفحات المميزة ، وتتبع كل ما تم تحريره ، ولديك قائمة مجانية ، وهذا يكفي. اتضح أنه بالنسبة للعديد من الأغراض ولأنواع عديدة من الأخطاء ، لا تحتاج إلى أن يكون المعقد معقدًا.
في الواقع ، يمكنك التبديل من malloc ، الذي يبدو كالتالي: x = malloc (sizeof (int) * 100) ، إلى malloc من هذا النوع:
نقطة البيع = 1
Int malloc (int n) {
rv = نقطة البيع
POS + = n ؛
}}
الذي يقول ببساطة: "سأقوم بحفظ العداد للمساحة الحرة التالية في الذاكرة ، وكلما طلب شخص ما عنوانًا ، أعطيه هذا الموقع وزد هذا الموضع ، ثم أعيد رف." في هذه الحالة ، ما يتم تجاهل مالوك بالمعنى التقليدي تمامًا.

في هذه الحالة ، لا يوجد إطلاق للذاكرة. تستمر الوظيفة ببساطة في التحرك أكثر فأكثر من الذاكرة ، وأكثر ، وأكثر ، وهذا هو المكان الذي تنتهي فيه دون أي تحرير. كما أنها لا تهتم حقًا بأن هناك مناطق من الذاكرة لا تستحق الكتابة فيها ، لأن هناك عناوين خاصة ذات أهمية خاصة محفوظة لنظام التشغيل.
إنه لا يصمم أي شيء يجعل كتابة وظيفة malloc معقدة ، ولكن فقط عند مستوى معين من التجريد ، عندما تحاول التحدث عن نوع من التعليمات البرمجية المعقدة التي تؤدي إلى التلاعب بالمؤشر.
في الوقت نفسه ، لا تهتم بتحرير الذاكرة ، ولكنك قلق بشأن ما إذا كان البرنامج سيكتب ، على سبيل المثال ، خارج المخزن المؤقت ، وفي هذه الحالة يمكن أن تكون وظيفة malloc جيدة جدًا.

وهذا يحدث بالفعل في كثير من الأحيان عندما تقوم بتنفيذ رمزي حقيقي للكود. خطوة مهمة للغاية هي نمذجة وظائف مكتبتك. سيكون للطريقة التي تصمم بها وظائف المكتبة تأثيرًا كبيرًا ، من ناحية ، على أداء التحليل وقابليته للتوسع ، ولكن من ناحية أخرى ، ستؤثر أيضًا على الدقة.
لذلك إذا كان لديك مثل هذا النموذج "لعبة" ، مثل هذا ، سوف يعمل بسرعة كبيرة ، ولكن في نفس الوقت سيكون هناك أنواع معينة من الأخطاء التي لا يمكنك ملاحظتها. لذلك ، على سبيل المثال ، في هذا النموذج ، أتجاهل تمامًا التوزيعات ، لذلك قد أحصل على خطأ إذا حصل شخص ما على مساحة غير مخصصة. لذلك ، في الحياة الواقعية ، لن أستخدم أبدًا نموذج Mickey Mouse malloc هذا.
لذا فهو دائمًا توازن بين دقة التحليل والكفاءة. وكلما زادت تعقيد نماذج الوظائف القياسية ، مثل الحصول على malloc ، قل تحليلها للتحجيم. ولكن بالنسبة لبعض فئات الأخطاء ، ستحتاج إلى هذه النماذج البسيطة. لذلك ، تعد المكتبات المختلفة في لغة C ذات أهمية كبيرة ، وهي ضرورية لفهم ما يفعله هذا البرنامج بالفعل.
لذلك ، قللنا مشكلة التفكير في الكومة عن طريق التفكير في البرنامج باستخدام المصفوفات ، لكنني لم أخبرك حقًا كيف تتحدث عن البرنامج مع المصفوفات. اتضح أن معظم مذيبات SMT تدعم نظرية المصفوفة.

الفكرة هي أنه إذا كان a صفيفًا ، فهناك بعض الترميز الذي يسمح لك بأخذ هذا الصفيف وإنشاء صفيف جديد ، حيث يتم تحديث الموقع i إلى القيمة e. هل هذا واضح؟
لذلك ، إذا كان لدي مصفوفة a ، وقمت بعملية التحديث هذه ، ثم حاولت قراءة قيمة k ، فهذا يعني أن قيمة k ستكون مساوية لقيمة k في المصفوفة a ، إذا كانت k مختلفة عن i ، وستكون مساوية لـ e ، إذا كان k يساوي i.
يعني تحديث المصفوفة أنك بحاجة إلى أخذ المصفوفة القديمة وتحديثها بمصفوفة جديدة. حسنًا ، إذا كان لديك صيغة تتضمن نظرية المصفوفات ، لهذا السبب بدأت بمصفوفة صفرية ، والتي يتم تمثيلها في كل مكان ببساطة بالأصفار.

ثم أكتب 5 إلى الموقع i و 7 إلى الموقع j ، وبعد ذلك قرأت من k وتحقق مما إذا كانت 5 أم لا. ثم يمكن توسيعه باستخدام تعريف شيء ما ، على سبيل المثال: "إذا كان k هو i و k هو y ، بينما كان k مختلفًا عن j ، ثم نعم ، فسيكون 5 ، وإلا فلن 5 ".
وعمليًا ، لا تقوم مذيبات SMT بتوسيع هذا إلى العديد من الصيغ المنطقية فحسب ، بل يستخدمون هذه الاستراتيجية ذهابًا وإيابًا بين حلال SAT والمحرك ، القادر على التحدث عن نظرية الصفيف لتنفيذ هذا العمل.
الشيء المهم هو أنه بالاعتماد على نظرية المصفوفات هذه ، باستخدام نفس الاستراتيجية التي طبقناها لإنشاء صيغ للأعداد الصحيحة ، يمكنك في الواقع إنشاء صيغ تتضمن منطق المصفوفة ، تحديثات المصفوفة ، محاور المصفوفة ، تكرار المصفوفات. وطالما أنك تقوم بتصحيح مسارك ، فمن السهل جدًا إنشاء هذه الصيغ.
إذا لم تقم بتصحيح المسارات الخاصة بك ، ولكنك تريد إنشاء صيغة تتوافق مع مرور البرنامج على جميع المسارات ، فإن هذا سهل نسبيًا أيضًا. الشيء الوحيد الذي عليك التعامل معه هو نوع خاص من الحلقات.
من السهل جدًا تصميم القواميس والخرائط باستخدام وظائف غير محددة. في الواقع ، نظرية المصفوفات نفسها ليست سوى حالة خاصة لوظيفة غير محددة. بمساعدة هذه الوظائف ، يمكن القيام بأشياء أكثر تعقيدًا. في حل SMT الحديث ، هناك دعم مدمج للتفكير حول المجموعات وعمليات المجموعة ، والتي يمكن أن تكون مفيدة جدًا إذا كنت تتحدث عن برنامج يتضمن حساب المجموعات.
عند تصميم إحدى هذه الأدوات ، تكون مرحلة النمذجة مهمة جدًا. والنقطة ليست فقط كيفية نمذجة وظائف البرنامج المعقدة وصولاً إلى نظرياتك ، على سبيل المثال ، أشياء مثل تقليل الأكوام إلى المصفوفات. والنقطة هي أيضًا النظريات والمحللات التي تستخدمها. هناك عدد كبير من النظريات والمحللين بعلاقات مختلفة ، والتي من الضروري اختيار حل وسط معقول بين الكفاءة والتكلفة.

تلتزم معظم الأدوات العملية بنظرية ناقلات البتات ، وإذا لزم الأمر ، يمكن استخدام نظرية المصفوفات لنمذجة أكوام. بشكل عام ، تحاول الأدوات العملية تجنب نظريات أكثر تعقيدًا ، مثل نظرية المجموعات. هذا لأنه عادة ما يكون أقل قابلية للتطوير في بعض الحالات ، إذا كنت لا تتعامل مع برنامج يتطلب أدوات من هذا النوع للعمل.
الجمهور: بالإضافة إلى دراسة الأداء الرمزي ، ما الذي يركز عليه المطورون؟
: — , . , , , , . , .
, , . , , , , , , , .
, — , , . , , — , JavaScript Python, . , .

, Python. , , : «, , , ». .
, , , , , .
, , , - , , .
, , , . , , Microsoft Word, , , .
, , , , .
, . , , - , - . , , . , .
النسخة الكاملة من الدورة متاحة
هنا .
شكرا لك على البقاء معنا. هل تحب مقالاتنا؟ هل تريد رؤية مواد أكثر إثارة للاهتمام؟ ادعمنا عن طريق تقديم طلب أو التوصية به لأصدقائك ،
خصم 30 ٪ لمستخدمي Habr على نظير فريد من خوادم مستوى الدخول التي اخترعناها لك: الحقيقة الكاملة حول VPS (KVM) E5-2650 v4 (6 نوى) 10GB DDR4 240GB SSD 1Gbps من 20 $ أو كيفية تقسيم الخادم؟ (تتوفر الخيارات مع RAID1 و RAID10 ، حتى 24 مركزًا وحتى 40 جيجابايت DDR4).
VPS (KVM) E5-2650 v4 (6 نوى) 10GB DDR4 240GB SSD 1Gbps حتى ديسمبر مجانًا عند الدفع لمدة ستة أشهر ، يمكنك الطلب
هنا .
ديل R730xd أرخص مرتين؟ 2 Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 $249 ! اقرأ عن
كيفية بناء مبنى البنية التحتية الطبقة باستخدام خوادم Dell R730xd E5-2650 v4 بتكلفة 9000 يورو مقابل سنت واحد؟