معهد ماساتشوستس للتكنولوجيا. محاضرة رقم 6.858. "أمن أنظمة الكمبيوتر." نيكولاي زيلدوفيتش ، جيمس ميكنز. 2014 سنة
أمان أنظمة الكمبيوتر هي دورة حول تطوير وتنفيذ أنظمة الكمبيوتر الآمنة. تغطي المحاضرات نماذج التهديد ، والهجمات التي تهدد الأمن ، وتقنيات الأمان بناءً على العمل العلمي الحديث. تشمل الموضوعات أمان نظام التشغيل (OS) ، والميزات ، وإدارة تدفق المعلومات ، وأمان اللغة ، وبروتوكولات الشبكة ، وأمان الأجهزة ، وأمان تطبيقات الويب.
المحاضرة 1: "مقدمة: نماذج التهديد"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 2: "السيطرة على هجمات القراصنة"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 3: "تجاوزات العازلة: المآثر والحماية"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 4: "فصل الامتيازات"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 5: "من أين تأتي أنظمة الأمن؟"
الجزء 1 /
الجزء 2المحاضرة 6: "الفرص"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 7: "وضع حماية العميل الأصلي"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 8: "نموذج أمن الشبكات"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 9: "أمان تطبيق الويب"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 10: "التنفيذ الرمزي"
الجزء 1 /
الجزء 2 /
الجزء 3 الجمهور: يبدو أنك لم تتحدث عن كيفية استخدام البتات لتخزين عدد صحيح.
البروفيسور: هذا سؤال جيد جدا. ويتعلق الأمر حقًا بكيفية تحديد حدودك ، أليس كذلك؟ لذلك ، إذا نظرت إلى مثالنا البسيط منذ البداية ، سترى أننا افترضنا وجود أعداد صحيحة درسناها في المدرسة الابتدائية. في الوقت نفسه ، قررنا تمامًا تجاهل أخطاء تجاوز السعة. إذا كنت تهتم بأخطاء تجاوز السعة ، ومن المهم بالنسبة لك أنه لا توجد مثل هذه الأخطاء ، فإن استخدام الأرقام الصحيحة رياضياً لن يساعد في حل المشكلة.

ما تحتاجه هو تقديم هذه الكميات ليس كأعداد صحيحة ، ولكن كمتجهات بت. عندما تقوم بتمثيلها كمتجهات صغيرة ، يجب عليك استخدام رؤية أوسع للأشياء. هنا نعود إلى مذيبات SMT. أحد جوانب النظرية المعيارية هو أن حلالا نفسه قابل للتوسيع باستخدام نظريات مختلفة.
النظريات الأكثر شعبية هي نظريات متجهة طولية ثابتة. هذا يعني أنه إذا قمت بتفسير الصيغ الخاصة بك في نظرية متجهات البت ذات الطول الثابت ، يجب عليك أولاً تعيين طول متجهات البت. بمعنى ، يجب أن تشير صراحةً إلى أنه سيتم استخدام هذا لمتجهات البت التي يبلغ طولها 32 بت أو 8 بت أو 64 بت.

هناك نظرية أخرى تسمى نظرية مجموعة TOA. وسوف نتحدث أكثر عن ذلك. على عكس نظرية ناقلات البتات ، المصممة لأشياء ذات طول ثابت ، فإن نظرية المصفوفات مخصصة للمجموعات التي يكون حجمها غير معروف مسبقًا.
الآن ، من الناحية العملية ، لا أحد يستخدم نظرية المصفوفات ، على سبيل المثال ، لنمذجة الأعداد الصحيحة ، لأنها مكلفة للغاية. إن الحديث عن مشكلة أكثر تكلفة بكثير عندما لا تعرف حدودها. لذلك ، كقاعدة عامة ، يستخدم الناس نظرية طول ثابت لمتجهات البت في المناقشات حول الأعداد الصحيحة أو حتى الرموز.
نظرية أخرى واسعة الانتشار هي نظرية الحساب الحقيقي الصحيح ، وخاصة الحساب الصحيح الخطي.

الناس مغرمون جدًا بهذه النظرية لأنها توفر حجة فعالة ، ولكنها ليست جيدة جدًا عندما تتحدث عن البرامج ، لأنك هنا تهتم حقًا بمشاكل الفائض. لكن هذه النظرية تستخدم على نطاق واسع لأشياء كثيرة.
نظرية أخرى غالبًا ما تستخدم هي نظرية الوظائف غير المترجمة. ماذا تعني هذه النظرية؟

هذا يعني أن لديك صيغة معينة. في هذه الصيغة ، أنت تعرف أنك تستدعي وظيفة ، لكنك لا تعرف شيئًا عن هذه الوظيفة باستثناء حقيقة أنه إذا قمت بإدخال بعض المدخلات فيها ، فستحصل على نفس الناتج.
اتضح أن هذا مفيد جدًا عند التفكير في أشياء مثل استخدام رمز النقطة العائمة ، والنمذجة ، والجيب ، وجيب التمام ، والجذور التربيعية. يمكن أن تكون المناقشات التفصيلية حول هذه الأشياء مستهلكة للوقت ومكلفة للغاية. لكن استخدام هذه النظرية يسمح لك بالقول: "انظر ، أنا لا أهتم حقًا بما تفعله دالة الجيب. لا يهمني ما ستعطيه بالضبط. أحتاج فقط إلى معرفة أنه إذا قمت باستدعاء دالة الجيب في أماكن مختلفة من البرنامج بإدخال محدد ، فسوف أحصل على بيانات من نفس النوع عند الإخراج. هذا يكفي بالنسبة لي للتفكير في برنامجي ".
وبالتالي ، فإن العمليات الأكثر شيوعًا في تحليل الأنظمة الحقيقية هي ناقلات البتات التي تعمل مع الأعداد الصحيحة والسجلات والمؤشرات. في الواقع ، غالبًا ما يتم تمثيل المؤشرات بواسطة عدد صحيح ، لأنه في بعض الأحيان لا تقوم بتعيين متجهات البت على المؤشرات. لكن في بعض الأحيان عليك القيام بذلك ، وبعد ذلك لا يمكنك استخدام الأعداد الصحيحة.
لذا ، قمنا بفحص ما يمكن أن تفعله أداة حل SMT لك. كيف يعمل حقا؟ ما بداخلهم ما يجعلهم يعملون؟
في الواقع ، يعتمد محللو SMT على قدرتنا على حل مشكلات الجدوى للصيغ المنطقية SAT ، على القدرة على النظر في المشكلات المرتبطة فقط بالقيود المنطقية البحتة والمتغيرات المنطقية ، وإخبارنا ما إذا كنت ستضمن أن البرنامج يعين القيم المعينة لهذه المتغيرات المنطقية أم لا .
هذا شيء قام لسنوات عديدة بتدريس الطلاب الكبار ، قائلين إن هذه في الواقع مهمة كاملة NP ، وفي الحالات التي يتعلق بها شيء ما في SAT ، يجب ألا تفعل ذلك. ولكن اتضح أن لدينا بالفعل مذيبات SAT جيدة جدًا.
لذا ، سأخبرك بالفكرة الأساسية لكيفية عمل مذيبات SAT. يكمن في حقيقة أنك تأخذ كل قيودك على المتغيرات المنطقية وتضعها في قاعدة البيانات. قد لا تتمكن من رؤية الحروف الصغيرة على الشاشة بوضوح ، ولكن هذا كل ما يمكنني فعله.

سوف أعلق وأتحدث عنه في سياق الإجراء ، وبعد ذلك سأنشر الشرائح حتى تتمكن من رؤية ما هو مكتوب هناك.
لذا ، هنا في مهمة SAT لدينا كل هذه المتغيرات التي تمثل المجهولات المنطقية ، أليس كذلك؟ نريد أن نعرف ما إذا كان من الممكن أن تكون X صحيحة في نفس الوقت (X = TRUE) ، وأن تكون Y صحيحة ، وأن تكون Z صحيحة. هؤلاء هم مجهولون. علاوة على ذلك ، فإن جميع القيود في شكل اقتران عادي. هذا يعني أن كل قيودنا هي إما X1 = true أو X2 = true أو X3 = true.

في هذا النموذج ، لدينا كل قيودنا ، التي تقول إما أن X1 صحيحة ، أو X2 خاطئة ، أو X3 خاطئة. ربما تتذكر من الرياضيات المنفصلة أنه يمكن تمثيل أي صيغة منطقية في شكل ضام عادي. هذا يعني أن أي تمثيل تستخدمه لتمثيل الصيغ المنطقية ، يمكنك بسهولة التحويل إلى هذا التنسيق.
لذلك ، لدينا قاعدة بيانات مع العديد من القيود على هذا النموذج. سيختار محلل SAT أحد هذه المتغيرات بشكل عشوائي ، بافتراض أنه X1. فيقول: "لماذا لا تضبط X1 على الحقيقة؟ لا أعرف شيئًا عن هذه القيود ، لذا يمكنني أن أفترض أن هذا الأمر كذلك حقًا ". ثم يحدث أنه سيكون لديك قيود ، على سبيل المثال ، تنص على أن X1 خطأ أو X7 صحيح.
لذا ، إذا كنت تعرف أن X1 صحيحة وتعلم أن X1 خطأ أو X7 صحيح ، فماذا تعرف عن X7؟
الجمهور: يجب أن يكون صحيحا!
الأستاذ: نعم ، يجب أن يكون صحيحا. لأنه بخلاف ذلك لن يتم الوفاء بهذا القيد. لذا ، الآن قمت بتوزيع هذه القيمة من X1 إلى X7. لنفترض أنك حددت الآن متغيرًا عشوائيًا آخر ، مثل X5.

لنفترض الآن أن لديك تقييدًا يقول: إما أن X7 خطأ ، أو X6 صحيح ، أو X5 خطأ. لذا ، لدي X5 = true و X7 = true. هذا يعني أن X6 يجب أن يكون الآن صحيحًا أيضًا. لأنه بخلاف ذلك سيتم انتهاك هذا القيد. لذا ، يخلص النظام إلى أن X6 يجب أن يكون صحيحًا ، ويستمر في العملية ، وإجراء الفحوصات المتاحة والنظر في جميع العروض المتاحة. يتحقق النظام مما إذا كانت هناك أشياء أخرى تتضمنها عمليات الفحص التي يمتلكها. وتتبع هذه المعاني حتى يحدث أحد شيئين.
الأول هو أنك تستمر في متابعة العواقب وتجربة أشياء عشوائية ، وفي النهاية تقوم بتعيين القيمة لكل متغير دون مواجهة تناقض. لذا فعلت كل شيء بشكل صحيح.
الثاني - أنك تواجه تناقضًا ، ثم تعود إلى الحالة التي جعلت X4 صحيحًا ، باستثناء الحالة التي جعلت X4 خاطئة. ولكن هناك قاعدة واحدة للجبر البولي يجب أن يعرفها الجميع: لا يمكن أن يكون المتغير صحيحًا وخطأًا في نفس الوقت.

وتقول أنك تواجه تناقضًا ، من الواضح أنك فعلت شيئًا خاطئًا في إحدى هذه المهام العشوائية التي حاولت إكمالها.
دعونا نحلل هذا التناقض ونرى أي نوع من المهام أدى إلى هذا التناقض. استنادًا إلى المهام التي أدت إلى هذا التناقض ، دعونا نخرج ببند تعارض جديد يلخص هذا التناقض.
ماذا يحدث أن X1 خطأ ، و X5 خطأ ، و X9 خطأ أيضًا؟ يعتمد هذا بشكل أساسي على ما تعلمته من هذه المهام العشوائية ، والتي اكتشفت خلالها أن أحد هذه الأشياء يجب أن يكون صحيحًا ، وأنه لا يمكن أن يكون X1 صحيحًا و X5 صحيحًا ، و X9 كان خطأ ، لا يمكن أن يكون هذا.
أعلم أن هذا لا يمكن أن يحدث ، لأنه عندما حاولت القيام بذلك ، "انفجر" كل شيء ، أنهيت البرنامج بتناقض.
وهكذا ، يحاول SAT حلالا إكمال المهام العشوائية ، والتحقق من كيفية سيرها. عندما يواجه التناقضات ، يحلل مجموعة العواقب التي أدت إلى هذه التناقضات ، ويشكل في نهاية المطاف قيودًا جديدة ، والتي تضمن ألا يواجه المحلل هذا التناقض الخاص مرة أخرى ، هذه المشكلة بالذات.
وهكذا ، يمكننا أن نتخيل حل SAT على أنه "صندوق أسود" يعطي قيودًا منطقية ويمكننا معرفة ما إذا كان مرضيًا أم لا. تم تصميم مذيبات SMT على رأس أفضل مذيبات SAT. يمكنهم استخدام قوة محللات SAT لحل مشكلات NP-Complete مع التفكير الموجه نحو الموضوع حول النظريات المدعومة.
للحصول على فكرة عن كيفية عمل ذلك ، افترض أن لديك مثل هذه الصيغة.

هل هذا ممكن؟ هل يمكننا إيجاد اختبار مرضي لها؟ يمكن للحل SMT فصل جزء من هذه الصيغة ، الأمر الذي يتطلب المنطق في النظرية الصحيحة. نستخدم الهياكل المنطقية لفصل الصيغ. لذا لدينا الصيغ F1 و F2 و F3 و F4.

الآن هذه مهمة منطقية بحتة - هل يمكنني العثور على مهمة مرضية لذلك؟ يمكن أن يقول حلال SAT: "نعم ، يمكنني العثور على شيء يفي بهذه المهمة عن طريق القيام F1 = true ، F2 = true و F3 = true." هذا يفي بمواصفات الصيغة المنطقية.

\
لذا ، لدينا الآن سؤال يمكننا أن نطرحه على منطقة محددة ، في هذه الحالة هو مجرد حل حسابي خطي. لذا يمكننا أن نذهب إلى Solver Theory solver الخطي ونقول: "SAT solver ينص على أن هذه مهمة معقولة ، وأنه إذا تمكنت من جعل هذه المهمة تعمل ، فستكون صيغتي راضية".
يمكنني القول أن F1 تساوي X> 5 ، و F2 هي Y <5 ، و F3 هي Y> X. لذا يمكنني أن أسأل SAT حلالا إذا كان من الممكن الحصول على مثل X و Y بحيث تكون X> 5 ، و Y هي < 5 ، وفي هذه الحالة سيكون Y> X؟ الآن هذه مسألة حسابية خطية بحتة ، لا يوجد منطق منطقي.
وما هو الجواب على هذا السؤال؟ لا. من المستحيل تلبية هذه الشروط في نفس الوقت.
لذا ، هناك طرق تقليدية لحل المشاكل الخطية. يمكنك استخدام طريقة البسيط ، على سبيل المثال ، لحل أنظمة التفاوتات الخطية. هناك العديد من الطرق التي يمكن استخدامها لحل أنظمة التفاوتات الخطية.
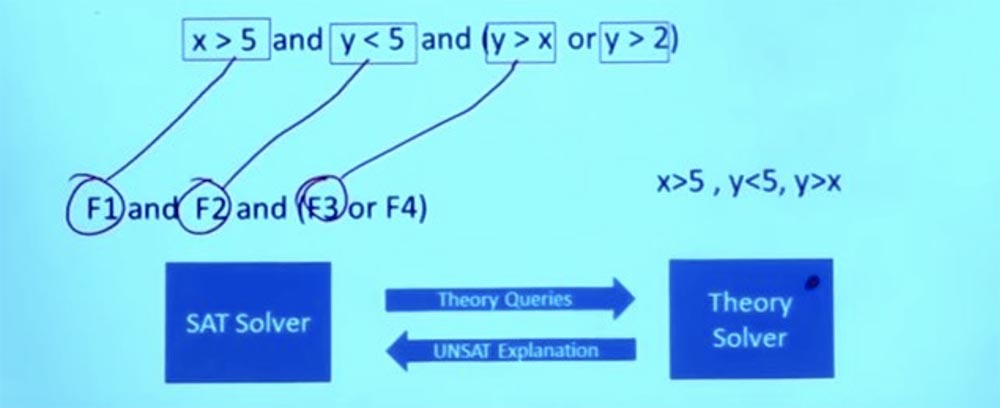
لذا ، يرسل حلال SAT أسئلة نظرية إلى حلال النظرية. خلاصة القول هي أن محللي نظرية حلالا يعرفون كل شيء عن هذه المشاكل ويمكن أن يقدموا إجابة دقيقة على سؤال ما إذا كانت هذه الشروط ستعمل.
في هذه الحالة ، يقوم المحلل النظري بمعالجة الطلب ، ويكتشف أن تعيين الشروط هذا لا يمكن أن يعمل ، ويعود إلى محلل SAT ويقول: "تلك الأشياء التي لم تقم بها لن تعمل"!
لكنه لا يقول فقط نعم أو لا ، ولكنه يفسر سبب عدم نجاح شيء ما. من حقيقة أن هذه الصيغ لا تعمل ، خلصت نظرية حلالا إلى أن F1 و F2 و F3 لا يمكن أن توجد في وقت واحد ، وتقول لـ SAT حلالا أن هذه الصيغ الثلاث حصرية بشكل متبادل.
لذا لدينا الآن بعض المعلومات التي يمكنني الرجوع إليها إلى SAT حلالا وسأله: "مهلا ، يمكنك أن تعطيني حلا يرضي ليس فقط القيد الذي كان لدينا في البداية ، ولكن أيضًا القيد الجديد الذي اكتشفته النظرية حلالا "؟
هل هناك أي غرض آخر يفي الآن بكل من هذه القيود؟
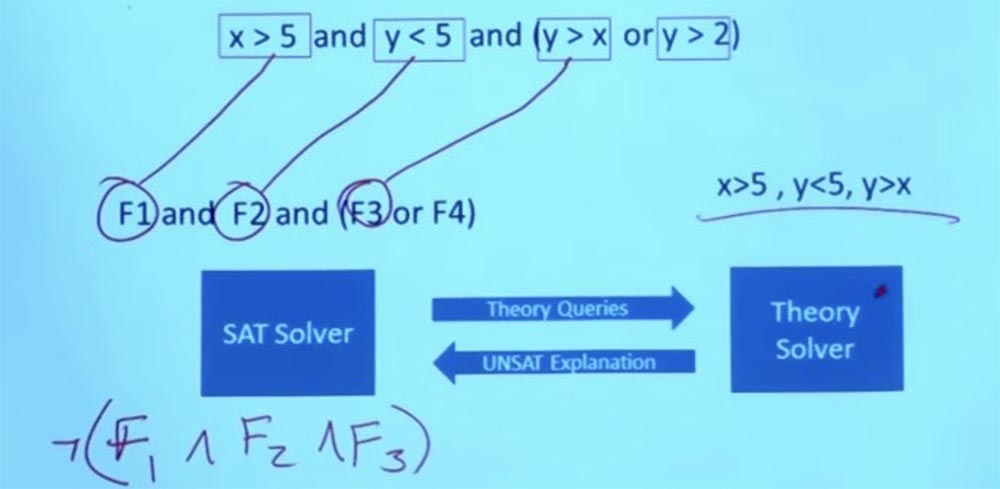
لذا ، فإننا نتجاهل التقييد الأولي X> 5 ، Y <5 ، Y> X ، وهذا لا يزعجنا بعد الآن.
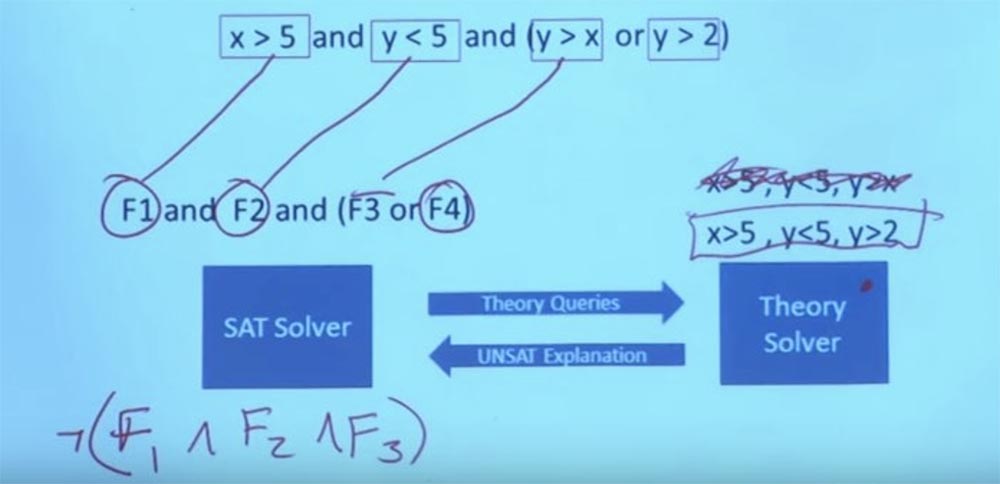
لدينا قيود جديدة يمكننا ضبطها على أداة حل نظريتنا - X> 5 ، Y <5 ، Y> 2. يمكننا جعل Y تساوي 3 ، و X تساوي 6 ، وبعد ذلك ستعمل. الآن لديك مهمة ترضي الصيغة نظريًا وترضي البنية المنطقية لهذا الغرض. وبذلك يمكن للنظام أن يعود ويقول: "نعم ، هذه هي المهمة التي ترضي جميع قيودك". هذا هو التفاعل بين حلال النظرية و حلال SAT. في الواقع ، هذا يعني أن تكون قادرًا على التحدث عن الصيغ المنطقية الكبيرة جدًا والمعقدة جدًا. إليك ما يجعل التنفيذ الرمزي ممكنًا.
الآن سننظر في السؤال التالي - كيف يتم الانتقال من البرنامج إلى القيود التي يمكننا تقديمها إلى SMT حلالا.
الجمهور: هل بناء SMT حلالا NP مكتملة أم لا؟
البروفيسور: إن SMT حلالر هي في الأساس مشكلة كاملة في NP. لكن معظم المحللون في هذه الأيام يتضمنون دعمًا لبعض النظريات غير القابلة للحل تمامًا.
الجمهور: كيف تتعامل مع هذه المشكلة في نظامك؟
البروفيسور: حسنًا ، في النهاية ، ستحصل على قيود تم إنشاؤها من هذا البرنامج. أنت ستعطيها إلى SMT حلالا. وحقيقة أن هذه مهام NP مكتملة أو حقيقة أنها غير مرضية تعني أنه إذا كنت محظوظًا ، فستتلقى إجابة في غضون ثوان. ولكن إذا كنت غير محظوظ ، فقد يستغرق الأمر وقتًا أطول مما استغرقه إنشاء الكون.
 الجمهور:
الجمهور: هل يحدث أن لا تتجاوز مهام النظام الخطي اختبار SAT؟
الأستاذ: نعم ، هذا يحدث بالفعل. ومع ذلك ، فإن الأدوات الهندسية الحالية تجعلها أقل شيوعًا. نحن لا نحل المشكلات العشوائية لـ SAT ، ولا نحل المشكلات العشوائية تمامًا لمتجهات البت.
نحن نحل المشاكل التي لها هيكل معين حتى يتمكن الشخص من النظر إليها والحصول على بعض الثقة في أنها ستعمل. نحن نحاول خلق بعض الحجج في رأسه لفهم سبب نجاح ذلك. ويستخدم محللو SAT هذه البنية. قد تحتوي مشكلتك على مليون متغيرات منطقية ، ولكن في الواقع معظم هذه المتغيرات تعتمد بشكل كبير على قيم بعضها البعض. وبالتالي ، فإن عدد درجات الحرية في المشكلة هو في الواقع أقل بكثير مما تقترحه الملايين من المتغيرات.
الجمهور: تقول أن هذا ليس سؤال امتحان بل واقع الحياة. بمجرد أن يقوم شخص ما ببناء هذا النظام ، يجب أن يعمل ويفهم. لذلك ربما لن يكون هذا أحد الغرائز النظرية غير الضرورية.
الأستاذ: هذا كل شيء. لذلك ، في الممارسة العملية ، عند استخدام هذه الأداة ، ما تفعله دائمًا هو تعيين المهلات. بشكل عام ، يحدث كل شيء لأن الأسي لا يعني أنه لا يمكنك القيام بذلك. الأسي ، أي عندما تكون وظيفة ما محدودة بوظيفة أخرى ، فهذا يعني ببساطة وجود جدار من الطوب أمامه ستعمل هذه الأشياء ، وستعمل بسرعة كبيرة جدًا. يعمل الأسي في كلا الاتجاهين.

عندما تبتعد عن هذا الجدار ، تنمو الأشياء بسرعة كبيرة ، ولكن عندما تقترب من مشاكل أصغر أو أبسط ، فإن هذه المشاكل تتسارع أيضًا بسرعة كبيرة جدًا. هذا يعني أن العديد من المشاكل تنتهي بسرعة كبيرة. ثم تحدث مهلة المشكلة. الهدف هو تصميم الأشياء بحيث من بين المشاكل التي تنتهي بسرعة تلك التي تحقق فوائد عملية. هذه هي المشاكل التي توجهك إلى نقاط الضعف الأمنية لنظامك ، إلى الأخطاء ، إلى المسارات التي ربما لم تستكشفها من قبل ، أو إلى الإدخال الذي ينتهك مساراتك إذا لم تقم بالتحقيق فيها مسبقًا.
لذا ، فنحن نعرف كيف ننتقل من صيغة ، من مجموعة من القيود إلى إجابة إما أن تقول: "نعم ، هذه الصيغة لها حل ، وهذا هو الحل." أو سيقول: "هذه الصيغة غير مرضية ، لأنه لا يوجد مدخلات تفي بمهامك." فكيف نحصل على الصيغة من البرنامج؟
عندما تقوم بتنفيذ رمزي ، تذهب إلى الفرع ولا تعرف في أي اتجاه سيذهب. هناك خياران لما يجب فعله في هذه الحالة. — , , , .
, , . , SMT-. . , .
: « , , , , ».
, , . . , .
, . , , . , – , . ? , .

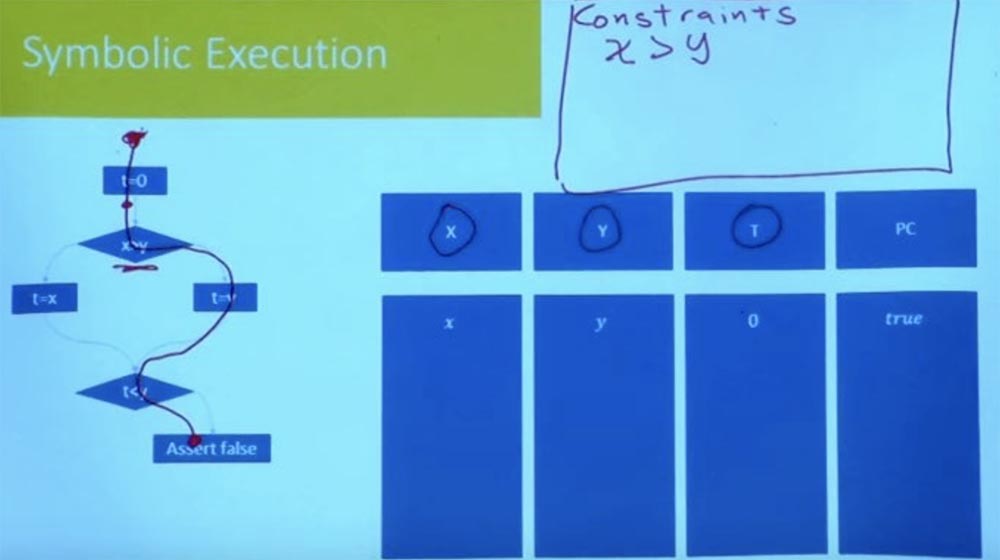
, , t=0 false.
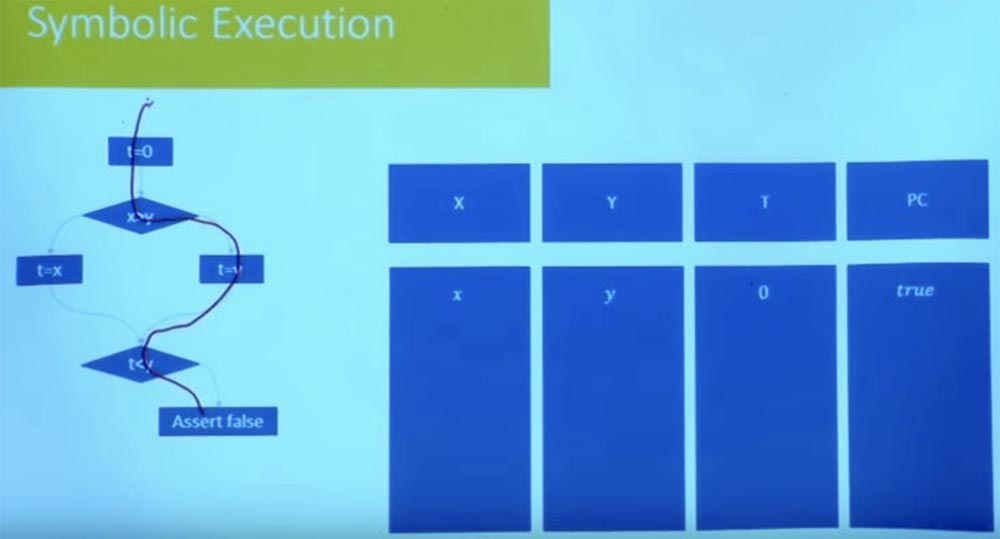
, , ? : , , .
, , , , , , .
, , t = 0, x, y 0. , . , , X , Y.
, X > Y.
55:00
دورة MIT "أمن أنظمة الكمبيوتر" المحاضرة 10: التنفيذ الرمزي ، الجزء 3النسخة الكاملة من الدورة متاحة
هنا .
شكرا لك على البقاء معنا. هل تحب مقالاتنا؟ هل تريد رؤية مواد أكثر إثارة للاهتمام؟ ادعمنا عن طريق تقديم طلب أو التوصية به لأصدقائك ،
خصم 30 ٪ لمستخدمي Habr على نظير فريد من خوادم مستوى الدخول التي اخترعناها لك: الحقيقة الكاملة حول VPS (KVM) E5-2650 v4 (6 نوى) 10GB DDR4 240GB SSD 1Gbps من 20 $ أو كيفية تقسيم الخادم؟ (تتوفر الخيارات مع RAID1 و RAID10 ، حتى 24 مركزًا وحتى 40 جيجابايت DDR4).
VPS (KVM) E5-2650 v4 (6 نوى) 10GB DDR4 240GB SSD 1Gbps حتى ديسمبر مجانًا عند الدفع لمدة ستة أشهر ، يمكنك الطلب
هنا .
ديل R730xd أرخص مرتين؟فقط لدينا 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV من 249 دولارًا في هولندا والولايات المتحدة! اقرأ عن
كيفية بناء مبنى البنية التحتية الطبقة باستخدام خوادم Dell R730xd E5-2650 v4 بتكلفة 9000 يورو مقابل سنت واحد؟