👨🏾‍🤝‍👨🏼 👩🏾‍🤝‍👩🏼 🤚🏾 نظرية اللعبة: صنع القرار مع أمثلة في Kotlin 👶🏼 🚏 📔

نظرية اللعبة هي نظام رياضي يفكر في نمذجة أفعال اللاعبين الذين لديهم هدف ، وهو اختيار الاستراتيجيات المثلى للسلوك في الصراع. لقد تم بالفعل تغطية هذا الموضوع في حبري ، لكننا سنتحدث اليوم عن بعض جوانبه بمزيد من التفصيل وننظر في أمثلة على Kotlin.

لذا ، فإن الاستراتيجية هي مجموعة من القواعد التي تحدد اختيار مسار العمل لكل خطوة شخصية ، اعتمادًا على الموقف. استراتيجية اللاعب الأمثل هي الاستراتيجية التي تضمن أفضل وضع في لعبة معينة ، أي أقصى ربح. إذا تم تكرار اللعبة عدة مرات واحتوت ، بالإضافة إلى التحركات العشوائية الشخصية ، فإن الإستراتيجية المثلى توفر الحد الأقصى لمتوسط الفوز.

مهمة نظرية اللعبة هي تحديد الاستراتيجيات المثلى للاعبين. الافتراض الرئيسي ، بناءً على الاستراتيجيات المثلى ، هو أن الخصم (أو الخصوم) ليس أقل ذكاءً من اللاعب نفسه ، ويقوم بكل شيء من أجل تحقيق هدفه. إن حساب الخصم المعقول هو واحد فقط من المواقف المحتملة في الصراع ، ولكن في نظرية الألعاب يتم وضعه في الأساس.

هناك ألعاب ذات طبيعة حيث يوجد مشارك واحد فقط يزيد من أرباحه. الألعاب ذات الطبيعة هي نماذج رياضية يعتمد فيها اختيار الحل على الواقع الموضوعي. على سبيل المثال ، طلب المستهلك ، حالة الطبيعة ، إلخ. "الطبيعة" هي مفهوم عام للخصم الذي لا يسعى إلى تحقيق أهدافه الخاصة. في هذه الحالة ، يتم استخدام عدة معايير لتحديد الاستراتيجية المثلى.
هناك نوعان من المهام في الألعاب ذات الطبيعة:

مهمة اتخاذ القرارات في ظروف الخطر عندما تكون الاحتمالات التي تقبل الطبيعة بها كل حالة ممكنة معروفة ؛
مهام صنع القرار في ظروف عدم اليقين ، عندما لا يكون من الممكن الحصول على معلومات حول احتمالات حدوث حالات الطبيعة.

باختصار يتم وصف هذه المعايير هنا .

الآن سنأخذ معايير اتخاذ القرار بعين الاعتبار في الاستراتيجيات البحتة ، وفي نهاية المقال سنحل اللعبة في استراتيجيات مختلطة بالطريقة التحليلية.

الحجز

أنا لست متخصصًا في نظرية اللعبة ، ولكن في هذا العمل استخدمت Kotlin للمرة الأولى. ومع ذلك ، قررت مشاركة نتائجي. إذا لاحظت أخطاء في المقالة أو كنت ترغب في تقديم المشورة ، يرجى PM.

بيان المشكلة

سنقوم بتحليل جميع معايير صنع القرار باستخدام المثال من خلال. المهمة هي: يحتاج المزارع إلى تحديد النسب لزرع حقله بثلاث محاصيل ، إذا كان محصول هذه المحاصيل ، وبالتالي الربح ، يعتمد على كيف سيكون الصيف: بارد وممطر ، عادي ، أو حار وجاف. قام المزارع بحساب صافي الربح من 1 هكتار من المحاصيل المختلفة اعتمادًا على الطقس. يتم تحديد اللعبة من خلال المصفوفة التالية:

علاوة على ذلك ، سنقدم هذه المصفوفة في شكل استراتيجيات:

، ، ، ، ، ، ، ،

$U_ {1} = (0،2،5) ، U_ {2} = (2،3،1) ، U_ {3} = (4،3، -1)$

يتم الإشارة إلى الاستراتيجية المثلى المطلوبة من قبل

$u_ {opt}$ . سوف نحل اللعبة باستخدام معايير والد والتفاؤل والتشاؤم و Savage و Hurwitz في ظروف عدم اليقين ومعايير Bayes و Laplace في ظروف الخطر.

كما ذكر أعلاه ، ستكون الأمثلة على Kotlin. ألاحظ أنه بشكل عام هناك حلول مثل Gambit (مكتوبة في C) ، و Axelrod و PyNFG (مكتوبة في Python) ، لكننا سنركب دراجتنا الخاصة ، مجمعة على الركبة ، فقط من أجل الوخز قليلاً أنيقة وعصرية و لغة برمجة الشباب.

لتنفيذ حل اللعبة برمجيًا ، سنقدم عدة فئات. أولاً ، نحتاج إلى فصل يسمح لنا بوصف صف أو عمود من مصفوفة اللعبة. الفئة بسيطة للغاية وتحتوي على قائمة بالقيم المحتملة (بدائل أو حالات الطبيعة) واسمها المقابل. سيتم استخدام المجال key لتحديد الهوية ، وكذلك للمقارنة ، وستكون هناك حاجة للمقارنة في تنفيذ الهيمنة.

صف أو عمود مصفوفة اللعبة

 import java.text.DecimalFormat import java.text.NumberFormat open class GameVector(name: String, values: List<Double>, key: Int = -1) : Comparable<GameVector> { val name: String val values: List<Double> val key: Int private val formatter:NumberFormat = DecimalFormat("#0.00") init { this.name = name; this.values = values; this.key = key; } public fun max(): Double? { return values.max(); } public fun min(): Double? { return values.min(); } override fun toString(): String{ return name + ": " + values .map { v -> formatter.format(v) } .reduce( {f1: String, f2: String -> "$f1 $f2"}) } override fun compareTo(other: GameVector): Int { var compare = 0 if (this.key == other.key){ return compare } var great = true for (i in 0..this.values.lastIndex){ great = great && this.values[i] >= other.values[i] } if (great){ compare = 1 }else{ var less = true for (i in 0..this.values.lastIndex){ less = less && this.values[i] <= other.values[i] } if (less){ compare = -1 } } return compare } }

تحتوي مصفوفة اللعبة على معلومات حول البدائل وحالات الطبيعة. بالإضافة إلى ذلك ، تنفذ بعض الطرق ، على سبيل المثال ، العثور على المجموعة المهيمنة والسعر الصافي للعبة.

مصفوفة اللعبة

 open class GameMatrix(matrix: List<List<Double>>, alternativeNames: List<String>, natureStateNames: List<String>) { val matrix: List<List<Double>> val alternativeNames: List<String> val natureStateNames: List<String> val alternatives: List<GameVector> val natureStates: List<GameVector> init { this.matrix = matrix; this.alternativeNames = alternativeNames this.natureStateNames = natureStateNames var alts: MutableList<GameVector> = mutableListOf() for (i in 0..matrix.lastIndex) { val currAlternative = alternativeNames[i] val gameVector = GameVector(currAlternative, matrix[i], i) alts.add(gameVector) } alternatives = alts.toList() var nss: MutableList<GameVector> = mutableListOf() val lastIndex = matrix[0].lastIndex //       ,     for (j in 0..lastIndex) { val currState = natureStateNames[j] var states: MutableList<Double> = mutableListOf() for (i in 0..matrix.lastIndex) { states.add(matrix[i][j]) } val gameVector = GameVector(currState, states.toList(), j) nss.add(gameVector) } natureStates = nss.toList() } open fun change (i : Int, j : Int, value : Double) : GameMatrix{ var mml = this.matrix.toMutableList() var rowi = mml[i].toMutableList() rowi.set(j, value) mml.set(i, rowi) return GameMatrix(mml.toList(), alternativeNames, natureStateNames) } open fun changeAlternativeName (i : Int, value : String) : GameMatrix{ var list = alternativeNames.toMutableList() list.set(i, value) return GameMatrix(matrix, list.toList(), natureStateNames) } open fun changeNatureStateName (j : Int, value : String) : GameMatrix{ var list = natureStateNames.toMutableList() list.set(j, value) return GameMatrix(matrix, alternativeNames, list.toList()) } fun size() : Pair<Int, Int>{ return Pair(alternatives.size, natureStates.size) } override fun toString(): String { return " :\n" + natureStateNames.reduce { n1: String, n2: String -> "$n1;\n$n2" } + "\n :\n" + alternatives .map { a: GameVector -> a.toString() } .reduce { a1: String, a2: String -> "$a1;\n$a2" } } protected fun dominateSet(gvl: List<GameVector>, list: MutableList<String>, dvv: Int) : MutableSet<GameVector>{ var dSet: MutableSet<GameVector> = mutableSetOf() for (gv in gvl){ for (gvv in gvl){ if (!dSet.contains(gv) && !dSet.contains(gvv)) { if (gv.compareTo(gvv) == dvv) { dSet.add(gv) list.add("[$gvv]  [$gv]") } } } } return dSet } open fun newMatrix(dCol: MutableSet<GameVector>, dRow: MutableSet<GameVector>) : GameMatrix{ var result: MutableList<MutableList<Double>> = mutableListOf() var ralternativeNames: MutableList<String> = mutableListOf() var rnatureStateNames: MutableList<String> = mutableListOf() val dIndex = dCol.map { c -> c.key }.toList() for (i in 0 .. natureStateNames.lastIndex){ if (!dIndex.contains(i)){ rnatureStateNames.add(natureStateNames[i]) } } for (gv in this.alternatives){ if (!dRow.contains(gv)){ var nr: MutableList<Double> = mutableListOf() for (i in 0 .. gv.values.lastIndex){ if (!dIndex.contains(i)){ nr.add(gv.values[i]) } } result.add(nr) ralternativeNames.add(gv.name) } } val rlist = result.map { r -> r.toList() }.toList() return GameMatrix(rlist, ralternativeNames.toList(), rnatureStateNames.toList()) } fun dominateMatrix(): Pair<GameMatrix, List<String>>{ var list: MutableList<String> = mutableListOf() var dCol: MutableSet<GameVector> = dominateSet(this.natureStates, list, 1) var dRow: MutableSet<GameVector> = dominateSet(this.alternatives, list, -1) val newMatrix = newMatrix(dCol, dRow) var ddgm = Pair(newMatrix, list.toList()) val ret = iterate(ddgm, list) return ret; } protected fun iterate(ddgm: Pair<GameMatrix, List<String>>, list: MutableList<String>) : Pair<GameMatrix, List<String>>{ var dgm = this var lddgm = ddgm while (dgm.size() != lddgm.first.size()){ dgm = lddgm.first list.addAll(lddgm.second) lddgm = dgm.dominateMatrix() } return Pair(dgm,list.toList().distinct()) } fun minClearPrice(): Double{ val map: List<Double> = this.alternatives.map { a -> a?.min() ?: 0.0 } return map?.max() ?: 0.0 } fun maxClearPrice(): Double{ val map: List<Double> = this.natureStates.map { a -> a?.max() ?: 0.0 } return map?.min() ?: 0.0 } fun existsClearStrategy() : Boolean{ return minClearPrice() >= maxClearPrice() } }

نحن نصف الواجهة التي تلبي المعايير

المعيار

 interface ICriteria { fun optimum(): List<GameVector> }

صنع القرار في ظل عدم اليقين

يشير اتخاذ القرارات في مواجهة عدم اليقين إلى أن اللاعب لا يعارضه خصم معقول.

معيار والد

يضاعف معيار والد أسوأ نتيجة ممكنة:

$u_ {opt} = max_ {i} min_ {j} [U]$

يؤمن استخدام المعيار ضد أسوأ النتائج ، ولكن ثمن هذه الاستراتيجية هو فقدان الفرصة للحصول على أفضل نتيجة ممكنة.

تأمل في مثال. للاستراتيجيات

، ، ، ، ، ، ، ،

$U_ {1} = (0،2،5) ، U_ {2} = (2،3،1) ، U_ {3} = (4،3، -1)$ أوجد أدنى المستويات واحصل على الثلاثة التالية

، ،

$S = (0 ، 1 ، -1)$ . الحد الأقصى للثلاثية المشار إليها سيكون القيمة 1 ، وبالتالي ، وفقًا لمعيار والد ، فإن استراتيجية الفوز هي الاستراتيجية

، ،

$U_ {2} = (2،3،1)$ الموافق لثقافة الزراعة 2.

تطبيق البرنامج لمعيار والد بسيط:

 class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } }

من أجل الوضوح ، سأظهر لأول مرة كيف سيبدو الحل كاختبار:

اختبر

 private fun matrix(): GameMatrix { val alternativeNames: List<String> = listOf(" 1", " 2", " 3") val natureStateNames: List<String> = listOf("  ", "", "  ") val matrix: List<List<Double>> = listOf( listOf(0.0, 2.0, 5.0), listOf(2.0, 3.0, 1.0), listOf(4.0, 3.0, -1.0) ) val gm = GameMatrix(matrix, alternativeNames, natureStateNames) return gm; } } private fun testCriteria(gameMatrix: GameMatrix, criteria: ICriteria, name: String){ println(gameMatrix.toString()) val optimum = criteria.optimum() println("$name.  : ") optimum.forEach { o -> println(o.toString()) } } @Test fun testWaldCriteria() { val matrix = matrix(); val criteria = WaldCriteria(matrix) testCriteria(matrix, criteria, " ") }

من السهل تخمين أنه بالنسبة لمعايير أخرى ، سيكون الفرق فقط في إنشاء كائن criteria .

معيار التفاؤل

عند استخدام معيار المتفائل ، يختار اللاعب حلاً يعطي أفضل نتيجة ، في حين يفترض المتفائل أن ظروف اللعبة ستكون الأكثر ملاءمة له:

$u_ {opt} = max_ {i} max_ {j} [U]$

يمكن أن تؤدي استراتيجية المتفائل إلى عواقب سلبية عندما يتزامن الحد الأقصى للعرض مع الحد الأدنى للطلب - قد تتلقى الشركة خسائر عند شطب المنتجات غير المباعة. في نفس الوقت ، فإن استراتيجية المتفائل لها معنى معين ، على سبيل المثال ، لا تحتاج لرعاية العملاء غير الراضين ، حيث يتم تلبية أي طلب محتمل دائمًا ، لذلك لا توجد حاجة للحفاظ على موقع العملاء. إذا تم تحقيق الحد الأقصى للطلب ، فإن استراتيجية المتفائل تسمح لك بالحصول على أقصى فائدة بينما ستؤدي الاستراتيجيات الأخرى إلى خسارة الأرباح. هذا يعطي مزايا تنافسية معينة.

تأمل في مثال. للاستراتيجيات

$U_ {1} = (0،2،5) ، U_ {2} = (2،3،1) ، U_ {3} = (4،3، -1)$ تجد ، تجد الحد الأقصى والحصول على الثلاثة التالية

$S = (5 ، 3 ، 4)$ . الحد الأقصى للثلاثية المشار إليها سيكون القيمة 5 ، وبالتالي ، وفقًا لمعيار التفاؤل ، فإن استراتيجية الفوز هي الاستراتيجية

$U_ {1} = (0.2.5)$ الموافق لثقافة الزراعة 1.

لا يختلف تطبيق معيار التفاؤل تقريبًا عن معيار والد:

 class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } }

معيار التشاؤم

الغرض من هذا المعيار هو تحديد أصغر عنصر في مصفوفة اللعبة من الحد الأدنى للعناصر الممكنة:

$u_ {opt} = min_ {i} min_ {j} [U]$

يشير معيار التشاؤم إلى أن تطوير الأحداث سيكون غير موات لصانع القرار. عند استخدام هذا المعيار ، يسترشد صانع القرار بالخسارة المحتملة للسيطرة على الموقف ، لذلك يحاول استبعاد المخاطر المحتملة عن طريق اختيار الخيار بأقل ربحية.

تأمل في مثال. للاستراتيجيات

$U_ {1} = (0،2،5) ، U_ {2} = (2،3،1) ، U_ {3} = (4،3، -1)$ تجد ، تجد الحد الأدنى والحصول على الثلاثة التالية

$S = (0 ، 1 ، -1)$ . الحد الأدنى للثلاثية المشار إليها سيكون القيمة -1 ، وبالتالي ، وفقًا لمعيار التشاؤم ، فإن استراتيجية الفوز هي الاستراتيجية

$U_ {3} = (4.3، -1)$ الموافق لثقافة الزراعة 3.

بعد التعرف على معايير والد والتفاؤل ، من السهل تخمين كيف ستبدو فئة معيار التشاؤم:

 class PessimismCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val min = mins.minWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == min!!.second } .map { m -> m.first } } }

معيار الهمج

يتضمن معيار سافاج (معيار المتشائم المتشائم) التقليل إلى أقصى حد من الأرباح الضائعة ، وبعبارة أخرى ، يتم تقليل الأسف الأكبر للأرباح المفقودة:

$u_ {opt} = min_ {i} max_ {j} [S] \\ s_ {i، j} = (max \ start {bmatrix} u_ {1، j} \\ u_ {2، j} \\. .. \\ u_ {n، j} \ end {bmatrix} - u_ {i، j})$

في هذه الحالة ، S هي مصفوفة الندم.

يجب أن يعطي الحل الأمثل وفقًا لمعيار سافاج أقل الأسف من الندم الموجود في الخطوة السابقة. الحل المطابق للأداة المساعدة الموجودة سيكون الأمثل.

تتضمن ميزات الحل الذي تم الحصول عليه غيابًا مضمونًا لأكبر خيبات الأمل وانخفاضًا مضمونًا في أقصى انتصارات ممكنة للاعبين الآخرين.

تأمل في مثال. للاستراتيجيات

$U_ {1} = (0،2،5) ، U_ {2} = (2،3،1) ، U_ {3} = (4،3، -1)$ جعل مصفوفة الندم:

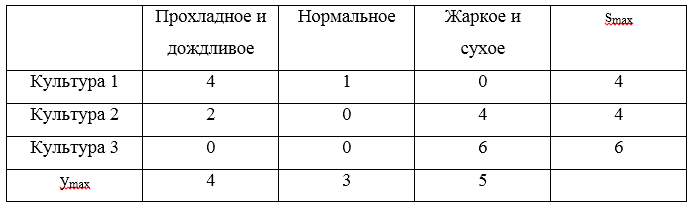
ثلاث ندم كحد أقصى

$S = (4،4،6)$ . ستكون القيمة الدنيا لهذه المخاطر قيمة 4 ، والتي تتوافق مع الاستراتيجيات

$U_ {1}$ و

$U_ {2}$ .

برمجة اختبار سافاج أكثر صعوبة بقليل:

 class SavageCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.risk(): List<Pair<GameVector, Double?>> { val maxStates = this.natureStates.map { n -> Pair(n, n.values.max()) } .map { n -> n.first.key to n.second }.toMap() var am: MutableList<Pair<GameVector, List<Double>>> = mutableListOf() for (a in this.alternatives) { var v: MutableList<Double> = mutableListOf() for (i in 0..a.values.lastIndex) { val mn = maxStates.get(i) v.add(mn!! - a.values[i]) } am.add(Pair(a, v.toList())) } return am.map { m -> Pair(m.first, m.second.max()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.risk() val minRisk = risk.minWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == minRisk!!.second } .map { m -> m.first } } }

معيار Hurwitz

معيار هورويتز هو حل وسط منظم بين التشاؤم الشديد والتفاؤل التام:

$u_ {opt} = max (\ gamma × A (k) + A (0) × (1 - \ gamma))$

أ (0) هي استراتيجية المتشائم المتطرف ، أ (ك) هي استراتيجية المتفائل الكامل ،

$\ gamma = 1$ - القيمة المحددة لمعامل الوزن:

$0 \ leq \ gamma \ leq1$ ؛

$\ gamma = 0$ - التشاؤم الشديد

$\ gamma = 1$ - التفاؤل الكامل.

مع عدد قليل من الاستراتيجيات المنفصلة ، تحديد القيمة المطلوبة لمعامل الوزن

$\ gamma$ ، ثم قم بتقريب النتيجة إلى أقرب قيمة ممكنة ، مع الأخذ في الاعتبار التقدير المنجز.

تأمل في مثال. للاستراتيجيات

$U_ {1} = (0،2،5) ، U_ {2} = (2،3،1) ، U_ {3} = (4،3، -1)$ . نفترض أن معامل التفاؤل

$\ gamma = $ 0.$ . الآن اصنع طاولة:

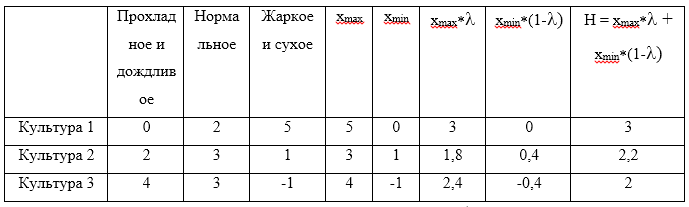
ستكون القيمة القصوى من H المحسوبة هي القيمة 3 ، والتي تتوافق مع الاستراتيجية

$U_ {1}$ .

إن تنفيذ معيار Hurwitz هو بالفعل أكبر حجمًا:

 class HurwitzCriteria(gameMatrix: GameMatrix, optimisticKoef: Double) : ICriteria { val gameMatrix: GameMatrix val optimisticKoef: Double init { this.gameMatrix = gameMatrix this.optimisticKoef = optimisticKoef } inner class HurwitzParam(xmax: Double, xmin: Double, optXmax: Double){ val xmax: Double val xmin: Double val optXmax: Double val value: Double init{ this.xmax = xmax this.xmin = xmin this.optXmax = optXmax value = xmax * optXmax + xmin * (1 - optXmax) } } fun GameMatrix.getHurwitzParams(): List<Pair<GameVector, HurwitzParam>> { return this.alternatives.map { a -> Pair(a, HurwitzParam(a.max()!!, a.min()!!, optimisticKoef)) } } override fun optimum(): List<GameVector> { val hpar = gameMatrix.getHurwitzParams() val maxHurw = hpar.maxWith(Comparator { o1, o2 -> o1.second.value.compareTo(o2.second.value) }) return hpar .filter { r -> r.second == maxHurw!!.second } .map { m -> m.first } } }

صنع القرار في خطر

يمكن أن تعتمد طرق اتخاذ القرار على معايير اتخاذ القرار في ظروف الخطر ، مع مراعاة الشروط التالية:

نقص المعلومات الموثوقة حول العواقب المحتملة ؛
وجود توزيعات احتمالية ؛
معرفة احتمالية النتائج أو العواقب لكل قرار.

إذا تم اتخاذ قرار في ظل ظروف الخطر ، يتم وصف تكاليف القرارات البديلة من خلال التوزيعات الاحتمالية. في هذا الصدد ، يعتمد القرار على استخدام معيار القيمة المتوقعة ، والذي يتم بموجبه مقارنة الحلول البديلة من حيث تعظيم الأرباح المتوقعة أو تقليل التكاليف المتوقعة.

يمكن تخفيض معيار القيمة المتوقعة إما لتعظيم الربح (المتوسط) المتوقع ، أو لتقليل التكاليف المتوقعة. في هذه الحالة ، يُفترض أن الربح (التكاليف) المرتبط بكل حل بديل هو متغير عشوائي.

عادة ما تكون صياغة مثل هذه المهام على النحو التالي: يختار الشخص أي إجراء في موقف تؤثر فيه الأحداث العشوائية على نتيجة الإجراء. لكن اللاعب لديه بعض المعرفة حول احتمالات هذه الأحداث ويمكنه حساب التركيبة الأكثر ربحية وتسلسل أفعاله.

من أجل الاستمرار في إعطاء أمثلة ، نكمل مصفوفة اللعبة باحتمالات:

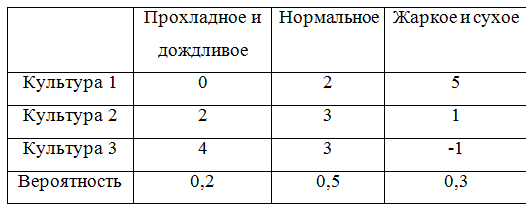
من أجل مراعاة الاحتمالات ، يجب إعادة تصميم فصل يصف مصفوفة اللعبة قليلاً. اتضح ، في الواقع ، ليس أنيقًا جدًا ، ولكن حسنًا.

مصفوفة اللعبة مع الاحتمالات

 open class ProbabilityGameMatrix(matrix: List<List<Double>>, alternativeNames: List<String>, natureStateNames: List<String>, probabilities: List<Double>) : GameMatrix(matrix, alternativeNames, natureStateNames) { val probabilities: List<Double> init { this.probabilities = probabilities; } override fun change (i : Int, j : Int, value : Double) : GameMatrix{ val cm = super.change(i, j, value) return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities) } override fun changeAlternativeName (i : Int, value : String) : GameMatrix{ val cm = super.changeAlternativeName(i, value) return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities) } override fun changeNatureStateName (j : Int, value : String) : GameMatrix{ val cm = super.changeNatureStateName(j, value) return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities) } fun changeProbability (j : Int, value : Double) : GameMatrix{ var list = probabilities.toMutableList() list.set(j, value) return ProbabilityGameMatrix(matrix, alternativeNames, natureStateNames, list.toList()) } override fun toString(): String { var s = "" val formatter: NumberFormat = DecimalFormat("#0.00") for (i in 0 .. natureStateNames.lastIndex){ s += natureStateNames[i] + " = " + formatter.format(probabilities[i]) + "\n" } return " :\n" + s + " :\n" + alternatives .map { a: GameVector -> a.toString() } .reduce { a1: String, a2: String -> "$a1;\n$a2" } } override fun newMatrix(dCol: MutableSet<GameVector>, dRow: MutableSet<GameVector>) : GameMatrix{ var result: MutableList<MutableList<Double>> = mutableListOf() var ralternativeNames: MutableList<String> = mutableListOf() var rnatureStateNames: MutableList<String> = mutableListOf() var rprobailities: MutableList<Double> = mutableListOf() val dIndex = dCol.map { c -> c.key }.toList() for (i in 0 .. natureStateNames.lastIndex){ if (!dIndex.contains(i)){ rnatureStateNames.add(natureStateNames[i]) } } for (i in 0 .. probabilities.lastIndex){ if (!dIndex.contains(i)){ rprobailities.add(probabilities[i]) } } for (gv in this.alternatives){ if (!dRow.contains(gv)){ var nr: MutableList<Double> = mutableListOf() for (i in 0 .. gv.values.lastIndex){ if (!dIndex.contains(i)){ nr.add(gv.values[i]) } } result.add(nr) ralternativeNames.add(gv.name) } } val rlist = result.map { r -> r.toList() }.toList() return ProbabilityGameMatrix(rlist, ralternativeNames.toList(), rnatureStateNames.toList(), rprobailities.toList()) } } }

معيار بايز

يستخدم معيار بايز (معيار التوقع) في مشاكل صنع القرار في ظروف الخطر كتقييم للاستراتيجية

$u_ {i}$ يظهر التوقع الرياضي للمتغير العشوائي المقابل. وفقا لهذه القاعدة ، استراتيجية اللاعب الأمثل

$u_ {opt}$ تم العثور عليها من الحالة:

$u_ {opt} = max_ {1 \ leq i \ leq n} M (u_ {i}) \\ M (u_ {i}) = max_ {1 \ leq i \ leq n} \ sum_ {j = 1} ^ m u_ {i، j} \ cdot y_ {j} ^ 0$

بمعنى آخر ، مؤشر عدم كفاءة الإستراتيجية

$u_ {i}$ بمعيار بايز فيما يتعلق بالمخاطر هو متوسط القيمة (التوقع) لمخاطر الصف الأول من المصفوفة

$U$ الذي تتزامن احتمالاته مع احتمالات الطبيعة. ثم الإستراتيجية المثلى بين الاستراتيجيات البحتة لمعيار بايز فيما يتعلق بالمخاطر هي الاستراتيجية

$u_ {opt}$ مع الحد الأدنى من عدم الكفاءة ، أي الحد الأدنى من المخاطر. المعيار البايزي معادل فيما يتعلق بالأرباح والمرتبطة بالمخاطر ، أي إذا كانت الاستراتيجية

$u_ {opt}$ هو الأمثل وفقًا لمعيار Bayes فيما يتعلق بالربح ، ثم هو الأمثل وفقًا لمعيار Bayes فيما يتعلق بالمخاطر ، والعكس صحيح.

دعنا ننتقل إلى المثال ونحسب التوقعات الرياضية:

$M_1 = 0 \ cdot0.2 +2 \ cdot0.5 +5 \ cdot0.3 = 2.5 ؛ \\ M_2 = 2 \ cdot0.2 +3 \ cdot0.5 +1 \ cdot0.3 = 2.2 ؛ \\ M_4 = 0 \ cdot0.2 +3 \ cdot0.5 + (- 1) \ cdot0.3 = 2.0؛$

الحد الأقصى للتوقعات الرياضية هو

$M_1$ لذلك ، فإن استراتيجية الفوز هي استراتيجية

$U_1$ .

تطبيق البرمجيات لمعيار بايز:

 class BayesCriteria(gameMatrix: ProbabilityGameMatrix) : ICriteria { val gameMatrix: ProbabilityGameMatrix init { this.gameMatrix = gameMatrix } fun ProbabilityGameMatrix.bayesProbability(): List<Pair<GameVector, Double?>> { var am: MutableList<Pair<GameVector, Double>> = mutableListOf() for (a in this.alternatives) { var alprob: Double = 0.0 for (i in 0..a.values.lastIndex) { alprob += a.values[i] * this.probabilities[i] } am.add(Pair(a, alprob)) } return am.toList(); } override fun optimum(): List<GameVector> { val risk = gameMatrix.bayesProbability() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } }

معيار لابلاس

يقدم معيار لابلاس زيادة مبسطة للتوقعات الرياضية للفائدة عندما يكون افتراض الاحتمال المتساوي لمستويات الطلب صحيحًا ، مما يلغي الحاجة إلى جمع إحصائيات حقيقية.

بشكل عام ، عند استخدام معيار لابلاس ، يتم تحديد مصفوفة المرافق المتوقعة والمعيار الأمثل على النحو التالي:

$u_ {opt} = max [\ overline {U}] \\ \ overline {U} = \ start {bmatrix} \ overline {u} _ {1} \\ \ overline {u} _ {2} \\. .. \\ \ overline {u} _ {n} \ end {bmatrix} ، \ overline {u} _ {i} = \ frac {1} {n} \ sum_ {j = 1} ^ nu_ {i، j }$

لنأخذ مثال صنع القرار بمعيار لابلاس. نحسب المتوسط الحسابي لكل استراتيجية:

$\ overline {u} _ {1} = \ frac {1} {3} \ cdot (0 + 2 + 5) = 2.3 \\ \ overline {u} _ {2} = \ frac {1} { 3} \ cdot (2 + 3 + 1) = 2.0 \\ \ overline {u} _ {3} = \ frac {1} {3} \ cdot (4 + 3-1) = 2.0 دولا$

لذا فإن الإستراتيجية الفائزة هي الإستراتيجية

$U_1$ .

تطبيق برمجيات معيار لابلاس:

 class LaplaceCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.arithemicMean(): List<Pair<GameVector, Double>> { return this.alternatives.map { m -> Pair(m, m.values.average()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.arithemicMean() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second.compareTo(o2.second) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } }

استراتيجيات مختلطة. طريقة تحليلية

تسمح لك الطريقة التحليلية بحل اللعبة باستراتيجيات مختلطة. من أجل صياغة خوارزمية لإيجاد حل للعبة بطريقة تحليلية ، نعتبر بعض المفاهيم الإضافية.

إستراتيجية

استراتيجية يهيمن عليها

$U_{i}$

، إن وجدت

$U_{i-1}$

$u_{1..n} \in U_{i} \geq u_{1..n} \in U_{i-1}$ .بمعنى آخر ، إذا كانت جميع العناصر في صف من مصفوفة الدفع أكبر من العناصر المقابلة في صف آخر أو مساوية لها ، فإن الصف الأول يهيمن على الصف الثاني ويسمى الصف المهيمن. وأيضًا إذا كانت جميع العناصر في أحد أعمدة مصفوفة الدفع أقل أو تساوي العناصر المقابلة في عمود آخر ، فإن العمود الأول يهيمن على العمود الثاني ويسمى العمود المهيمن.

يسمى أدنى سعر للعبة

$\alpha = max_i min_j u_{ij}$ .
يسمى السعر الأعلى للعبة

$\beta = min_j max_i u_{ij}$ .

الآن يمكنك صياغة خوارزمية لحل اللعبة بالطريقة التحليلية:

احسب القاع والعلوي $\alpha$ لعبة الأسعار. إذا $\beta$ ، ثم اكتب الإجابة في إستراتيجيات محضة ؛ إذا لم يكن كذلك ، فتابع الحل بشكل أكبر $\alpha = \beta$
حذف الصفوف السائدة من الأعمدة السائدة. قد يكون هناك العديد. في مكانها في الاستراتيجية المثلى ، ستكون المكونات المقابلة 0
حل لعبة المصفوفة عن طريق البرمجة الخطية.

لإعطاء مثال ، تحتاج إلى إعطاء فئة تصف الحل

حل

 class Solve(gamePriceObr: Double, solutions: List<Double>, names: List<String>) { val gamePrice: Double val gamePriceObr: Double val solutions: List<Double> val names: List<String> private val formatter: NumberFormat = DecimalFormat("#0.00") init{ this.gamePrice = 1 / gamePriceObr this.gamePriceObr = gamePriceObr; this.solutions = solutions this.names = names } override fun toString(): String{ var s = " : " + formatter.format(gamePrice) + "\n" for (i in 0..solutions.lastIndex){ s += "$i) " + names[i] + " = " + formatter.format(solutions[i] / gamePriceObr) + "\n" } return s } fun itersect(matrix: GameMatrix): String{ var s = " : " + formatter.format(gamePrice) + "\n" for (j in 0..matrix.alternativeNames.lastIndex) { var f = false val a = matrix.alternativeNames[j] for (i in 0..solutions.lastIndex) { if (a.equals(names[i])) { s += "$j) " + names[i] + " = " + formatter.format(solutions[i] / gamePriceObr) + "\n" f = true break } } if (!f){ s += "$j) " + a + " = 0\n" } } return s } }

والفئة التي تنفذ الحل بطريقة البسيط. نظرًا لأنني لا أفهم الرياضيات ، فقد استخدمت التنفيذ الجاهز من Apache Commons Math

حلالا

 open class Solver (gameMatrix: GameMatrix) { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } fun solve(): Solve{ val goalf: List<Double> = gameMatrix.alternatives.map { a -> 1.0 } val f = LinearObjectiveFunction(goalf.toDoubleArray(), 0.0) val constraints = ArrayList<LinearConstraint>() for (alt in gameMatrix.alternatives){ constraints.add(LinearConstraint(alt.values.toDoubleArray(), Relationship.LEQ, 1.0)) } val solution = SimplexSolver().optimize(f, LinearConstraintSet(constraints), GoalType.MAXIMIZE, NonNegativeConstraint(true)) val sl: List<Double> = solution.getPoint().toList() val solve = Solve(solution.getValue(), sl, gameMatrix.alternativeNames) return solve } }

الآن نقوم بتنفيذ الحل بالطريقة التحليلية. للتوضيح ، نأخذ مصفوفة لعبة أخرى:

$\begin{pmatrix} 2& 4& 8& 5 \\ 6& 2& 4& 6\\ 3& 2& 5& 4 \end{pmatrix}$

هناك مجموعة مهيمنة في هذه المصفوفة:

$\begin{pmatrix} 2& 4\\ 6& 2\end{pmatrix}$

الحل

 val alternativeNames: List<String> = listOf(" 1", " 2", " 3") val natureStateNames: List<String> = listOf("  ", "", "  ", "") val matrix: List<List<Double>> = listOf( listOf(2.0, 4.0, 8.0, 5.0), listOf(6.0, 2.0, 4.0, 6.0), listOf(3.0, 2.0, 5.0, 4.0) ) val gm = GameMatrix(matrix, alternativeNames, natureStateNames) val (dgm, list) = gm.dominateMatrix() println(dgm.toString()) println(list.reduce({s1, s2 -> s1 + "\n" + s2})) println() val s: Solver = Solver(dgm) val solve = s.solve() println(solve)

حل اللعبة

مع سعر اللعبة يساوي 3.33

$(0,33; 0,67; 0)$

بدلا من الاستنتاج

آمل أن تكون هذه المقالة مفيدة لأولئك الذين يحتاجون لتقريب أول مع حل الألعاب مع الطبيعة. بدلاً من الاستنتاجات ، رابط إلى GitHub .

سأكون ممتنا لردود الفعل البناءة!

نظرية اللعبة: صنع القرار مع أمثلة في Kotlin