مرحبا يا هبر! أقدم لكم الصفحة الأولى من حل اللصوص متعدد الأسلحة: مقارنة بين إبسيلون-الجشع وأخذ عينات طومسون .

مشكلة ماكينات الألعاب المتعددة

تعد مشكلة قطاع ماكينات الألعاب المتعددة من المهام الأساسية في علم الحلول. وهي مشكلة التخصيص الأمثل للموارد في ظل ظروف عدم اليقين. جاء اسم "ماكينات الألعاب المتعددة" نفسها من ماكينات القمار القديمة التي تسيطر عليها المقابض. كانت هذه البنادق الهجومية تُلقب بـ "قطاع الطرق" ، لأنه بعد التحدث معهم ، عادة ما يشعر الناس بالسرقة. تخيل الآن أن هناك العديد من هذه الآلات وفرصة الفوز على سيارات مختلفة مختلفة. نظرًا لأننا بدأنا اللعب بهذه الأجهزة ، فإننا نرغب في تحديد الفرصة الأكبر واستخدام هذا الجهاز أكثر من غيرها.

تكمن المشكلة في هذا: كيف نفهم بشكل أكثر فاعلية أي جهاز هو الأنسب ، وفي نفس الوقت نجرب العديد من الميزات في الوقت الحقيقي؟ هذه ليست نوعًا من المشكلة النظرية ، إنها مشكلة يواجهها العمل طوال الوقت. على سبيل المثال ، لدى الشركة العديد من الخيارات للرسائل التي يجب عرضها للمستخدمين (على سبيل المثال ، تتضمن الرسائل إعلانات ومواقع وصور) بحيث تزيد الرسائل المحددة من مهمة تجارية معينة (التحويل ، إمكانية النقر ، إلخ.)

الطريقة النموذجية لحل هذه المشكلة هي تشغيل اختبارات A / B عدة مرات. أي لعدة أسابيع لإظهار كل خيار بشكل متساوٍ ، ثم ، بناءً على الاختبارات الإحصائية ، حدد الخيار الأفضل. هذه الطريقة مناسبة عندما يكون هناك عدد قليل من الخيارات ، على سبيل المثال ، 2 أو 4. ولكن عندما يكون هناك العديد من الخيارات ، يصبح هذا النهج غير فعال - في الوقت الضائع والأرباح الضائعة.

يجب أن يكون من السهل فهم من أين يأتي الوقت الضائع. المزيد من الخيارات - هناك حاجة إلى المزيد من اختبارات A / B - هناك حاجة إلى مزيد من الوقت لاتخاذ القرار. إن حدوث خسارة في الأرباح ليس واضحا. ضياع الفرصة (تكلفة الفرصة) - التكاليف المرتبطة بحقيقة أننا بدلاً من إجراء واحد قمنا بعمل آخر ، أي ببساطة ، هذا ما فقدناه بالاستثمار في A بدلاً من B. الاستثمار في B هو الربح الضائع من الاستثمار في A. نفس الشيء مع فحص الخيار. لا ينبغي مقاطعة اختبارات A / B حتى الانتهاء. هذا يعني أن المجرب لا يعرف الخيار الأفضل حتى انتهاء الاختبار. ومع ذلك ، لا يزال يعتقد أن أحد الخيارات سيكون أفضل من الآخر. وهذا يعني أنه من خلال إطالة اختبارات A / B ، فإننا لا نظهر أفضل الخيارات لعدد كبير بما فيه الكفاية من الزائرين (على الرغم من أننا لا نعرف أي الخيارات ليست الأفضل) ، وبالتالي نفقد أرباحنا. هذه هي الفائدة المفقودة من اختبار A / B. إذا كان هناك اختبار A / B واحد فقط ، فربما يكون الربح الضائع ليس كبيرًا على الإطلاق. يعني عدد كبير من اختبارات A / B أنه لفترة طويلة علينا أن نظهر للعملاء الكثير من الخيارات ليست الأفضل. سيكون من الأفضل إذا استطعت التخلص من الخيارات السيئة بسرعة في الوقت الفعلي ، وعندها فقط ، عندما يكون هناك القليل من الخيارات المتبقية ، استخدم اختبارات A / B لها.

العينات أو الوكلاء هي طرق لاختبار توزيع الخيارات وتحسينه بسرعة. في هذه المقالة ، سوف أقدمك إلى أخذ عينات طومسون وخصائصه. سأقوم أيضًا بمقارنة أخذ عينات طومسون مع خوارزمية إبسيلون-الجشع ، وهو خيار شائع آخر لمشكلة قطاع ماكينات الألعاب المتعددة. سيتم تنفيذ كل شيء في بايثون من الصفر - يمكن العثور على جميع التعليمات البرمجية هنا .

قاموس موجز للمفاهيم

• Agent، sampler، bandit ( agent، sampler، bandit ) - خوارزمية تتخذ قرارات بشأن الخيار الذي تظهر.
• متغير - صيغة مختلفة للرسالة التي يراها الزائر.
• الإجراء - الإجراء الذي اختارته الخوارزمية (أي خيار لإظهاره).
• استخدم ( استغلال ) - قم بالاختيار لتعظيم المكافأة الإجمالية بناءً على البيانات المتاحة.
• استكشف ، استكشف - قم بعمل خيارات لفهم أفضل لاسترداد كل خيار.
• الجائزة ، النقاط ( الدرجة ، المكافأة ) - مهمة عمل ، على سبيل المثال ، التحويل أو إمكانية النقر. من أجل البساطة ، نعتقد أنه يتم توزيعه ذي الحدين ويساوي 1 أو 0 - يتم النقر عليه أم لا.
• البيئة - السياق الذي يعمل فيه الوكيل - الخيارات و "الاسترداد" المخفي للمستخدم.
• الاسترداد ، احتمال النجاح ( معدل العائد ) - متغير مخفي يساوي احتمال الحصول على درجة = 1 ، لكل خيار مختلف. لكن المستخدم لا يراها.
• حاول ( تجريبي ) - يزور المستخدم الصفحة.
• الأسف هو الفرق بين ما سيكون أفضل نتيجة لجميع الخيارات المتاحة وما هو نتيجة الخيار المتاح في المحاولة الحالية. وكلما قل الندم على الإجراءات المتخذة ، كان ذلك أفضل.
• الرسالة ( الرسالة ) - بانر وخيار الصفحة والمزيد ، إصدارات مختلفة نريد تجربتها.
• أخذ العينات - توليد عينة من توزيع معين.

استكشاف واستغلال

الوكلاء هم خوارزميات تبحث عن نهج لاتخاذ القرار في الوقت الفعلي من أجل تحقيق التوازن بين استكشاف مساحة الخيارات واستخدام الخيار الأفضل. هذا التوازن مهم جدا. يجب التحقق من مساحة الخيارات من أجل الحصول على فكرة عن الخيار الأفضل. إذا اكتشفنا لأول مرة هذا الخيار الأمثل ، ثم استخدمناه طوال الوقت ، فسنضاعف إجمالي المكافأة المتاحة لنا من البيئة. من ناحية أخرى ، نريد أيضًا استكشاف خيارات أخرى ممكنة - ماذا لو تبين أنها ستكون أفضل في المستقبل ، لكننا لا نعرف حتى الآن؟ بعبارة أخرى ، نريد أن نضمن ضد الخسائر المحتملة ، محاولين تجربة القليل من الخيارات دون المستوى الأمثل من أجل توضيح تعويضاتهم بأنفسهم. إذا كان عائدهم أعلى بالفعل ، فيمكن إظهارهم في كثير من الأحيان. ميزة أخرى من استكشاف الخيارات هي أنه يمكننا أن نفهم بشكل أفضل ليس فقط متوسط ​​العائد ، ولكن أيضًا كيف يتم توزيع العائد تقريبًا ، أي يمكننا تقدير عدم اليقين بشكل أفضل.
وبالتالي ، فإن المشكلة الرئيسية هي الحل - ما هي أفضل طريقة للخروج من المأزق بين الاستكشاف والاستغلال (الاستكشاف - الاستغلال).

خوارزمية إبسيلون الجشع

الطريقة النموذجية للخروج من هذه المعضلة هي خوارزمية إبسيلون الجشع. "الجشع" يعني بالضبط ما كنت تعتقد. بعد بعض الفترة الأولية ، عندما نجري محاولات عن طريق الخطأ - لنفترض 1000 مرة ، تختار الخوارزمية بفارغ الصبر الخيار الأفضل في النسبة المئوية للمحاولات. على سبيل المثال ، إذا كان e = 0.05 ، فإن الخوارزمية 95٪ من الوقت تحدد الخيار الأفضل ، وفي 5٪ المتبقية من الوقت تقوم بتحديد محاولات عشوائية. في الواقع ، هذه خوارزمية فعالة إلى حد ما ، ومع ذلك ، قد لا تكون كافية لاستكشاف مساحة الخيارات ، وبالتالي ، لن تكون جيدة بما يكفي لتقييم الخيار الأفضل ، لتعلق في خيار دون المستوى الأمثل. دعونا نوضح في الكيفية كيف تعمل هذه الخوارزمية.

لكن أولاً ، بعض التبعيات. يجب أن نحدد البيئة. هذا هو السياق الذي ستعمل فيه الخوارزميات. في هذه الحالة ، السياق بسيط للغاية. يتصل بالوكيل بحيث يقرر الوكيل الإجراء الذي يجب اختياره ، ثم يبدأ السياق هذا الإجراء ويعيد النقاط المستلمة له إلى الوكيل (الذي يقوم بتحديث حالته بطريقة أو بأخرى).

class Environment: def __init__(self, variants, payouts, n_trials, variance=False): self.variants = variants if variance: self.payouts = np.clip(payouts + np.random.normal(0, 0.04, size=len(variants)), 0, .2) else: self.payouts = payouts #self.payouts[5] = self.payouts[5] if i < n_trials/2 else 0.1 self.n_trials = n_trials self.total_reward = 0 self.n_k = len(variants) self.shape = (self.n_k, n_trials) def run(self, agent): """Run the simulation with the agent. agent must be a class with choose_k and update methods.""" for i in range(self.n_trials): # agent makes a choice x_chosen = agent.choose_k() # Environment returns reward reward = np.random.binomial(1, p=self.payouts[x_chosen]) # agent learns of reward agent.reward = reward # agent updates parameters based on the data agent.update() self.total_reward += reward agent.collect_data() return self.total_reward 

يتم توزيع النقاط ذات الحدين مع الاحتمال p اعتمادًا على عدد الإجراء (تمامًا كما يمكن توزيعها باستمرار ، لن يتغير الجوهر). سأحدد أيضًا فئة BaseSampler - إنها ضرورية فقط لتخزين السجلات والسمات المختلفة.

 class BaseSampler: def __init__(self, env, n_samples=None, n_learning=None, e=0.05): self.env = env self.shape = (env.n_k, n_samples) self.variants = env.variants self.n_trials = env.n_trials self.payouts = env.payouts self.ad_i = np.zeros(env.n_trials) self.r_i = np.zeros(env.n_trials) self.thetas = np.zeros(self.n_trials) self.regret_i = np.zeros(env.n_trials) self.thetaregret = np.zeros(self.n_trials) self.a = np.ones(env.n_k) self.b = np.ones(env.n_k) self.theta = np.zeros(env.n_k) self.data = None self.reward = 0 self.total_reward = 0 self.k = 0 self.i = 0 self.n_samples = n_samples self.n_learning = n_learning self.e = e self.ep = np.random.uniform(0, 1, size=env.n_trials) self.exploit = (1 - e) def collect_data(self): self.data = pd.DataFrame(dict(ad=self.ad_i, reward=self.r_i, regret=self.regret_i)) 

أدناه نحدد 10 خيارات واسترداد لكل منها. الخيار الأفضل هو الخيار 9 مع استرداد 0.11٪.

 variants = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] payouts = [0.023, 0.03, 0.029, 0.001, 0.05, 0.06, 0.0234, 0.035, 0.01, 0.11] 

من أجل الحصول على شيء للبناء عليه ، نقوم أيضًا بتحديد فئة RandomSampler. هذه الفئة مطلوبة كنموذج أساسي. إنه ببساطة يختار عشوائيًا بشكل عشوائي خيارًا في كل محاولة ولا يقوم بتحديث معلماته.

 class RandomSampler(BaseSampler): def __init__(self, env): super().__init__(env) def choose_k(self): self.k = np.random.choice(self.variants) return self.k def update(self): # nothing to update #self.thetaregret[self.i] = self.thetaregret[self.i] #self.regret_i[self.i] = np.max(self.thetaregret) - self.theta[self.k] #self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.theta) - self.theta[self.k] self.a[self.k] += self.reward self.b[self.k] += 1 self.theta = self.a/self.b self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1 

النماذج الأخرى لديها الهيكل التالي. جميعها لديها طرق اختيار وتحديث. تختار Choose_k الطريقة التي يختار بها الوكيل خيارًا. يقوم التحديث بتحديث معلمات الوكيل - تميز هذه الطريقة كيف تتغير قدرة الوكيل على اختيار الخيار (مع RandomSampler لا تتغير هذه القدرة بأي شكل من الأشكال). نقوم بتشغيل الوكيل في البيئة باستخدام النمط التالي.

 en0 = Environment(machines, payouts, n_trials=10000) rs = RandomSampler(env=en0) en0.run(agent=rs) 

جوهر خوارزمية إبسيلون الجشع هو على النحو التالي.

1. بشكل عشوائي حدد k لمحاولات n.
2. في كل محاولة ، لكل خيار ، تقييم المكاسب.
3. بعد كل المحاولات:
4. مع الاحتمال 1 - e اختر k مع أعلى كسب ؛
5. مع الاحتمال e اختر K بشكل عشوائي.

كود إبسيلون الجشع:

 class eGreedy(BaseSampler): def __init__(self, env, n_learning, e): super().__init__(env, n_learning, e) def choose_k(self): # e% of the time take a random draw from machines # random k for n learning trials, then the machine with highest theta self.k = np.random.choice(self.variants) if self.i < self.n_learning else np.argmax(self.theta) # with 1 - e probability take a random sample (explore) otherwise exploit self.k = np.random.choice(self.variants) if self.ep[self.i] > self.exploit else self.k return self.k # every 100 trials update the successes # update the count of successes for the chosen machine def update(self): # update the probability of payout for each machine self.a[self.k] += self.reward self.b[self.k] += 1 self.theta = self.a/self.b #self.total_reward += self.reward #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k] #self.thetaregret[self.i] = self.thetaregret[self.i] self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k] self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1 

أدناه على الرسم البياني ، يمكنك رؤية نتائج أخذ عينات عشوائية بحتة ، بمعنى آخر ، لا يوجد نموذج هنا. يوضح الرسم البياني الخيار الذي قامت به الخوارزمية في كل محاولة ، إذا كانت هناك 10 آلاف محاولة. تحاول الخوارزمية فقط ، ولكنها لا تتعلم. في المجموع ، سجل 418 نقطة.

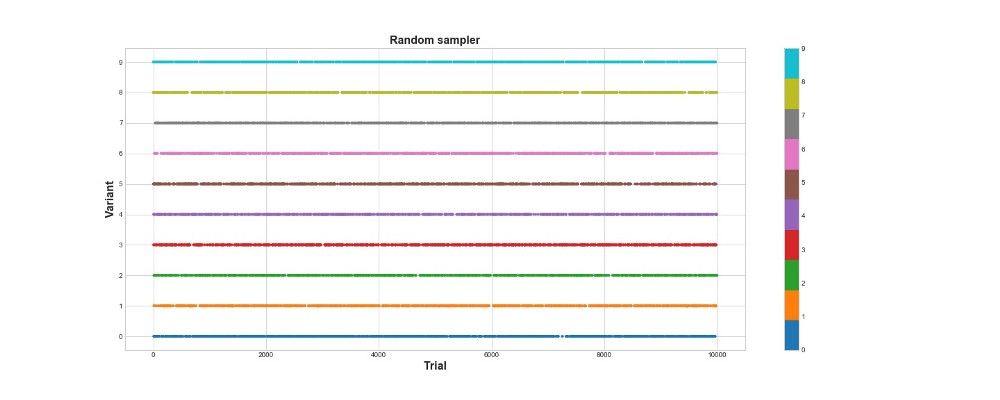
دعونا نرى كيف تتصرف خوارزمية إبسيلون الجشع في نفس البيئة. قم بتشغيل الخوارزمية لـ 10 آلاف محاولة باستخدام e = 0.1 و n_learning = 500 (يحاول الوكيل أول 500 محاولة ، ثم يحاول الاحتمال e = 0.1). دعونا نقيم الخوارزمية وفقًا لإجمالي عدد النقاط التي تسجلها في البيئة.

 en1 = Environment(machines, payouts, n_trials) eg = eGreedy(env=en1, n_learning=500, e=0.1) en1.run(agent=eg) 

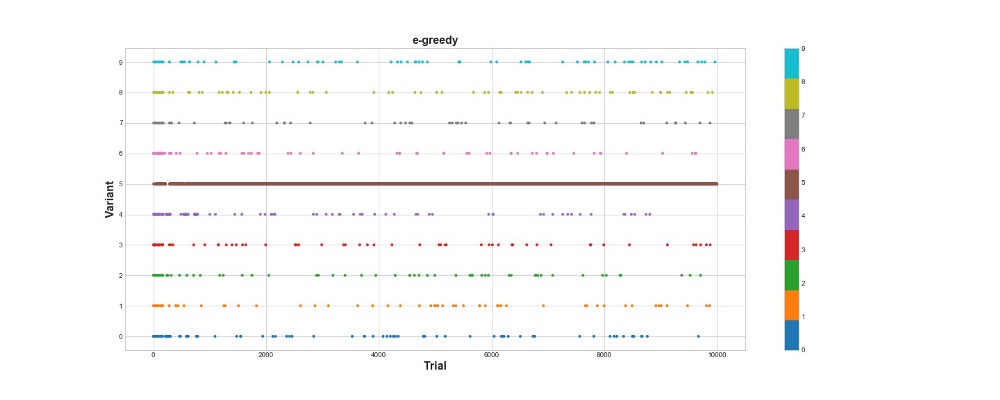
سجلت خوارزمية Epsilon-greedy 788 نقطة ، أفضل مرتين تقريبًا من الخوارزمية العشوائية - فائقة! يوضح الرسم البياني الثاني هذه الخوارزمية بشكل جيد. نرى أنه بالنسبة للخطوات الـ 500 الأولى ، يتم توزيع الإجراءات بالتساوي تقريبًا ويتم اختيار K بشكل عشوائي. ومع ذلك ، فإنه يبدأ في استغلال الخيار 5 بشدة - وهذا خيار قوي جدًا ، ولكنه ليس الأفضل. نرى أيضًا أن الوكيل لا يزال يختار عشوائيًا 10 ٪ من الوقت.

هذا رائع جدًا - لقد كتبنا بضعة أسطر من التعليمات البرمجية ، والآن لدينا بالفعل خوارزمية قوية جدًا يمكنها استكشاف مساحة الخيارات واتخاذ قرارات قريبة من المستوى الأمثل. من ناحية أخرى ، لم تجد الخوارزمية الخيار الأفضل. نعم ، يمكننا زيادة عدد خطوات التعلم ، ولكن بهذه الطريقة سنقضي المزيد من الوقت في البحث العشوائي ، مما يزيد من تفاقم النتيجة النهائية. أيضا ، يتم خياطة العشوائية في هذه العملية بشكل افتراضي - قد لا يتم العثور على أفضل خوارزمية.

سأقوم لاحقًا بتشغيل كل من الخوارزميات عدة مرات حتى نتمكن من مقارنتها ببعضها البعض. ولكن الآن ، دعنا نلقي نظرة على أخذ عينات طومسون واختباره في نفس البيئة.

أخذ عينات طومسون

يختلف أخذ عينات طومسون بشكل أساسي عن خوارزمية إبسيلون الجشع بثلاث نقاط رئيسية:

1. ليس الجشع.
2. يجعل المحاولات بطريقة أكثر تعقيدا.
3. إنه بايزي.

والنقطة الرئيسية هي الفقرة 3 ، والفقرتان 1 و 2 المنبثقة عنها.

جوهر الخوارزمية هو:

1. قم بتعيين توزيع بيتا الأولي بين 0 و 1 لاسترداد كل خيار.
2. قم بتجربة الخيارات من هذا التوزيع ، وحدد الحد الأقصى لمعلمة Theta.
3. اختر الخيار k المرتبط بأكبر ثيتا.
4. عرض عدد النقاط التي تم تسجيلها ، تحديث معلمات التوزيع.

اقرأ المزيد حول توزيع بيتا هنا .
وحول استخدامه في Python - هنا .

كود الخوارزمية:

  class ThompsonSampler(BaseSampler): def __init__(self, env): super().__init__(env) def choose_k(self): # sample from posterior (this is the thompson sampling approach) # this leads to more exploration because machines with > uncertainty can then be selected as the machine self.theta = np.random.beta(self.a, self.b) # select machine with highest posterior p of payout self.k = self.variants[np.argmax(self.theta)] #self.k = np.argmax(self.a/(self.a + self.b)) return self.k def update(self): #update dist (a, b) = (a, b) + (r, 1 - r) self.a[self.k] += self.reward self.b[self.k] += 1 - self.reward # ie only increment b when it's a swing and a miss. 1 - 0 = 1, 1 - 1 = 0 #self.thetaregret[self.i] = self.thetaregret[self.i] #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k] self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k] self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1 

يبدو التدوين الرسمي للخوارزمية مثل هذا.

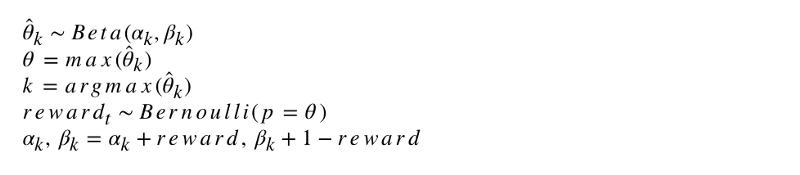
لنبرمج هذه الخوارزمية. مثل العوامل الأخرى ، يرث ThompsonSampler من BaseSampler ويحدد اختياره وطرق التحديث الخاصة به. أطلق الآن وكيلنا الجديد.

  en2 = Environment(machines, payouts, n_trials) tsa = ThompsonSampler(env=en2) en2.run(agent=tsa) 

كما ترون ، سجل أكثر من خوارزمية إبسيلون الجشع. عظيم! دعونا نلقي نظرة على الرسم البياني لاختيار المحاولات. شيئان مثيران للاهتمام يظهران عليه. أولاً ، اكتشف الوكيل بشكل صحيح الخيار الأفضل (الخيار 9) واستخدمه على أكمل وجه. ثانيًا ، استخدم الوكيل خيارات أخرى ، ولكن بطريقة أكثر صعوبة - بعد حوالي 1000 محاولة ، استخدم الوكيل ، بالإضافة إلى الخيار الرئيسي ، بشكل أساسي أقوى الخيارات من بين الخيارات الأخرى. وبعبارة أخرى ، لم يختار بشكل عشوائي ، ولكن بكفاءة أكبر.

لماذا يعمل هذا؟ الأمر بسيط - عدم اليقين في التوزيع الخلفي للفوائد المتوقعة لكل خيار يعني أنه يتم تحديد كل خيار باحتمال يتناسب تقريبًا مع شكله ، يتم تحديده بواسطة معلمات ألفا وبيتا. وبعبارة أخرى ، في كل محاولة ، يؤدي أخذ عينات طومسون إلى تشغيل الخيار وفقًا لاحتمال أن يكون له أقصى فائدة. بشكل تقريبي ، من خلال معلومات التوزيع حول عدم اليقين ، يقرر الوكيل متى يجب فحص البيئة ومتى يتم استخدام المعلومات. على سبيل المثال ، الخيار الضعيف مع عدم اليقين الخلفي المرتفع قد يدفع أكثر مقابل هذه المحاولة. ولكن بالنسبة لمعظم المحاولات ، كلما كان توزيعه الخلفي أقوى ، زاد متوسطه وأقل انحرافه المعياري ، وبالتالي ، زادت فرصة اختياره.

خاصية رائعة أخرى لخوارزمية طومسون: نظرًا لأنها بايزية ، يمكننا تقدير عدم اليقين في تقدير الاسترداد لكل خيار باستخدام معلماته. يوضح الرسم البياني أدناه توزيعات خلفية في 6 نقاط مختلفة وفي 20000 محاولة. سترى كيف تبدأ التوزيعات في الاندماج تدريجياً مع الخيار مع أفضل عائد.

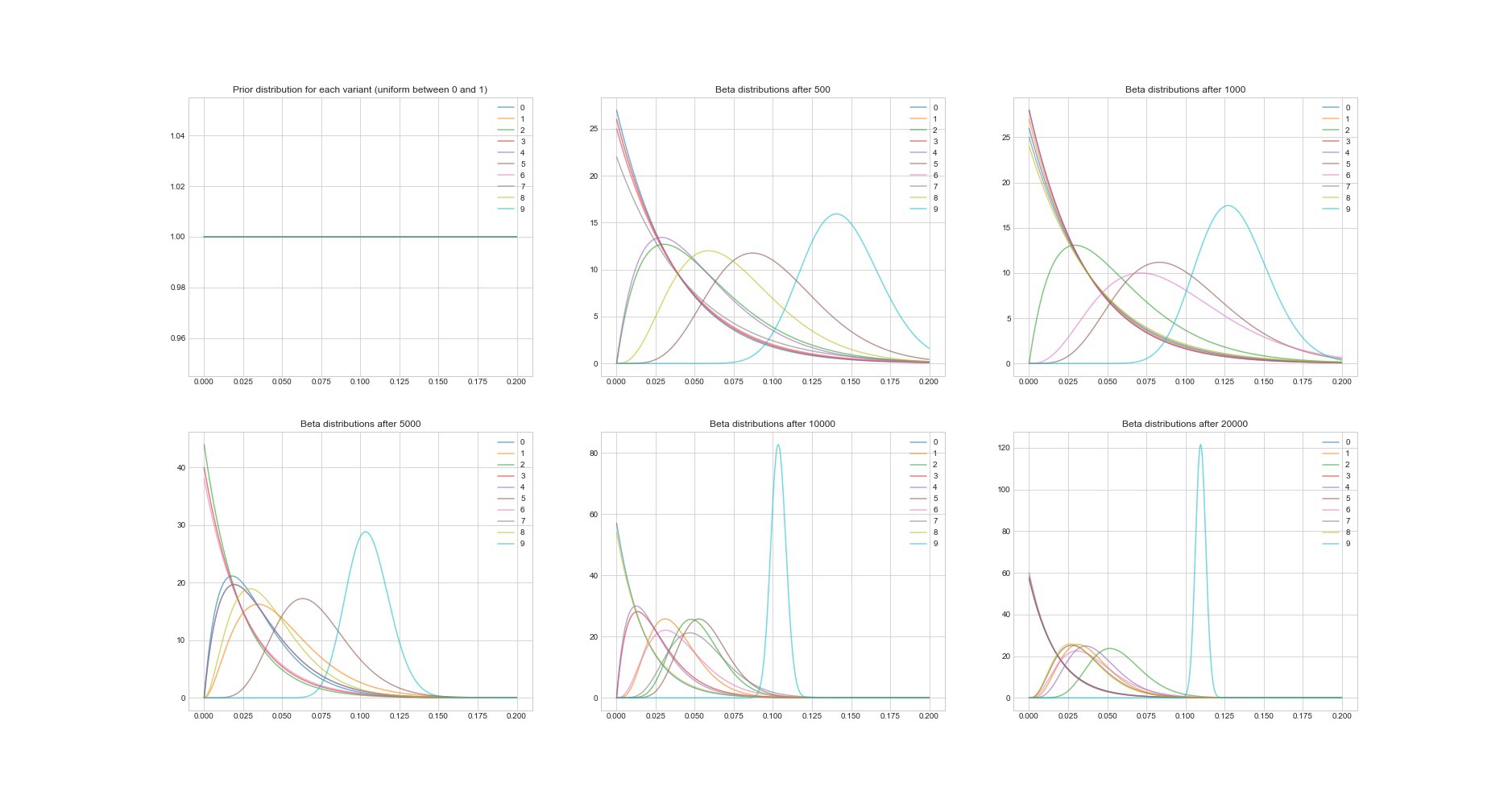
قارن الآن جميع العوامل الثلاثة في 100 محاكاة. 1 محاكاة هي إطلاق وكيل على 10000 محاولات.

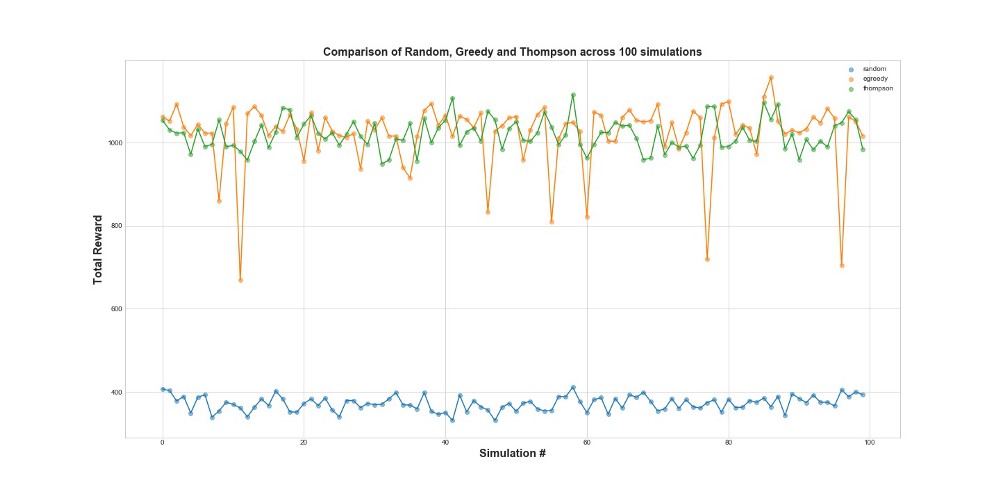
كما ترى من الرسم البياني ، فإن كلا من إستراتيجية إبسيلون-الجشع وأخذ عينات طومسون تعمل بشكل أفضل بكثير من أخذ العينات العشوائية. قد تتفاجأ من أن إستراتيجية إبسيلون الجشع وأخذ عينات طومسون قابلة للمقارنة في الواقع من حيث أدائها. يمكن أن تكون استراتيجية Epsilon-greedy فعالة للغاية ، ولكنها أكثر خطورة ، لأنها يمكن أن تتعثر في خيار دون المستوى الأمثل - يمكن ملاحظة ذلك في حالات الفشل في الرسم البياني. ولكن لا يمكن أخذ عينات طومسون ، لأنه يجعل الاختيار في مساحة الخيارات بطريقة أكثر تعقيدًا.

نأسف

طريقة أخرى لتقييم مدى جودة عمل الخوارزمية هي تقييم الندم. من الناحية التقريبية ، كلما كان أصغر ، كلما كان ذلك أفضل ، فيما يتعلق بالإجراءات المتخذة بالفعل. أدناه رسم بياني للأسف الكلي والندم على الخطأ. مرة أخرى - كلما ندم ، كلما كان ذلك أفضل.

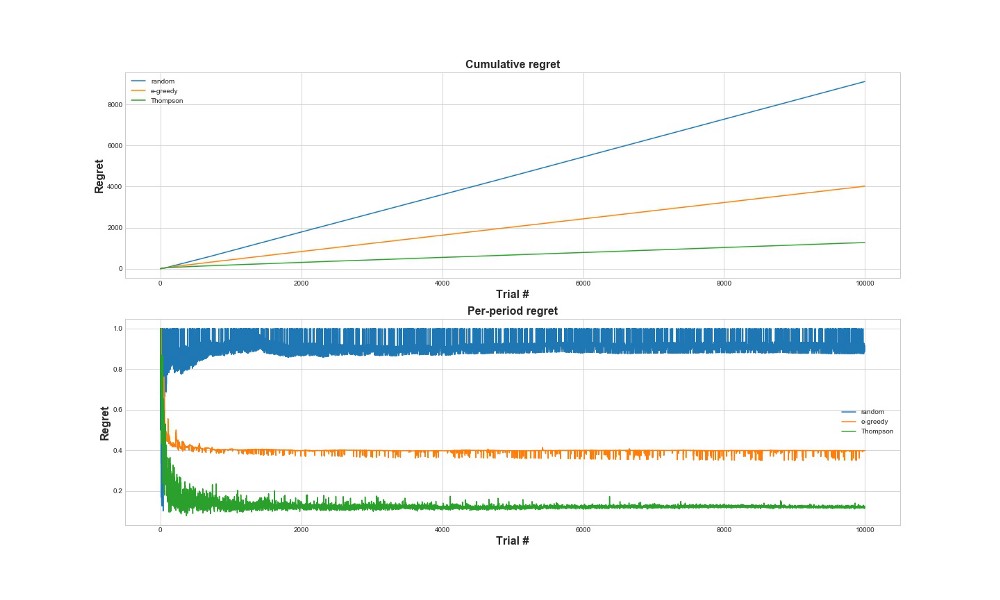
على الرسم البياني العلوي ، نرى الندم الكلي ، وعلى الأسف السفلي المحاولة. كما يتبين من الرسوم البيانية ، تتقارب عملية أخذ عينات طومسون إلى الحد الأدنى من الأسف بشكل أسرع بكثير من استراتيجية إبسيلون-الجشع. ويتقارب إلى مستوى أدنى. مع أخذ عينات Thompson ، يندم الوكيل بشكل أقل لأنه يمكنه اكتشاف أفضل خيار بشكل أفضل وتجربة الخيارات الواعدة بشكل أفضل - لذا فإن أخذ عينات Thompson مناسب بشكل خاص لحالات الاستخدام الأكثر تقدمًا ، مثل النماذج الإحصائية أو الشبكات العصبية لاختيار k.

الاستنتاجات

هذا منشور فني طويل جدا. للتلخيص ، يمكننا استخدام طرق أخذ عينات معقدة إلى حد ما إذا كان لدينا العديد من الخيارات التي نريد اختبارها في الوقت الفعلي. واحدة من الميزات الجيدة جدًا لأخذ عينات Thompson هي أنه يوازن بين الاستخدام والاستكشاف بطريقة صعبة نوعًا ما. أي أنه يمكننا السماح له بتحسين توزيع خيارات الحلول في الوقت الفعلي. هذه خوارزميات رائعة ، ويجب أن تكون مفيدة أكثر للأعمال من اختبارات أ / ب.

هام! لا يعني أخذ عينات طومسون أنك لست بحاجة إلى إجراء اختبارات أ / ب. عادة ، يجدون أولاً أفضل الخيارات بمساعدته ، ثم يقومون بإجراء اختبارات أ / ب عليهم بالفعل.