🤚🏻 🌏 👨‍🔬 حل رمزي للمعادلات التفاضلية الخطية والنظم باستخدام طريقة تحويل لابلاس باستخدام SymPy ↖️ 🍵 👩🏿‍🔬

إن تطبيق الخوارزميات في Python باستخدام الحسابات الرمزية مناسب جدًا لحل مشكلات النمذجة الرياضية للكائنات المحددة بواسطة المعادلات التفاضلية. لحل مثل هذه المعادلات ، يتم استخدام تحويلات لابلاس على نطاق واسع ، والتي ، بعبارات مبسطة ، تجعل من الممكن تقليل المشكلة إلى حل المعادلات الجبرية البسيطة.

في هذا المنشور ، أقترح النظر في وظائف تحويلات لابلاس المباشرة والعكسية من مكتبة SymPy ، والتي تسمح لك باستخدام طريقة لابلاس لحل المعادلات والأنظمة التفاضلية باستخدام Python.

تتم تغطية طريقة لابلاس نفسها ومزاياها في حل المعادلات التفاضلية الخطية والنظم على نطاق واسع في الأدبيات ، على سبيل المثال ، في المنشور الشعبي [1]. في الكتاب ، يتم تقديم طريقة لابلاس للتطبيق في حزم البرامج المرخصة Mathematica و Maple و MATLAB (التي تعني شراء هذا البرنامج من قبل مؤسسة تعليمية) باستخدام أمثلة مختارة من قبل المؤلف.

سنحاول اليوم ألا نفكر في مثال منفصل لحل مشكلة التعلم باستخدام Python ، ولكن طريقة عامة لحل المعادلات التفاضلية الخطية والأنظمة باستخدام وظائف تحويلات لابلاس المباشرة والعكسية. في الوقت نفسه ، سنحفظ لحظة التعلم: سيتم تشكيل الجانب الأيسر من المعادلة التفاضلية الخطية مع شروط كوشي من قبل الطالب نفسه ، وسيتم تنفيذ الجزء الروتيني من المهمة ، التي تتكون في تحويل لابلاس المباشر للجانب الأيمن من المعادلة ، باستخدام دالة laplace_transform () .

قصة تأليف لابلاس يتحول

تحويلات لابلاس (صور لابلاس) لها تاريخ مثير للاهتمام. لأول مرة ، ظهر التكامل في تعريف تحويل لابلاس في أحد أعمال L. Euler. ومع ذلك ، فمن المقبول بشكل عام في الرياضيات استدعاء منهجية أو نظرية اسم عالم الرياضيات الذي اكتشفها بعد أويلر. خلاف ذلك ، سيكون هناك عدة مئات من نظريات أويلر المختلفة.

في هذه الحالة ، كان التالي بعد أويلر عالم الرياضيات الفرنسي بيير سيمون دي لابلاس (بيير سيمون دي لابلاس (1749-1827)). كان هو الذي استخدم مثل هذه التكاملات في عمله على نظرية الاحتمالات. لم يطبق لابلاس نفسه ما يسمى بـ "الأساليب التشغيلية" لإيجاد حلول للمعادلات التفاضلية على أساس تحويلات لابلاس (صور لابلاس). تم اكتشاف هذه الأساليب ونشرها في الواقع من قبل المهندسين العمليين ، وخاصة المهندس الكهربائي الإنجليزي Oliver Heaviside (1850-1925). قبل وقت طويل من إثبات صحة هذه الأساليب بدقة ، تم استخدام حساب التفاضل والتكامل بنجاح وعلى نطاق واسع ، على الرغم من أن شرعيتها كانت موضع تساؤل إلى حد كبير حتى في بداية القرن العشرين ، وكان هناك جدل شديد حول هذا الموضوع.

وظائف تحويل لابلاس المباشر والعكسي

وظيفة تحويل لابلاس المباشر:
تكامل. laplace_transform (t ، s ، ** تلميحات).
تقوم دالة laplace_transform () بتحويلات لابلاس للدالة f (t) للمتغير الحقيقي إلى دالة F (s) للمتغير المعقد ، بحيث:
$F (s) = \ int_ {0} ^ {∞} f (t) e ^ {- st} dt.$

ترجع هذه الدالة (F، a، cond) ، حيث F (s) هي تحويل لابلاس للدالة f (t) ، و <Re (s) هي نصف المستوى حيث يتم تعريف F (s) ، و cond هي شروط مساعدة لتقارب التكامل.
إذا كان لا يمكن حساب التكامل في شكل مغلق ، فتُرجع هذه الدالة كائن LaplaceTransform بدون حوسبة .
إذا قمت بتعيين الخيار noconds = True ، فسوف تُرجع الدالة F (s) فقط .
دالة تحويل لابلاس معكوسة:

تكامل. inverse_laplace_transform (F ، s ، t ، مستوي = بلا ، ** تلميحات).

تقوم الدالة inverse_laplace_transform () بتحويل معكوس لدالة المتغير المركب F (s) إلى الدالة f (t) للمتغير الحقيقي ، بحيث:
$f (t) = \ frac {1} {2 \ pi i} \ int_ {c-∞ \ cdot i} ^ {c + ∞ \ cdot i} e ^ {st} F (s) ds.$

إذا كان لا يمكن حساب التكامل في نموذج مغلق ، فتُرجع هذه الدالة InverseLaplaceTransform للكائن.

يتحول تحويل لابلاس العكسي إلى مثال لتحديد خصائص الانتقال للمنظمين

دالة التحويل لوحدة التحكم PID لها الشكل [2]:

$W (s) = (1+ \ frac {K_ {d} \ cdot T_ {d} \ cdot s} {1 + T_ {d} \ cdot s}) \ cdot K_ {p} \ cdot (1+ \ frac {1} {T_ {i} \ cdot s}) \ cdot \ frac {1} {s}.$

سنكتب برنامجًا للحصول على معادلات للخصائص العابرة لمتحكمات PID و PI من أجل وظيفة النقل المخففة ، بالإضافة إلى اشتقاق الوقت المنقضي في تحويل لابلاس البصري العكسي.

نص البرنامج

#   : from sympy import * import time import matplotlib.pyplot as plt import numpy as np start = time.time() #   : var('s Kp Ti Kd Td') #      : var('t', positive=True) Kp = 2 Ti = 2 Kd = 4 Td = Rational(1, 2) #   -   s: fp = (1 + (Kd * Td * s) / (1 + Td*s)) * Kp * (1 + 1/(Ti*s)) * (1/s) #   -, #     : ht = inverse_laplace_transform(fp, s, t) Kd = 0 #   - (Kd = 0)   s: fpp = (1 + (Kd * Td * s) / (1 + Td*s)) * Kp * (1 + 1/(Ti*s)) * (1/s) #   -, #     : htt = inverse_laplace_transform(fpp, s, t) stop = time.time() print ('     : %ss' % N((stop-start), 3)) #      : f = lambdify(t, ht, 'numpy') F = lambdify(t, htt, 'numpy') tt = np.arange(0.01, 20, 0.05) #  : plt.title('   \n   : \n  - W(s)=%s \n  - W(s)=%s' % (fp, fpp)) plt.plot(tt, f(tt), color='r', linewidth=2, label='-: h(t)=%s' % ht) plt.plot(tt, F(tt), color='b', linewidth=2, label='-: h(t)=%s' % htt) plt.grid(True) plt.legend(loc='best') plt.show()

نحصل على:

عكس وقت تحويل لابلاس البصري: 2.68 ثانية

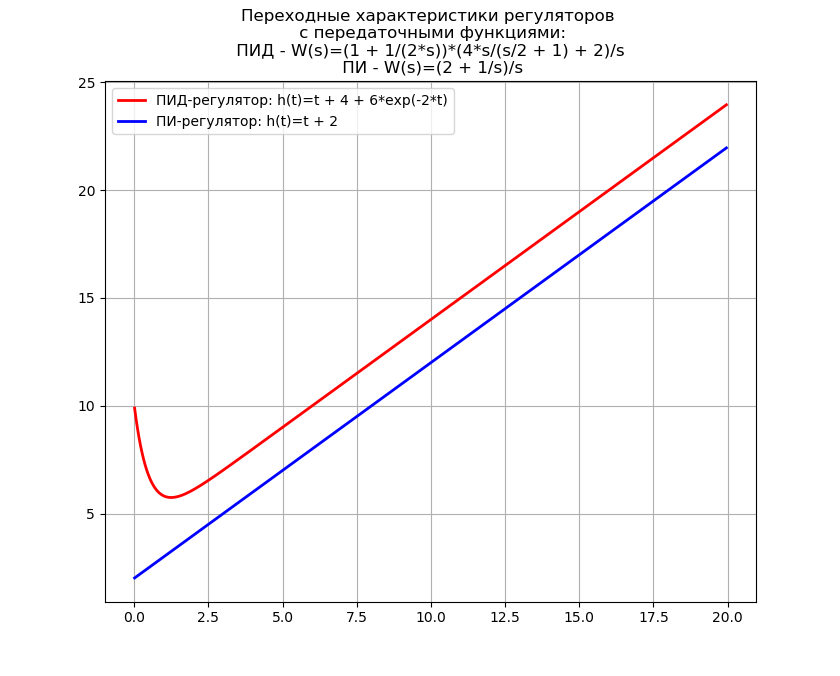
غالبًا ما يتم استخدام تحويل لابلاس العكسي في تركيب البنادق ذاتية الدفع ، حيث يمكن لـ Python استبدال "وحوش" البرامج باهظة الثمن مثل MathCAD ، لذلك فإن استخدام التحويل العكسي أعلاه له أهمية عملية.

تحويل لابلاس من مشتقات أوامر أعلى لحل مشكلة كوشي

سوف تستمر مناقشتنا بتطبيق تحويلات لابلاس (صور لابلاس) للبحث عن حلول لمعادلة تفاضلية خطية ذات معاملات ثابتة للنموذج:

$a \ cdot x '' (t) + b \ cdot x '(t) + c \ cdot x (t) = f (t). (1)$

إذا كان a و b ثوابت ، ثم

$L \ يسار \ {a \ cdot f (t) + b \ cdot q (t) \ right \} = a \ cdot L \ left \ {f (t) \ right \} + b \ cdot L \ left \ {q (t) \ right \} (2)$

لجميع s مثل وجود كلا تحويلات لابلاس (صورة لابلاس) للوظائف f (t) و q (t) .

دعونا نتحقق من الخطية لتحويلات لابلاس المباشرة والعكسية باستخدام الدالتين المدروستين سابقاً laplace_transform () و inverse_laplace_transform () . لهذا ، نأخذ f (t) = sin (3t) ، q (t) = cos (7t) ، a = 5 ، b = 7 كمثال ، ونستخدم البرنامج التالي.

نص البرنامج

 from sympy import* var('sa b') var('t', positive=True) a = 5 f = sin(3*t) b = 7 q = cos(7*t) #   a*L{f(t)}: L1 = a * laplace_transform(f, t, s, noconds=True) #   b*L{q(t)}: L2 = b*laplace_transform(q, t, s, noconds=True) #  a*L{f(t)}+b*L{q(t)}: L = factor(L1 + L2) print (L) #   L{a*f(t)+b*q(t)}: LS = factor(laplace_transform(a*f + b*q, t, s, noconds=True)) print (LS) print (LS == L) #   a* L^-1{f(t)}: L_1 = a * inverse_laplace_transform(L1/a, s, t) #   b* L^-1{q(t)} L_2 = b * inverse_laplace_transform(L2/b, s, t) # a* L^-1{f(t)}+b* L^-1{q(t)}: L_S = L_1 + L_2 print (L_S) #   L^-1{a*f(t)+b*q(t)}: L_1_2 = inverse_laplace_transform(L1 + L2, s, t) print (L_1_2) print (L_1_2 == L_S)

نحصل على:

(7 * ق ** 3 + 15 * ق ** 2 + 63 * ق + 735) / ((ق ** 2 + 9) * (ق ** 2 + 49))
(7 * ق ** 3 + 15 * ق ** 2 + 63 * ق + 735) / ((ق ** 2 + 9) * (ق ** 2 + 49))
صحيح
5 * sin (3 * t) + 7 * cos (7 * t)
5 * sin (3 * t) + 7 * cos (7 * t)

يوضح الرمز أعلاه أيضًا تفرد تحويل لابلاس العكسي.

على افتراض ذلك

$q (t) = f '(t)$ يستوفي شروط النظرية الأولى ، ثم من هذه النظرية ستتبع ما يلي:

$L \ left \ {f '' (t) \ right \} = L \ left \ {q '(t) \ right \} = sL \ left \ {q (t) \ right \} - q (0) = sL \ left \ {f '(t) \ right \} - f' (0) = s \ left [sL \ left \ {f (t) -f (0) \ right \} \ right] ،$

وبالتالي

$L \ left \ {f '' (t) \ right \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f '(0).$

تكرار هذا الحساب يعطي

$L \ left \ {f '' ((t) \ right \} = sL \ left \ {f '' (t) \ right \} - f '' (0) = s ^ {3} F (s) -s ^ {2} f (0) -sf '(0) -f' '(0).$

بعد عدد محدود من هذه الخطوات ، نحصل على التعميم التالي للنظرية الأولى:

$L \ يسار \ {f ^ {(n)} (t) \ right \} = s ^ {n} L \ يسار \ {f (t) \ right \} - s ^ {n-1} f (0 ) -s ^ {n-2} f '(0) - \ cdot \ cdot \ cdot -f ^ {(n-1)} (0) =$

$= s ^ {n} F (s) -s ^ {n-1} f (0) - \ cdot \ cdot \ cdot -sf ^ {(n-2)} (0) -f ^ {(n- 1)} (0). (3)$

من خلال تطبيق العلاقة (3) ، التي تحتوي على مشتقات لابلاس المحولة للدالة المطلوبة بشروط أولية ، إلى المعادلة (1) ، يمكننا الحصول على حلها وفقًا للطريقة التي تم تطويرها خصيصًا في قسمنا بدعم نشط من Scorobey لمكتبة SymPy.

طريقة لحل المعادلات التفاضلية الخطية وأنظمة المعادلات على أساس تحويلات لابلاس باستخدام مكتبة SymPy

لتوضيح الطريقة ، نستخدم معادلة تفاضلية بسيطة تصف حركة نظام يتكون من نقطة مادية من كتلة معينة ، مثبتة على زنبرك يتم تطبيق قوة خارجية عليه. المعادلة التفاضلية والشروط الأولية لهذا النظام لها الشكل التالي:

$x '' + 4x = \ sin (3t) ؛ س (0) = 1.2 ؛ س '(0) = 1 ، (4) دولا$

أين

$x (0)$ - انخفاض الموقف الأولي للكتلة ،

$x '(0)$ - انخفاض سرعة الكتلة الأولية.

نموذج مادي مبسط محدد بالمعادلة (4) بشروط أولية غير صفرية [1]:

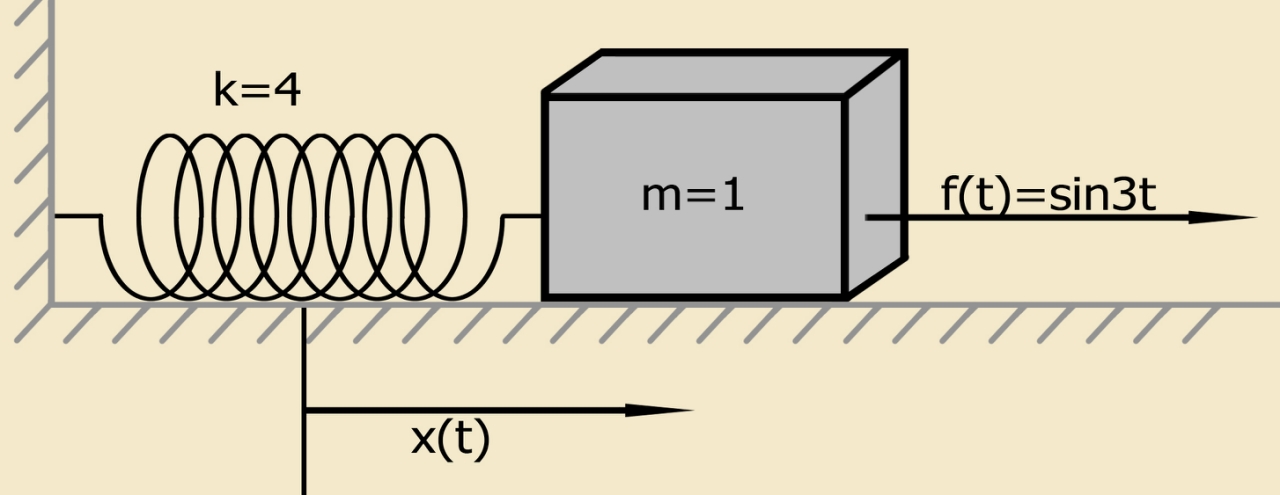
نظام يتكون من نقطة مادية من كتلة معينة مثبتة على زنبرك يفي بمشكلة كوشي (مشكلة في الظروف الأولية). تكون النقطة المادية لكتلة معينة في حالة استرخاء في البداية في وضع التوازن.

لحل هذه المعادلات التفاضلية الخطية وغيرها باستخدام طريقة تحويل لابلاس ، من المناسب استخدام النظام التالي الذي تم الحصول عليه من العلاقات (3):

$L \ left \ {f ^ {IV} (t) \ right \} = s ^ {4} \ cdot F (s) -s ^ {3} \ cdot f (0) -s ^ {2} \ cdot f ^ {I} (0) -s \ cdot f ^ {II} (0) -f ^ {III} (0)،$

$L \ left \ {f ^ {III} (t) \ right \} = s ^ {3} \ cdot f (s) -s ^ {2} \ cdot f (0) -s \ cdot f ^ {I } (0) -f ^ {II} (0)،$

$L \ left \ {f ^ {II} (t) \ right \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f ^ {I} (0)،$

$L \ يسار \ {f ^ {I} (t) \ right \} = s \ cdot F (s) -f (0) ، L \ left \ {f (t) \ right \} = F (s) .$

$L \ يسار \ {f (t) \ right \} = F (s). (5)$

تسلسل الحلول باستخدام SymPy كما يلي:

تحميل الوحدات اللازمة وتحديد المتغيرات الرمزية بشكل صريح:

 from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function)

تحديد إصدار مكتبة sympy لمراعاة ميزاتها. للقيام بذلك ، أدخل الأسطر التالية:
```
 import SymPy print ('  sympy – %' % (sympy._version_)) 
```
وفقًا للمعنى المادي للمشكلة ، يتم تحديد المتغير الزمني لمنطقة بما في ذلك الأعداد الصفرية والإيجابية. وضعنا الشروط الأولية والدالة على الجانب الأيمن من المعادلة (4) مع تحويل لابلاس اللاحق لها. بالنسبة للظروف الأولية ، يجب عليك استخدام الدالة Rational ، حيث يؤدي استخدام التقريب العشري إلى حدوث خطأ.
```
 #    : x0 = Rational(6, 5) #   : x01 = Rational(1, 1) g = sin(3*t) Lg = laplace_transform(g, t, s, noconds=True) 
```
باستخدام (5) ، نعيد كتابة المشتقات المحولة من لابلاس المتضمنة في الجانب الأيسر من المعادلة (4) ، لتشكيل الجانب الأيسر من هذه المعادلة منها ، ومقارنة النتيجة بالجانب الأيمن:
```
 d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = d2 + 4*d0 de = Eq(d, Lg) 
```
نحل المعادلة الجبرية التي تم الحصول عليها للتحويل X (s) وإجراء تحويل لابلاس العكسي:
```
 rez = solve(de, X(s))[0] soln = inverse_laplace_transform(rez, s, t) 
```
ننتقل من العمل في مكتبة SymPy إلى مكتبة NumPy:
```
 f = lambdify(t, soln, 'numpy') 
```

نرسم طريقة بايثون المعتادة:

 x = np.linspace(0, 6*np.pi, 100) plt.title(',     \n  :\n  (t)=%s' % soln) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()

النص الكامل للبرنامج:

 from sympy import * import numpy as np import matplotlib.pyplot as plt import sympy var('s') var('t', positive=True) var('X', cls=Function) print ("  sympy – %s" % (sympy.__version__)) #       : x0 = Rational(6, 5) #       : x01 = Rational(1, 1) g = sin(3*t) #   : Lg = laplace_transform(g, t, s, noconds=True) d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = d2 + 4*d0 de = Eq(d, Lg) #   : rez = solve(de, X(s))[0] #   : soln = inverse_laplace_transform(rez, s, t) f = lambdify(t, soln, "numpy") x = np.linspace(0, 6*np.pi, 100) plt.title(',     \n  :\n  (t)=%s' % soln) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()

نحصل على:
إصدار مكتبة Sympy - 1.3

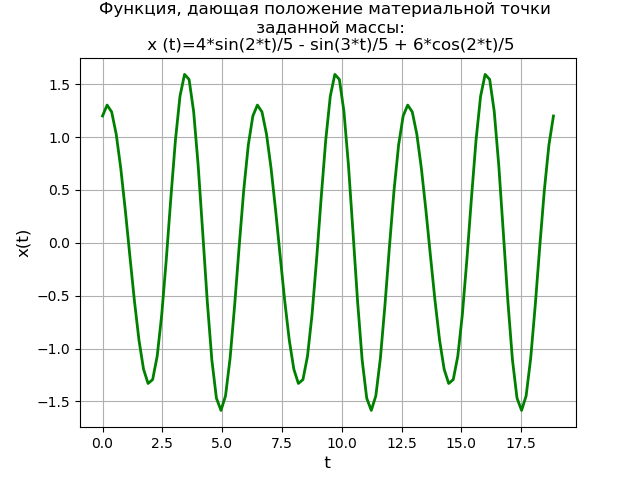
يتم الحصول على رسم بياني للدالة الدورية يعطي موقع نقطة المادة لكتلة معينة. تقدم طريقة تحويل لابلاس باستخدام مكتبة SymPy حلاً ليس فقط بدون الحاجة إلى إيجاد حل عام لمعادلة متجانسة وحل خاص للمعادلة التفاضلية غير المتجانسة الأولية ، ولكن أيضًا بدون الحاجة إلى استخدام طريقة الكسر الأولية وجداول لابلاس.

في الوقت نفسه ، يتم الحفاظ على القيمة التعليمية لطريقة الحل بسبب الحاجة إلى استخدام النظام (5) وانتقل إلى NumPy لدراسة الحلول باستخدام طرق أكثر إنتاجية.

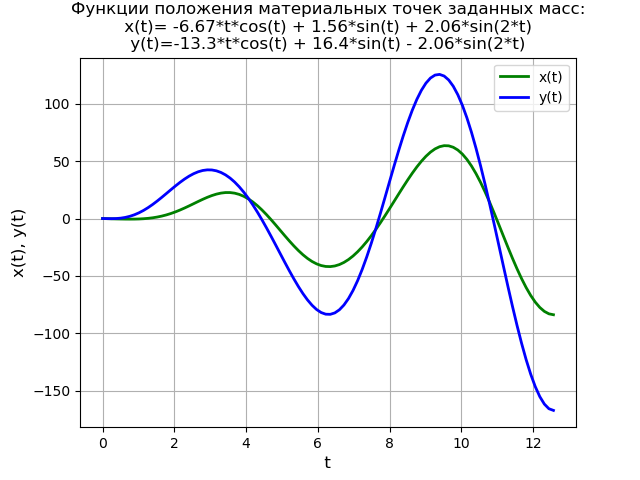
لإثبات الطريقة ، نحل نظام المعادلات التفاضلية:

$\ start {cases} 2x '' + 6x-2 = 0، \\ y '' - 2x + 2y = 40 \ cdot \ sin (3t)، \ end {cases} (6)$
بشروط أولية

$x (0) = y (0) = y '(0) = 0.$

نموذج فيزيائي مبسط يحدده نظام المعادلات (6) تحت شروط أولية صفرية:

وبالتالي ، يتم تطبيق القوة f (t) فجأة على نقطة المادة الثانية لكتلة معينة في الوقت t = 0 ، عندما يكون النظام في حالة استقرار في وضع التوازن.

حل نظام المعادلات مطابق للحل الذي تم دراسته سابقًا للمعادلة التفاضلية (4) ، لذلك أعطي نص البرنامج بدون تفسير.

نص البرنامج

 from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t ', positive=True) var('X Y', cls=Function) x0 = 0 x01 = 0 y0 = 0 y01 = 0 g = 40 * sin(3*t) Lg = laplace_transform(g, t, s, noconds=True) de1 = Eq(2*(s**2*X(s) - s*x0 - x01) + 6*X(s) - 2*Y(s)) de2 = Eq(s**2*Y(s) - s*y0 - y01 - 2*X(s) + 2*Y(s) - Lg) rez = solve([de1, de2], X(s), Y(s)) rezX = expand(rez[X(s)]) solnX = inverse_laplace_transform(rezX, s, t) rezY = expand(rez[Y(s)]) solnY = inverse_laplace_transform(rezY, s, t) f = lambdify(t, solnX, "numpy") F = lambdify(t, solnY, "numpy") x = np.linspace(0, 4*np.pi, 100) plt.title('     :\nx(t)=%s\ny(t)=%s' % (solnX, solnY)) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t), y(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2, label='x(t)') plt.plot(x, F(x), 'b', linewidth=2, label='y(t)') plt.legend(loc='best') plt.show()

نحصل على: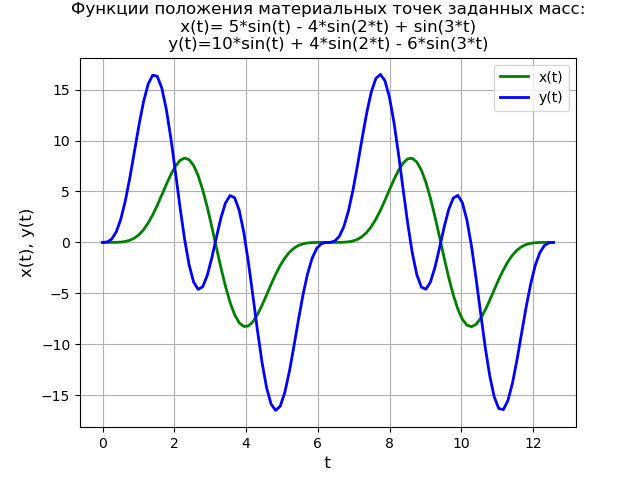

بالنسبة للظروف الأولية غير الصفرية ، سيأخذ نص البرنامج والرسم البياني للوظيفة الشكل التالي:

نص البرنامج

 from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X Y', cls=Function) x0 = 0 x01 = -1 y0 = 0 y01 = -1 g = 40 * sin(t) Lg = laplace_transform(g, t, s, noconds=True) de1 = Eq(2*(s**2*X(s) - s*x0 - x01) + 6*X(s) - 2*Y(s)) de2 = Eq(s**2*Y(s) - s*y0 - y01 - 2*X(s) + 2*Y(s) - Lg) rez = solve([de1, de2], X(s), Y(s)) rezX = expand(rez[X(s)]) solnX = (inverse_laplace_transform(rezX, s, t)).evalf().n(3) rezY = expand(rez[Y(s)]) solnY = (inverse_laplace_transform(rezY, s, t)).evalf().n(3) f = lambdify(t, solnX, "numpy") F = lambdify(t, solnY, "numpy") x = np.linspace(0, 4*np.pi, 100) plt.title('     :\nx(t)= %s \ny(t)=%s' % (solnX, solnY)) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t), y(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2, label='x(t)') plt.plot(x, F(x), 'b', linewidth=2, label='y(t)') plt.legend(loc='best') plt.show()

خذ بعين الاعتبار حل معادلة تفاضلية خطية من الدرجة الرابعة بشروط أولية صفرية:

$x ^ {(4)} + 2 \ cdot x '' + x = 4 \ cdot t \ cdot e ^ {t} ؛$

$x (0) = x '(0) = x' '(0) = x ^ {(3)} (0) = 0.$

نص البرنامج:

 from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function) #  : x0 = 0 x01 = 0 x02 = 0 x03 = 0 g = 4*t*exp(t) #   : Lg = laplace_transform(g, t, s, noconds=True) d4 = s**4*X(s) - s**3*x0 - s**2*x01 - s*x02 - x03 d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = factor(d4 + 2*d2 + d0) de = Eq(d, Lg) #   : rez = solve(de, X(s))[0] #   : soln = inverse_laplace_transform(rez, s, t) f = lambdify(t, soln, "numpy") x = np.linspace(0, 6*np.pi, 100) plt.title(':\n  (t)=%s\n' % soln, fontsize=11) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()

جدول القرار:

نحل المعادلة التفاضلية الخطية من الرتبة الرابعة:

$x ^ {(4)} + 13x '' + 36x = 0 ؛$
بشروط أولية

$x (0) = x '' (0) = 0$ ،

$x '(0) = 2$ ،

$x ^ {(3)} (0) = - 13$ .

نص البرنامج:

 from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function) #  : x0 = 0 x01 = 2 x02 = 0 x03 = -13 d4 = s**4*X(s) - s**3*x0 - s**2*x01 - s*x02 - x03 d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = factor(d4 + 13*d2 + 36*d0) de = Eq(d, 0) #   : rez = solve(de, X(s))[0] #   : soln = inverse_laplace_transform(rez, s, t) f = lambdify(t, soln, "numpy") x = np.linspace(0, 6*np.pi, 100) plt.title(':\n  (t)=%s\n' % soln, fontsize=11) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()

جدول القرار: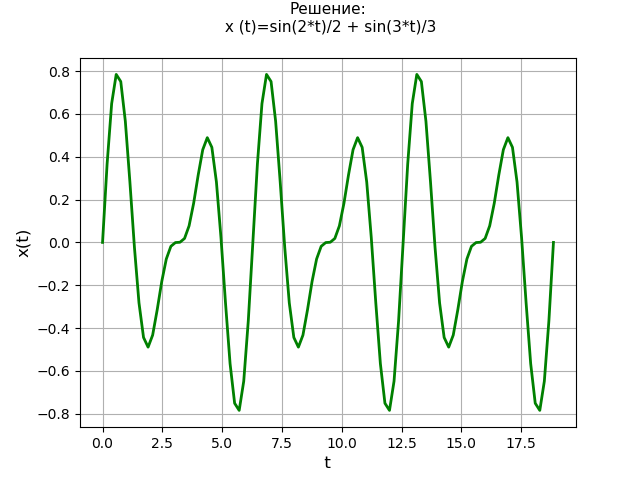

وظائف لحل ODE

بالنسبة لأنظمة ODE و ODE مع حل تحليلي ، يتم استخدام وظيفة dsolve () :
sympy.solvers.ode. dsolve (eq، func = None، hint = 'default'، simpleify = True، ics = None، xi = None، eta = None، x0 = 0، n = 6، ** kwargs)

دعنا نقارن أداء دالة dsolve () مع طريقة لابلاس. على سبيل المثال ، خذ المعادلة التفاضلية من الدرجة الرابعة التالية بشروط أولية صفرية:

$x ^ {(IV)} (t) = 3 \ cdot x '' (t) -x (t) = 4 \ cdot t \ cdot \ exp (t) ؛$

$x (0) = x '(0) = x' '(0) = x' '(0) = 0.$

برنامج يستخدم وظيفة dsolve ():

 from sympy import * import time import numpy as np import matplotlib.pyplot as plt start = time.time() var('t C1 C2 C3 C4') u = Function("u")(t) #   : de = Eq(u.diff(t, t, t, t) - 3*u.diff(t, t, t) + 3*u.diff(t, t) - u.diff(t), 4*t*exp(t)) #   : des = dsolve(de, u) #  : eq1 = des.rhs.subs(t, 0) eq2 = des.rhs.diff(t).subs(t, 0) eq3 = des.rhs.diff(t, t).subs(t, 0) eq4 = des.rhs.diff(t, t, t).subs(t, 0) #       : seq = solve([eq1, eq2-1, eq3-2, eq4-3], C1, C2, C3, C4) rez = des.rhs.subs([(C1, seq[C1]), (C2, seq[C2]), (C3, seq[C3]), (C4, seq[C4])]) def F(t): return rez f = lambdify(t, rez, 'numpy') x = np.linspace(0, 6*np.pi, 100) stop = time.time() print ('      dsolve(): %ss' % round((stop-start), 3)) plt.title('    dsolve():\n  (t)=%s\n' % rez, fontsize=11) plt.grid(True) plt.xlabel('Time t seconds', fontsize=12) plt.ylabel('f(t)', fontsize=16) plt.plot(x, f(x), color='#008000', linewidth=3) plt.show()

نحصل على:

وقت المعادلة باستخدام دالة dsolve (): 1.437 ثانية

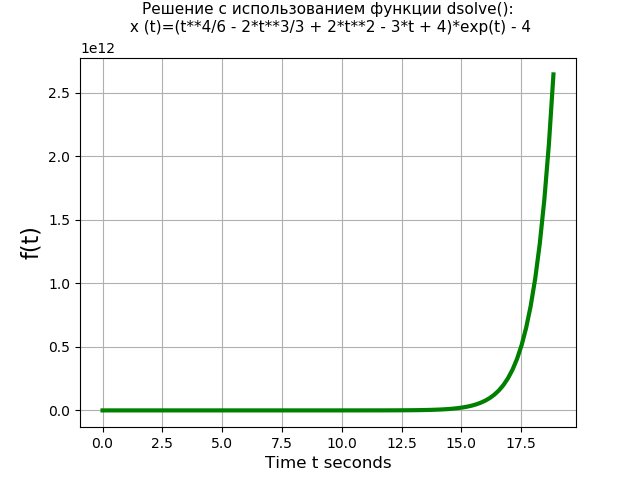
برنامج يستخدم تحويل لابلاس:

 from sympy import * import time import numpy as np import matplotlib.pyplot as plt start = time.time() var('s') var('t', positive=True) var('X', cls=Function) #  : x0 = 0 x01 = 0 x02 = 0 x03 = 0 #     : g = 4*t*exp(t) #   : Lg = laplace_transform(g, t, s, noconds=True) d4 = s**4*X(s) - s**3*x0 - s**2*x01 - s*x02 - x03 d3 = s**3*X(s) - s**2*x0 - s*x01 - x02 d2 = s**2*X(s) - s*x0 - x01 d1 = s*X(s) - x0 d0 = X(s) #     : d = factor(d4 - 3*d3 + 3*d2 - d1) de = Eq(d, Lg) #   : rez = solve(de, X(s))[0] #   : soln = collect(inverse_laplace_transform(rez, s, t), t) f = lambdify(t, soln, 'numpy') x = np.linspace(0, 6*np.pi, 100) stop = time.time() print ('      : %ss' % round((stop-start), 3)) plt.title('    :\n  (t)=%s\n' % soln, fontsize=11) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()

نحصل على:

وقت المعادلة باستخدام تحويل لابلاس: 3.274 ثانية

لذا ، تحل الدالة dsolve () (1.437 s) معادلة الترتيب الرابع أسرع من حلها باستخدام طريقة تحويل لابلاس (3.274 ثانية) أكثر من مرتين. ومع ذلك ، تجدر الإشارة إلى أن الدالة dsolve () لا تحل نظام المعادلات التفاضلية من الدرجة الثانية ، على سبيل المثال ، عند حل النظام (6) باستخدام الدالة dsolve () ، يحدث خطأ:

 from sympy import* t = symbols('t') x, y = symbols('x, y', Function=True) eq = (Eq(Derivative(x(t), t, 2), -3*x(t) + y(t)), Eq(Derivative(y(t), t, 2), 2*x(t) - 2*y(t) + 40*sin(3*t))) rez = dsolve(eq) print (list(rez))

نحصل على:

liftNotImplementedError
لم يتم تنفيذ الخطأ

يعني هذا الخطأ أنه لا يمكن تمثيل حل نظام المعادلات التفاضلية باستخدام الدالة dsolve () بشكل رمزي. في حين أنه بمساعدة تحويلات لابلاس حصلنا على تمثيل رمزي للحل ، وهذا يثبت فعالية الطريقة المقترحة.

ملاحظة

من أجل إيجاد الطريقة اللازمة لحل المعادلات التفاضلية باستخدام الدالة dsolve () ، تحتاج إلى استخدام classify_ode (eq، f (x)) ، على سبيل المثال:

 from sympy import * from IPython.display import * import matplotlib.pyplot as plt init_printing(use_latex=True) x = Symbol('x') f = Function('f') eq = Eq(f(x).diff(x, x) + f(x), 0) print (dsolve(eq, f(x))) print (classify_ode(eq, f(x))) eq = sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x) print (classify_ode(eq, f(x))) rez = dsolve(eq, hint='almost_linear_Integral') print (rez)

نحصل على:

Eq (f (x)، C1 * sin (x) + C2 * cos (x))
('nth_linear_constant_coeff_homogeneous'، '2nd_power_series_ordinary')
("يفصل" ، "1st_exact" ، "almost_linear" ، "1st_power_series" ، "lie_group" ، "Separable_Integral" ، "1st_exact_Integral" ، "almost_linear_Integral")
[المعادل (f (x) ، -acos ((C1 + Integral (0، x)) * exp (-Integral (-tan (x)، x))) + 2 * pi) ، Eq (f (x) ، acos ((C1 + Integral (0، x)) * exp (-Integral (-tan (x)، x)))]]]

وبالتالي ، بالنسبة للمعادلة eq = Eq (f (x) .diff (x، x) + f (x)، 0) ، فإن أي طريقة من القائمة الأولى تعمل:

nth_linear_constant_coeff_hogogeneous ،
2nd_power_series_ordinary

بالنسبة للمعادلة eq = sin (x) * cos (f (x)) + cos (x) * sin (f (x)) * f (x) .diff (x) ، تعمل أي طريقة من القائمة الثانية:

قابل للانفصال ، 1st_exact ، تقريبًا ، خطي ،
1st_power_series، lie_group، Separable_Integral،
1st_exact_Integral ، تقريبا_خطية_التكامل

لاستخدام الطريقة المحددة ، سيأخذ إدخال وظيفة dsolve () الشكل ، على سبيل المثال:

 rez = dsolve(eq, hint='almost_linear_Integral')

الخلاصة:

تهدف هذه المقالة إلى إظهار كيفية استخدام أدوات مكتبات SciPy و NumPy على سبيل المثال في حل أنظمة ODE الخطية باستخدام طريقة المشغل. وهكذا ، تم النظر في طرق الحل الرمزي للمعادلات التفاضلية الخطية وأنظمة المعادلات بطريقة لابلاس. يتم تنفيذ تحليل أداء هذه الطريقة والأساليب المطبقة في وظيفة dsolve ().

المراجع:

المعادلات التفاضلية ومشكلات القيمة الحدية: النمذجة والحساب باستخدام الرياضيات ، القيقب و MATLAB. الطبعة الثالثة.: Per. من اللغة الإنجليزية - م: LLC "I.D. وليامز ، 2008. - 1104 ص: سوء. - Paral. حلمة الثدي. الإنجليزية
استخدام تحويل لابلاس العكسي لتحليل الروابط الديناميكية لأنظمة التحكم

حل رمزي للمعادلات التفاضلية الخطية والنظم باستخدام طريقة تحويل لابلاس باستخدام SymPy

قصة تأليف لابلاس يتحول

وظائف تحويل لابلاس المباشر والعكسي

يتحول تحويل لابلاس العكسي إلى مثال لتحديد خصائص الانتقال للمنظمين

تحويل لابلاس من مشتقات أوامر أعلى لحل مشكلة كوشي

طريقة لحل المعادلات التفاضلية الخطية وأنظمة المعادلات على أساس تحويلات لابلاس باستخدام مكتبة SymPy

وظائف لحل ODE

الخلاصة:

More articles: