تعلم برنامج OpenGL. الدرس 6.1. PBR أو التقديم الصحيح جسديا. النظرية

التقديم الصحيح جسديا

PBR ، أو العرض الجسدي ، هي مجموعة من تقنيات التصور القائمة على نظرية تتوافق تمامًا مع النظرية الحقيقية لانتشار الضوء. نظرًا لأن الغرض من PBR هو محاكاة موثوقة جسديًا للضوء ، فإنه يبدو أكثر واقعية مقارنة بنماذج الإضاءة Phong و Blinn-Fong التي استخدمناها سابقًا. إنه لا يبدو أفضل فحسب ، بل يعطي أيضًا تقريبًا جيدًا للفيزياء الحقيقية ، مما يسمح لنا (والفنانين على وجه الخصوص) بإنشاء مواد تستند إلى الخصائص الفيزيائية للأسطح دون اللجوء إلى الحيل الرخيصة لجعل الإضاءة تبدو واقعية. الميزة الرئيسية لهذا النهج هي أن المواد التي نقوم بإنشائها ستبدو كما هو مخطط لها بغض النظر عن ظروف الإضاءة ، والتي لا يمكن قولها عن طرق أخرى ، وليس PBR.

ومع ذلك ، لا يزال PBR تقريبًا للواقع (استنادًا إلى قوانين الفيزياء) ، ولهذا السبب يطلق عليه العرض الصحيح جسديًا بدلاً من العرض المادي. حتى يمكن تسمية نموذج الإضاءة بشكل صحيح ماديًا ، يجب أن يستوفي 3 شروط (لا تقلق ، سنصل إليهم قريبًا):

• بناء على نموذج الأوجه الدقيقة العاكسة
• الامتثال لقانون الحفاظ على الطاقة
• استخدام دالة توزيع الانعكاس المزدوج الحزمة (BRDF)

في هذه السلسلة التعليمية ، سنركز على نهج PBR ، الذي تم تطويره في الأصل في ديزني وتم تكييفه للتصور في الوقت الحقيقي بواسطة Epic Games. نهجهم ، القائم على سير عمل عازل معدني (سير العمل المعدني ، لم يتمكن من العثور على ترجمة أفضل - محرر تقريبًا ) ، موثق جيدًا ومقبول على نطاق واسع في العديد من المحركات الشائعة ويبدو مذهلاً. في نهاية هذا القسم ، نحصل على شيء مشابه لما يلي:

ضع في اعتبارك أن المقالات في هذا القسم متقدمة جدًا ، لذا يوصى بأن يكون لديك فهم جيد لإضاءة OpenGL وإضاءة التظليل. إليك بعض المعرفة التي ستحتاجها لدراسة هذا القسم: ذاكرة التخزين المؤقت للإطارات ، والخرائط التكعيبية ، وتصحيح جاما ، و HDR ، والخرائط العادية . سنتعمق أيضًا في الرياضيات ، لكنني أعد بأن أفعل كل شيء ممكن لشرح كل شيء بأكبر قدر ممكن من الوضوح.

نموذج الأوجه الدقيقة العاكسة

تعتمد جميع تقنيات PBR على نظرية الوجوه الدقيقة. تقول هذه النظرية أنه يمكن تمثيل كل سطح بتكبير عالي كمجموعة من المرايا المجهرية تسمى الوجوه الدقيقة . بسبب خشونة السطح ، يمكن توجيه هذه المرايا الدقيقة في اتجاهات مختلفة:

كلما كان السطح أكثر خشونة ، كلما كانت وجوهه الدقيقة موجهة بشكل عشوائي. نتيجة هذا الترتيب لهذه المرايا الصغيرة هي (على وجه الخصوص عندما يتعلق الأمر بالمشاعل والانعكاسات المرآوية) أن أشعة الضوء الساقط متناثرة في اتجاهات مختلفة على الأسطح الخشنة ، مما يؤدي إلى اشتعال مرآوي أوسع. والعكس بالعكس: على الأسطح الملساء ، من المرجح أن تنعكس الأشعة السائلة في اتجاه واحد ، مما سيعطي وهجًا أصغر وأكثر حدة:

على المستوى المجهري ، لا توجد أسطح ناعمة تمامًا ، ولكن نظرًا لأن الوجوه الدقيقة صغيرة بما يكفي ولا يمكننا التمييز بينها داخل مساحة البكسل ، فإننا نقترب إحصائيًا من خشونة السطح من خلال تقديم معامل الخشونة . باستخدام هذا المعامل ، يمكننا حساب جزء الوجوه الدقيقة الموجهة باتجاه ناقل معين $$$h$ . هذا المتجه $$$h$ لا شيء أكثر من متجه متوسط ​​يقع في المنتصف بين اتجاه الضوء الساقط $$$l$ واتجاه المراقب $$$v$ . تحدثنا عنها في وقت سابق في درس حول الإضاءة المتقدمة ، حيث حددناها على أنها نسبة مجموع المتجهات $$$l$ و $$$v$ إلى طول المتجه الناتج:

$$

$$h = \ frac {l + v} {|| l + v ||}$$

كلما كانت الوجوه الدقيقة أكثر اتجاهًا نحو المتجه الوسيط ، كلما كان تمييز الضوء أكثر حدة وإشراقًا. نظرًا لمعامل الخشونة ، الذي يقع بين 0 و 1 ، يمكننا تقريبًا إحصائيًا اتجاه الوجوه الدقيقة:

كما ترون ، فإن القيمة الأعلى لمعامل الخشونة تعطي بقعة مضيئة بحجم أكبر ، مقارنة مع بقعة صغيرة وحادة على الأسطح الملساء.

الحفاظ على الطاقة.

إن استخدام التقريب مع مراعاة الوجوه الدقيقة يحمل بالفعل شكلاً معينًا من أشكال الحفاظ على الطاقة: لن تتجاوز طاقة الضوء المنعكس طاقة الضوء الساقط (إذا لم يسطع السطح من تلقاء نفسه). بالنظر إلى الصورة أعلاه ، نرى أنه مع زيادة خشونة السطح ، تزداد بقعة الضوء المنعكس ، ولكن في نفس الوقت ينخفض ​​سطوعه. إذا كانت شدة الضوء المنعكس هي نفسها لجميع وحدات البكسل ، بغض النظر عن حجم البقعة ، فإن الأسطح الخشنة ستصدر المزيد من الطاقة ، مما ينتهك قانون الحفاظ على الطاقة. لذلك ، فإن الانعكاسات المرآوية أكثر سطوعًا على الأسطح الملساء وخافتة على الأسطح الخشنة.

من أجل الحفاظ على الطاقة ، يجب علينا أن نفصل بوضوح بين المكونات المنتشرة والمرآة. في تلك اللحظة ، عندما يصل شعاع من الضوء إلى السطح ، ينقسم إلى مكونات منعكسة ومنكسرة . العنصر المنعكس هو الضوء المنعكس مباشرة ولا يخترق السطح ؛ نحن نعرفه كمكون مرآة للضوء. المكون المنكسر هو ضوء يخترق السطح ويمتصه - وهو معروف لنا كمكون منتشر للضوء.

ولكن هناك بعض الفروق الدقيقة المرتبطة بامتصاص الضوء - لا يحدث على الفور بمجرد أن يلمس الضوء السطح. من مسار الفيزياء ، نعلم أنه يمكن وصف الضوء بأنه شعاع من الفوتونات بطاقة تتحرك في خط مستقيم حتى يفقد كل الطاقة نتيجة الاصطدام بالعقبات. تتكون كل مادة من جزيئات دقيقة يمكن أن تتفاعل مع شعاع من الضوء ، كما هو موضح في الشكل أدناه. تمتص هذه الجسيمات جزءًا أو كل طاقة الضوء في كل تصادم ، وتحويله إلى حرارة.

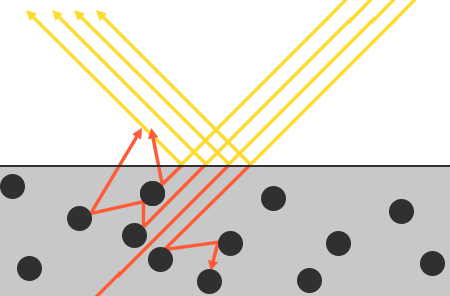
في الحالة العامة ، لا يتم امتصاص كل الطاقة ، ويستمر الضوء في الانتشار في اتجاهات عشوائية (في الغالب) ، حيث يتصادم مرة أخرى مع جزيئات أخرى حتى ينفد من الطاقة أو يترك السطح مرة أخرى. وهكذا ، يبدأ السطح في إعادة إطلاق أشعة الضوء ، مما يساهم في شكل اللون المرئي (المنتشر) للسطح. باستخدام PBR ، نقوم بافتراض مبسط أن كل الضوء المنكسر يتم امتصاصه وتناثره على مساحة صغيرة من التأثير ، متجاهلين تأثير الضوء المتناثر الذي يترك السطح على مسافة من هذه المنطقة. تقنيات التظليل الخاصة التي تأخذ هذا في الاعتبار ، والمعروفة باسم تقنيات التشتت تحت السطح ، تعزز بشكل كبير الجودة البصرية للمواد مثل الجلد والرخام والشمع ، ولكنها مكلفة من حيث الأداء.

تظهر التفاصيل الدقيقة الإضافية عند انكسار الضوء وانعكاسه على الأسطح المعدنية . تتفاعل الأسطح المعدنية بشكل مختلف مع الضوء عن غير المعدني (أي العوازل). إنهم يطيعون نفس قوانين الانكسار والانعكاس ، باستثناء واحد: يمتص كل الضوء المنكسر على السطح دون تشتت ، يبقى فقط الضوء المنعكس على المرآة ؛ وبعبارة أخرى ، فإن الأسطح المعدنية ليس لها لون منتشر. بسبب هذا الاختلاف الواضح بين المعادن والعزل الكهربائي ، ستتم معالجتها بشكل مختلف في ناقل PBR الذي سنذهب فيه إلى أبعد من هذا المقال.

يقودنا هذا الاختلاف بين الضوء المنعكس والمنكسر إلى ملاحظة أخرى تتعلق بالحفاظ على الطاقة: قيمها متنافية. لا يمكن امتصاص طاقة الضوء المنعكس بواسطة المادة. لذلك ، فإن الطاقة التي يمتصها السطح في شكل ضوء منكسر هي الطاقة المتبقية بعد حساب الضوء المنعكس.
نستخدم هذه النسبة ، ونحسب أولاً الجزء المنعكس كنسبة مئوية من طاقة الأشعة المنعكسة المنعكسة على السطح ، ثم جزء الضوء المنكسر مباشرة من المنعكس ، على النحو التالي:

float kS = calculateSpecularComponent(...); // /  float kD = 1.0 - kS; // /  

بهذه الطريقة نتعلم معاني كل من الأجزاء المنعكسة والمنكسرة بفضل قانون الحفاظ على الطاقة. مع هذا النهج ، لن يتجاوز الجزء المنكسر (المنتشر) ولا الجزء المنعكس 1.0 ، مما يضمن ألا تتجاوز طاقتهم الإجمالية قيمة طاقة الضوء الساقط ، والتي لم نتمكن من أخذها في الاعتبار في الدروس السابقة.

معادلة الانعكاس

ما سبق يقودنا إلى ما يسمى بمعادلة التقديم : معادلة معقدة اخترعها أشخاص أذكياء جدًا ، واليوم هي أفضل نموذج لمحاكاة الإضاءة. يتبع PBR بدقة نسخة أكثر تحديدًا من هذه المعادلة ، تُعرف باسم معادلة الانعكاس . لفهم PBR جيدًا ، من المهم أولاً أن يكون لديك فهم كامل لمعادلة الانعكاس:

$$

$$L_o (p، \ omega_o) = \ int \ limits_ \ Omega f_r (p، \ omega_i، \ omega_o) L_i (p، \ omega_i) n \ cdot \ omega_id \ omega_i$$

في البداية ، يبدو الأمر مخيفًا ، لكننا سنفككه بشكل تدريجي ، في أجزاء ، وسوف ترى مدى بطء الأمر في أن يصبح منطقياً. لفهم هذه المعادلة ، علينا أن نتعمق قليلاً في قياس الإشعاع. قياس الإشعاع هو علم قياس الإشعاع الكهرومغناطيسي (بما في ذلك الضوء المرئي). هناك العديد من كميات الإشعاع التي يمكننا استخدامها لقياس الإضاءة ، ولكننا لن نستخدم سوى واحدة تتعلق بمعادلة الانعكاس ، والمعروفة باسم إنارة الطاقة (إشعاع الإنجليزية) والمحددة هنا بالحرف L. EI ، تُستخدم لقياس مقدار أو شدة الضوء ، قادمة من اتجاه معين. EJ ، بدوره ، هو مزيج من العديد من الكميات المادية ، وحتى يكون من الأسهل علينا تخيلها ، سنركز على كل منها على حدة.

تدفق مشع

تدفق الإشعاع ( $$$\ Phi$ ) هي قوة الطاقة المنقولة بالضوء ، المقاسة بالواط. تتكون الطاقة الإجمالية للضوء من العديد من المصطلحات لأطوال موجية مختلفة ، كل منها يتوافق مع لونه الخاص من الطيف. يمكن تمثيل الطاقة المنبعثة من مصدر الضوء ، في هذه الحالة ، كدالة لكل هذه الأطوال الموجية. تشكل الأطوال الموجية من 390 نانومتر إلى 700 نانومتر الجزء المرئي من الطيف ، أي أن الإشعاع في هذا النطاق يمكن رؤيته بالعين البشرية. في الصورة أدناه يمكنك أن ترى قيم الطاقات لأطوال موجية مختلفة تشكل ضوء النهار:

يتوافق تدفق الإشعاع مع المنطقة تحت الرسم البياني لهذه الوظيفة لجميع أطوال الموجات. إن الاستخدام المباشر لأطوال موجات الضوء كمدخل في رسومات الكمبيوتر أمر غير عملي ، لذلك نلجأ إلى تمثيل مبسط لتدفق الإشعاع ، بدلاً من استخدام وظيفة لجميع أطوال الموجات ، ثلاثية الألوان ، المعروفة باسم RGB (أو ، كما نسميها عادة ، لون الإضاءة). يؤدي مثل هذا الرأي إلى فقدان بعض المعلومات ، ولكنه بشكل عام سيؤثر قليلاً على الصورة النهائية.

زاوية صلبة

الزاوية الصلبة تدل عليها $$$\ omega$ يعطينا حجم أو مساحة الشكل المسقطة على كرة الوحدة. يمكنك تخيله على أنه اتجاه به حجم:

تخيل أنك في وسط كرة وتبحث في اتجاه الشكل. سيكون حجم الصورة الظلية الناتجة زاوية صلبة.

شدة الإشعاع

تقيس قوة الإشعاع مقدار تدفق الإشعاع لكل زاوية صلبة ، أو قوة مصدر الضوء لكل وحدة مساحة محددة بالزاوية الصلبة. على سبيل المثال ، بالنسبة لمصدر ضوء شامل الاتجاهات ينبعث بالتساوي في جميع الاتجاهات ، فإن قوة الإشعاع تعني طاقة الضوء لكل منطقة محددة (زاوية صلبة):

تبدو المعادلة التي تصف قوة الإشعاع كما يلي:

$$

$$I = \ frac {d \ Phi} {d \ omega}$$

حيث I هو تدفق الإشعاع f لكل زاوية صلبة $$${d \ omega}$

بمعرفة تدفق الإشعاع والقوة والزاوية الصلبة ، يمكننا وصف معادلة سطوع الطاقة التي تصف إجمالي الطاقة المرصودة في المنطقة A ، مقيدة بالزاوية الصلبة O للضوء بالقوة $$$\ Phi$

$$

$$L = \ frac {d ^ 2 \ Phi} {dA d \ omega \ cos \ theta}$$

سطوع الطاقة هو كمية الإشعاع الضوئية للضوء في منطقة تعتمد على زاوية الضوء الساقط. $$$\ theta$ (الزاوية بين اتجاه الضوء والعادي على السطح) من خلال $$$cos \ theta$ : يكون الضوء أضعف عندما ينبعث على السطح ويكون أقوى عندما يكون عموديًا عليه. هذا مشابه لحساباتنا للضوء المنتشر في البرنامج التعليمي حول أساسيات الإضاءة منذ ذلك الحين $$$cos \ theta$ ليس أكثر من منتج عددي بين اتجاه الضوء والمتجه الطبيعي للسطح:

 float cosTheta = dot(lightDir, N); 

معادلة سطوع الطاقة مفيدة جدًا لنا ، لأنها تحتوي على معظم الكميات المادية التي تهمنا. إذا افترضنا أن الزاوية الصلبة ω والمنطقة A متناهي الصغر ، يمكننا استخدام EE لقياس تدفق شعاع واحد من الضوء لكل نقطة في الفضاء. سيسمح لنا هذا بحساب EI لشعاع ضوئي واحد يعمل على نقطة واحدة (جزء) ؛ نحن بالفعل نترجم الزاوية الصلبة $$$\ omega$ في اتجاه متجه $$$\ omega$ و $$$A$ إلى هذه النقطة $$$p$ . وبالتالي ، يمكننا استخدام EI مباشرة في تظليلنا لحساب مساهمة شعاع ضوء واحد لكل جزء.

في الواقع ، عندما يتعلق الأمر بـ EE ، فإننا عادةً ما نهتم بجميع حوادث الضوء الواردة في النقطة p ، والتي تمثل مجموع EE بالكامل ، والمعروفة باسم الإشعاع. بمعرفة EI والإشعاع ، يمكننا العودة إلى معادلة الانعكاس:

$$

$$L_o (p، \ omega_o) = \ int \ limits_ \ Omega f_r (p، \ omega_i، \ omega_o) L_i (p، \ omega_i) n \ cdot \ omega_id \ omega_i$$

الآن نحن نعلم ذلك $$$L$ في معادلة التجسيد هو EI لبعض النقاط على السطح p وبعض الزاوية الصلبة الصغيرة بلا حدود للضوء الوارد $$$\ omega_i$ ، والتي يمكن اعتبارها ناقلات اتجاه الإدخال $$$\ omega_i$ . تذكر أن الطاقة مضروبة في $$$cos \ theta$ - الزاوية بين اتجاه حدوث الضوء والعادي على السطح ، والتي يتم التعبير عنها في معادلة الانعكاس بواسطة المنتج $$$n \ cdot \ omega_i$ . تحسب معادلة الانعكاس مجموع الذكاء العاطفي المنعكس $$$L_o (p، \ omega_o)$ النقاط $$$p$ نحو $$$ω_o$ ، وهو الاتجاه الصادر للمراقب. وإلا: $$$L_o$ يقيس الإشعاع المنعكس للنقطة $$$p$ إذا تم عرضها من $$$\ omega_o$ .

نظرًا لأن معادلة الانعكاس تستند إلى الإشعاع ، وهو مجموع كل الإشعاع الوارد ، فإننا نقيس الضوء ليس فقط من اتجاه ضوء وارد واحد ، ولكن من جميع اتجاهات الضوء الواردة داخل نصف الكرة الأرضية $$$\ أوميغا$ تركزت في $$$p$ . يمكن وصفه بأنه نصف كرة موجهة على طول السطح العادي $$$n$ :

من أجل حساب مجموع جميع القيم داخل المنطقة ، أو ، في حالة نصف الكرة الأرضية ، الحجم ، ندمج المعادلة في جميع الاتجاهات الواردة $$$d \ omega_i$ داخل نصف الكرة الأرضية $$$\ أوميغا$ . نظرًا لعدم وجود حل تحليلي لكل من معادلة التقديم ومعادلة الانعكاس ، فسنحل المعادلة العددية. هذا يعني أننا سنحصل على نتائج لخطوات منفصلة صغيرة لمعادلة انعكاس نصف الكرة الأرضية $$$\ أوميغا$ وحسابها فوق حجم الخطوة. وهذا ما يسمى مجموع ريمان ، والذي يمكننا تمثيله تقريبًا بالكود التالي:

 int steps = 100; float sum = 0.0f; vec3 P = ...; vec3 Wo = ...; vec3 N = ...; float dW = 1.0f / steps; for(int i = 0; i < steps; ++i) { vec3 Wi = getNextIncomingLightDir(i); sum += Fr(P, Wi, Wo) * L(P, Wi) * dot(N, Wi) * dW; } 

يمكن اعتبار dW لكل خطوة منفصلة على أنها $$$d \ omega_i$ في معادلة الانعكاس. رياضيا $$$d \ omega_i$ هو التفاضل الذي نحسب به التكامل ، وعلى الرغم من أنه ليس مثل dW في الكود (نظرًا لأن هذه خطوة منفصلة من مجموع Riemann) ، يمكننا اعتبارها على هذا النحو لسهولة الحساب. ضع في اعتبارك أن استخدام الخطوات المنفصلة سيمنحنا دائمًا مبلغًا تقريبيًا ، وليس القيمة الدقيقة للتكامل. سيلاحظ القارئ اليقظ أنه يمكننا زيادة دقة مجموع ريمان عن طريق زيادة عدد الخطوات.

تجمع معادلة الانعكاس الإشعاع لجميع اتجاهات الضوء الواردة $$$\ omega_i$ نصف الكرة الأرضية $$$\ أوميغا$ يصل إلى النقطة $$$p$ ويعيد مقدار الضوء المنعكس $$$L_o$ تجاه المشاهد. يمكن أن يأتي الإشعاع الوارد من مصادر الضوء التي نعرفها بالفعل ، أو من الخرائط البيئية التي تحدد EI لكل اتجاه وارد ، والذي سنتحدث عنه في البرنامج التعليمي IBL.

الآن المجهول الوحيد على اليسار هو الرمز $$$f_r$ ، تُعرف باسم وظيفة BRDF أو دالة الانعكاس ثنائية الشعاع ، والتي تقيس (أو تزن) قيمة الإشعاع الوارد بناءً على خصائص المواد السطحية.

BRDF

BRDF هي وظيفة تقبل اتجاه الضوء الساقط. $$$\ omega_i$ توجيه للمراقب $$$\ omega_o$ عادي على السطح $$$n$ والمعلمة $$$a$ وهو خشونة السطح. يقارب BRDF مقدار كل شعاع ضوء فردي $$$\ omega_i$ يساهم في الضوء المنعكس النهائي لسطح معتم ، مع مراعاة خصائص مادته. على سبيل المثال ، إذا كان السطح أملسًا تمامًا (مثل المرآة تقريبًا) ، فستقوم وظيفة BRDF بإرجاع 0.0 لجميع أشعة الضوء الواردة $$$\ omega_i$ باستثناء زاوية لها نفس زاوية الحزمة (بعد الانعكاس) $$$\ omega_o$ التي سترجع الدالة 1.0.

يقوم BRDF بتقريب الخصائص الانعكاسية والانكسارية للمادة بناءً على نظرية الوجوه الدقيقة المذكورة سابقًا. من أجل أن يكون BRDF مقبولًا جسديًا ، يجب أن يطيع قانون الحفاظ على الطاقة ، أي أن الطاقة الإجمالية للضوء المنعكس يجب ألا تتجاوز أبدًا طاقة الضوء الساقط. من الناحية الفنية ، يعتبر نموذج Blinn-Fong من BRDF يقبل نفسه $$$\ omega_i$ و $$$\ omega_o$ عند المدخل. ومع ذلك ، لا يعتبر نموذج Blinn-Fong صحيحًا جسديًا ، لأنه لا يضمن الامتثال لقانون الحفاظ على الطاقة. هناك العديد من وحدات BRDFs الصحيحة ماديًا لتقريب استجابة السطح للإضاءة. ومع ذلك ، تستخدم جميع خطوط الأنابيب في الوقت الفعلي تقريبًا BRDF ، والمعروفة باسم Cook-Torrance BRDF .

يحتوي Cook-Torrens BRDF على جزء منتشر ومرآة:

$$

$$f_r = k_df_ {lambert} + k_sf_ {cook - torrance}$$

هنا $$$k_d$ - جزء من انكسار الطاقة الضوئية الواردة ، $$$k_s$ - ينعكس. الطرف الأيسر من BRDF يحتوي على الجزء المنتشر من المعادلة ، المشار إليه هنا كـ $$$f_ {lambert}$ . هذا ما يسمى تشتت لامبرت. إنه مشابه لما استخدمناه للإضاءة المنتشرة ، وهو ثابت:

$$

$$f_ {lambert} = \ frac {c} {\ pi}$$

أين $$$c$ - البياض أو لون السطح (قوام السطح المنتشر). القسمة على $$$\ pi$ اللازمة لتطبيع الضوء المتناثر ، حيث يتم ضرب BRDF الذي يحتوي على جزء لا يتجزأ من قبل $$$\ pi$ (سنصل إلى هذا في البرنامج التعليمي IBL).

قد تتفاجأ من كيفية تشابه هذا التشتت اللامبرتي مع التعبير عن الإضاءة المنتشرة التي استخدمناها من قبل: لون السطح مضروبًا بالمنتج القياسي بين السطح الطبيعي واتجاه الضوء. لا يزال منتج العدد موجودًا ، ولكن يتم استنتاجه من BRDF ، منذ أن كنا $$$n \ cdot \ omega_i$ في جزء لا يتجزأ $$$L_o$ .

هناك معادلات مختلفة للجزء المنتشر من BRDF التي تبدو أكثر واقعية ، لكنها أكثر تكلفة من حيث الأداء. بالإضافة إلى ذلك ، كما خلصت ألعاب Epic Games: تشتت لامبرتن كافٍ لمعظم أغراض العرض في الوقت الفعلي.

تم تحسين جزء المرآة من Cook-Torrens BRDF بشكل طفيف ويوصف بأنه:

$$

$$f_ {cook - torrance} = \ frac {DFG} {4 (\ omega_o \ cdot n) (\ omega_i \ cdot n)}$$

يتكون من ثلاث وظائف ومعامل توحيد في المقام. يمثل كل حرف من الأحرف D و F و G نوعًا معينًا من الوظائف يقارب جزءًا معينًا من الخصائص العاكسة للسطح. تُعرف باسم دالة التوزيع العادية (NDF) ومعادلة فرينل ودالة الهندسة:

• دالة التوزيع الطبيعي: تقارب عدد الواجهات الدقيقة السطحية الموجهة على طول الناقل المتوسط ​​، اعتمادًا على خشونة السطح ؛ هذه هي الوظيفة الرئيسية تقريب الوجوه الصغيرة.
• دالة الهندسة: تصف خاصية التظليل الذاتي للوجوه الدقيقة. عندما يكون السطح خشنًا إلى حد ما ، يمكن أن تتداخل بعض الوجوه الدقيقة للسطح مع بعضها البعض ، مما يقلل من كمية الضوء المنعكسة على السطح.
• معادلة فرينل: تصف معامل الانعكاس السطحي بزوايا مختلفة.

كل من هذه الوظائف هي تقريب لمعادلها المادي ، وبالنسبة لهم هناك العديد من التطبيقات التي تهدف إلى تقريب أكثر دقة للنموذج المادي الأساسي ؛ بعضها يعطي نتائج أكثر واقعية ، والبعض الآخر أكثر فعالية من حيث الأداء. قام Brian Caris من Epic Games بالكثير من الأبحاث حول الأنواع المختلفة للتقريب ، والتي يمكنك معرفة المزيد عنها هنا . سنستخدم نفس الوظائف الموجودة في Unreal Engine 4 من Epic Games ، وهي: Trowbridge-Reitz GGX for D و Fresnel-Schlick لـ F و Smith's Schlick-GGX for G.

دالة التوزيع الطبيعي

تقارب دالة التوزيع العادية D إحصائيًا المساحة السطحية النسبية للوجوه الدقيقة الموجهة بدقة على طول المتجه الوسيط $$$h$ . هناك العديد من NDFs التي تحدد التقريب الإحصائي للمحاذاة الإجمالية للوجوه الدقيقة مع مراعاة بعض معلمات الخشونة. سنستخدم واحدًا يعرف باسم Trowbridge-Reitz GGX:

$$

$$NDF_ {GGXTR} (n، h، \ alpha) = \ frac {\ alpha ^ 2} {\ pi ((n \ cdot h) ^ 2 (\ alpha ^ 2−1) +1) ^ 2}$$

هنا $$$h$ هو الوسيط المتجه ، $$$\ alpha$ - قيمة خشونة السطح. إذا اخترنا $$$h$ كمتوسط ​​متوسط ​​بين العادي إلى السطح واتجاه الضوء ، ثم تغيير معلمة الخشونة ، نحصل على الصورة التالية:

عندما تكون الخشونة صغيرة (أي السطح أملس) ، تتركز الوجوه الدقيقة الموجهة في اتجاه الناقل المتوسط ​​في نصف قطر صغير. بسبب هذا التركيز العالي ، يعطي NDF بقعة مشرقة جدًا. على سطح خشن ، حيث يتم توجيه الوجوه الدقيقة في اتجاهات أكثر عشوائية ، ستجد عددًا أكبر بكثير من الوجوه الدقيقة الموجهة باتجاه المتجه الوسيط $$$h$ ولكن تقع في دائرة نصف قطرها أكبر ، مما يجعل لون التركيز أكثر رمادية.

في كود GLSL ، ستبدو وظيفة التوزيع الطبيعي Trowbridge-Reitz GGX كما يلي:

 float DistributionGGX(vec3 N, vec3 H, float a) { float a2 = a*a; float NdotH = max(dot(N, H), 0.0); float NdotH2 = NdotH*NdotH; float nom = a2; float denom = (NdotH2 * (a2 - 1.0) + 1.0); denom = PI * denom * denom; return nom / denom; } 

دالة هندسية

تقارب وظيفة الهندسة إحصائيًا المساحة السطحية النسبية ، حيث تتداخل مخالفاتها المجهرية ، مما يمنع أشعة الضوء من الاختراق.

كما هو الحال في NDF ، تقبل وظيفة الهندسة معامل خشونة السطح كمدخل ، وهو ما يعني في هذه الحالة ما يلي: سيكون للأسطح الأكثر خشونة احتمالية أعلى لتظليل الوجوه الدقيقة. وظيفة الهندسة التي سنستخدمها هي مزيج من تقريب GGX و Schlick-Beckmann ، والمعروف باسم Schlick-GGX:

$$

$$G_ {SchlickGGX} (n، v، k) = \ frac {n \ cdot v} {(n \ cdot v) (1 - k) + k}$$

هنا $$$k$ هي إعادة تصميم $$$\ alpha$ اعتمادًا على ما إذا كنا نستخدم وظيفة الهندسة للإضاءة المباشرة أو إضاءة IBL:

$$

$$k_ {direct} = \ frac {(\ alpha + 1) ^ 2} {8}$$

$$

$$k_ {IBL} = \ frac {\ alpha ^ 2} {2}$$

يرجى ملاحظة أن القيمة $$$\ alpha$ قد تختلف حسب كيفية ترجمة محركك للخشونة $$$\ alpha$ . سنناقش في الدروس التالية بالتفصيل كيف وأين تصبح إعادة التعيين هذه ذات صلة.

من أجل تقريب الهندسة بشكل فعال ، نحتاج أن نأخذ في الاعتبار كل من اتجاه العرض (الهندسة المتداخلة) ومتجه اتجاه الضوء (التظليل الذاتي للهندسة). يمكننا النظر في الحالتين باستخدام طريقة سميث :

$$

$$G (n، v، l، k) = G_ {sub} (n، v، k) G_ {sub} (n، l، k)$$

استخدام طريقة سميث مع Schlick-GGX كـ $$$G_ {sub}$ يعطي الصورة التالية بخشونة مختلفة R:

دالة الهندسة هي عامل بين [0.0 ، 1.0] ، حيث الأبيض (أو 1.0) يعني عدم تظليل الوجوه الدقيقة ، والأسود (أو 0.0) يعني تظليل كامل للوجوه الدقيقة.

في GLSL ، يتم تحويل دالة الهندسة إلى التعليمات البرمجية التالية:

 float GeometrySchlickGGX(float NdotV, float k) { float nom = NdotV; float denom = NdotV * (1.0 - k) + k; return nom / denom; } float GeometrySmith(vec3 N, vec3 V, vec3 L, float k) { float NdotV = max(dot(N, V), 0.0); float NdotL = max(dot(N, L), 0.0); float ggx1 = GeometrySchlickGGX(NdotV, k); float ggx2 = GeometrySchlickGGX(NdotL, k); return ggx1 * ggx2; } 

معادلة فرينل

تصف معادلة فريسنل نسبة الضوء المنعكس والمنكسر ، والتي تعتمد على الزاوية التي ننظر فيها إلى السطح. عندما يصطدم الضوء بسطح ما ، فإن معادلة فريسنل تعطينا النسبة المئوية للضوء المنعكس بناءً على الزاوية التي نرى عندها هذا السطح. من هذه النسبة من الانعكاس وقانون الحفاظ على الطاقة ، يمكننا الحصول مباشرة على الجزء المنكسر من الضوء ، والذي سيكون مساوياً للطاقة المتبقية.

لكل سطح أو مادة مستوى من الانعكاس الأساسي ، يتم ملاحظته عند النظر إلى السطح مباشرة ، ولكن إذا نظرت إلى السطح بزاوية ، تصبح جميع الانعكاسات أكثر وضوحًا. يمكنك التحقق من ذلك بنفسك من خلال النظر إلى طاولتك الخشبية أو المعدنية على الأرجح بشكل عمودي أولاً ثم بزاوية قريبة من 90 درجة. سترى أن الانعكاسات تصبح ملحوظة أكثر بكثير. تعكس جميع الأسطح ، نظريًا ، الضوء تمامًا عند عرضها منه بزاوية مثالية تبلغ 90 درجة. يدعى هذا التأثير فريسنل ويتم وصفه بواسطة معادلة فريسنل .

معادلة فريسنل معقدة للغاية ، ولكن لحسن الحظ ، يمكن تبسيطها باستخدام تقريب فريسنيل-شليك :

$$

$$F_ {Schlick} (h، v، F_0) = F_0 + (1 - F_0) (1− (h \ cdot v)) ^ 5$$

$$$F_0$ يمثل الانعكاس الأساسي للسطح ، الذي نحسبه باستخدام شيء يسمى مؤشرات الانكسار أو IORs (مؤشرات الانكسار) ، وكما ترى على سطح الكرة ، كلما اقترب اتجاه العرض من حدود المجال المرئي (الزاوية بين اتجاه العرض والوسط 90 ), , , :

, . , - . (), , . , ( $$$F_0$ ) ( 0 , ) -, , .

. , , :

: 0.17, , , ( ) 0.5 1.0. , “”, $$$F_0$ RGB ( ).

, metallic workflow: , (metalness), , .

: , ; , . , 0.0 1.0. - , , , . , .

$$$F_0$ , , - , , . :

 vec3 F0 = vec3(0.04); F0 = mix(F0, surfaceColor.rgb, metalness); 

, . , $$$F_0$ . 0.04 . , , , F0 . , , .

- :

 vec3 fresnelSchlick(float cosTheta, vec3 F0) { return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0); } 

cosTheta .

-

BRDF - :

$$

$$L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi}+k_s\frac{DFG}{4(\omega_o\cdot n)(\omega_i \cdot n)}) L_i(p, \omega_i)n\cdot \omega_i d\omega_i$$

. , , F . $$$k_s$ , , $$$k_s$ . , :

$$

$$L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi}+\frac{DFG}{4(\omega_o\cdot n)(\omega_i \cdot n)}) L_i(p, \omega_i)n\cdot \omega_i d\omega_i$$

, PBR. , , . , , .

PBR

, PBR, , , PBR. , PBR, . , : , .

, PBR, :

: , . , . , ; .

: , , . , , .

: . , PBR-, , : .

: , . . , . PBR- , , (1.0 — ) .

AO (ambient occlusion) : AO . , , . AO , . . , 3D-.

. PBR, , . , PBR, PBR-, , , .

• Background: Physics and Math of Shading by Naty Hoffmann: , , ; PBR, must-read .
• Real shading in Unreal Engine 4 : PBR, Epic Games Unreal Engine 4. PBR, , .
• Marmoset: PBR Theory : PBR. , , , .
• Coding Labs: Physically based rendering : , PBR.
• Coding Labs: Physically Based Rendering — Cook–Torrance : BRDF -
• Wolfire Games — Physically based rendering : PBR Lukas Orsvärn.
• [SH17C] Physically Based Shading : shadertoy (: ) Krzysztof Narkowi, PBR.