
ربما يكون لديك سؤال معقول: لماذا؟
من وجهة نظر براغماتية ليست هناك حاجة) يمكنك دائمًا استخدام التنغستن الشرطي ، وإذا كنت بحاجة إلى القيام بذلك في الثعبان ، فاستخدم وحدات خاصة ليس من الصعب إتقانها.
ولكن إذا تم تكليفك فجأة بمثل هذه المهمة أو كنت تحب البرمجة حقًا ، مثلي ، فستكون لديك ساعات مثيرة - وأحيانًا ليست شديدة - لكتابة برنامج وتصحيحه)
عند كتابة هذه التحفة الفنية ، نحتاج حقًا إلى تصحيح الأخطاء خطوة بخطوة ، لذا يرجى تنزيل PyCharm أو VS أو أي شيء آخر بهذه الميزة. لبناء الجداول ، فإن عدم وجود هذه الوظيفة ليس بالغ الأهمية ، ولكن للتآمر ...
لذا ، ماذا سيكون برنامجي. عند الإدخال ، سيستغرق الأمر ثلاث قيم: بداية ونهاية المقطع الذي نريد أن نرى وظيفتنا والخطوة التي سنتحرك بها. بعد ذلك ، سنرسم جدولًا لقيم الدوال في كل نقطة من نطاق القيم المحدد بواسطة بيانات الإدخال. حسنًا ، سنرسم الرسم البياني للدالة نفسها مع المحور ص المتحرك.
لذا دعنا نذهببادئ ذي بدء ، سأعلن عن العديد من الوظائف التي سننظر في قيمها. سآخذ بشكل بسيط للغاية
from math import sqrt def y1(x): return x**3 - 2*x**2 + 4*x - 8 def y2(x): return 1 - 1/x**2 def y3(x): return sqrt(abs(y1(x)*y2(x)))
الآن لدينا ثلاث وظائف ، اثنتان منها لها نقطة فاصل. من وحدة الرياضيات ، التي تقوم بتخزين جميع الكعكات الرياضية (بما في ذلك التمامات ، المنحنيات ، وعلم المثلثات الأخرى) ، نستورد sqrt ، أي الجذر التربيعي. نحتاجها لقراءة الدالة y3.
بعد ذلك ، نحتاج إلى قراءة نطاق الوظيفة بواسطة x والخطوة التي نمر بها عبر هذا النطاق. لهذا ، سأستخدم الخريطة.
كمعلمة أولى ، تأخذ هذه الوظيفة بعض الوظائف التي تحول بطريقة ما البيانات التي نحتاجها ، وكوسيطة ثانية ، نوع من ورقة البيانات التي نحتاج إلى معالجتها
from_x, to_x, pace_x = map(float, input("Enter the first and the last"\ " x-coordinates and a pace dividing them by a"\ " space:").split())
نقرأ القيم الثلاث التي تم إدخالها من خلال مسافة ، ونقسمها إلى عناصر بمسافة (باستخدام طريقة الانقسام ، التي ، عند استدعاؤها بدون معلمات ، ستقسم السلسلة التي تحددها بمسافات تلقائيًا). البيانات التي تم إدخالها باستخدام الإدخال () ستكون بشكل افتراضي من نوع str ، أي سلسلة ، لذلك لن يكون لدينا أي أخطاء هنا.
نظرًا لأن أرقام حدود النطاق يمكن أن تكون كسرية ، فإننا نقوم بتحويل كل عنصر من المصفوفة الناتجة إلى رقم حقيقي باستخدام الدالة float.
لاحظ أنه يتم الإعلان عن المتغيرات دون تحديد نوع البيانات. يتم تحديده تلقائيًا (نوع بيانات القيمة التي تحاول تعيينها للمتغير) ، أو باستخدام str ، int ، float ، إلخ. يتم تعيينها يدويًا بواسطة المتغيرات ، مع تطبيق نفس الوظائف على القيم. يمكن أن يحتوي المتغير نفسه على نوع بيانات مختلف طوال البرنامج - ما عليك سوى تعيين قيمة جديدة له بنوع بيانات مختلف.
على سبيل المثال
auxiliary_variable = ""
دعنا نعود إلى برنامجنا. نحتاج إلى التحقق من صحة البيانات المدخلة.
يجب أن يطبع البرنامج أن البيانات المدخلة غير صحيحة إذا:
- الخطوة هي 0
- الحد الأدنى للنطاق أكبر من النطاق العلوي ، والخطوة إيجابية (أي ، لدينا تطور حسابي للنموذج xn = from_x + speed_x * (n - 1) ، حيث from_x> to_x . منذ speed_x> 0 ، سيزداد هذا التقدم ونحن لا تحصل على to_x )
- الحد الأدنى للنطاق أقل من الحد العلوي ، والخطوة سلبية (تفكير مشابه)
- الرسوم البيانية التي تتكون من نقطة واحدة ليست غنية بالمعلومات ، لذلك يجب أن يحتوي الجزء الذي نقوم بإنشاء الدالة عليه على قيمتين على الأقل
نقوم بصياغة هذه الشروط في الكود. من الواضح أن العنصر الأول سهل الضبط. يمكن دمج الثاني والثالث في واحد ، إذا لاحظت أن علامة الفرق بين الأول (from_x) والأخير (to_x) يجب أن تتزامن مع علامة الخطوة. حسنًا ، النقطة الرابعة ليست معقدة أيضًا: يجب ألا يقل معامل الفرق بين القيمتين الأولى والأخيرة عن وحدة الخطوة.
بسبب الوحدة ، قد يكون لدينا موقف لا تتزامن فيه علامات الاختلاف والخطوة ، ولكن الشرط الثاني سيقطع هذه الحالات ، لذلك الشرط صحيح.
ونتيجة لذلك ، ستبدو هذه الشروط الثلاثة كما يلي:
if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x):
ننتقل مباشرة إلى الجدول. لسهولة تصحيح الأخطاء ، سأقوم بإنشاء العديد من المتغيرات بأسماء التحدث التي ستكون مسؤولة عن دقة الأرقام ، وعدد المسافات قبل الرقم ، وعدد المسافات بعد الرقم ، وما إلى ذلك.
dials_precision = "%10.6g"
إذن ما الذي يحدث هنا؟

dials_precision = "%10.6g"
في هذا الخط أضبط دقة الرقم. 10 أحرف كحد أقصى للرقم الصحيح و 6 أحرف للجزء الكسري. إذا كانت لدينا قيمة كبيرة جدًا لهذا النطاق ، فستظهر جميع أنواع
e-15s أو شيء مماثل.
spaces_in_the_title = int((int(dials_precision[1:3])) / 2)
dials_precision عبارة عن سلسلة ، لذا يمكننا أخذ شريحة من هذه السلسلة ، أي نوع من السلسلة الفرعية. في هذه الحالة ، نحتاج إلى الحصول على الرقم 10 ، لذلك نأخذ الأحرف بمؤشرين 1 و 2 ، ونحول هذه السلسلة الفرعية إلى نوع بيانات صحيح ، ونقسمها على اثنين ونقربها لأسفل.
نحتاج إلى هذا المتغير بحيث تتمركز النقوش في عنوان الجدول على الخلية
length_of_table_lower_bound = (int(dials_precision[1:3]) + 2) * 4 + 5
كما يوحي الاسم ، هذا المتغير مسؤول عن طول الحدود الدنيا لخلايا جدول قيم الدالة. في المجموع ، يشغل الرقم 10 مواضع ، مما يعني أن العمود لا يمكن أن يكون عرضه أقل من 10. عندما نحصل على أرقام بتنسيق e-15 (الموضح أعلاه) ، تأخذ القيمة 11-12 موضعًا. لذلك ، إلى 10 نضيف إشارة أخرى.
4 مسؤول عن عدد الأعمدة (x ، y1 ، y2 ، y3) ، و 5 هو عدد الأحرف التي تحدد الخلية في صف.
يبدو أن باقي المتغيرات بديهية ، لذلك دعنا ننتقل إلى طباعة اللوحة
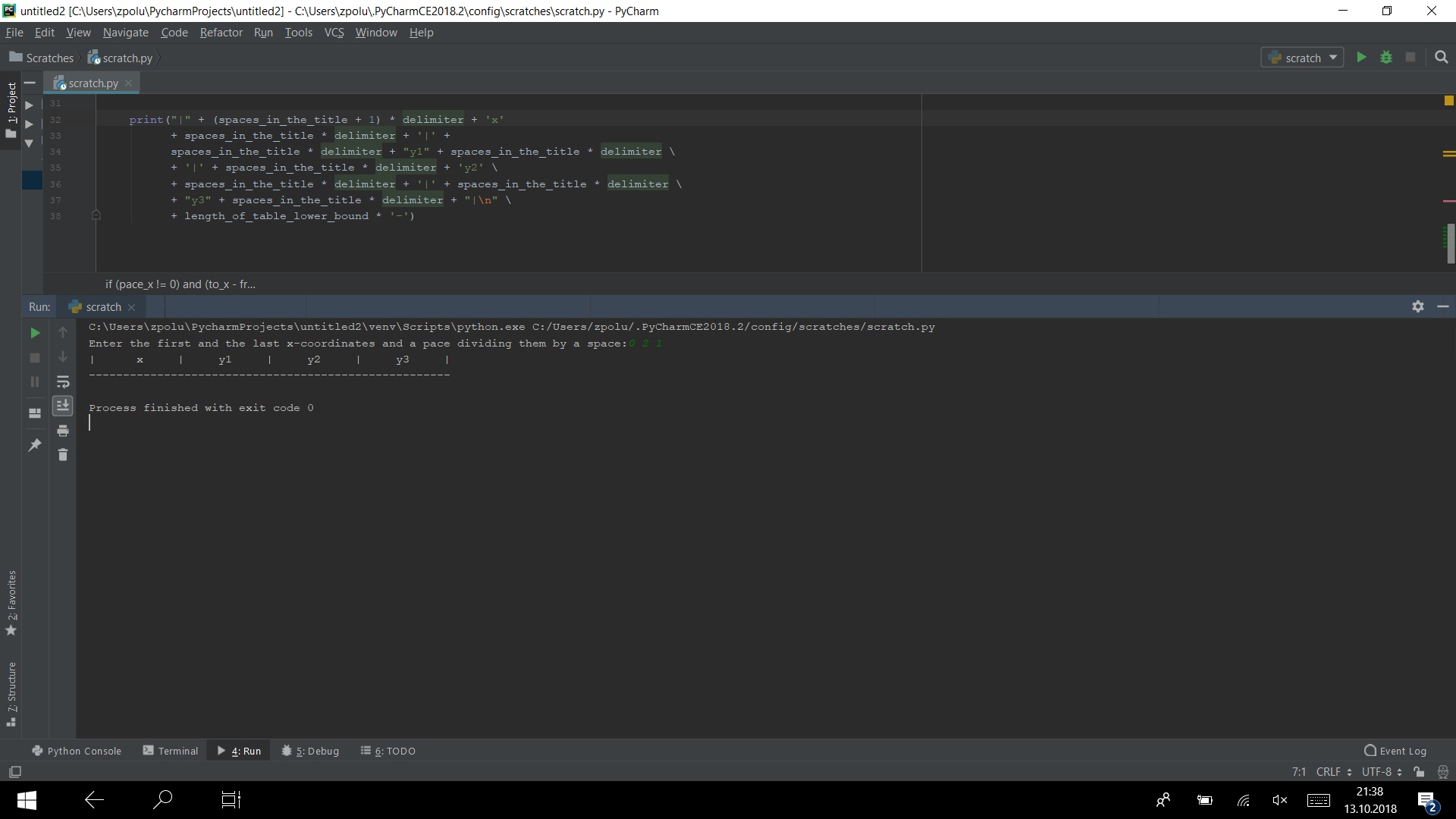
print("|" + (spaces_in_the_title + 1) * delimiter + 'x' + spaces_in_the_title * delimiter + '|' + spaces_in_the_title * delimiter + "y1" +\ spaces_in_the_title* delimiter\ + '|' + spaces_in_the_title * delimiter + 'y2'\ + spaces_in_the_title * delimiter + '|' +\ spaces_in_the_title * delimiter\ + "y3" + spaces_in_the_title * delimiter + "|\n"\ + length_of_table_lower_bound * '-')
إذا قمنا بتوصيل جميع التعليمات البرمجية التي كتبناها بالفعل ، فسوف نرى في وحدة التحكم هذا:
الآن نحن بحاجة إلى طباعة القيم نفسها. للقيام بذلك ، تحتاج إلى حلقة. نظرًا لأن البيانات التي تم إدخالها قد تكون كسرية ، فلن يعمل استخدام
النطاق ، لذلك سأستخدم حلقة منتظمة.
نظرًا لأنه يمكن أن يكون لدينا تسلسل تنازلي لـ Xs وتسلسل متزايد ، يجب تعيين شروط الدورة بحيث يتم أخذ كل من هذين الخيارين في الاعتبار. لدينا متغير تم إنشاؤه سابقًا يقوم بتخزين الإجابة حول طبيعة التسلسل في شكل 0 أو 1. لذلك ، يكفي النظر في حالتين وتحديد الشرط المناسب لكل منهما
while(is_sequence_decreasing and x_copy >= to_x) or\ (not is_sequence_decreasing and x_copy <= to_x):
نظرًا لأن الرسم البياني نحتاج إلى الحد الأدنى والحد الأقصى للرسم البياني y1 ، الذي سنرسمه ، فإننا نقدم متغيرات خاصة ستكون مسؤولة عن الحد الأدنى والحد الأقصى
y1_cur_value = y1(x_copy) min_y1_value = (min_y1_value > y1_cur_value) * y1_cur_value + \ (min_y1_value <= y1_cur_value) * min_y1_value max_y1_value = (max_y1_value < y1_cur_value) * y1_cur_value + \ (max_y1_value >= y1_cur_value) * max_y1_value negative_value_exists += y1_cur_value < 0
يكرر البناء ، في جوهره ، بناء
إذا: ... وإلا: ... ، فقط من خلال التفاوتات المنطقية. تخزن
y1_cur_value القيمة الحالية للدالة. لقد قمت بإنشاء متغير حتى لا أستدعي وظيفة باستمرار عندما تكون قيمتها عند الحاجة.
سنحتاج أيضًا إلى وجود قيم سلبية للتآمر.

الآن قم بطباعة القيم مباشرة. أريد أن يكون كل شيء جميلًا ومتمركزًا في كل خلية ، لذا يتعين علي معالجة كل قيمة يدويًا للتحقق من طول الرقم وتحديد عدد المسافات اعتمادًا عليه لمحاذاة القيمة.
ملاحظة
حرفيا توسيط الرقم لن يعمل. المتغير المسؤول عن الدقة لديه المعلمة g. يقول أن عددًا معينًا من المواقف للأرقام محجوز لرقم (في حالتنا ، 10 افتراضيًا). إذا لم يتم طلب 10 أرقام ، فسيتم تحديد المواضع الفارغة على يسار المواضع المعبأة. لذلك ، يمكننا توسيط صف من 10 مواضع فقط.
aux_x = dials_precision % x_copy aux = len(aux_x) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_x) == int(dials_precision[1:3]) + 1 print('|' + delimiter * aux + aux_x + delimiter * (aux - aux_2) + '|', end='')
aux_x - سلسلة تم عرضها بالفعل على طريقة عرض بدقة معينة. نحتاج الآن إلى التحقق من طول الرقم وتحديد عدد المسافات المطلوبة. نظرًا لعدم الحاجة إلى أكثر من مساحة واحدة على كل جانب ، فإن متغيرات
bool eva مثالية كحارس لعدد هذه المساحات نفسها. يلتقط
aux_2 الحالة عندما يكون طول الرقم 11.
نفعل أيضا لقيم ثلاث وظائف
aux_y1 = dials_precision % y1_cur_value aux = len(aux_y1) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y1) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y1 + delimiter * (aux - aux_2) + '|', end='') if (x_copy != 0): aux_y2 = dials_precision % y2(x_copy) aux = len(aux_y2) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y2) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y2 + delimiter * (aux - aux_2) + '|', end='') aux_y3 = dials_precision % y3(x_copy) aux = len(aux_y3) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y3) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y3 + delimiter * (aux - aux_2) + \ "|\n" + length_of_table_lower_bound * '-') else: print((spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + '|' \ + (spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + "|\n" \ + length_of_table_lower_bound * '-') x_copy += pace_x
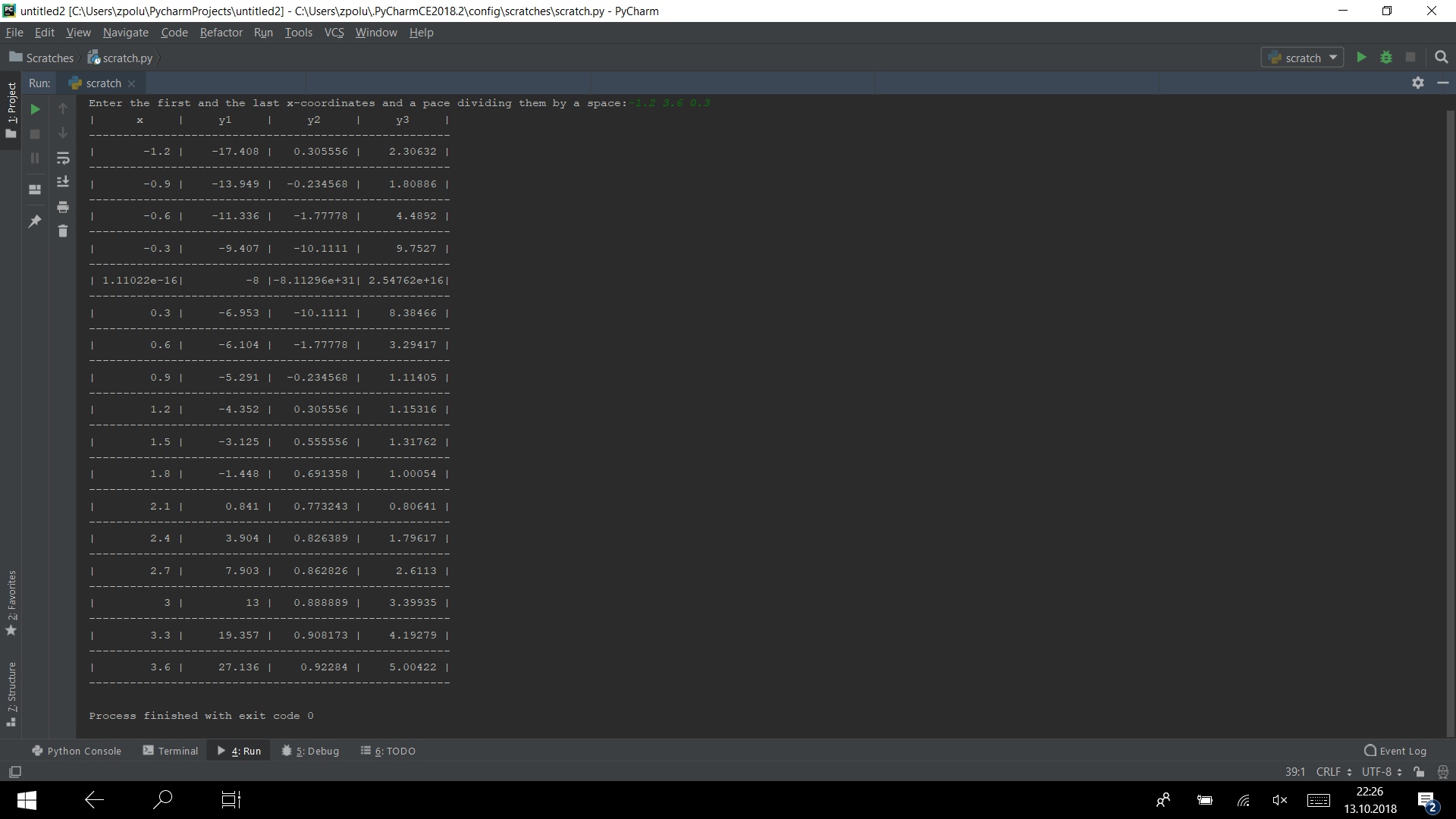
كما قلت في البداية ، تحتوي الدالتان الثانية والثالثة على نقاط كسر - كلا الدالتين غير موجودتين عند النقطة x = 0. لذلك ، نحتاج أيضًا إلى التقاط هذه الحالات.
حسنًا ، لا تنس زيادة قيمة x الحالية حتى لا نحصل على دورة لا نهاية لها.
دعونا نجمع كل الكود في برنامج واحد ونقوم بتشغيله ، على سبيل المثال ، في الاختبار -1.2 3.6 0.3
from math import sqrt def y1(x): return x**3 - 2*x**2 + 4*x - 8 def y2(x): return 1 - 1/x**2 def y3(x): return sqrt(abs(y1(x)*y2(x))) from_x, to_x, pace_x = map(float, input("Enter the first and the last"\ " x-coordinates and a pace dividing them by a"\ " space:").split()) if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x): dials_precision = "%10.6g"
في الجزء الثاني من هذا الخلق ، سنقوم ببناء الرسوم البيانية
 يتبع ...
يتبع ...