
نستمر في التعرف على لغة برمجة جوليا الصغيرة ، ولكنها جميلة بشكل لا يصدق. لقد انتهى الإصدار التجريبي لمدة ست سنوات أخيرًا ، لذا لا يمكنك الآن أن تخاف من تغييرات بناء الجملة. وبينما يناقش الجميع ما إذا كان من الجيد أو السيئ البدء في الفهرسة من واحدة ، فإن المجتمع المهتاج يعبث بنشاط: المكتبات الجديدة تظهر ، ويتم تحديث المكتبات القديمة ، وتبدأ المشاريع الجادة ، ويقوم الطلاب بتدريس هذه اللغة بنشاط في الجامعات. لذا دعونا لا نتخلف عن الركب! نحن نصنع الشاي أقوى ، لأننا سنبرمج هذه الليلة!
التحضير للعمل
هنا هناك مراجعة صغيرة باللغة الروسية ، يوجد أيضًا في المحور معرفة باللغة وتعليمات التثبيت . مرة أخرى ، بالتركيز على الحاجة إلى Windows Management Framework ، ستكون هناك مشاكل في تنزيل الحزم.
بعد الترقية ، يتضمن JuliaPRO الآن Juno فقط. لكني شخصياً أحب Jupyter أكثر : لم تكن هناك مشاكل معه على الكمبيوتر المحمول ، بالإضافة إلى أنه ملائم للعمل في المتصفح وإنشاء ملاحظات وصيغ على الفور ، بشكل عام ، مثالية لإنشاء التقارير أو الشرائح أو الكتيبات.
هناك العديد من الحزم لجوليا ، يتم تضمين أنجحها في المؤامرات كخلفية. Plots.jl - metalanguage of charting: أي واجهة لمختلف مكتبات الرسوم البيانية. وبالتالي ، فإن Plots.jl الواقع يفسر Plots.jl ثم ينشئ الرسوم البيانية باستخدام نوع من مكتبة الرسم البياني. تسمى مكتبات رسومات الخلفية هذه الخلفية. أفضل جزء هو أنه يمكنك استخدام العديد من مكتبات الرسومات المختلفة مع بناء جملة Plots.jl ، وسنرى أيضًا أن Plots.jl يضيف ميزات جديدة لكل من هذه المكتبات!
قم بتثبيت حزم الرسوملتثبيت الحزم ، قم بتشغيل الأوامر في REPL أو Juno أو Jupyter:
# Pkg.add("Plots") # 0.7.0 julia>] pkg>add Plots pkg>add GR pkg>add PyPlot pkg>add Gadfly pkg>add PlotlyJS pkg>add UnicodePlots
ليس من الضروري تثبيت جميع الحزم ، ولكن يجب أن تعرف أن كل منها له خصائصه الخاصة. أفضل plotlyjs () : على الرغم من أنها لا تختلف في السرعة ، إلا أنها تفاعلية للغاية. هناك تقريب ، يتحرك على طول الطائرة ، بالإضافة إلى القدرة على حفظ الملف ، وإذا قمت بحفظ مستند Jupyter بتنسيق html ، فسيتم حفظ جميع الميزات. لذا يمكنك الإضافة إلى الموقع أو تقديم عرض تفاعلي. مزيد من المعلومات على الصفحات: المؤامرات ، Gadfly
نمط رئيس لا نهاية لها
نفذت فكرة مقال عن هبر . بكلمات قليلة: ماذا لو أخذنا إحداثيات النقطة واستخدمنا عملية ، على سبيل المثال ، XOR أو أحادي المعامل وبين الإحداثي والإحداثيات ، ثم تحقق من الرقم من أجل البساطة أو للانتماء إلى أرقام فيبوناتشي ، وإذا كانت الإجابة نعم ، فاملأ النقطة بلون واحد ، ومع سلبي في آخر؟ تحقق:
للعملية٪ using Plots plotlyjs() function eratosphen(n, lst) # ar = [i for i=1:n] ar[1] = 0 for i = 1:n if ar[i] != 0 push!(lst, ar[i]) for j = i:i:n ar[j] = 0 end end end end ertsfn = [] eratosphen(1000, ertsfn) # print(ertsfn) # print( size(ertsfn) ) # -> 168 N = 80 M = 80 W1 = [in( x % y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x % y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y is prime?") p2 = spy(W2, title = "x % y") plot(p1, p2, layout=(2),legend=false)
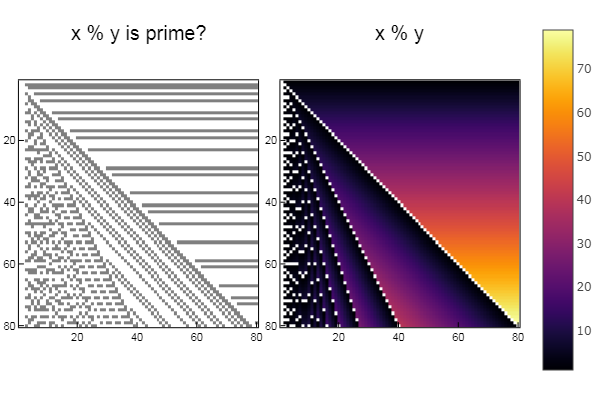
للعملية + W1 = [in( x + y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x + y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x + y is prime?") p2 = spy(W2, title = "x + y") plot(p1, p2, layout=(2),legend=false)
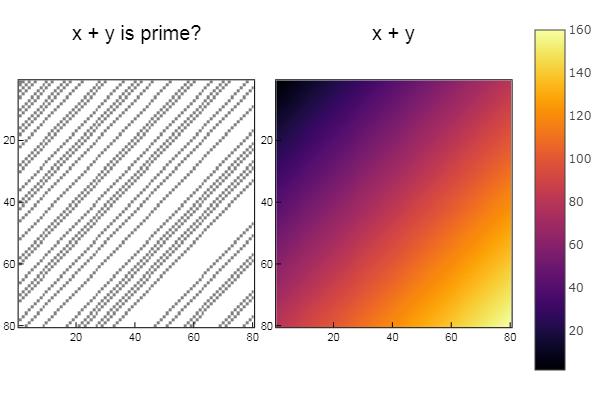
للتشغيل | W1 = [in( x | y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x | y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x | y is prime?") p2 = spy(W2, title = "x | y") plot(p1, p2, layout=(2),legend=false)

للتشغيل و W1 = [in( x & y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x & y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x & y is prime?") p2 = spy(W2, title = "x & y") plot(p1, p2, layout=(2),legend=false)
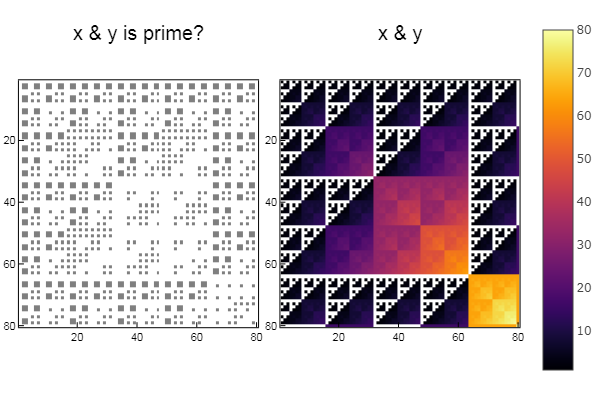
لعملية xor W1 = [in( xor(x, y), ertsfn) for x = 1:N, y = 1:M]; W2 = [xor(x, y) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y is prime?") p2 = spy(W2, title = "x xor y") plot(p1, p2, layout=(2),legend=false)
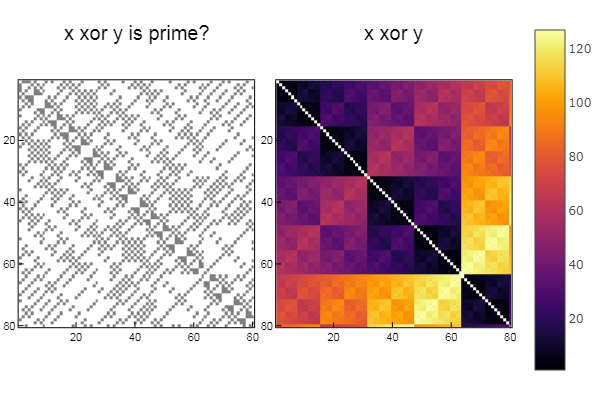
والآن كل شيء هو نفسه ، ولكن بالنسبة لأرقام فيبوناتشييمكنك عمل مسلسل كالمعتاد بشيء مثل:
function fib(n) a = 0 b = 1 for i = 1:n a, b = b, a + b end return a end fbncc = fib.( [i for i=1:10] )
ولكن دعونا نستخدم تمثيل المصفوفة ( بمزيد من التفاصيل ):
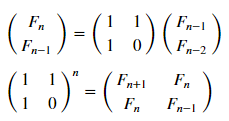
matr_fib = n -> [1 1; 1 0]^(n-1) # , n-1 mfbnc = [ matr_fib( i )[1,1] for i=1:17]; # 1,1 n- N = 100 M = N W1 = [in( x % y, mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x | y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y ∈ fibonacci?") p2 = spy(W2, title = "x | y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
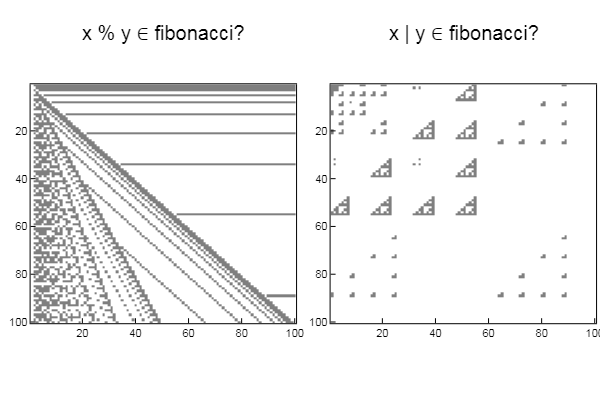
W1 = [in( xor(x, y), mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x & y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y ∈ fibonacci?") p2 = spy(W2, title = "x & y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
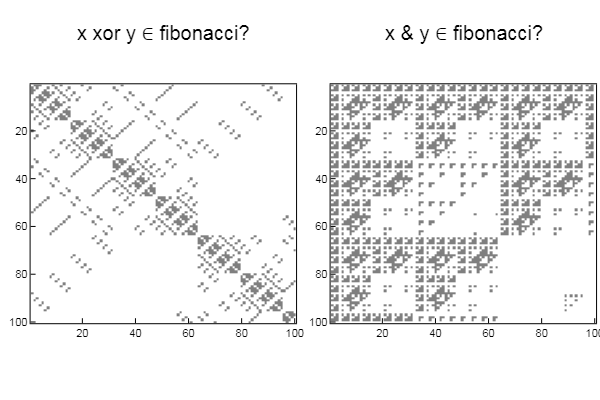
انعكاس شكل مستقيم نسبيًا
يتم تحديد هذا النوع من العرض من خلال المصفوفة:
[T]=[T′][R][R′][R]−1[T′]−1
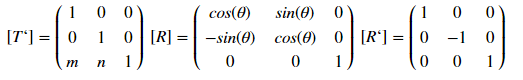
حيث [T '] و [R] و [R'] ، على التوالي ، مصفوفات الإزاحة والتدوير والانعكاس. كيف يعمل؟ دعنا نحلل مثالًا للإزاحة - بالنسبة للنقطة ذات الإحداثيات (س ، ص) ، سيتم تحديد الإزاحة بواسطة م × س و ن بواسطة اللعبة من خلال التحويل:
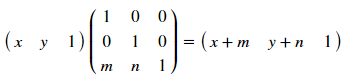
تسمح هذه المصفوفات بالتحويلات للمضلعات المختلفة ، والشيء الرئيسي هو تسجيل الإحداثيات تحت بعضها البعض وعدم نسيان عمود الوحدة في النهاية. وبالتالي [T]:
- يغير الخط عند الأصل مع المضلع الذي يتم تحويله
- قم بتدويره ليتزامن مع المحور X
- يعكس جميع نقاط المضلع فيما يتعلق بـ X
- متبوعًا بالدوران العكسي والنقل
يتم وصف الموضوع بمزيد من التفصيل في كتاب روجرز د. آدمز ج. الأسس الرياضية لرسومات الكمبيوتر
الآن كودها!
using Plots plotlyjs() f = x -> 0.4x + 2 # # X = [2 4 2 2]' Y = [4 6 6 4]' xs = [-2; 7] # ys = f(xs) inptmtrx = [ XY ones( size(X, 1), 1 ) ] # m = 0 n = -f(0) # Y displacement = [1 0 0; 0 1 0; mn 1] a = (ys[2]-ys[1]) / (xs[2]-xs[1]) # θ = -atan(a) rotation = [cos(θ) sin(θ) 0; -sin(θ) cos(θ) 0; 0 0 1] reflection = [1 0 0; 0 -1 0; 0 0 1] T = displacement * rotation * reflection * rotation^(-1) * displacement^(-1) # outptmtrx = inptmtrx * T plot( X, Y) plot!( xs, ys ) plot!( outptmtrx[:,1], outptmtrx[:,2] )
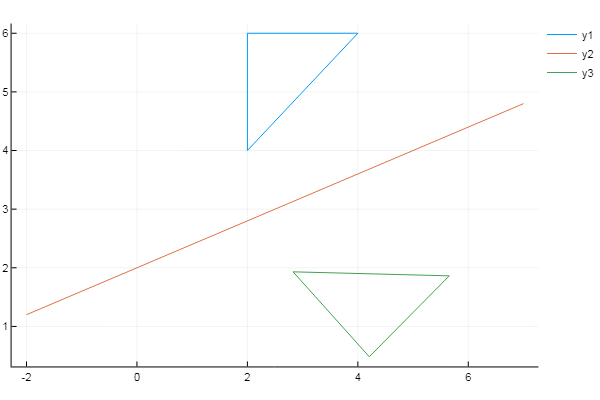
حقيقة مثيرة للاهتمام: إذا تخلصت من الأحرف اليونانية واستبدلت السطر الأول بـ
function y=f(x,t) y=0.4*x + 2 endfunction,
نظرًا لأن الأقواس [] تُؤطر فهارس المصفوفات على () ، والطوافات على plot( X, Y, xs, ys, trianglenew(:,1), trianglenew(:,2) ) ، فإن هذا الرمز يعمل إلى حد كبير في Scilab .
العمل مع رسومات ثلاثية الأبعاد
تدعم بعض هذه الحزم إنشاء رسوم بيانية ثلاثية الأبعاد. لكن أود أن أذكر بشكل منفصل أداة تصور قوية إلى حد ما ، والتي تعمل جنبًا إلى جنب مع حزم GLFW و GLAbraction التي تنفذ ميزات OpenGL في جوليا. مزيد من المعلومات حول Makie . نخفي استحسانه تحت
المفسد using Makie N = 51 x = linspace(-2, 2, N) y = x z = (-x .* exp.(-x .^ 2 .- (y') .^ 2)) .* 4 scene = wireframe(x, y, z) xm, ym, zm = minimum(scene.limits[]) scene = surface!(scene, x, y, z) contour!(scene, x, y, z, levels = 15, linewidth = 2, transformation = (:xy, zm)) scene
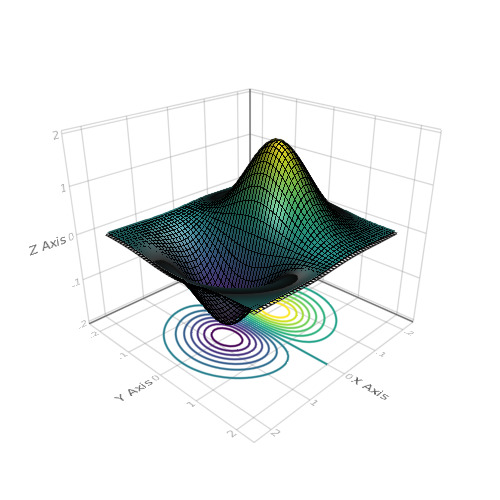
wireframe(Makie.loadasset("cat.obj"))

using FileIO scene = Scene(resolution = (500, 500)) catmesh = FileIO.load(Makie.assetpath("cat.obj"), GLNormalUVMesh) mesh(catmesh, color = Makie.loadasset("diffusemap.tga"))

x = Makie.loadasset("cat.obj") mesh(x, color = :black) pos = map(x.vertices, x.normals) do p, n p => p .+ (normalize(n) .* 0.05f0) end linesegments!(pos, color = :blue)
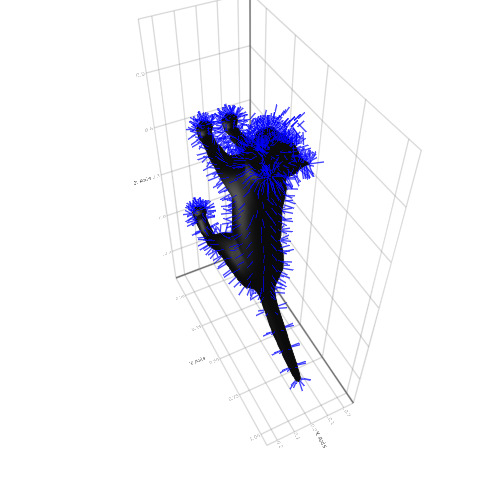
هذا كل شيء مع الرسومات. تفاعل ، رسوم متحركة ، بيانات ثلاثية الأبعاد ، بيانات كبيرة أو بناء سريع للرسوم البيانية البسيطة - ستلبي الحزم المتطورة باستمرار أي ذوق واحتياجات تقريبًا ، بالإضافة إلى أن كل شيء سهل التعلم. لا تتردد في تنزيل التمارين العملية والاستمرار في فهم جوليا!
تحديث: جميع القوائم المذكورة أعلاه مصنوعة في جوبيتر مع جوليا 0.6.4. لسوء الحظ ، تمت إزالة أو إعادة تسمية بعض وظائف الحزمة التعريفية لـ Plots ، لذلك نواصل المراقبة للحصول على التحديثات ، ولكن في الوقت الحالي يتم استبدال التجسس بالكامل:
julia> using GR julia> Z = [x | y for x = 1:40, y = 1:40]; julia> heatmap(Z)