
"الضبابية" في عامة الناس هو تأثير طمس في معالجة الصور الرقمية. يمكن أن يكون فعالًا جدًا في حد ذاته ومكونًا للرسوم المتحركة للواجهة ، أو تأثيرات مشتقة أكثر تعقيدًا (bloom / focusBlur / motionBlur). مع كل هذا ، الكآبة الصادقة في الجبين بطيئة نوعًا ما. وغالبًا ما تترك التطبيقات المضمنة في النظام الأساسي المستهدف الكثير مما هو مرغوب فيه. سواء كانت السرعة حزينة ، فإن القطع الأثرية تؤذي العينين. يؤدي الوضع إلى العديد من عمليات التسوية الأفضل أو الأسوأ المناسبة لظروف معينة. تنفيذ أصلي بجودة عالية من الموثوقية وأعلى سرعة ، بينما أقل اعتماد على الأجهزة في انتظارك تحت القطع. شهية طيبة!
(لابلاس بلور - اسم الخوارزمية الأصلي المقترح)
اليوم ، ركلني ديموغرافي الداخلي وأجبرني على كتابة مقال كان يجب كتابته قبل ستة أشهر. بصفتي أحد الهواة ، في أوقات الفراغ ، لتطوير خوارزميات التأثيرات الأصلية ، أود أن أقدم للجمهور خوارزمية "شبه غوسية زرقاء" ، تتميز باستخدام تعليمات المعالج بسرعة استثنائية (التحولات والأقنعة) ، وبالتالي يمكن الوصول إليها للتنفيذ حتى وحدات التحكم الدقيقة (سريعة للغاية في بيئة محدودة).
وفقًا لتقليدي في كتابة المقالات عن هبر ، سأقدم أمثلة في JS باعتبارها اللغة الأكثر شعبية ، وصدق أو لا تصدق ، إنها مناسبة جدًا لغرض إنشاء نماذج أولية سريعة للخوارزميات. بالإضافة إلى ذلك ، تأتي القدرة على تنفيذ ذلك بشكل فعال على JS مع صفائف مكتوبة. على جهاز الكمبيوتر المحمول غير القوي للغاية ، تتم معالجة صورة ملء الشاشة بسرعة 30 إطارًا في الثانية (لم يكن هناك تدخل متعدد للعمال).
إخلاء المسؤولية عن الرياضيات الرائعةسأقول على الفور إنني أخلع قبعتي لأنني أعتبر نفسي لست بارعًا بما فيه الكفاية في الرياضيات الأساسية. ومع ذلك ، فإنني أرشد دائمًا الروح العامة للنهج الأساسي. لذلك ، قبل أن تغش في نهجي "الملاحظة" إلى حد ما للتقريب ، احرص على حساب تعقيد البت للخوارزمية ، والذي ، كما تعتقد ، يمكن الحصول عليه من خلال طرق التقريب الكلاسيكية متعددة الحدود. خمنت صحيح؟ كنت تريد تقريبهم بسرعة؟ بالنظر إلى أنها تتطلب حسابًا عائمًا ، فستكون أبطأ بشكل كبير من نوبة بت واحدة ، والتي سأشرحها في النهاية. في كلمة واحدة ، لا تتسرع في الأصولية النظرية ، ولا تنس السياق الذي أحل فيه المشكلة.
هذا الوصف موجود هنا بدلاً من ذلك لشرح مسار أفكاري وتخميناتي التي قادتني إلى النتيجة. لمن يهمه الأمر:
وظيفة الغاوس الأصلي:
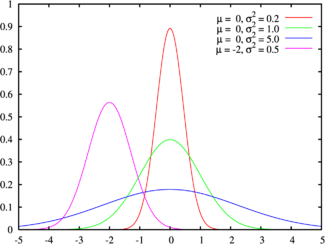
g (x) = a * e ** (- ((xb) ** 2) / c) ، حيث
a هي السعة (إذا كان لدينا ثمانية بتات من اللون لكل قناة ، فستكون = 256)
e هو ثابت أويلر ~ 2.7
ب - تحول الرسم البياني في س (لسنا بحاجة = 0)
ج - معلمة تؤثر على عرض الرسم البياني المرتبط بها كـ ~ w / 2.35
دالتنا الخاصة (ناقص من الأس الذي تمت إزالته باستبدال الضرب بالقسمة):
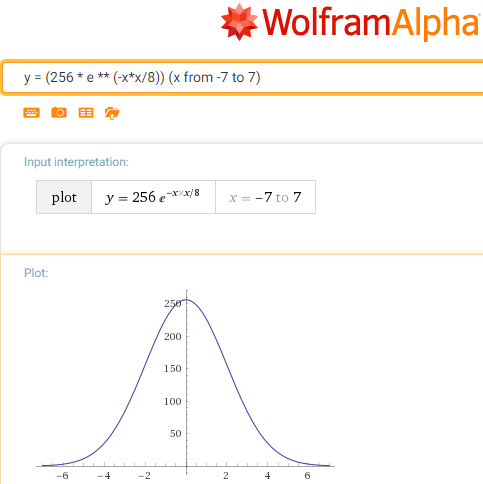
ز (خ) = 256 / ه ** (س * س / ج)
دع الإجراء التقريبي القذر يبدأ:
لاحظ أن المعلمة c قريبة جدًا من نصف العرض وتعيين 8 (هذا بسبب عدد الخطوات التي يمكنك تحويل قناة واحدة من 8 بت لكل منها).
نستبدل تقريبًا e بـ 2 ، مع ذلك ، مع ملاحظة أن هذا يؤثر على انحناء "الجرس" أكثر من حدوده. في الواقع ، يؤثر على 2 / e مرات ، ولكن المفاجأة هي أن هذا الخطأ يعوض عن المعلمة c ، بحيث لا تزال شروط الحدود منظمة ، ولا يظهر الخطأ إلا في "توزيع عادي" غير صحيح قليلاً ، للرسم الخوارزميات ، سيؤثر هذا على ديناميكيات التحولات اللونية المتدرجة ، ولكن يكاد يكون من المستحيل ملاحظة العين.
حتى الآن وظيفتنا هي كما يلي:
gg (x) = 256/2 ** (x * x / 8) أو gg (x) = 2 ** (8 - x * x / 8)
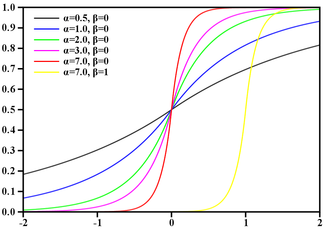
لاحظ أن الأس (x * x / 8) له نفس نطاق القيمة [0-8] مثل وظيفة القيمة المطلقة (x) ذات الترتيب الأدنى ، وبالتالي فإن الأخير هو مرشح للاستبدال. سوف نتحقق بسرعة من التخمين من خلال النظر في كيفية تغير الرسم البياني به gg (x) = 256 / (2 ** abs (x)):
GaussBlur vs LaplasBlur:
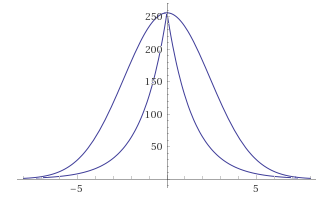
يبدو أن الانحرافات كبيرة جدًا ، علاوة على ذلك ، فإن الوظيفة ، بعد أن فقدت نعومتها ، لديها الآن ذروة. لكن مهلا.
أولاً ، دعونا لا ننسى أن نعومة التدرجات التي تم الحصول عليها عن طريق التمويه لا تعتمد على دالة كثافة الاحتمالية (وهي دالة Gaussian) ، ولكن على تكاملها - دالة التوزيع. في ذلك الوقت ، لم أكن أعرف هذه الحقيقة ، ولكن في الواقع ، بعد أن قمت بالتقريب "المدمر" فيما يتعلق بدالة كثافة الاحتمال (Gauss) ، ظلت وظيفة التوزيع متشابهة تمامًا.
كان:
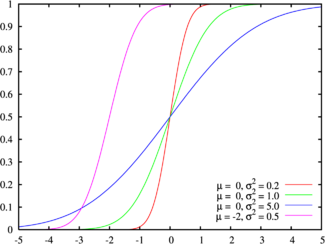
أصبح:
الدليل ، المأخوذ من الخوارزمية الجاهزة ، يتزامن:
(بالنظر إلى المستقبل ، سأقول أن الخطأ الضبابي في خوارزمي بالنسبة إلى Gausian x5 كان 3٪ فقط).
لذا ، فقد اقتربنا كثيرًا من دالة توزيع لابلاس. من كان يظن ، ولكن يمكنهم غسل الصور 97 ٪ ليس أسوأ.
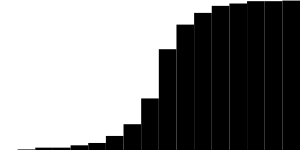
الدليل ، الاختلافات Gausian blura x5 و "Laplace blura" x7:

(هذه ليست صورة سوداء! يمكنك الدراسة في المحرر)
سمح لنا افتراض هذا التحول بالانتقال إلى فكرة الحصول على القيمة عن طريق التصفية التكرارية ، التي خططت للحد منها في البداية.
قبل إخبار خوارزمية معينة ، سيكون من الصادق إذا تقدمت للأمام وأصف على الفور عيبها الوحيد (على الرغم من أنه يمكن إصلاح التطبيق مع فقدان السرعة). ولكن يتم تنفيذ هذه الخوارزمية باستخدام الحساب القص ، وقوى 2 هي حدودها. لذلك تم عمل الأصل لطمس x7 (وهو الأقرب في الاختبارات لارتباط بـ Gausian x5). يرتبط هذا الحد من التنفيذ بحقيقة أنه مع لون ثمانية بت ، وتحويل القيمة في محرك التصفية بمقدار بت واحد لكل خطوة ، ينتهي أي تأثير من النقطة في 8 خطوات كحد أقصى. طبقت أيضًا إصدارًا أبطأ قليلاً من خلال النسب والإضافات الإضافية ، والتي تنفذ تقسيمًا سريعًا بمقدار 1.5 (مما ينتج عنه نصف قطر x15). ولكن مع التطبيق الإضافي لهذا النهج ، يزداد الخطأ ، وتنخفض السرعة ، مما لا يسمح باستخدامه بهذه الطريقة. من ناحية أخرى ، تجدر الإشارة إلى أن x15 يكفي لعدم ملاحظة الفرق كثيرًا ، ويتم الحصول على النتيجة من الأصل أو من الصورة التي تم أخذ عينات منها. لذا فإن الطريقة مناسبة تمامًا إذا كنت بحاجة إلى سرعة غير عادية في بيئة محدودة.
لذا ، فإن جوهر الخوارزمية بسيط ، يتم تنفيذ أربعة تمريرات من نفس النوع:
1. يضاف نصف قيمة محرك الأقراص t (مساويًا في البداية إلى صفر) إلى نصف قيمة البكسل التالي ، ويتم تعيين النتيجة له. استمر بهذه الطريقة حتى نهاية خط الصورة. لجميع الخطوط.
عند الانتهاء من التمرير الأول ، يتم تعتيم الصورة في اتجاه واحد.
2. بالممر الثاني نفعل نفس الشيء في الاتجاه المعاكس لجميع الخطوط.
نحصل على صورة مشوشة بشكل أفقي تمامًا.
3-4. الآن تفعل نفس الشيء عموديا.
انتهى!
في البداية ، استخدمت خوارزمية ثنائية التمرير مع تنفيذ التمويه الخلفي من خلال المكدس ، ولكن من الصعب فهمها ، وليس رشيقًا ، وتبين أنها أبطأ في البنى الحالية. ربما تكون خوارزمية التمرير الواحد أسرع في وحدات التحكم الدقيقة ، بالإضافة إلى القدرة على إخراج النتيجة بشكل تدريجي ستكون أيضًا ميزة إضافية.
طريقة التنفيذ الحالية الرباعية ، نظرت إلى حبري من المعلم السابق على خوارزميات التمويه.
habr.com/post/151157 انتهز هذه الفرصة لأعرب عن تضامني وامتناني العميق له.
لكن الاختراقات لم تنته عند هذا الحد. الآن حول كيفية حساب جميع قنوات الألوان الثلاثة في تعليمات معالج واحد! والحقيقة هي أن إزاحة البت المستخدمة كقسمة على اثنين تسمح لك بالتحكم بشكل جيد في موضع بتات النتيجة. المشكلة الوحيدة هي أن الأجزاء الصغيرة من القنوات تنزلق إلى القنوات المجاورة المجاورة ، ولكن يمكنك ببساطة إعادة تعيينها ، بدلاً من إصلاح المشكلة ، مع بعض فقدان الدقة. ووفقًا لصيغة المرشح الموصوفة ، فإن إضافة نصف قيمة محرك الأقراص مع نصف قيمة الخلية التالية (تخضع لإعادة تعيين البتات المفرغة) لا تؤدي أبدًا إلى تجاوز السعة ، لذلك لا داعي للقلق بشأن ذلك. وصيغة المرشح للحساب المتزامن لجميع الأرقام تصبح كما يلي:
buf32 [i] = t = (((t >> 1) & 0x7F7F7F) + ((buf32 [i] >> 1) & 0x7F7F7F) ؛
ومع ذلك ، هناك حاجة إلى إضافة واحدة أخرى: فقد تم العثور عليها تجريبيًا أن فقدان الدقة في هذه الصيغة مهم للغاية ، ويزداد سطوع الصورة بشكل ملحوظ. أصبح من الواضح أن الجزء المفقود يحتاج إلى تقريبه إلى أقرب كل ، وليس التخلص منه. طريقة سهلة للقيام بذلك في الحساب الصحيح هو إضافة نصف المقسوم قبل القسمة. المقسوم لدينا هو اثنان ، لذا تحتاج إلى إضافة واحد ، بكل الأرقام ، - الثابت 0x010101. ولكن مع أي إضافة ، يجب على المرء أن يكون حذرا من الحصول على تجاوز. لذلك لا يمكننا استخدام مثل هذا التصحيح لحساب نصف قيمة الخلية التالية. (إذا كان هناك لون أبيض ، فسنحصل على الفائض ، وبالتالي لن نقوم بتصحيحه). ولكن اتضح أن الخطأ الرئيسي تم عن طريق تقسيم متعدد لمحرك الأقراص ، والذي يمكننا تصحيحه فقط. لأنه في الواقع ، حتى مع هذا التصحيح ، لن ترتفع القيمة في محرك الأقراص فوق 254. ولكن عند إضافته إلى 0x010101 ، لن يتم ضمان الفائض. وتأخذ صيغة المرشح مع التصحيح الشكل التالي:
buf32 [i] = t = ((((((0x010101 + t) >> 1) & 0x7F7F7F) + ((buf32 [i] >> 1) & 0x7F7F7F) ؛
في الواقع ، تقوم الصيغة بإجراء التصحيح بشكل جيد ، لذلك عندما تقوم بتطبيق هذه الخوارزمية بشكل متكرر على الصورة ، تبدأ القطع في الظهور فقط في الممرات العشرة الثانية. (ليس حقيقة أن تكرار غوسان بلورا لن ينتج مثل هذه القطع الأثرية).
بالإضافة إلى ذلك ، هناك خاصية رائعة مع العديد من التصاريح. (هذا ليس بسبب خوارزمي ، ولكن بسبب "طبيعية" التوزيع الطبيعي). بالفعل في الممر الثاني من لابلاس بلورا ، ستبدو دالة كثافة الاحتمال (إذا اكتشفت كل شيء بشكل صحيح) شيئًا مثل هذا:
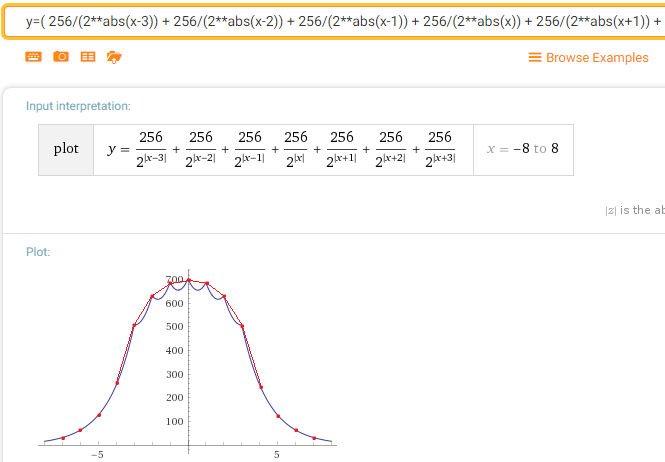
وهو ، كما ترى ، قريبًا جدًا من الغاوسي.
تجريبيا ، وجدت أن استخدام التعديلات ذات نصف قطر كبير مسموح به في أزواج ، لأنه تعوض الخاصية الموضحة أعلاه عن الأخطاء إذا كان التمرير الأخير أكثر دقة (الأكثر دقة هو خوارزمية طمس x7 الموضحة هنا).
تجريبيرابالشفرةنداء لرياضيين باردين:
من المثير للاهتمام معرفة مدى صحة استخدام مثل هذا الفلتر بشكل منفصل ، لست متأكدًا مما إذا كانت هناك صورة توزيع متماثلة. على الرغم من أن عدم تجانس العين غير مرئي.
محدث: هنا سوف أقوم برفع روابط مفيدة ، يرجى تقديمها من قبل المعلقين ، والتي تم العثور عليها من الخبروفيين الآخرين.
1. كيفية عمل معالجات Intel استنادًا إلى قوة SSE -
software.intel.com/en-us/articles/iir-gaussian-blur-filter-implementation-using-intel-advanced-vector-extensions (شكرًا
vladimirovich )
2. قاعدة نظرية حول موضوع "ملتقيات الصور السريعة" + بعض تطبيقاتها المخصصة فيما يتعلق
بصدق غاوسي
بلوير -
blog.ivank.net/fastest-gaussian-blur.html (شكرا
Grox )
نرحب بالاقتراحات والتعليقات والنقد البناء!