التحقق العددي من فرضية ABC (نعم ، هذا واحد)

مرحباً هابر.

كانت هناك بالفعل العديد من المقالات حول فرضية ABC في Geektimes Habr (على سبيل المثال ، في 2013 و 2018 ). القصة نفسها عن نظرية لا يمكن إثباتها في البداية لسنوات عديدة ، ثم لا يمكن التحقق منها لنفس عدد السنوات ، تستحق بالتأكيد فيلمًا روائيًا على الأقل. ولكن في ظل هذه القصة الرائعة ، تعتبر النظرية نفسها سطحية للغاية ، على الرغم من أنها ليست أقل إثارة للاهتمام. بالفعل على الأقل من خلال حقيقة أن فرضية ABC هي واحدة من المشكلات القليلة التي لم يتم حلها في العلوم الحديثة ، وبيان المشكلة الذي يمكن حتى الصف الخامس فهمه. إذا كانت هذه الفرضية صحيحة حقًا ، فعندئذٍ يمكن أن تتبع بسهولة من إثبات نظريات مهمة أخرى ، على سبيل المثال ، إثبات نظرية فيرمات .

دون أن أدعي أمراء موتيزوكي ، قررت أيضًا أن أحاول وقررت أن أتحقق مع جهاز الكمبيوتر من مدى تحقيق المساواة الموعودة في الفرضية. في الواقع ، لماذا لا - المعالجات الحديثة ليست فقط للعب الألعاب - لماذا لا تستخدم جهاز كمبيوتر لغرضه الرئيسي (الحوسبة) ...

من يهتم بما حدث ، من فضلك ، تحت القطة.

بيان المشكلة

لنبدأ من البداية. ما هي النظرية؟ كما تقول ويكيبيديا (الصياغة في النسخة الإنجليزية أكثر وضوحًا قليلاً) ، للأرقام البسيطة المتبادلة (التي لا تحتوي على قواسم مشتركة) أ ، ب و ج بحيث أن أ + ب = ج ، لأي ε> 0 هناك عدد محدود من ثلاث مرات أ + ب = c ، بحيث:



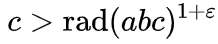
تسمى دالة rad الراديكالية ، وتشير إلى نتاج العوامل الأولية لرقم. على سبيل المثال ، rad (16) = rad (2 * 2 * 2 * 2) = 2 ، rad (17) = 17 (17 هو رئيس) ، rad (18) = rad (2 * 3 * 3) = 2 * 3 = 6 ، راد (1،000،000) = راد (2 ^ 6 ⋅ 5 ^ 6) = 2 * 5 = 10.

في الواقع ، جوهر النظرية هو أن عدد هذه الثلاثيات صغير جدًا. على سبيل المثال ، إذا أخذنا عشوائيًا ε = 0.2 والمساواة 100 + 27 = 127: rad (100) = rad (2 * 2 * 5 * 5) = 10 ، rad (27) = rad (3 * 3 * 3) = 3 ، rad (127) = 127، rad (a * b * c) = rad (a) * rad (b) * rad (c) = 3810، 3810 ^ 1.2 أكبر بشكل واضح من 127 ، عدم المساواة لا تصمد. ولكن هناك استثناءات ، على سبيل المثال ، للمساواة 49 + 576 = 625 ، يتم تحقيق شرط النظرية (أولئك الذين يرغبون في التحقق من تلقاء أنفسهم).

اللحظة الرئيسية التالية بالنسبة لنا هي عدد محدود من هذه المساواة ، وفقًا للنظرية. على سبيل المثال هذا يعني أنه يمكنك ببساطة محاولة فرزها جميعًا على جهاز كمبيوتر. ونتيجة لذلك ، يعطينا هذا جائزة نوبل مهمة برمجة مثيرة للاهتمام.

لذلك دعونا نبدأ.

كود المصدر

تمت كتابة النسخة الأولى بلغة Python ، وعلى الرغم من أن هذه اللغة بطيئة جدًا في مثل هذه الحسابات ، إلا أن كتابة التعليمات البرمجية عليها سهلة وبسيطة ، وهي ملائمة للنماذج الأولية.

الحصول على الجذر : نحن نحلل الرقم إلى عوامل أولية ، ثم نزيل التكرارات ، ونحول الصفيف إلى مجموعة. ثم مجرد الحصول على منتج لجميع العناصر.

def prime_factors(n): factors = [] # Print the number of two's that divide n while n % 2 == 0: factors.append(int(2)) n = n / 2 # n must be odd at this point so a skip of 2 ( i = i + 2) can be used for i in range(3, int(math.sqrt(n)) + 1, 2): # while i divides n , print i ad divide n while n % i == 0: factors.append(int(i)) n = n / i # Condition if n is a prime number greater than 2 if n > 2: factors.append(int(n)) return set(factors) def rad(n): result = 1 for num in prime_factors(n): result *= num return result 

الأعداد الأولية المتبادلة : احسب الأرقام ، وتحقق فقط من تقاطع المجموعات.

 def not_mutual_primes(a,b,c): fa, fb, fc = prime_factors(a), prime_factors(b), prime_factors(c) return len(fa.intersection(fb)) == 0 and len(fa.intersection(fc)) == 0 and len(fb.intersection(fc)) == 0 

تحقق : نستخدم وظائف تم إنشاؤها بالفعل ، كل شيء بسيط هنا.

 def check(a,b,c): S = 1.2 # Eps=0.2 if c > (rad(a)*rad(b)*rad(c))**S and not_mutual_primes(a, b, c): print("{} + {} = {} - PASSED".format(a, b, c)) else: print("{} + {} = {} - FAILED".format(a, b, c)) check(10, 17, 27) check(49, 576, 625) 

يمكن لأولئك الذين يرغبون في التجربة بشكل مستقل عن طريق نسخ الرمز أعلاه إلى أي محرر لغة Python عبر الإنترنت. بالطبع ، يعمل الكود كما هو متوقع كما هو متوقع ، وسيكون تعداد جميع الثلاثيات إلى مليون على الأقل طويلًا جدًا. تحت المفسد هناك نسخة محسنة ، فمن المستحسن استخدامه.

تمت إعادة كتابة النسخة النهائية في C ++ باستخدام تعدد مؤشرات الترابط وبعض التحسين (العمل في C مع مجموعات متقاطعة سيكون شديد الصعوبة ، على الرغم من أنه ربما أسرع). كود المصدر تحت المفسد ، يمكن تجميعه في مترجم g ++ المجاني ، يعمل الرمز تحت Windows و OSX وحتى على Raspberry Pi.


بالنسبة لأولئك الذين هم كسالى للغاية لتثبيت مترجم C ++ ، يتم توفير إصدار Python محسن قليلاً ، والذي يمكن إطلاقه في أي محرر عبر الإنترنت (استخدمت https://repl.it/languages/python ).

النتائج

الثلاث مرات ، أ ، ب ، ج قليلة جدًا حقًا.

يتم إعطاء بعض النتائج أدناه:
N = 10 : 1 "ثلاثة" ، مهلة <0.001c
1 + 8 = 9

N = 100 : 2 "ثلاث مرات" ، وقت التشغيل <0.001c
1 + 8 = 9
1 + 80 = 81

N = 1000 : 8 "ثلاث مرات" ، وقت التشغيل <0.01c
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
3 + 125 = 128
13 + 243 = 256
49 + 576 = 625

N = 10000 : 23 "ثلاث مرات" ، وقت التشغيل 2 ثانية


N = 100000 : 53 ثلاث مرات ، وقت التشغيل 50 ج


مع N = 1،000،000 ، لدينا 102 "ثلاث مرات" فقط ، يتم إعطاء قائمة كاملة تحت المفسد.


للأسف ، لا يزال البرنامج يعمل ببطء ، ولم أنتظر نتائج N = 10000000 ، ووقت الحساب أكثر من ساعة (ربما أخطأت في تحسين الخوارزمية في مكان ما ، ويمكنني القيام بعمل أفضل).

والأكثر إثارة للاهتمام هو النظر إلى النتائج بيانياً:



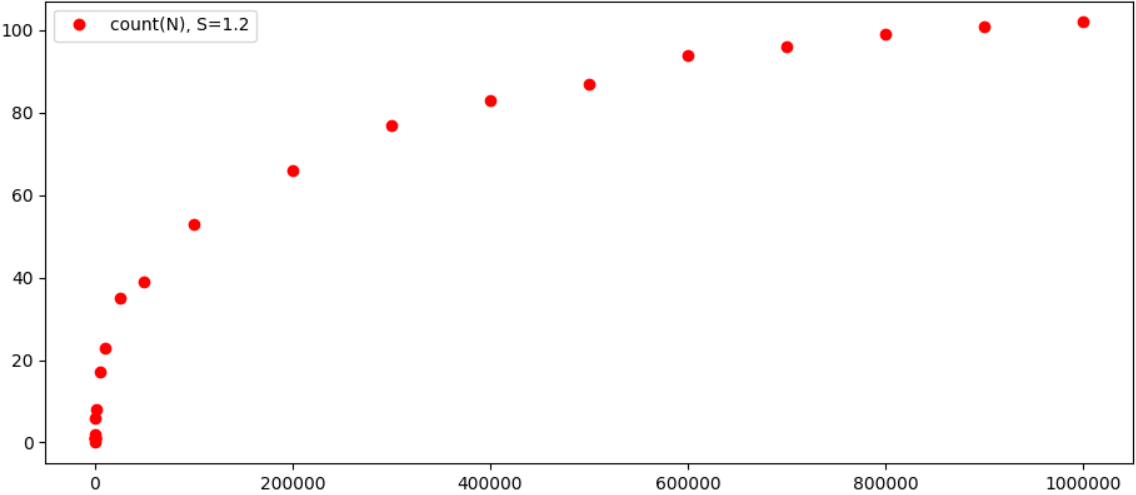
من حيث المبدأ ، من الواضح تمامًا أن اعتماد عدد الثلاثيات المحتملة على N ينمو بشكل أبطأ بشكل ملحوظ من N نفسه ، ومن المحتمل أن تتقارب النتيجة إلى عدد معين لكل ε. بالمناسبة ، مع زيادة ε ، ينخفض ​​عدد "الثلاثيات" بشكل ملحوظ ، على سبيل المثال ، بالنسبة لـ ε = 0.4 ، لدينا فقط متساوين لـ N <100000 (1 + 4374 = 4375 و 343 + 59049 = 59392). لذلك بشكل عام ، يبدو أن النظرية صحيحة حقًا (حسنًا ، وربما تم اختبارها بالفعل على أجهزة كمبيوتر أكثر قوة ، وربما تم حساب كل هذا منذ فترة طويلة).

يمكن لأولئك الذين يرغبون في التجربة بمفردهم ، إذا كان أي شخص لديه نتائج للأرقام 10،000،000 وأعلى ، فسأكون سعيدًا بإضافتها إلى المقالة. بالطبع ، سيكون من المثير للاهتمام "العد" حتى اللحظة التي تتوقف فيها مجموعة "الثلاثيات" تمامًا عن النمو ، ولكن يمكن أن تستغرق وقتًا طويلاً حقًا ، ويبدو أن سرعة الحساب تعتمد على N كـ N * N (أو ربما N ^ 3) ، والعملية طويل جدا. ومع ذلك ، هناك شيء رائع قريب ، وقد يرغب أولئك الذين يرغبون في الانضمام إلى البحث.

تحرير: كما هو مقترح في التعليقات ، فإن ويكيبيديا لديها بالفعل جدول بالنتائج - في النطاق N حتى 10 ^ 18 لا يزال عدد "الثلاثيات" في ازدياد ، لذلك لم يتم العثور على "نهاية" المجموعة حتى الآن. الأكثر إثارة للاهتمام - دسيسة لا تزال قائمة.