في مارس 2016 ،
افتتح روبرت جيه. ليمكي - أوليفر وكانان سونداراراجان من جامعة ستانفورد
نمطًا جديدًا في توزيع الأعداد الأولية. اتضح أن الأعداد الأولية يتم توزيعها بشكل
خاص على مساحة الرقم. لمزيد من التفاصيل انظر ترجمة مقالة
"هيكلية وعشوائية الأعداد الأولية" على حبري.
انضم خبراء من مجالات أخرى ، بما في ذلك الكيمياء ، في دراسة الموضوع. وبنجاح. اكتشف أستاذ الكيمياء النظرية
سالفاتور توركواتو ، إلى جانب المنظر
ماثيو دي كورسي - أيرلندا ، أنماطًا جديدة في توزيع الأعداد الأولية التي لم تكن معروفة من قبل. اتضح أن توزيع الأعداد الأولية يشكل نمط حيود يشبه الفركتل ، يشبه إلى حد ما نمط الحيود من البلورات شبه الغريبة.
البروفيسور Torcuato متخصص في دراسة الأنماط في هياكل النظم الفيزيائية ، مثل البلورات والغرويات. الطريقة القياسية لدراسة الهيكل هي حيود الأشعة السينية. تعكس الجزيئات العشوائية في السوائل أو الغازات الأشعة في جميع الاتجاهات دون إنشاء نمط ملحوظ. لكن الذرات الموجودة بشكل متناظر في بلورة تعكس بشكل متزامن موجات الضوء ، مما يخلق بقع مشرقة دورية من الحيود الواضح (
قمم Bragg ). إن تحليل قمم Bragg يجعل من الممكن فهم البنية الداخلية للبلورة أو مادة أخرى تخلق مثل هذه الصورة.
لذلك ، في مقالات علمية جديدة كتبها Torkuato وآخرون (
1 ،
2 ،
3 ) ، تبين أن البنية المرتبة المكتشفة في توزيع الأعداد الأولية ليست سوى نمط حيود يشبه الفركتل ، مشابه لنمط البلورات شبه.
صورة قمم Bragg على شبكة من الأعداد الأولية تشبه البلورات شبه ، لكنها لا تزال تختلف عنها.
يقول Torcuato أن الأعداد الأولية كنظام مادي "هي فئة جديدة تمامًا من الهياكل". أطلق الباحثون على هذا النمط الجديد الذي يشبه الفراكتل "تواتر الحد الفعال".
يتكون الشكل من تسلسل دوري للقمم الساطعة التي تعكس أكثر فترات الرقم الأولي شيوعًا: كلها غريبة (باستثناء 2) ، والعديد منها بجانب بعضها البعض. تتألق قمم ألمع (أزواج مفصولة برقمين) على فترات منتظمة مع قمم أقل سطوعًا ، مما يعكس الأعداد الأولية مفصولة بستة أرقام. فيما بينها توجد قمم أكثر خفة تتوافق مع أزواج الأعداد الأولية البعيدة ، وما إلى ذلك. كل هذا عدد لا نهائي من قمم Bragg الموضوعة داخل بعضها البعض.
لوحظت بنية مماثلة لقمم Bragg في وقت سابق - في أنماط الحيود من البلورات شبه البلورية.
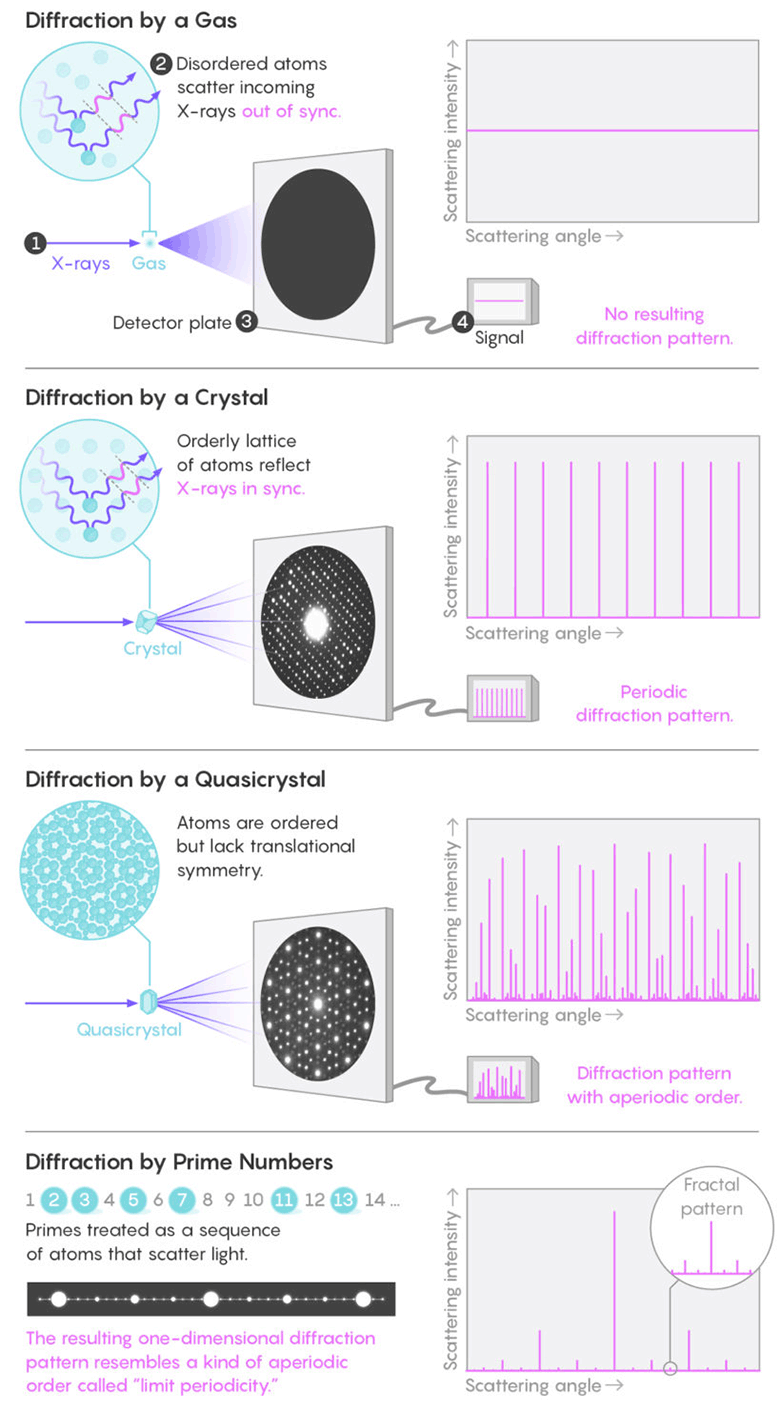تعكس الجزيئات العشوائية في السوائل أو الغازات الأشعة في جميع الاتجاهات دون إنشاء نمط ملحوظ. لكن الذرات الموجودة بشكل متناظر في بلورة تعكس بشكل متزامن موجات الضوء ، مما يخلق بقع مشرقة دورية من الحيود الواضح. كما اتضح ، فإن نمط توزيع الأعداد الأولية يشكل نمط حيود كسري ، مشابه لنمط البلورات شبهالبلورات شبه البلورية هي مواد غريبة تم اكتشافها في الثمانينيات. وتتميز بالتناظر المحظور في علم البلورات الكلاسيكي ووجود ترتيب بعيد المدى. تعتبر الفسيفساء غير الدورية من نوع
فسيفساء بنروز الشهيرة نموذجًا رياضيًا للبلورات شبه البلورية. في هذه الفسيفساء ، التماثل الانتقالي غائب ، وتكرار التكرار وشبه التبلور موجود (التماثل من الدرجة الخامسة).
جزء من فسيفساء بنروز من النوع P1 (من البلاط من ستة أنواع)في حالة الأعداد الأولية ، تتناسب المسافات بين القمم مع بعضها البعض ، على النقيض من قمم Bragg متباعدة بشكل غير منطقي من البلورات شبه.
قال Torcuato "الأعداد الأولية تعني في الواقع حالة مختلفة تمامًا من مواضع الجسيمات ، على غرار البلورات شبه البلورية ، ولكنها ليست مثل البلورات شبه البلورية".
لا يمكن أن يسمى اكتشاف نمط الحيود اكتشافًا مذهلاً لنظرية الأعداد ، لأن الجزء الرئيسي من هذه الأنماط قد تم وصفه سابقًا ، فقط من خلال الطرق الرياضية الأخرى (ليس من خلال حيود البلورات شبه). لذا ، باستخدام نمط الحيود ، من الممكن التنبؤ بـ "الزوجين" من النوعين 17 و 19 - وهذا هو المعادل الرياضي
لفرضية هاردي - ليتلوود الأولى فيما يتعلق بوجود مجموعات من الأعداد الأولية في مقطع معين من خط الأعداد. تحظر إحدى القواعد ثلاثة توائم من الأرقام الفردية المتتالية بعد {3 ، 5 ، 7}. يفسر هذا أيضًا سبب توافق قمة ألمع Bragg التالية في نمط الحيود إلى أرقام مفصولة بستة أرقام بدلاً من أربعة.
إن العمل العلمي الجديد هو مجرد نظرة جديدة على مشكلة التوزيع الموحد للأعداد الأولية وطريقة أسهل لاشتقاق "قانون واحد" معين لهم. بالإضافة إلى ذلك ، فهذه طريقة غير عادية لتحليل مشكلة رياضية من وجهة نظر علم البلورات ، أي من وجهة نظر مجال بحث صغير نسبيًا يسمى "الترتيب غير الدوري" ، الذي يدرس النماذج غير المتكررة ويكمن في تقاطع علم البلورات والأنظمة الديناميكية والتحليل التوافقي والهندسة المنفصلة. نما هذا الفرع من العلوم بعد اكتشاف البلورات شبه البلورية ، عندما اتضح أن الأساليب القديمة لم تنجح هنا.
يشبه توزيع الأعداد الأولية نظامًا غير دوري خاصًا ، معروفًا منذ الخمسينيات. يطلق عليه دورية الحد. في مثل هذه الأنظمة ، تتداخل الفترات الدورية في تسلسل هرمي لا نهائي ، بحيث يحتوي النظام في أي فاصل زمني على أجزاء من الأنماط التي تتكرر فقط في فاصل زمني أكبر ، كما هو الحال في بلاط تايلور-سوكولار.
بلاط تايلور سوكولارتظهر الحسابات النظرية أن المراحل الدورية القصوى للمادة يجب أن تكون قادرة على التكوين في الطبيعة ، وقد يكون لهذه الأنظمة خصائص غير عادية. ولكن لم يخمن أحد ربط الفترة الزمنية المحددة بالأعداد الأولية. نحن نعلم الآن أن هناك مثل هذا الاتصال ، والأرقام الأولية تُظهر نوعًا جديدًا من دورية الحد - دورية حد "فعالة" ، لأن التزامن في المسافات بين الأعداد الأولية في جميع أنحاء النظام يتم ملاحظته إحصائيًا فقط.
السؤال الذي يطرح نفسه: كيف يمكن أن تؤثر أنماط توزيع الأعداد الأولية على قوة خوارزميات التشفير؟
"أحصل على العديد من الرسائل حول هذا الموضوع. على الرغم من أن هذه دراسة مثيرة للاهتمام ، إلا أنها لا علاقة لها بالتشفير "،
كتب عالم التشفير الشهير بروس شناير في مدونته. - لا يهتم المبرمجون بإيجاد الأعداد الأولية أو حتى توزيعها. يرتبط استمرار خوارزميات تشفير المفتاح العام من نوع RSA بصعوبة معالجة الأعداد المركبة الكبيرة ، والتي هي نتاج الأعداد الأولية. وهذه مسألة مختلفة تمامًا. "
لذلك على الرغم من التقدم المحرز في دراسة توزيع الأعداد الأولية ، فلا داعي للقلق بشأن قوة رموز التشفير حتى الآن.
