حول قابلية حل مشاكل الحزام في زمن كثير الحدود

يتعرف الطلاب على مشكلة الحزام عن طريق أخذ دورات المعلوماتية الحيوية ، على وجه الخصوص ، واحدة من أعلى مستويات الجودة وأوثق روح للمبرمجين هي دورة المعلوماتية الحيوية (Pavel Pevzner) في الدورات الدراسية من جامعة كاليفورنيا في سان دييغو. تجذب المشكلة الانتباه من خلال بساطة البيان ، والأهمية العملية ، وحقيقة أنه لا يزال يعتبر غير محلول مع القدرة الواضحة على حلها باستخدام الترميز البسيط. المشكلة تطرح بهذه الطريقة. هل من الممكن استعادة إحداثيات مجموعة من النقاط في وقت كثير الحدود$$ $ مضمنة $ X $ مضمنة $ إذا كانت مجموعة جميع المسافات بين الزوجين معروفة$$ $ inline $ \ Delta X $ inline $ ؟؟؟

لا تزال هذه المهمة التي تبدو بسيطة على قائمة المشكلات التي لم يتم حلها للهندسة الحسابية. علاوة على ذلك ، فإن الوضع لا يتعلق حتى بالنقاط في المساحات متعددة الأبعاد ، وخاصة المساحات المنحنية ، فإن المشكلة هي بالفعل أبسط خيار - عندما يكون لجميع النقاط إحداثيات صحيحة ويتم تحديد موقعها على نفس الخط.

في ما يقرب من نصف قرن منذ أن اعتبر علماء الرياضيات هذه المهمة بمثابة تحد (Shamos، 1975) ، تم الحصول على بعض النتائج. نعتبر حالتين ممكنتين لمشكلة أحادية البعد:

1. تقع النقاط على خط مستقيم (مشكلة دوران)
2. تقع النقاط على دائرة (مشكلة الحزام)

تلقت هاتان الحالتان أسماء مختلفة لسبب ما - يتطلب الأمر جهودًا مختلفة لحلها. في الواقع ، تم حل المهمة الأولى بسرعة كافية (في 15 عامًا) وتم بناء خوارزمية رجعية ، والتي تعيد الحل في المتوسط ​​في الوقت التربيعي$$ $ inline $ O (n ^ 2 \ log n) $ inline $ أين$$ $ مضمنة $ n $ مضمنة $ - عدد النقاط (Skiena، 1990) ؛ بالنسبة للمهمة الثانية ، لم يتم القيام بذلك حتى الآن ، ولأفضل خوارزمية مقترحة تعقيد حسابي أسي$$ $ inline $ O (n ^ n \ log n) $ inline $ (لمكه ، 2003). توضح الصورة أدناه تقديرًا للمدة التي سيعمل فيها جهاز الكمبيوتر الخاص بك للحصول على حل لمجموعة تحتوي على عدد مختلف من النقاط.



أي أنه في وقت مقبول نفسياً (~ 10 ثوانٍ) ، يمكنك استعادة الكثير$$ $ مضمنة $ X $ مضمنة $ ما يصل إلى 10 آلاف نقطة في حالة دوران و 10 نقاط فقط لحالة الحزام ، والتي لا قيمة لها على الإطلاق للتطبيقات العملية.

القليل من التوضيح. يُعتقد أن مشكلة Turnpike تم حلها من حيث الاستخدام العملي ، أي بالنسبة للغالبية العظمى من البيانات التي تمت مواجهتها. في هذه الحالة ، اعتراضات علماء الرياضيات البحتين على حقيقة أن هناك مجموعات بيانات خاصة يتم تجاهل وقت الحصول على حل لها بشكل أسي$$ $ inline $ O (2 ^ n \ log n) $ inline $ (Zhang ، 1982). على عكس Turnpike ، لا يمكن اعتبار مشكلة الحزام مع الخوارزمية الأسية محلولة بأي شكل من الأشكال.

أهمية حل مشاكل الحزام من ناحية المعلوماتية الحيوية

في نهاية القرن العشرين ، تم اكتشاف مسار جديد لتوليف الجزيئات الحيوية ، يسمى المسار غير الريبوسومي للتوليف. اختلافه الرئيسي عن مسار التوليف الكلاسيكي هو أن نتيجة التوليف النهائية ليست مشفرة في DNA على الإطلاق. بدلاً من ذلك ، يتم فقط كتابة رمز "الأدوات" (العديد من المواد التركيبية المختلفة) التي يمكنها جمع هذه الأشياء في DNA. وبالتالي ، يتم إثراء هندسة الآلات الحيوية بشكل كبير ، وبدلاً من نوع واحد من المجمعات (الريبوسوم) ، الذي يعمل مع 20 جزءًا قياسيًا فقط (الأحماض الأمينية القياسية ، وتسمى أيضًا بروتين المنشأ) ، تظهر العديد من الأنواع الأخرى من المجمعات التي يمكن أن تعمل مع أكثر من 500 جزء قياسي وغير قياسي (الأحماض الأمينية غير البروتينية وتعديلاتها المختلفة). ولا يمكن لهذه المجمعات فقط توصيل الأجزاء بالسلاسل ، ولكن أيضًا الحصول على هياكل معقدة للغاية - دورية ، متفرعة ، وكذلك هياكل ذات العديد من الدورات والفروع. كل هذا يزيد بشكل كبير من ترسانة الخلية في حالات مختلفة من حياتها. النشاط البيولوجي لهذه الهياكل مرتفع ، ونوعية (انتقائية العمل) ، أيضًا ، مجموعة متنوعة من الخصائص غير محدودة. تسمى فئة هذه المنتجات الخلوية في الأدب الإنجليزي NRPs (المنتجات غير الريبوسومية ، أو الببتيدات غير الريبوسومية). يأمل علماء الأحياء في أنه من بين منتجات التمثيل الغذائي للخلايا على وجه التحديد ، يمكن العثور على مستحضرات دوائية جديدة ذات فعالية عالية وليس لها آثار جانبية بسبب الخصوصية.

السؤال الوحيد هو كيف وأين تبحث عن NRPs؟ فهي فعالة للغاية ، وبالتالي لا تحتاج الخلية على الإطلاق إلى إنتاجها بكميات كبيرة ، وتركيزاتها ضئيلة. لذا فإن طرق الاستخلاص الكيميائي مع دقتها المنخفضة التي تبلغ ~ 1٪ والكاشف الضخم وتكاليف الوقت غير مجدية. التالي. لا يتم ترميزها في الحمض النووي ، مما يعني أن جميع قواعد البيانات التي تم تجميعها أثناء فك تشفير الجينوم ، وجميع طرق المعلوماتية الحيوية وعلم الجينوم ، هي أيضًا غير مجدية. الطريقة الوحيدة للعثور على شيء ما هي من خلال الطرق الفيزيائية ، أي التحليل الطيفي الكتلي. علاوة على ذلك ، فإن مستوى الكشف عن المواد في مقاييس الطيف الحديثة مرتفع للغاية لدرجة أنه يسمح للمرء بالعثور على كميات غير ذات أهمية ، في المجموع> ~ 800 جزيء (مدى أتو مولار ، أو التركيز$$ $ مضمنة $ 10 ^ {- 18} $ مضمنة $ )

"

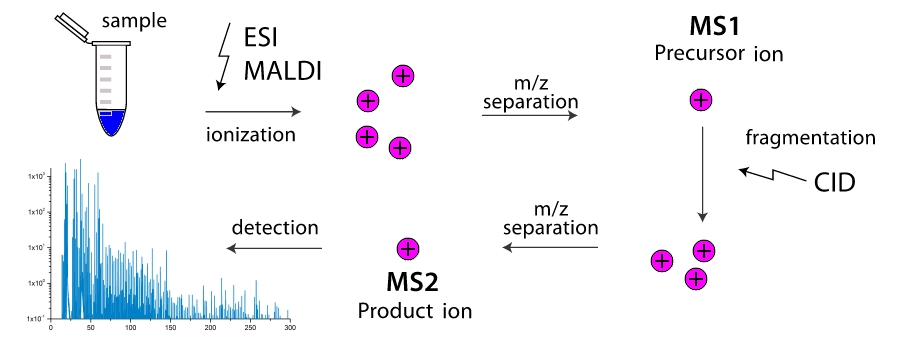
كيف يعمل مطياف الكتلة؟ في غرفة العمل بالجهاز ، يتم تقسيم الجزيئات إلى شظايا (في كثير من الأحيان من خلال اصطدامها مع بعضها البعض ، أقل بسبب التأثيرات الخارجية). تتأين هذه الأجزاء ، ثم يتم تسريعها وفصلها في مجال كهرومغناطيسي خارجي. يحدث الفصل إما عندما يصل الكاشف ، أو بزاوية المنعطف في المجال المغناطيسي ، لأن كتلة الشظية أكبر وشحنتها أقل ، كلما كانت أكثر خرقاء. وهكذا ، فإن مطياف الكتلة "يزن" كتل الشظايا. علاوة على ذلك ، يمكن إجراء "الوزن" على مراحل ، من خلال تصفية الأجزاء بشكل متكرر بالكتلة نفسها (بشكل أكثر دقة ، مع قيمة واحدة$$ $ مضمنة $ m / z $ مضمنة $ ) ودفعهم من خلال التجزؤ مع مزيد من الفصل. يتم توزيع مطياف الكتلة بمرحلتين على نطاق واسع ويطلق عليها مطياف الكتلة الترادفية ، وتكون مطياف الكتلة متعددة المراحل نادرة للغاية ، ويتم تصنيفها ببساطة على أنها$$ $ inline $ ms ^ n $ مضمنة $ أين$$ $ مضمنة $ n $ مضمنة $ - عدد المراحل. وهنا تظهر المهمة ، كيف تعرف فقط كتل جميع أنواع أجزاء أي جزيء ، لمعرفة هيكلها؟ لذلك جئنا إلى مشاكل البكرات والممرات ، بالنسبة للببتيدات الخطية والدورية ، على التوالي.

سأشرح بمزيد من التفصيل كيف يتم تقليل مهمة استعادة بنية الجزيء الحيوي إلى المشاكل المشار إليها باستخدام مثال الببتيد الدوري.



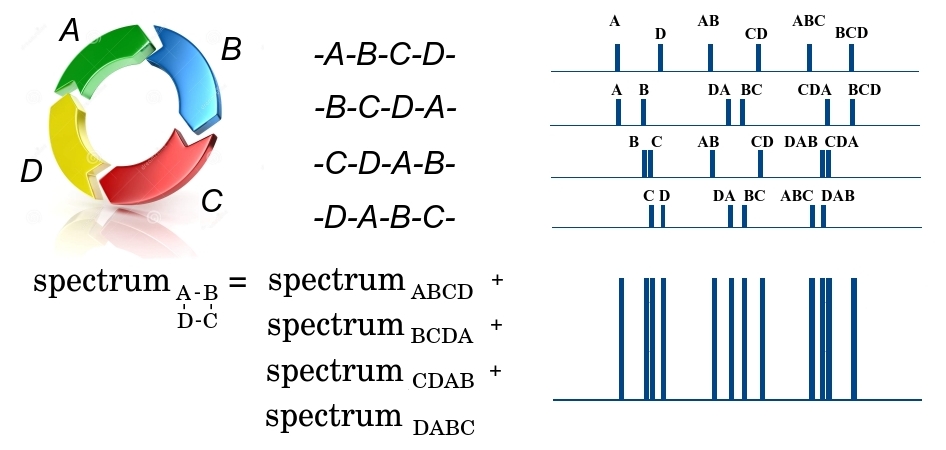
يمكن كسر الببتيد الحلقي ABCD في المرحلة الأولى من التجزئة في 4 أماكن ، إما عن طريق ارتباط DA ، أو عن طريق AB أو BC أو CD ، لتشكيل 4 ببتيدات خطية محتملة - إما ABCD أو BCDA أو CDAB أو DABC. نظرًا لأن عددًا كبيرًا من الببتيدات المتطابقة يمر عبر مطياف ، سيكون لدينا شظايا من جميع الأنواع الأربعة عند الإخراج. علاوة على ذلك ، نلاحظ أن جميع الأجزاء لها نفس الكتلة ، ولا يمكن فصلها في المرحلة الأولى. في المرحلة الثانية ، يمكن كسر الجزء الخطي ABCD في ثلاثة أماكن ، وتشكيل أجزاء أصغر بكتل مختلفة A و BCD ، AB و CD ، ABC و D ، وتشكيل الطيف الكتلي المقابل. في هذا الطيف ، يتم رسم كتلة الشظية على طول المحور س ، وعدد الأجزاء الصغيرة مع كتلة معينة على طول المحور ص. وبالمثل ، تتشكل الأطياف للأجزاء الخطية الثلاثة المتبقية من BCDA و CDAB و DABC. نظرًا لتمرير جميع الأجزاء الأربعة الكبيرة إلى المرحلة الثانية ، تتم إضافة جميع أطيافها. المجموع ، النتيجة هي بعض الكتلة$$ $ inline $ \ {m_1 ^ {n_1} ، m_2 ^ {n_2} ، .. ، m_q ^ {n_q} \} $ مضمنة $ أين$$ $ inline $ m_i $ مضمنة $ - بعض الكتلة و$$ $ inline $ n_i $ مضمنة $ - تكرار تكرارها. في الوقت نفسه ، لا نعرف إلى أي جزء تنتمي هذه الكتلة وما إذا كانت هذه القطعة فريدة ، لأن الأجزاء المختلفة يمكن أن يكون لها كتلة واحدة. كلما كانت الروابط في الببتيد أبعد من بعضها البعض ، كلما زادت كتلة جزء الببتيد بينهما. أي أن مهمة استعادة ترتيب العناصر في الببتيد الدوري تقلل من مشكلة الحزام ، حيث تكون عناصر المجموعة$$ $ مضمنة $ X $ مضمنة $ هي روابط في الببتيد وعناصر للجمهور$$ $ inline $ \ Delta X $ inline $ - كتل الشظايا بين السندات.

توقع وجود خوارزمية ذات وقت متعدد الحدود لحل مشاكل الحزام

من تجربتي الخاصة ومن التواصل مع الأشخاص الذين حاولوا أو فعلوا شيئًا بالفعل لحل هذه المشكلة ، لاحظت أن الغالبية العظمى من الأشخاص يحاولون حلها إما في الحالة العامة أو للبيانات الصحيحة في نطاق ضيق ، مثل هذا (1 ، 50). كلا الخيارين محكوم عليهما بالفشل. بالنسبة للحالة العامة ، تم إثبات أن العدد الإجمالي للحلول لمشاكل الحزام في الحالة أحادية البعد$$ $ مضمنة $ S_1 (n) $ مضمنة $ مقيدة بالقيم (Lemke ، 2003)

$$$$ display $$ e ^ {2 ^ {\ frac {\ ln n} {\ ln \ ln n} + o (1)}} \ leq S_1 (n) \ leq \ frac {1} {2} n ^ {n-2} $$ display $$

وهو ما يعني وجود عدد أسي من الحلول في الخطوط المقاربة$$ $ inline $ n \ rightarrow \ infty $ inline $ . من الواضح أنه إذا كان عدد الحلول ينمو بشكل كبير ، فإن وقت استلامها لا يمكن أن ينمو بشكل أبطأ. أي أنه بالنسبة للحالة العامة ، من المستحيل الحصول على حل زمني متعدد الحدود. أما بالنسبة للبيانات الصحيحة في النطاق الضيق ، فيمكن التحقق من كل شيء تجريبيًا ، لأنه ليس من الصعب جدًا كتابة التعليمات البرمجية التي تبحث عن حل عن طريق البحث الشامل. للصغار$$ $ مضمنة $ n $ مضمنة $ مثل هذا الرمز لن يستغرق وقتًا طويلاً. ستظهر نتائج الاختبار لمثل هذا الرمز أنه في ظل ظروف البيانات هذه ، يكون إجمالي عدد الحلول المختلفة لأي مجموعة$$ $ inline $ \ Delta X $ inline $ بالفعل صغيرة$$ $ مضمنة $ n $ مضمنة $ ينمو بشكل حاد للغاية.

بعد التعرف على هذه الحقائق ، يمكنك طرح هذه المهمة والتخلي عنها. أعترف أن هذا هو أحد الأسباب التي تجعل مشكلة الحزام لا تزال بدون حل. ومع ذلك ، توجد ثغرات. أذكر أن الدالة الأسية$$ $ inline $ e ^ {\ alpha x} $ مضمنة $ يتصرف بشكل مثير للاهتمام. في البداية ، تنمو ببطء شديد ، وترتفع من 0 إلى 1 على مدى فترة زمنية غير محدودة من$$ $ مضمنة $ \ infty $ مضمنة $ إلى 0 ، ثم تسارع نموه أكثر وأكثر. ومع ذلك ، كلما انخفضت القيمة$$ $ مضمنة $ \ alpha $ مضمنة $ كلما زادت القيمة$$ $ مضمنة $ x $ مضمنة $ بحيث تتخطى نتيجة الدالة بعض القيمة المحددة$$ $ inline $ y = \ xi $ مضمنة $ . على هذا النحو ، من المناسب اختيار رقم$$ $ inline $ \ xi = 2 $ inline $ أمامه الحل الوحيد ، وبعده قرارات كثيرة. سؤال وهل قام أي شخص بالتحقق من اعتماد عدد القرارات على البيانات التي يتم إدخالها إلى الإدخال؟ نعم فعلت. هناك أطروحة دكتوراه رائعة من قبل عالم الرياضيات الكرواتي تمارا داكيس (داكيك ، 2000) ، والتي حددت فيها الشروط التي يجب أن تفي بها بيانات الإدخال من أجل حل المشكلة في وقت متعدد الحدود. وأهمها تفرد الحل وغياب الازدواجية في مجموعة بيانات الإدخال.$$ $ inline $ \ Delta X $ inline $ . مستوى أطروحة الدكتوراه مرتفع للغاية. من المؤسف أن هذه الطالبة اقتصرت على مشكلة دوران فقط ، وأنا مقتنع بأنها لو حولت اهتمامها بمشكلة الحزام ، لكان قد تم حلها لفترة طويلة.

الحصول على خوارزمية مع حل متعدد الحدود لحل مشاكل الحزام

كان من الممكن العثور على البيانات التي من الممكن بناء الخوارزمية المطلوبة عن طريق الصدفة. استغرق الأمر أفكارًا إضافية. نشأت الفكرة الرئيسية من الملاحظة (انظر أعلاه) أن طيف الببتيد الدوري هو مجموع أطياف جميع الببتيدات الخطية التي تتشكل عند استراحات الحلقة الواحدة. بما أن تسلسل الأحماض الأمينية في الببتيد يمكن استعادته من أي ببتيد خطي ، فإن العدد الإجمالي للخطوط في الطيف مهم (في$$ $ مضمنة $ n $ مضمنة $ مرات أين$$ $ مضمنة $ n $ مضمنة $ - عدد الأحماض الأمينية في الببتيد) مفرط. السؤال هو فقط الخطوط التي يجب استبعادها من الطيف حتى لا تفقد القدرة على استعادة التسلسل. بما أن كلتا المهمتين (استعادة تسلسل الببتيد الدوري من مشكلة الطيف الكتلي ومشكلة الحزام) هي متشابهة رياضيًا ، فمن الممكن أيضًا تخفيف الكثير$$ $ inline $ \ Delta X $ inline $ .

عمليات التخفيف$$ $ inline $ \ Delta X $ inline $ تم إنشاؤها باستخدام التماثلات المحلية للمجموعة$$ $ inline $ \ Delta X $ inline $ (فومين ، 2016 أ).

• التماثل العملية الأولى هي تحديد عنصر تعسفي للمجموعة$$ $ inline $ x _ {\ mu} \ in \ Delta X $ مضمنة $ وإزالتها من$$ $ inline $ \ Delta X $ inline $ جميع العناصر باستثناء تلك التي لها أزواج متناظرة فيما يتعلق بالنقاط$$ $ inline $ x _ {\ mu} / 2 $ $ مضمنة و$$ $ inline $ (L + x _ {\ mu}) / 2 $ مضمنة $ أين$$ $ مضمنة $ L $ مضمنة $ - محيط (أذكر أنه في حالة الحزام ، تقع جميع النقاط على الدائرة).
• الالتفاف الحل الجزئي. تستخدم العملية الثانية التخمين حول الحل ، أي معرفة النقاط الفردية التي تنتمي إلى الحل ، ما يسمى بالحل الجزئي. من بين الكثير$$ $ inline $ \ Delta X $ inline $ يتم أيضًا حذف جميع العناصر ، باستثناء تلك التي تستوفي الشرط - إذا قمنا بقياس المسافة من النقطة التي يتم اختبارها إلى جميع نقاط الحل الجزئي ، فإن جميع القيم التي تم الحصول عليها تكون في$$ $ inline $ \ Delta X $ inline $ . سأوضح أنه في حالة عدم وجود مسافة واحدة على الأقل من المسافات التي تم الحصول عليها$$ $ inline $ \ Delta X $ inline $ ثم يتم تجاهل النقطة.

أثبتت النظريات أن كلتا العمليتين تضعف المجموعة$$ $ inline $ \ Delta X $ inline $ ، ولكن لا يزال لديها عناصر كافية لاستعادة الحل$$ $ مضمنة $ X $ مضمنة $ . باستخدام هذه العمليات ، تم بناء خوارزمية وتنفيذها في c ++ لحل مشكلة الحزام (Fomin، 2016b). تختلف الخوارزمية قليلاً عن خوارزمية التراجع الكلاسيكية (أي أننا نحاول بناء حل من خلال تعداد الخيارات الممكنة والعودة إذا حصلنا على خطأ أثناء البناء). والفرق الوحيد هو أن تضيق المجموعة$$ $ inline $ \ Delta X $ inline $ لاختبارنا يصبح خيارات أقل بكثير.

إليك مثال عن العدد$$ $ inline $ \ Delta X $ inline $ عند الترقق.



أجريت تجارب حسابية على الببتيدات الحلقية ذات الطول العشوائي$$ $ مضمنة $ n $ مضمنة $ من 10 إلى 1000 من الأحماض الأمينية (المحور الإحداثي على مقياس لوغاريتمي). تظهر الخراج أيضًا على مقياس لوغاريتمي عدد العناصر في المجموعات التي خففتها العمليات المختلفة$$ $ inline $ \ Delta X $ inline $ في الوحدات$$ $ مضمنة $ n $ مضمنة $ . مثل هذا التمثيل غير معتاد على الإطلاق ، لذلك سأفهم كيفية قراءته على سبيل المثال. نحن ننظر إلى المخطط الأيسر. دع الببتيد له طول$$ $ inline $ n = $ 100 مضمنة $ . بالنسبة له ، عدد العناصر في المجموعة$$ $ inline $ \ Delta X $ inline $ يساوي$$ $ مضمنة $ n ^ 2 = 10000 $ مضمنة $ (هذه نقطة على الخط المتقطع العلوي$$ $ inline $ y = n ^ 2 $ inline $ ) بعد الإزالة من المجموعة$$ $ inline $ \ Delta X $ inline $ تكرار العناصر ، عدد العناصر في$$ $ inline $ \ Delta X $ inline $ يقلل$$ $ inline $ n_D \ تقريبا ن ^ {1.9} \ تقريبا 6300 $ مضمنة $ (دوائر بصلبان). بعد التماثل ينخفض ​​عدد العناصر إلى$$ $ inline $ n_S \ تقريبا n ^ {1.75} \ حوالي 3100 $ $ مضمنة (الدوائر السوداء) ، وبعد الالتفاف بحل جزئي ل$$ $ inline $ n_C \ تقريبا ن ^ {1.35} \ حوالي 500 $ مضمنة $ (الصلبان). الإجمالي ، إجمالي حجم المجموعة$$ $ inline $ \ Delta X $ inline $ خفضت 20 مرة فقط. بالنسبة للببتيد من نفس الطول ، ولكن في الرسم البياني الأيمن ، يأتي الانكماش$$ $ مضمنة $ n ^ 2 = 10000 $ مضمنة $ من قبل$$ $ inline $ N_C \ تقريبا n \ تقريبا $ 100 مضمنة $ ، أي 100 مرة.

لاحظ أنه يتم تنفيذ توليد حالات الاختبار للرسم الأيسر بحيث يكون مستوى الازدواجية$$ $ inline $ k_ {dup} $ مضمنة $ في$$ $ inline $ \ Delta X $ inline $ كان في النطاق من 0.1 إلى 0.3 ، ولليمين - أقل من 0.1. يتم تعريف مستوى الازدواجية على أنه$$ $ inline $ k_ {dup} = 2- \ log {N_u} / \ log {n} $ inline $ أين$$ $ مضمنة $ N_u $ مضمنة $ - عدد العناصر الفريدة في المجموعة$$ $ inline $ \ Delta X $ inline $ . يعطي هذا التعريف نتيجة طبيعية: في غياب التكرارات في المجموعة$$ $ inline $ \ Delta X $ inline $ قوتها متساوية$$ $ inline $ N_u = n ^ 2 $ $ inline $ و$$ $ inline $ k_ {dup} = 0 $ $ مضمنة بأقصى قدر ممكن من الازدواجية$$ $ inline $ N_u = n $ مضمنة $ و$$ $ inline $ k_ {dup} = 1 $ $ مضمنة . كيفية جعل من الممكن توفير مستوى مختلف من الازدواجية ، سأقول بعد ذلك بقليل. تظهر الرسوم البيانية أنه كلما انخفض مستوى الازدواجية ، كلما كان أرق$$ $ inline $ \ Delta X $ inline $ في$$ $ inline $ k_ {dup} <0.1 $ inline $ عدد العناصر في ضعيفة$$ $ inline $ \ Delta X $ inline $ بشكل عام يصل إلى حده$$ $ inline $ O (n ^ 2) \ rightarrow O (n) $ inline $ ، لأنه في المجموعة المهلكة أقل من$$ $ inline $ O (n) $ مضمنة $ لا يمكن الحصول على العناصر (تخزن العمليات عناصر كافية للحصول على حل فيه$$ $ مضمنة $ n $ مضمنة $ العناصر). حقيقة تضييق قوة المجموعة$$ $ inline $ \ Delta X $ inline $ إلى الحد الأدنى مهم جدًا ، فهو الذي يؤدي إلى تغييرات جذرية في التعقيد الحسابي للحصول على حل.

بعد إدخال عمليات التخفيف في خوارزمية التراجع وحل مشكلة الحزام ، تم الكشف عن تناظرية كاملة لما تحدثت عنه تمارا داكيس فيما يتعلق بمشكلة الدوران. دعني أذكرك. وقالت أنه بالنسبة لمشاكل الدوران ، من الممكن الحصول على حل في وقت كثير الحدود إذا كان الحل فريدًا وليس هناك ازدواجية في$$ $ inline $ \ Delta X $ inline $ . اتضح أن الغياب التام للازدواج ليس ضروريًا (من الصعب جدًا الحصول على بيانات حقيقية) ، يكفي أن يكون مستواه صغيرًا جدًا. يوضح الشكل أدناه مقدار الوقت المطلوب للحصول على حل لمشكلة الحزام اعتمادًا على طول الببتيد ومستوى الازدواجية في$$ $ inline $ \ Delta X $ inline $ .



في الشكل ، يتم إعطاء كل من الإحداثي والإحداثيات على مقياس لوغاريتمي. هذا يسمح لك أن ترى بوضوح ما إذا كان الاعتماد على وقت العد على طول التسلسل$$ $ inline $ T = f (n) $ مضمنة $ أسي (خط مستقيم) أو متعدد الحدود (منحنى شكل السجل). كما يمكن رؤيته في المخططات ، مع مستوى منخفض من الازدواجية (المخطط الأيمن) ، يتم الحصول على الحل في وقت كثير الحدود. حسنًا ، لنكون أكثر دقة ، يتم الحصول على الحل في الوقت التربيعي. يحدث هذا عندما تقلل عمليات التخفيف من قوة المجموعة إلى حد أدنى.$$ $ inline $ O (n ^ 2) \ rightarrow O (n) $ inline $ ، هناك نقاط قليلة متبقية فيه ، تعود عندما يصبح التكرار على الخيارات مفردة ، وفي جوهرها تتوقف الخوارزمية عن تكرار الخيارات ، ولكنها ببساطة تبني حلًا مما يتبقى.

PS حسنا ، سأكشف عن السر الأخير فيما يتعلق بإنشاء مجموعات على مستويات مختلفة من الازدواجية. هذا يرجع إلى اختلاف دقة عرض البيانات. إذا تم إنشاء البيانات بدقة منخفضة (على سبيل المثال ، التقريب إلى أعداد صحيحة) ، يصبح مستوى التكرار مرتفعًا ، أكثر من 0.3. , , 3 , , 0.1. .

, , beltway .


.

1. Dakic, T. (2000). On the Turnpike Problem. PhD thesis, Simon Fraser University.
2. Fomin. E. (2016a) A Simple Approach to the Reconstruction of a Set of Points from the Multiset of n^2 Pairwise Distances in n^2 Steps for the Sequencing Problem: I. Theory. J Comput Biol. 2016, 23(9):769-75.
3. Fomin. E. (2016b) A Simple Approach to the Reconstruction of a Set of Points from the Multiset of n^2 Pairwise Distances in n^2 Steps for the Sequencing Problem: II. Algorithm. J Comput Biol. 2016, 23(12):934-942.
4. Lemke, P., Skiena, S., and Smith, W. (2003). Reconstructing Sets From Interpoint Distances. Discrete and Computational Geometry Algorithms and Combinatorics, 25:597–631.
5. Skiena, S., Smith, W., and Lemke, P. (1990). Reconstructing sets from interpoint distances. In Proceedings of the Sixth ACM Symposium on Computational Geometry, pages 332–339. Berkeley, CA
6. Zhang, Z. 1982. An exponential example for a partial digest mapping algorithm. J. Comp. Biol. 1, 235–240.