تنفيذ خوارزمية k- الوسائل (k-الوسائل) باستخدام مثال العمل بالبكسل

مرحبا بالجميع! في الآونة الأخيرة ، كان من الضروري كتابة تعليمات برمجية لتنفيذ تجزئة الصورة باستخدام طريقة k-الوسائل (الوسائل الإنجليزية k). حسنًا ، أول شيء تفعله Google هو المساعدة. لقد عثرت على الكثير من المعلومات ، مثل من وجهة نظر رياضية (جميع أنواع الخربشات الرياضية المعقدة هناك ، ستفهم ما هو مكتوب هناك) ، بالإضافة إلى بعض تطبيقات البرامج الموجودة على الإنترنت باللغة الإنجليزية. هذه الرموز جميلة بالتأكيد - لا شك ، ولكن من الصعب فهم جوهر الفكرة. بطريقة ما ، كل شيء معقد هناك ، مرتبك ، ومع ذلك ، باليد ، لن تكتب الرمز ، لن تفهم أي شيء. في هذه المقالة ، أريد أن أعرض تنفيذًا بسيطًا وليس منتجًا ، ولكن آمل أن يكون مفهوما لهذه الخوارزمية الرائعة. حسنًا ، لنذهب!

إذن ما هو التجمع من حيث تصوراتنا؟ دعني أعطيك مثالاً ، لنفترض أن هناك صورة جميلة بالزهور من منزل جدتك.



السؤال هو: لتحديد عدد المناطق في هذه الصورة المملوءة بنفس اللون تقريبًا. حسنًا ، الأمر ليس صعبًا على الإطلاق: بتلات بيضاء - واحدة ، مراكز صفراء - اثنان (أنا لست عالم أحياء ، لا أعرف ما يطلق عليهما) ، ثلاث خضر. تسمى هذه الأقسام العناقيد. الكتلة هي مجموعة من البيانات التي لها ميزات مشتركة (اللون والموضع وما إلى ذلك). تسمى عملية تحديد ووضع كل مكون من أي بيانات في هذه المجموعات - المقاطع التجميع.

هناك العديد من خوارزميات التجميع ، ولكن أبسطها هو k - متوسط ​​، والذي سيتم مناقشته لاحقًا. K-يعني خوارزمية بسيطة وفعالة يسهل تنفيذها باستخدام طريقة برمجية. البيانات التي سنقوم بتوزيعها في مجموعات هي بكسل. كما تعلم ، يحتوي بكسل الألوان على ثلاثة مكونات - الأحمر والأخضر والأزرق. فرض هذه المكونات وإنشاء لوحة من الألوان الموجودة.



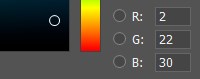
في ذاكرة الكمبيوتر ، يتميز كل مكون لون برقم من 0 إلى 255. أي أنه يجمع بين قيم مختلفة من الأحمر والأخضر والأزرق ، نحصل على لوحة ألوان على الشاشة.

باستخدام وحدات البكسل كمثال ، نقوم بتنفيذ الخوارزمية الخاصة بنا. K- يعني خوارزمية تكرارية ، أي أنها ستعطي النتيجة الصحيحة ، بعد عدد معين من التكرار لبعض الحسابات الرياضية.

خوارزمية

1. يجب أن تعرف مقدمًا عدد المجموعات التي تحتاجها لتوزيع البيانات. يعد هذا عيبًا كبيرًا لهذه الطريقة ، ولكن يتم حل هذه المشكلة من خلال التطبيقات المحسنة للخوارزمية ، ولكن هذه ، كما يقولون ، قصة مختلفة تمامًا.
2. نحن بحاجة إلى اختيار المراكز الأولية لمجموعاتنا. كيف؟ نعم بشكل عشوائي. لماذا؟ بحيث يمكنك انجذاب كل بكسل إلى مركز الكتلة. المركز مثل الملك ، حيث يتم تجميع رعاياه - بكسل. إن "المسافة" من المركز إلى البكسل هي التي تحدد لمن تطيعه كل بكسل.
3. نحسب المسافة من كل مركز إلى كل بكسل. تعتبر هذه المسافة هي المسافة الإقليدية بين النقاط في الفضاء ، وفي حالتنا ، المسافة بين مكونات الألوان الثلاثة:

   $$$$ display $$ \ sqrt {(R_ {2} -R_ {1}) ^ 2 + (G_ {2} -G_ {1}) ^ 2 + (B_ {2} -B_ {1}) ^ 2} . $$ display $$

   نحسب المسافة من البكسل الأول إلى كل مركز ونحدد أصغر مسافة بين هذه البكسل والمراكز. بالنسبة للمركز ، والمسافة التي هي أصغرها ، نقوم بإعادة حساب الإحداثيات كمتوسط ​​حسابي بين كل مكون من عناصر البكسل - الملك والبكسل - للموضوع. يتغير مركزنا في الفضاء وفقًا للحسابات.
4. بعد إعادة سرد جميع المراكز ، نقوم بتوزيع وحدات البكسل في مجموعات ، ومقارنة المسافة من كل بكسل إلى المراكز. يتم وضع البكسل في كتلة ، يكون مركزها أقرب منه إلى المراكز الأخرى.
5. يبدأ كل شيء مرة أخرى ، طالما بقيت البكسل في نفس العناقيد. غالبًا ما لا يحدث هذا ، نظرًا لأن كمية كبيرة من البيانات ستتحرك المراكز في نصف قطر صغير ، وستقفز وحدات البكسل على طول حواف المجموعات إلى مجموعة أو أخرى. للقيام بذلك ، حدد الحد الأقصى لعدد التكرارات.

التنفيذ

سأقوم بتنفيذ هذا المشروع في C ++. الملف الأول هو "k_means.h" ، حيث قمت بتعريف أنواع البيانات الرئيسية والثوابت والفئة الرئيسية للعمل - "K_means".
لتمييز كل بكسل ، قم بإنشاء هيكل يتكون من ثلاثة مكونات بكسل ، اخترت النوع المزدوج لها لإجراء حسابات أكثر دقة ، كما حددت بعض الثوابت ليعمل البرنامج:

const int KK = 10; //  const int max_iterations = 100; //   typedef struct { double r; double g; double b; } rgb; 

K_ يعني الصف نفسه:

 class K_means { private: std::vector<rgb> pixcel; int q_klaster; int k_pixcel; std::vector<rgb> centr; void identify_centers(); inline double compute(rgb k1, rgb k2) { return sqrt(pow((k1.r - k2.r),2) + pow((k1.g - k2.g), 2) + pow((k1.b - k2.b), 2)); } inline double compute_s(double a, double b) { return (a + b) / 2; }; public: K_means() : q_klaster(0), k_pixcel(0) {}; K_means(int n, rgb *mas, int n_klaster); K_means(int n_klaster, std::istream & os); void clustering(std::ostream & os); void print()const; ~K_means(); friend std::ostream & operator<<(std::ostream & os, const K_means & k); }; 

لنستعرض مكونات الفصل:

vectorpixcel - ناقل للبكسل ؛
q_klaster - عدد العناقيد ؛
k_pixcel - عدد البكسل ؛
Vectorcentr - متجه لمراكز التجميع ، يتم تحديد عدد العناصر فيه بواسطة q_klaster ؛
Ident_centers () - طريقة لاختيار المراكز الأولية عشوائيًا بين وحدات بكسل الإدخال ؛
compute () و compute_s () طريقتان مدمجتان لحساب المسافة بين البكسل ومراكز إعادة الحساب ، على التوالي ؛
ثلاثة مُنشئات: الأول بشكل افتراضي ، والثاني هو لتهيئة وحدات البكسل من مصفوفة ، والثالث لتهيئة وحدات البكسل من ملف نصي (في التطبيق الخاص بي ، يتم تعبئة الملف عن طريق الخطأ بالبيانات في البداية ، ثم تتم قراءة وحدات البكسل من هذا الملف لكي يعمل البرنامج ، لماذا لا مباشرة إلى المتجه - مطلوب فقط في حالتي) ؛
التجمع (std :: ostream & os) - طريقة التجميع ؛
طريقة وحمل بيان المخرجات الزائد لنشر النتائج.

تنفيذ الأسلوب:

 void K_means::identify_centers() { srand((unsigned)time(NULL)); rgb temp; rgb *mas = new rgb[q_klaster]; for (int i = 0; i < q_klaster; i++) { temp = pixcel[0 + rand() % k_pixcel]; for (int j = i; j < q_klaster; j++) { if (temp.r != mas[j].r && temp.g != mas[j].g && temp.b != mas[j].b) { mas[j] = temp; } else { i--; break; } } } for (int i = 0; i < q_klaster; i++) { centr.push_back(mas[i]); } delete []mas; } 

هذه طريقة لاختيار مراكز التجميع الأولية وإضافتها إلى ناقل المركز. يتم إجراء فحص لتكرار المراكز واستبدالها في هذه الحالات.

 K_means::K_means(int n, rgb * mas, int n_klaster) { for (int i = 0; i < n; i++) { pixcel.push_back(*(mas + i)); } q_klaster = n_klaster; k_pixcel = n; identify_centers(); } 

تطبيق منشئ لتهيئة وحدات البكسل من صفيف.

 K_means::K_means(int n_klaster, std::istream & os) : q_klaster(n_klaster) { rgb temp; while (os >> temp.r && os >> temp.g && os >> temp.b) { pixcel.push_back(temp); } k_pixcel = pixcel.size(); identify_centers(); } 

نقوم بتمرير كائن إدخال إلى هذا المُنشئ حتى نتمكن من إدخال البيانات من كل من الملف ووحدة التحكم.

 void K_means::clustering(std::ostream & os) { os << "\n\n :" << std::endl; /*             :        ,    -  ,    ,   ,        .*/ std::vector<int> check_1(k_pixcel, -1); std::vector<int> check_2(k_pixcel, -2); int iter = 0; /* .*/ while(true) { os << "\n\n----------------  №" << iter << " ----------------\n\n"; { for (int j = 0; j < k_pixcel; j++) { double *mas = new double[q_klaster]; /*  :          .      ,   .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[j], centr[i]); os << "   " << j << "   #" << i << ": " << *(mas + i) << std::endl; } /*     m_k      .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } os << "    #" << m_k << std::endl; os << "  #" << m_k << ": "; centr[m_k].r = compute_s(pixcel[j].r, centr[m_k].r); centr[m_k].g = compute_s(pixcel[j].g, centr[m_k].g); centr[m_k].b = compute_s(pixcel[j].b, centr[m_k].b); os << centr[m_k].r << " " << centr[m_k].g << " " << centr[m_k].b << std::endl; delete[] mas; } /*   .*/ int *mass = new int[k_pixcel]; os << "\n  : "<< std::endl; for (int k = 0; k < k_pixcel; k++) { double *mas = new double[q_klaster]; /*    .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[k], centr[i]); os << "   №" << k << "   #" << i << ": " << *(mas + i) << std::endl; } /*  .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } mass[k] = m_k; os << " №" << k << "     #" << m_k << std::endl; } /*            .*/ os << "\n    : \n"; for (int i = 0; i < k_pixcel; i++) { os << mass[i] << " "; check_1[i] = *(mass + i); } os << std::endl << std::endl; os << " : " << std::endl; int itr = KK + 1; for (int i = 0; i < q_klaster; i++) { os << " #" << i << std::endl; for (int j = 0; j < k_pixcel; j++) { if (mass[j] == i) { os << pixcel[j].r << " " << pixcel[j].g << " " << pixcel[j].b << std::endl; mass[j] = ++itr; } } } delete[] mass; /*    .*/ os << " : \n" ; for (int i = 0; i < q_klaster; i++) { os << centr[i].r << " " << centr[i].g << " " << centr[i].b << " - #" << i << std::endl; } } /*         –  .*/ iter++; if (check_1 == check_2 || iter >= max_iterations) { break; } check_2 = check_1; } os << "\n\n ." << std::endl; } 

الطريقة الرئيسية للتجميع.

 std::ostream & operator<<(std::ostream & os, const K_means & k) { os << " : " << std::endl; for (int i = 0; i < k.k_pixcel; i++) { os << k.pixcel[i].r << " " << k.pixcel[i].g << " " << k.pixcel[i].b << " - №" << i << std::endl; } os << std::endl << "   : " << std::endl; for (int i = 0; i < k.q_klaster; i++) { os << k.centr[i].r << " " << k.centr[i].g << " " << k.centr[i].b << " - #" << i << std::endl; } os << "\n : " << k.q_klaster << std::endl; os << " : " << k.k_pixcel << std::endl; return os; } 

إخراج البيانات الأولية.

مثال الإخراج

تم التخطيط لهذا المثال مسبقًا ، ويتم تحديد وحدات البكسل خصيصًا للتوضيح. يكفي تكراران للبرنامج لتجميع البيانات في ثلاث مجموعات. بالنظر إلى مراكز التكررين الماضيين ، يمكنك أن ترى أنها بقيت في مكانها عمليًا.

أكثر إثارة للاهتمام هي حالات بكسل تم إنشاؤها بشكل عشوائي. بعد أن ولدت 50 نقطة يجب تقسيمها إلى 10 مجموعات ، حصلت على 5 تكرارات. بعد أن ولدت 50 نقطة يجب تقسيمها إلى 3 مجموعات ، حصلت على كل 100 تكرار كحد أقصى مسموح به. قد تلاحظ أنه كلما زاد عدد المجموعات ، كان من الأسهل على البرنامج العثور على وحدات البكسل الأكثر تشابهًا ودمجها في مجموعات أصغر ، والعكس صحيح - إذا كان هناك عدد قليل من المجموعات وهناك العديد من النقاط ، غالبًا ما تنتهي الخوارزمية فقط عندما يتم تجاوز الحد الأقصى لعدد التكرارات ، حيث تقفز بعض وحدات البكسل باستمرار من عنقود لآخر. ومع ذلك ، لا يزال الجزء الأكبر محددًا في مجموعاته بالكامل.

حسنًا ، الآن دعنا نتحقق من نتيجة التجميع. بأخذ نتيجة بعض المجموعات من مثال 50 نقطة لكل 10 مجموعات ، قمت بقيادة نتيجة هذه البيانات إلى Illustrator وهذا ما حدث:



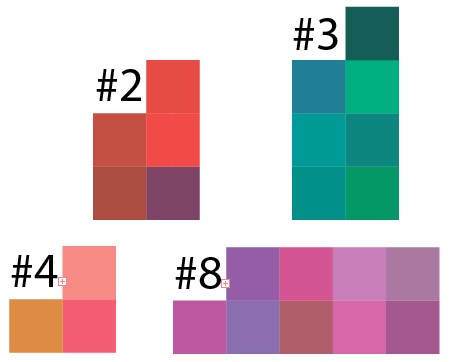
يمكن ملاحظة أنه في كل مجموعة تسود أي ظلال من الألوان ، وهنا تحتاج إلى فهم أنه تم اختيار وحدات البكسل بشكل عشوائي ، فإن التناظرية لمثل هذه الصورة في الحياة الواقعية هي نوع من الصورة التي يتم رش جميع الألوان عليها عن طريق الخطأ ومن الصعب تحديد مناطق ذات ألوان متشابهة.

لنفترض أن لدينا مثل هذه الصورة. يمكننا تعريف الجزيرة على أنها كتلة واحدة ، ولكن مع زيادة نرى أنها تتكون من ظلال مختلفة من اللون الأخضر.



وهذه هي المجموعة 8 ، ولكن في نسخة أصغر ، تكون النتيجة متشابهة:



يمكن الاطلاع على النسخة الكاملة من البرنامج على GitHub .