رياضيات مسلية. نظام الأرقام الأكثر اقتصادا

نعلم جميعًا من الدورة الدراسية ما هو نظام الأرقام (SS). لكن لا يفكر الجميع في مقدار SS. على سبيل المثال ما مجموعة الأرقام التي نحتاجها لتمثيل الرقم في SS هذا. عندما يكون لدينا مجموعة محدودة من العناصر الفريدة (الحصى متعددة الألوان بأحجام مختلفة) والتي يمكننا من خلالها تمثيل عدد ، ما هو أقصى عدد يمكننا تمثيله باستخدام هذه العناصر؟ (جميع الحصى الحمراء صفر ، والأخضر واحد ، والأزرق اثنان ، وما إلى ذلك ، والصغير صفر ، المتوسط ​​أولاً ، كبير الثاني ، إلخ.). أين هو الخط الذي تلعب فيه قاعدة SS دورًا أكبر من سعة الرقم؟

خذ على سبيل المثال n - عدد العناصر يساوي 60. بعد تقسيم العناصر إلى مجموعتين (نظام الأرقام الثنائية) نحصل على 30 رقمًا. 30 وحدة هو أكبر رقم 30 بت مع قاعدة من 2. إذا أضفت 1 إليه ، تحصل على وحدة تحتوي على 30 أصفار ، أي 2 في 30 ، حيث أن كل صفر هو قوة من اثنين ، وتبدأ الأرقام عند 0 ، ولا تنسَ طرح الوحدة التي تمت إضافتها.

بالنسبة إلى SSs الأخرى ، بالمثل $$$y = x ^ {60 / x} -1$ حيث y هي العدد الأقصى ، x هي أساس الدرجة.

نقاط البناء:

$$$2 ^ {30} -1 = 1 \، 073 \، 741 \، 823$ .
$$$3 ^ {20} -1 = 3 \، 486 \، 784 \، 400$ .
$$$4 ^ {15} -1 = 1 \، 073 \، 741 \، 823$
$$$5 ^ {12} -1 = 244 \، 140 \، 624$
$$
$$$10 ^ {6} -1 = 999 \ ، 999 دولارً$
$$

الرسم البياني للدالة:



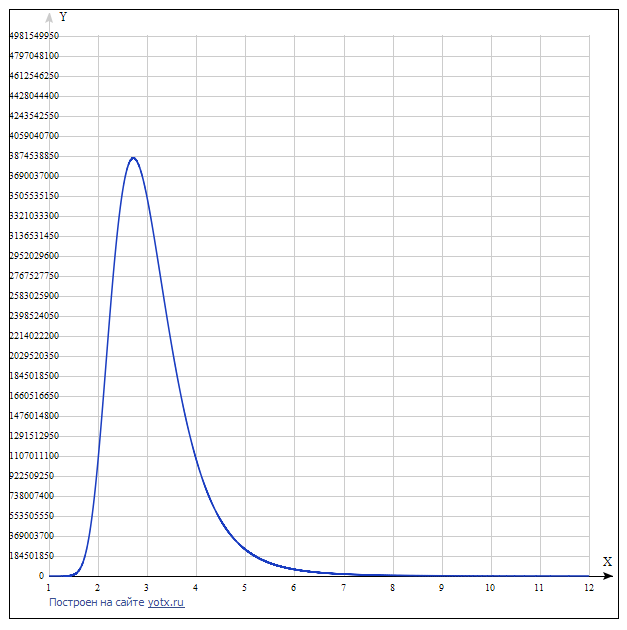
يوضح الرسم البياني أنه مع زيادة قاعدة SS ، بدءًا من ثلاثة ، تزداد تكلفتها والوظيفة لها أقصى تطرف. جعله في شكل عام ، يمكنك الحصول عليه $$$y = (\ sqrt [x] x) ^ {n} -1$ ، والوظيفة القصوى $$$\ sqrt [x] x$ يتحقق عندما $$$x = e$ .



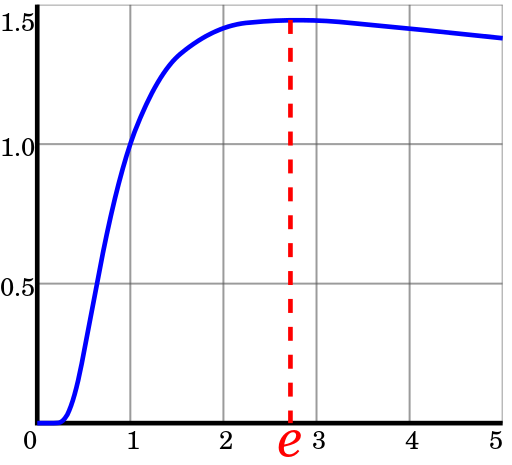
الرسم البياني للدالة $$$y = \ sqrt [x] x$

على سبيل المثال الأكثر اقتصادا SS هو نظام أقرب ما يكون إلى $$$e$ أو 3.

ملاحظة: بالإضافة إلى ذلك ، فإن SS مع الأساس 3 غريب ، مما يعني أنه ليس لديه مشكلة في التقريب (إحضار 0.5 إلى 0 أو إلى 1) ، وإذا كانت الأرقام مكتوبة بشكل متماثل (-1.0.1 بدلاً من 0.1.2) ، فستظهر البساطة تمثل الأرقام السالبة (10-1 هي 8 ، -101 هي -8 ، حيث لا يكون الطرح علامة ، بل جزء من رقم يمكن استبداله بـ Z) ، ولكن هذا حساب مختلف تمامًا)))