الماكرة البادئة شجرة تنفيذ C

مقدمة

لقد مرت أربعة أشهر منذ نشر المقال حول محاولتي في تنفيذ منخفض المستوى لشجرة البادئة . على الرغم من كل جهودي ، فإن السقف الذي اتضح أن تنفيذي السابق لشجرة البادئة كان قادرًا عليه كان ~ 80 ألف كلمة في الثانية. ثم قضيت الكثير من الوقت والطاقة ، ولكن النتيجة ستكون مناسبة فقط للعمل المخبري في علوم الكمبيوتر.

ثم أخبرني الكثيرون: "لا تخترع دراجة اخترعناها بالفعل! استخدم الحل الجاهز. " الصعوبة هي أنني لم أستطع استخدام شيء لا أفهمه على الأقل بعبارات عامة.

أعتقد أنني فهمت شجرة البادئة ، وهذا ما تمكنت من تحقيقه.

مبدأ العمل

لا أعرف اللغة الإنجليزية جيدًا ، لذلك من بين العديد من المقالات التي قرأتها حول موضوع أشجار البادئة ، ربما لم تصلني بعض المعلومات. لذلك ، توصلت إلى كيفية ترتيب كل شيء ، وفهم فقط المبدأ الأساسي لشجرة البادئة. بالنسبة لأولئك الذين لا يعرفون ، سأحاول وصفها بشكل أكثر وضوحًا مما هو مكتوب على ويكيبيديا. لذلك شرحت ما كنت أفعله لزوجتي.

شجرة البادئة هي بنية منطقية لتخزين البيانات التي يمكن تمثيلها كمؤشر لبطاقات الكتب في مكتبة. يحتوي كل صندوق على رقم. كل مربع يتوافق مع حرف معين من الأبجدية. يوجد في الداخل أرقام الأدراج التالية ، التي يمكن فتحها لمعرفة ما يلي وما إلى ذلك. عندما لا يوجد شيء داخل الصندوق ، هذا يعني أن حرف هذا المربع هو الأخير في الكلمة. تكمن المشكلة في أن بعض المربعات تظل فارغة تقريبًا ، لأنها تحتوي على رقم أو رقمين ، والمساحة المتبقية فارغة.

لحل هذه المشكلة ، ظهرت العديد من أنواع أشجار البادئة ، بما في ذلك: HAT-trie ، double-array trie ، tripple-array trie. كانت حقيقة أنني لم أستطع أن أفهم تمامًا مبدأ عملهم الذي دفعني إلى شجرة بسيطة مثل ملف بطاقة المكتبة.

تمكنت في المرة الأخيرة من تنفيذ تطبيق استهلاك ذاكرة اقتصادي إلى حد ما لشجرة بادئة بسيطة. بمتابعة هذا الاستعارة بفهرس بطاقة مكتبة ، قمت بعمل أدراج في خزانة الملفات الخاصة بي بأحجام مختلفة ، حيث أن الأبجدية الكاملة يكون الصندوق هو الأكبر ، ولحرف واحد أصغر.

تمكنت من تنفيذ نفس مخطط PHP بالضبط في C.

1. يتم ترميز كل حرف من الكلمات وفقًا للجدول المحدد برقم من 2 إلى 95. على سبيل المثال ، يتم ترميز كلمة "abv" بثلاثة أرقام: 11 ، 12 ، 13. للحصول على أقصى أداء ، يتم استخدام صفيف ثنائي الأبعاد من الأرقام 1 بايت uint8_t abc[256][256] = {}; لتحويل برنامج ، يقرأ سطرًا ببايت واحد ، ويحاول أخذ قيمة كل بايت في صفيفنا. على سبيل المثال ، رمز الرقم هو 1 = 49 ، لذا فإننا ننظر إلى abc[49][0]; . إذا كانت هناك قيمة غير "\ 0" ، فهذا هو رمز رسالتنا ، وتذكرها وانتقل إلى البايت التالي. في حالتنا ، تتكون كلمة "abv" من تسلسل 6 بايت ، وحدتي بايت لكل حرف: 208 ، 176 ، 208 ، 177 ، 208 ، 178. نظرًا لأن ترميز utf-8 مصمم بحيث لا تتزامن البايت الأولى من الأحرف أحادية البايت مع وحدات البايت الأولى متعددة البايت ، في مجموعتنا abc[208][0] = 0; .

ومع ذلك ، بالنسبة لأزواج البايت ، توجد بعض المطابقات:

 /*  [11] */ abc[208][176] = 11; /*  [12] */ abc[208][177] = 12; /*  [13] */ abc[208][178] = 13; 

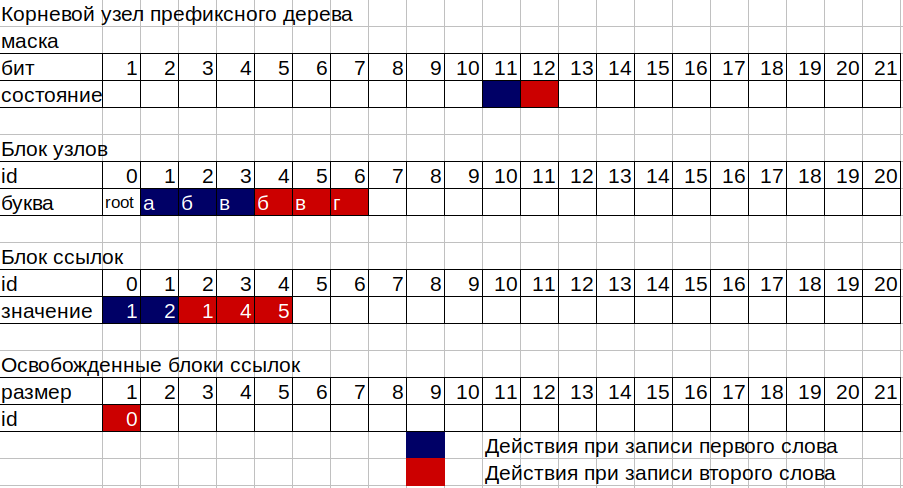
2. الآن نحتاج إلى كتابة الأرقام 11 و 12 و 13 في مربعات شجرتنا. تتكون الشجرة من كتلتين منفصلتين للذاكرة غير المتفجرة ، الأولى عبارة عن كتلة من العقد ، والثانية عبارة عن كتلة من الروابط ، بالإضافة إلى عددين من العقد المشغولة وخلايا مشغولة لكتلة من الروابط. تتكون كل عقدة شجرة من 16 بايت و 12 بايت من قناع البت و 4 بايت لتخزين معرف كتلة الارتباط. يسمح لك القناع بتخزين الأرقام من 2 إلى 96 بت. يتم استخدام البت الأول من القناع لوضع علامة على نهاية الكلمة على هذه العقدة. يمكن أن تتوافق كل عقدة مع المعرف من كتلة الارتباط إذا تمت كتابة حرف واحد على الأقل في هذه العقدة ، أو لا تتطابق إذا كانت العقدة "ورقة" من حيث الأشجار ، أي أن الكلمة تنتهي ببساطة. يعبر عنه في مكتبة ، درج فارغ.

3. خذ قناع العقدة الأولى (الجذر). trie-> nodes [0] .mask؛ نحسب البتات المرفوعة في هذا القناع ، بدءًا من الثانية (الأولى لكلمة نهاية الكلمة). إذا لم يتم رفع أي بت في القناع ، أي نظرًا لأن العقدة فارغة ، فإننا نحتاج إلى كتلة ارتباط من الحجم 1 لتخزين رقمنا 11 ، وأخذ الرقم من عداد ارتباط الارتباط الخاص بالكتلة وقم بزيادة القيمة القديمة بمقدار واحد (لأننا بحاجة إلى الحجم 1). نأخذ الرقم من عداد العقدة ونزيد أيضًا القيمة القديمة بمقدار 1. نكتب في عقدة الجذر لدينا معرف كتلة الارتباط ، وهو الرقم الذي تم الحصول عليه من عداد كتلة الارتباط. وفي هذا المعرف لكتلة الارتباط ، اكتب معرف العقدة الجديدة ، أي الرقم الذي تم الحصول عليه من عداد العقدة. الآن ، بالإضافة إلى العقدة الجذرية (id 0) ، لدينا عقدة من الحرف "a" (id 1). لكتابة الرقم 12 المقابل للحرف "b" ، نفعل نفس الشيء ، ولكن مع عقدة الحرف "a".

4. في الحرف الأخير "c" ، لا نحتاج إلى مكان في كتلة الارتباط ، حيث سيكون لدينا العقدة الأخيرة في الفرع أو العقدة - ورقة. تحتوي هذه العقدة على بت واحد فقط في القناع المرفوع.

5. يحدث الجزء الأصعب من عمل الشجرة عندما تتم كتابته على عقدة تمت فيها كتابة بعض الأحرف بالفعل. في هذه الحالة ، يكون مخطط التشغيل على النحو التالي:

افترض أننا نريد إضافة كلمة "bvg" (12 ، 13 ، 14) إلى شجرتنا ، حيث تم كتابة كلمة "abv" (11 ، 12 ، 13) بالفعل. نحن نحسب البتات في قناع العقدة الجذرية إلى جزء من الرسالة التي تهمنا. لدينا الحرف "b" مع الرمز 12 ، مما يعني أن بت هذا الحرف هو 12 ، في القناع من 1 إلى 12 بتة 11 من الحرف "a" تم رفعه بالفعل. لذلك لدينا الحجم الحالي لكتلة الارتباط للعقدة الجذرية 1. نكتب الحرف الثاني ، لذلك نحن بحاجة الآن إلى كتلة ارتباط بحجم 2. هنا يبدأ تشغيل كتل القطع المحررة ، حيث لم يعد يتم استخدام معرف وحجم الأقسام في كتلة الارتباط بواسطة العقد شجرة. معرفنا القديم لكتلة الارتباط للعقدة الجذرية من الحجم 1 يدخل فقط في تسجيل الأقسام المجانية من الحجم 1 ، لأن عقدة الجذر لدينا تحتاج إلى حجم أكبر. لا يحتوي التسجيل الخاص بنا على قسم مناسب من الحجم 2 ونأخذ مرة أخرى القيمة من عداد كتلة الارتباط كمعرف جديد لكتلة الارتباط ، وزيادة العداد بمقدار 2. في العنوان الجديد لكتلة الارتباط بنفس الترتيب الذي توجد فيه البتات في قناع العقدة ، نكتب قيمة الهوية عقدة من كتلة الروابط القديمة للحرف "أ" للكلمة الأولى وقيمة العقدة التي تم إنشاؤها للتو للحرف "ب" من الكلمة الثانية.

سرعة العمل

يبدو طبل لفة ... أتذكر النتيجة الأخيرة؟ حوالي 80 ألف كلمة في الثانية. تم إنشاء الشجرة من قاموس جميع الكلمات الروسية OpenCorpora 3 039 982 كلمة. وإليك ما حدث الآن:

 yatrie creation time: 4.588216s (666k wps) yatrie search time 1 mln. rounds: 0.565618s (1.76m wps) 

تحديث 11/01/2018:
في الإصدار 0.0.2 ، كان من الممكن زيادة السرعة مرتين تقريبًا عن طريق استبدال الوظائف الكاملة بوظائف الماكرو ، بالإضافة إلى تغيير بنية قناع العقدة إلى uint32_t mask [3] ، وكان سابقًا uint8_t mask [12].
تمت أيضًا إضافة وحدات الماكرو LIKELY () UNLIKELY () للتنبؤ بالنتائج المتوقعة في تلك الكتل إذا كانت () ، حيثما أمكن.
تحديث 11/05/2018:
الملتوية أكثر قليلاً. تمكنت من جعلها تعمل بشكل جيد حتى عند تجميع -O3 و -Ofast. سرعة البحث في الشجرة هي 0.2 μs أو 0.2c لكل مليون تكرار. على ما يبدو تم الحصول على هذه السرعة بسبب الانتقال إلى تنسيق مختلف للقناع. في السابق ، كان هناك 12 بايت من 8 بت ، والآن 3 int32 ووظيفة سريعة جدًا لحساب البت في int32.

ما مدى ضغط هذا؟

يحتاج قاموس OpenCorpora المحدد إلى 84 ميغابايت تقريبًا ، وهو ليس أسوأ بكثير من libdatrie الذي يعطي ~ 80 ميغابايت.

→ كود المصدر

مرحبًا