هذا هو البرنامج التعليمي مكتبة TensorFlow. اعتبرها أعمق قليلاً من المقالات حول التعرف على الأرقام المكتوبة بخط اليد. هذا هو البرنامج التعليمي حول طرق التحسين. هنا لا يمكنك الاستغناء عن الرياضيات. لا بأس إذا نسيت ذلك تمامًا. أذكر. لن يكون هناك دليل رسمي واستنتاجات معقدة ، فقط الحد الأدنى الضروري للفهم الحدسي. بادئ ذي بدء ، خلفية صغيرة حول كيف يمكن أن تكون هذه الخوارزمية مفيدة في تحسين الشبكة العصبية.

قبل ستة أشهر ، طلب مني أحد الأصدقاء أن أبين كيفية إنشاء شبكة عصبية في Python. تنتج شركته أدوات للقياسات الجيوفيزيائية. تقوم عدة مجسات مختلفة أثناء الحفر بقياس مجموعة من الإشارات المرتبطة بمعلمات البيئة المحيطة بالبئر. في بعض الحالات المعقدة ، احسب بدقة المعلمات البيئية من الإشارات لفترة طويلة حتى على جهاز كمبيوتر قوي ، ومن الضروري تفسير نتائج القياس في هذا المجال. كانت هناك فكرة لإحصاء عدة مئات الآلاف من الحالات على كتلة ، وتدريب شبكة عصبية عليها. نظرًا لأن الشبكة العصبية سريعة جدًا ، يمكن استخدامها لتحديد المعلمات التي تتوافق مع الإشارات المقاسة ، مباشرة في عملية الحفر. التفاصيل في المقالة:
Kushnir ، D. ، Velker ، N. ، Bondarenko ، A. ، Dyatlov ، G. ، & Dashevsky ، Y. (2018 ، 29 أكتوبر). محاكاة في الوقت الحقيقي لأداة المقاومة السمتية العميقة في نموذج العطل الثنائي الأبعاد باستخدام الشبكات العصبية (الروسية). جمعية مهندسي البترول. دوى: 10.2118 / 192573-RU
في إحدى الليالي ، أوضحت كيف يمكن لـ Keras تنفيذ شبكة عصبية بسيطة ، وبدأ صديق في العمل في التدريب على البيانات المحسوبة. بعد يومين ، ناقشنا النتيجة. من وجهة نظري ، بدا واعدًا ، لكن أحد الأصدقاء قال إنه بحاجة إلى حسابات بدقة الجهاز. وإذا تبين أن الخطأ التربيعي المتوسط هو حوالي 1 ، عندئذ تكون هناك حاجة إلى 1e-3. 3 أوامر أقل. ألف مرة.
لم تسفر التجارب على بنية الشبكة العصبية ، وتطبيع البيانات ، ونهج التحسين عن شيء تقريبًا. بعد أسبوعين ، اتصل أحد الأصدقاء وقال إنه قام بتثبيت MatLab وحل المشكلة بطريقة Levenberg-Marquardt (فيما يلي سوف نطلق عليها LM ). تم تحسينه لفترة طويلة (عدة أيام) ، ولم يعمل على GPU ، ولكن النتيجة كانت صحيحة. بدا الأمر وكأنه تحد.
فشل البحث السريع عن مُحسّن LM جاهز لـ keras أو TensorFlow. لم أجد مكتبة البيرن إلا أن وظائفها بدت لي فقيرة. قررت تنفيذ ذلك بنفسي. للوهلة الأولى ، بدا كل شيء بسيطًا ، وكان يجب أن تكون أمسيتان كافيتين. استغرق الأمر وقتًا أطول. كانت هناك مشكلتان:
- TensorFlow. مجموعة من المقالات ، ولكن جميع المستويات تقريبًا "ولكن دعنا نكتب
مرحباً بالتعرف على الأرقام المكتوبة بخط اليد". - الرياضيات لقد نسيت الكثير ، ولا يهتم مؤلفو المقالات الرياضية بأشخاص مثلي على الإطلاق: صيغ صلبة بدون تفسير ، "من الواضح!" وهكذا دواليك.
نتيجة لذلك ، كتب مقالًا لأولئك الذين نسوا الرياضيات ويريدون فهم TensorFlow بشكل أعمق قليلاً ، ولكن بدون المتشددين. تحتوي المقالة على الكثير من النصوص ورمز قليل. الخيار المعاكس ، عندما يكون هناك نص قليل والكثير من التعليمات البرمجية ، هنا Jupyter Notebook Levenberg-Marquardt .
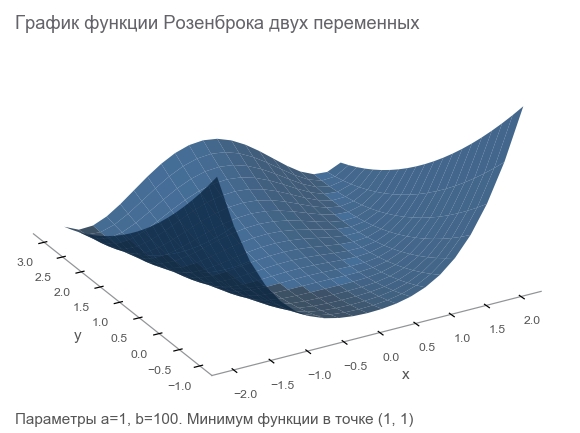
تعرف على ميزة Rosenbrock
سننشئ بيانات التدريب بواسطة وظيفة Rosenbrock ، والتي تُستخدم غالبًا كمعيار لخوارزميات التحسين:
f ( x ، y ) = ( a - x ) 2 + b ( y - x 2 ) 2
لماذا هي جيدة؟
- جدول جميل. يطلق عليه وادي Rosenbrock ووظيفة الموز غير القابلة للترجمة في Rosenbrock .
- الحد الأدنى العالمي هو داخل واد مستوي مكافئ طويل وضيق. العثور على واد أمر تافه ، والحد الأدنى العالمي صعب.
- هناك خيار متعدد الأبعاد. ليس من السهل ابتكار وظيفة جيدة للعديد من المتغيرات.
سنبدأ في كتابة التعليمات البرمجية منه عن طريق ربط المكتبات اللازمة لمزيد من العمل:
import numpy as np import tensorflow as tf import math def rosenbrock(x, y, a, b): return (a - x)**2 + b*(y - x**2)**2
نذكر المشكلة
نظرًا لأننا كنا نتحدث عن جهاز قياس ، فلنستمر في استخدام القياس. يمكن لجهازنا في عالم خيالي قياس الإحداثيات ( س ، ص ) والطول ض . درس الفيزيائيون العالم وقالوا: " نعم ، هذا هو روزنبروك! معرفة الإحداثيات ، يمكنك حساب الارتفاع بدقة ، لا تحتاج إلى قياسه ". وبعبارة أخرى ، قدم لنا العلماء نموذجًا z = r o s e n b r o c k ( x ، y ، a ، b ) الذي يعتمد على المعلمات ( أ ، ب ) . هذه المعلمات ، على الرغم من أنها ثابتة في عالم خيالي ، غير معروفة. يجب العثور عليهم.
أجرينا سلسلة من التجارب التي أعطت م النقاط (x1،y1،z1)،(x2،y2،z2)،...،(xm،ym،zm) :
الطريقة الأولى للتحسين هي محاولة تخمين المعلمات. نستخدم مكتبة Numpy:
x, y = data_points[:, 0], data_points[:, 1] z = data_points[:, 2]
كيف نفهم كم نحن مخطئون؟ عد البقايا - أحجام الخطأ. م تعطي النقاط م بقايا - تحتاج إلى مؤشر متكامل. نقوم بتربيع كل متبق في مربع ونحسب المتوسط:
MSE(a،b)= frac1m summi=1(zi− widehatzi)2
يسمى هذا المقرب متوسط الخطأ التربيعي (المشار إليه فيما يلي بـ mse ):
[Out]: 3868.2291666666665
من خلال تقليل mse ، نحل مشكلة المربعات الصغرى ( تصغير المربعات غير الخطية ):
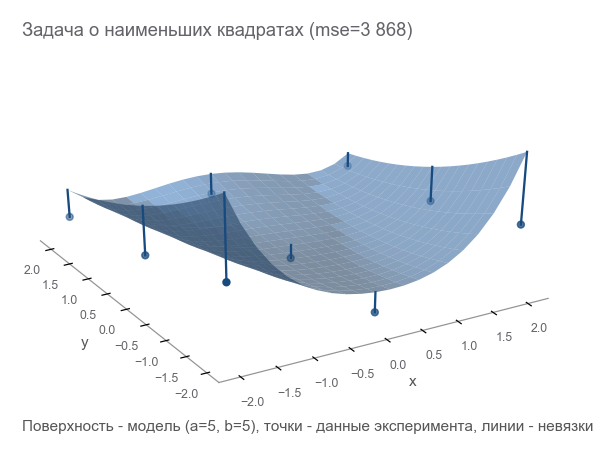
يمكن ملاحظة أن المعلمات لم تخمن على الإطلاق.
نقوم بصياغة المشكلة على TensorFlow
النموذج لديه الشكل z=rosenbrock(x،y،a،b) . نأتي إلى النموذج y=f(x،p) (عادة ما تكتب الرياضيات بيتا بدلا من p لكن المبرمجين لا يستخدمون بيتا). الآن النموذج لديه الشكل y=rosenbrock(x،p) أين y - الارتفاع x هو ناقل الإحداثيات لعنصرين (مكون) ، و p - متجه المعلمات.
غالبًا ما يفكر المبرمجون في المتجهات باعتبارها مصفوفات أحادية البعد. هذا ليس صحيحًا تمامًا. مجموعة من الأرقام هي وسيلة لتمثيل المتجه. يمكنك تمثيل متجه كمصفوفة من البعد N ، صفيف ثنائي الأبعاد 1 مراتN ، وحتى مصفوفة N ضرب1 في الحالات التي تكون فيها حقيقة أن المتجه متجه عمود (على سبيل المثال ، ضرب المصفوفة به) مهم:
startbmatrixx1 vdotsxN endbmatrix
يستخدم TensorFlow مفهوم الموتر . يمكن أن يكون الموتر ، مثل المصفوفة ، أحادي البعد (لتمثيل متجه ) ، ثنائي الأبعاد ( لمصفوفة أو متجه عمود ) وأي بُعد أكبر.
لا يختلف رمز TensorFlow في رمز Numpy. المحتوى ضخم. يحسب رمز Numpy قيمة mse. لا يقوم كود TensorFlow بإجراء أي حسابات على الإطلاق ، فهو يشكل رسمًا بيانيًا لتدفق البيانات يمكن أن تحسبه mse. إن اللحظة التي تتحمل الدماغ هي عمل وظيفة روزنبروك . نستخدمها في كلتا الحالتين. ولكن عند تمرير المصفوفات Numpy ، فإنها تقوم بإجراء الحسابات وفقًا للصيغة وإرجاع الأرقام. وعندما ننقل الموتر إلى TensorFlow ، فإنه يشكل رسمًا فرعيًا لدفق البيانات ويعيد حافته في شكل موتر. معجزات تعدد الأشكال ، ولكن لا تسيء استخدامها:
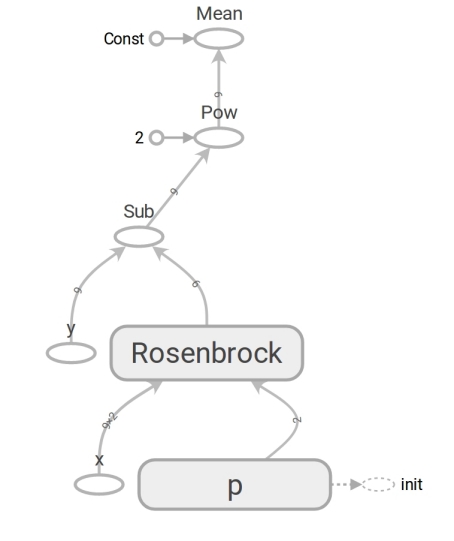
بفضل وجود رسم بياني لتدفق البيانات ، فإن TensorFlow على وجه الخصوص قادر على حساب المشتقات تلقائيًا (باستخدام تقنية التمايز التلقائي في الوضع العكسي ).
لحظة رياضيات. سيتم إخفاء كتل "لأولئك الذين نسيوا" في المفسد.
مشتق (العدد المدخل - العدد المتبقي)الأرجح أنك تتذكر تعريف مشتق دالة العددية (إرجاع رقم) لمتغير واحد: for f: mathbbR rightarrow mathbbR مشتق f عند هذه النقطة x in mathbbR يعرف بأنه:
f′(x)= limh to0 fracf(x+h)−f(x)h
المشتقات هي طريقة لقياس التغيير . في الحالة العددية ، يوضح المشتق مقدار تغير الوظيفة f إذا x التغيير إلى قيمة صغيرة varepsilon :
f(x+ varepsilon) تقريباf(x)+ varepsilonf′(x)
للراحة ، نشير إلى y=f(x) والمشتق y بواسطة x سنكتب كيف frac جزئيy جزئيx . مثل هذا السجل يؤكد ذلك frac جزئيy جزئيx - معدل التغيير بين المتغيرات x و y . وبشكل أكثر تحديدًا ، إذا x التغيير إلى varepsilon ثم y التغيير إلى تقريبا varepsilon frac جزئيy جزئيx . يمكنك أيضًا كتابتها على النحو التالي:
x rightarrowx+ Deltax Rightarrowy rightarrow almosty+ frac جزئيy جزئيx Deltax
يقرأ على النحو التالي: "متغير x على x+ Deltax التغيير y تقريبا y+ Deltax frac جزئيy جزئيx هذا السجل يبرز بوضوح العلاقة بين التغيير x والتغيير y .
أنشأنا رسمًا بيانيًا لتدفق البيانات ، فلنجرِ حساب mse:
[Out]: 3868.2291666666665
والنتيجة هي نفسها مع Numpy. لذلك لم يخطئوا.
ابدأ التحسين
لسوء الحظ ، لم يكن من الممكن تخمين المعلمات. ولكن بعد ذلك:
- قمنا بتعيين معيار المثالية - الحد الأدنى لقيمة mse.
- تم تحديد المعلمات المتغيرة: متجه p مع المكونات a ، b وظائف روزنبروك.
- لم نفكر في القيود بعد ، لكنها ليست هناك.
في الخطوة الأخيرة ، قمنا ببناء رسم بياني لتدفق البيانات مع موتر خسارة محدودة ( وظيفة الخسارة ). الهدف من التحسين هو العثور على قيمة متجه المعلمة p حيث تكون قيمة دالة الخسارة عند الحد الأدنى. كنا محظوظين ، الرسم البياني لهذه الوظيفة بسيط للغاية (مقعر وبدون حد أدنى محلي):
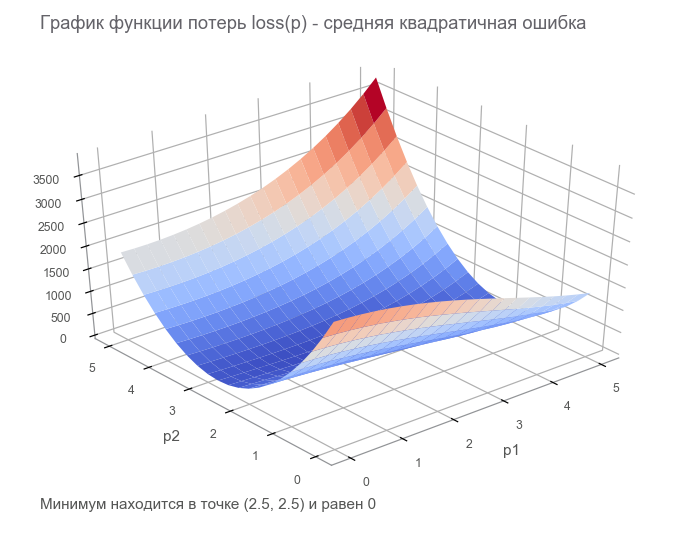
الشروع في التحسين. للبدء ، نكتب دورة معممة:
نحسن بطريقة أسرع نزول التدرج (SGD)
يمكن مقارنة أفعال هذه الطريقة بركوب متزلج جريء ، والذي يضع دائمًا المنحدر (في الاتجاه الأكثر حدة). في هذه الحالة ، يتم فقط مراعاة المنحدر عند نقطة الموقع. وإذا كان المنحدر قويًا ، فإن المتزلج يطير مسافة طويلة قبل التغيير التالي. مع منحدر ضعيف ، يتحرك في خطوات صغيرة. ربما كيف تطير بعيدا إلى شجرة ( تختلف الخوارزمية ) ، وتتعثر في حفرة ( الحد الأدنى المحلي ).

يمكنك الكتابة على النحو التالي (التغيير boldsymbolp على boldsymbolp−... ):
boldsymbolp rightarrow boldsymbolp− alpha[ nablapالخسارة( boldsymbolp)]
دهني boldsymbolp يؤكد أن هذه هي نقطة الموقع الفعلي - قيمة متجه المعلمة في الخطوة الحالية. في الخطوة الأولى ، هذا هو تخميننا (5 ، 5). هناك نقطتان مثيرتان للاهتمام في الصيغة: alpha - معدل التعلم ( معدل التعلم ) ، nablapخسارة - التدرج ( التدرج ) لدالة الخسارة بمتجه المعلمات.
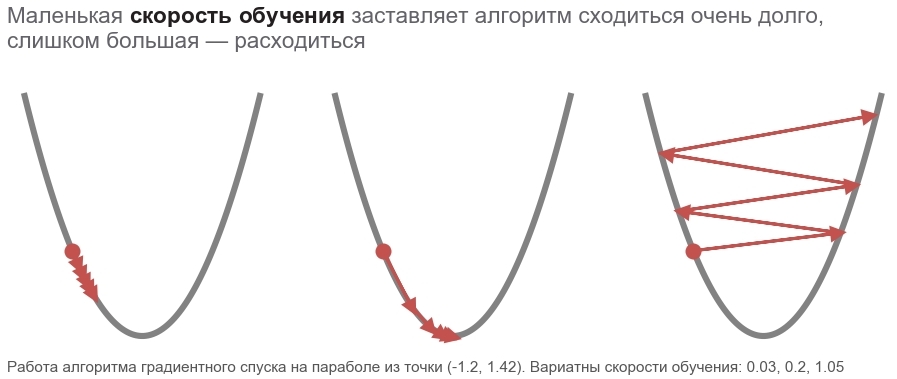
التدرج (تم إدخال المتجه - عدد اليسار)ضع في اعتبارك دالة تأخذ المتجه كمدخل وتنتج عدديًا: f: mathbbRN rightarrow mathbbR . مشتق f عند هذه النقطة x in mathbbRN يسمى الآن التدرج وهو ناقل [ nablaxf(x)] in mathbbRN (تُقرأ باسم "نبلة") وتتكون من مشتقات جزئية :
nablaxy=( frac جزئيy جزئيx1، frac جزئيy جزئيx2،...، frac جزئيy جزئيxN)
في هذه الحالة ، يكون سجل اعتماد تغيير الوظيفة على تغيير الوسيطة كما يلي:
x rightarrowx+ Deltax Rightarrowy rightarrow almosty+ nablaxy cdot Deltax
لقد تغير السجل قليلاً جدًا لأخذ ذلك في الاعتبار x ، Deltax و nablaxy - ناقلات في mathbbRN و y - العددية. عند مضاعفة المتجهات nablaxy و Deltax يتم استخدام منتج العددية (مجموع منتجات المكونات).
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 1381.5379689135807 [...] ENDED ON STEP: 582, FINAL LOSS: 9.698531012270816e-11 PARAMETERS: [2.50000205 2.49999959]
استغرق 582 خطوة:
الحركة في اتجاه مضاد للتدرجلماذا نتحرك في الاتجاه المعاكس للتدرج؟ أذكر الإدخال بمنتج العددية: x rightarrowx+ Deltax Rightarrowy rightarrow almosty+ nablaxy cdot Deltax . التقليل y . نظرًا لأن سلوك الوظيفة لا يُعرف إلا في حي صغير من خلال المشتق ، فمن الضروري التحرك في خطوات صغيرة ، ولكن المثلى ، وتقليل المنتج nablaxy cdot Deltax . وفقًا لتعريف المدرسة ، يكون الناتج القياسي لمتجهين هو العدد الذي يساوي ناتج أطوال هذه المتجهات بواسطة جيب الزاوية بينهما : a cdotb= left|a right| left|b right|cos angle(a،b) . للحصول على طول ثابت للمتجهات ، يصل هذا المنتج إلى الحد الأدنى مع جيب تمام -1 ، أي بزاوية 180 درجة ، عندما يتم توجيه المتجهات في اتجاهين متعاكسين. وفقا لذلك ، الحد الأدنى من المنتجات العددية nablaxy cdot Deltax يتحقق عندما Deltax في اتجاه مضاد للتدرج .
نحسن بطريقة آدم
لن نذهب أبعد من ذلك في طرق التدرج ، ولكن هناك العديد من الاختلافات. يمكنك أن تقرأ عنها في المقالة طرق تحسين الشبكات العصبية . في TensorFlow ، تم تنفيذ العديد من المُحسنات بالفعل. على سبيل المثال ، آدم:
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 34205.72916492336 [...] ENDED ON STEP: 317, FINAL LOSS: 2.424142714263483e-12 PARAMETERS: [2.49999969 2.50000008]
تمكنت في 317 خطوة. أسرع بكثير.
نقوم بتحسين طريقة نيوتن
يمكن مقارنة إجراءات طرق الدرجة الثانية بركوب لوح التزلج الحر العقلاني الذي يفكر في النقطة التالية من طريقه لفترة طويلة ويأخذ في الاعتبار ليس فقط المنحدر في الموقع ، ولكن أيضًا الانحناء.
في الواقع ، تحاول كل من طرق نزول التدرج وطرق الدرجة الثانية تخمين ( تقريبًا ) الوظيفة عند النقطة الحالية. تركز طرق التدرج فقط على منحدر الرسم البياني للدالة عند النقطة - المشتق الأول. طرق الدرجة الثانية ، بالإضافة إلى التحيز ، تأخذ في الاعتبار الانحناء ، المشتق الثاني: "إذا استمر الانحناء ، فأين سيكون الحد الأدنى؟" نحسب ونذهب إلى هناك:
لإنشاء مثل هذا التقريب وحساب الحد الأدنى للنقطة المقدرة ، يمكنك استخدام سلسلة Taylor . بالنسبة للحالة أحادية البعد ، التقريب بواسطة متعدد الحدود من الدرجة الثانية عند النقطة a يبدو مثل هذا:
f(x) almostf(a)+ fracf′(a)(x−a)1!+ fracf″(a)(x−a)22!
تم الوصول إلى الحد الأدنى في x=a− fracf′(a)f″(a) . تبدو الحالة متعددة الأبعاد أكثر خطورة:
مصفوفة هسه (دخل متجه - عدد اليسار)المصفوفة Hessian هي مصفوفة مربعة تتكون من مشتقات ثانية:
\ boldsymbol {H} y_ {x} = \ start {bmatrix} \ frac {\ جزئي ^ 2y} {\ جزئي x_1 ^ 2} & \ frac {\ جزئي ^ 2y} {\ جزئي x_1 \ جزئي x_2} & \ cdots & \ frac {\ جزئي ^ 2y} {\ جزئي x_1 \ جزئي x_N} \\ \ frac {\ جزئي ^ 2y} {\ جزئي x_2 \ جزئي x_1} و \ frac {\ جزئي ^ 2y} {\ جزئي x_2 ^ 2} & \ cdots & \ frac {\ جزئي ^ 2y} {\ جزئي x_2 \ جزئي x_N} \\ \ vdots و \ vdots & \ ddots & \ vdots \\ \ frac {\ جزئي ^ 2y} {\ جزئي x_N \ جزئي x_1} & \ frac {\ جزئي ^ 2y} {\ جزئي x_N \ جزئي x_2} & \ cdots & \ frac {\ جزئي ^ 2y} {\ جزئي x_N ^ 2} \ end {bmatrix}
تقريب كثير الحدود من الدرجة الثانية لوظيفة ناقل من خلال التدرج ومصفوفة Hessian عند نقطة a يبدو مثل هذا:
f(x) almostf(a)+(xa) intercal[ nablaxf(a)]+ frac12!(xa) intercal[ boldsymbolHfx(a)](xa)
تم الوصول إلى الحد الأدنى في x=a−[ boldsymbolHfx(a)]−1[ nablaxf(a)] . يتطابق الشكل عمليًا مع الحالة أحادية البعد: استبدلنا المشتق الأول بتدرج ، والثاني بمصفوفة Hessian وقمنا بتصحيح للعمل مع المتجهات. من المستحيل تقسيم المتجه بواسطة مصفوفة ، لذلك يتم استخدام الضرب في المصفوفة العكسية . T تعني تبديل . تشير الصيغة إلى أن المتجه بشكل افتراضي هو عمود. تبديل يحول متجه العمود إلى متجه صف . عند التنفيذ على TensorFlow ، يجب أن يؤخذ هذا في الاعتبار ، ولكن في الاتجاه المعاكس: بشكل افتراضي ، يكون المتجه عبارة عن سلسلة (موتر أحادي البعد). فقط في حالة: التبديل ليس دورانًا بمقدار 90 درجة ، إنه تحويل الصفوف إلى أعمدة بنفس الترتيب.
لذا ، فإن خطوة طريقة نيوتن لها الشكل التالي:
boldsymbolp rightarrow boldsymbolp−[ boldsymbolHlossp( boldsymbolp)]−1[ nablapخسارة( boldsymbolp)]
يحتوي TensorFlow على كل شيء لتطبيق هذه الطريقة:
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 105.04357496954218 step: 4, current loss: 9.96663526704236 ENDED ON STEP: 6, FINAL LOSS: 5.882202372519996e-20 PARAMETERS: [2.5 2.5]
يكفي 6 خطوات:
الأمثل من قبل خوارزمية غاوس-نيوتن
طريقة نيوتن لها عيب واحد - مصفوفة هيسن. بفضل TensorFlow ، يمكننا حسابه في سطر واحد من التعليمات البرمجية. وفقًا لويكي ، ذكر يوهان كارل فريدريش جاوس أول أسلوب له في عام 1809. حساب المصفوفة Hessian لعدة معلمات لأسلوب المربعات الصغرى يمكن أن يستغرق الكثير من الوقت. يمكننا الآن أن نفترض أن خوارزمية Gauss-Newton تستخدم تقريب مصفوفة Hessian من خلال مصفوفة Jacobi لتبسيط الحسابات. ولكن من وجهة نظر التاريخ ، فإن الأمر ليس كذلك: ولد لودفيج أوتو هيس (الذي طور المصفوفة التي سميت باسمه) في عام 1811 - بعد عامين من أول ذكر للخوارزمية. وكان كارل جوستاف جاكوبي في الخامسة من عمره.
لا تعمل خوارزمية Gauss-Newton مع وظيفة الخسارة. يعمل مع الوظيفة المتبقية r(p) . تأخذ هذه الوظيفة متجه إدخال المعلمات p ويعيد متجه المتبقية . في حالتنا ، المتجه p يتكون من مكونين (معلمات a و b وظائف Rosenbrock) والمتجه المتبقي من م مكون (حسب عدد التجارب). يتم الحصول على دالة المتجه لوسيطة المتجه. مشتقها:
مصفوفة جاكوبي (تم إدخال المتجه - تم إصدار المتجه)ضع في اعتبارك وظيفة تأخذ المتجه كمدخل وتنتج متجهًا أيضًا: f: mathbbRN rightarrow mathbbRM . مشتق f عند هذه النقطة x الآن لديه حجم N ضربM تسمى مصفوفة جاكوبي ، وتتكون من جميع مجموعات المشتقات الجزئية:
\ boldsymbol {J} y_ {x} = \ start {pmatrix} \ frac {\ جزئي y_ {1}} {\ جزئي x_ {1}} & \ cdots & \ frac {\ جزئي y_ {1}} {\ جزئي x_ {N}} \\ \ vdots & \ ddots & \ vdots \\ \ frac {\ جزئي y_ {M}} {\ جزئي x_ {1}} & \ cdots & \ frac {\ جزئي y_ {M}} {\ جزئي x_ {N}} \ end {pmatrix}
قد تلاحظ أن صفوف مصفوفة Jacobi هي تدرجات المكونات y . البند (i،j) المصفوفات frac جزئيy جزئيx يساوي frac جزئيyi جزئيxj ويخبرنا كم سيتغير yi عند التغيير xj على قيمة صغيرة. كما في الحالات السابقة ، يمكنك كتابة:
x rightarrowx+ Deltax Rightarrowy rightarrow almosty+ boldsymbolJyx Deltax
هنا boldsymbolJyx مصفوفة N ضربM و Deltax ناقلات الحجم N وبالتالي المنتج boldsymbolJyx Deltax هو نتاج المصفوفة بواسطة المتجه ، مما ينتج عنه ناقل الحجم M .
من أجل عدم الخلط في وفرة الشخصيات ، نفترض ذلك boldsymbolJr - مصفوفة جاكوبي للوظائف المتبقية عند النقطة الحالية boldsymbolp . ثم يمكن كتابة خوارزمية Gauss-Newton على النحو التالي:
boldsymbolp rightarrow boldsymbolp−[ boldsymbolJ rintercal boldsymbolJr]−1 boldsymbolJ rintercalr( boldsymbolp)
يتزامن التسجيل في النموذج تمامًا مع تسجيل طريقة نيوتن. فقط بدلاً من استخدام مصفوفة Hessian boldsymbolJ rintercal boldsymbolJr بدلاً من التدرج boldsymbolJ rintercalr( boldsymbolp) . بعد ذلك ، سنرى لماذا يمكن استخدام هذا التقريب. في هذه الأثناء ، دعنا ننتقل إلى التنفيذ على TensorFlow:
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 14.653025157673625 step: 4, current loss: 4.3918079172783016e-07 ENDED ON STEP: 4, FINAL LOSS: 3.374364957618591e-17 PARAMETERS: [2.5 2.5]
يكفي 4 خطوات. أقل من طريقة نيوتن.
كما يتبين من الكود ، لا يتم استخدام وظيفة الخسارة في التحسين ، فقط لمعايير التوقف والتسجيل. كيف تعرف خوارزمية التحسين أي وظيفة يجب تقليلها؟ الجواب مدهش: مستحيل! يقلل غاوس نيوتن فقط من الخطأ التربيعي .
إصلاح الجزء الرياضي من المقالة
كررنا كل الرياضيات التي احتجناها. دعنا نصلحها قليلاً من أجل زيادة التركيز فقط على البرمجة و TensorFlow. قد تحتاج إلى قلم رصاص لتتبع تسلسل الإجراءات الرياضية.
هناك نموذج y=f(x،p) أين x - ناقلات p - متجه معلمات البعد n و y - العددية. من التجارب الواردة م النقاط (x1،y1)،...،(xm،ym) ( أزواج البيانات ). تعتمد الوظيفة المتبقية للمتجه فقط على متجه المعلمة: r(p)=(r1(p)،...rm(p)) أين rk(p)=yk− widehatyk=yk−f(xk،p) . , p , xk,yk ؟؟؟ , xk,yk , .
p , ( sum of squared error — sse residual sum-of-squares — rss ) . mse sse , م . . :
loss(p)=r21(p)+⋯+r2m(p)=m∑k=1r2k(p)
p (p) .
, . — . — , r2 2r∂r∂p . :
∇ploss=(m∑k=12rk∂rk∂p1,⋯,m∑k=12rk∂rk∂pn)
. :
[Hlossp]ij=∂2loss∂pi∂pj=m∑k=1(2∂rk∂pi∂rk∂pj+2rk∂2rk∂pi∂pj)
. , , (uv)′=u′v+uv′ .
عظيم! .
, , , — 2rk∂2rk∂pi∂pj . , , rk , . — . , ? -.
:
Jr=(∂r1∂p1⋯∂r1∂pn⋮⋱⋮∂rm∂p1⋯∂pm∂pn)
, , . لاحظ أن:
2Jr⊺
"" . ( ). , — , .
( ):
, , - — , mse .
. , , . , . , .
, : " . - ! ". , , , ( supervised learning ). , . : ( training set ) — ; — ( prediction model ) ; — , .
( multi-layer perceptron neural network mlp ). , , :
- ( starting values ) . Xavier'a, .
- ( overfitting ). — . , . — .
- ( scaling of the input ). , .
9 . 500:
500 . — ( learner ), ( outcome measurement ) ( features ) .
( network diagram ). MatLab:
( input ). ( weights ) 2x10, ( bias ) 10, ( activation ). () ( hidden layer ) 10 . , , ( output ).
, , ( ):
:
. "" , - . 41 . , .
, . - من :
Adam
Adam . mse :
[Out]: step: 1, current loss: 671.4242576535694 [...] ENDED ON STEP: 40000, FINAL LOSS: 0.22862158574440725 VALIDATION LOSS: 0.29000289644978866
. : , , .
2 . :
:
. , 4 . 4 tf.concat .
. tf.while_loop , , , stack .
: . tf.reshape (-1,) .
. - . — TensorFlow . — - - . -. Levenberg-Marquardt Jupyter Notebook rosenbrock_train.py . , TensorFlow . - , ( ) , , .
-
hess_approx grad_approx -. , . :
- :
- :
، ، ، . - , :
، - .
[Out]: step: 1, current loss: 548.8468777701685 step: 2, current loss: 49648941.340197295 InvalidArgumentError: Input is not invertible.
- . , . - , .
, .
-
. Matlab trainlm . . MathWorks.
- : . - :
( ). , -. , . , LM -.
:
mu = tf.placeholder(tf.float64, shape=[1]) n = tf.add_n(parms_sizes) I = tf.eye(n, dtype=tf.float64)
؟؟؟ LM - . , . , , . — , mse . , :
[Out]: step: 1, mu: 3.0 current loss: 692.6211687622557 [...] ENDED ON STEP: 100, FINAL LOSS: 0.012346989371823602 VALIDATION LOSS: 0.01859463694102034
100 LM mse 10 , 40 .
. , . , rosenbrock_train.py .
2D . . . , " " ( curse of dimentionality , Bellman, 1961). . .
:
rosenbrock_train.py get_rand_rosenbrock_points .
-
- : " ! 4 , 300! ". , ( ) -. , , . - . . : ? , . . , - :
- 10 000 6D .
- 3 12, 10, 8 (311 ).
- .
- 3.5 .
. - 2 . LM . 20 .
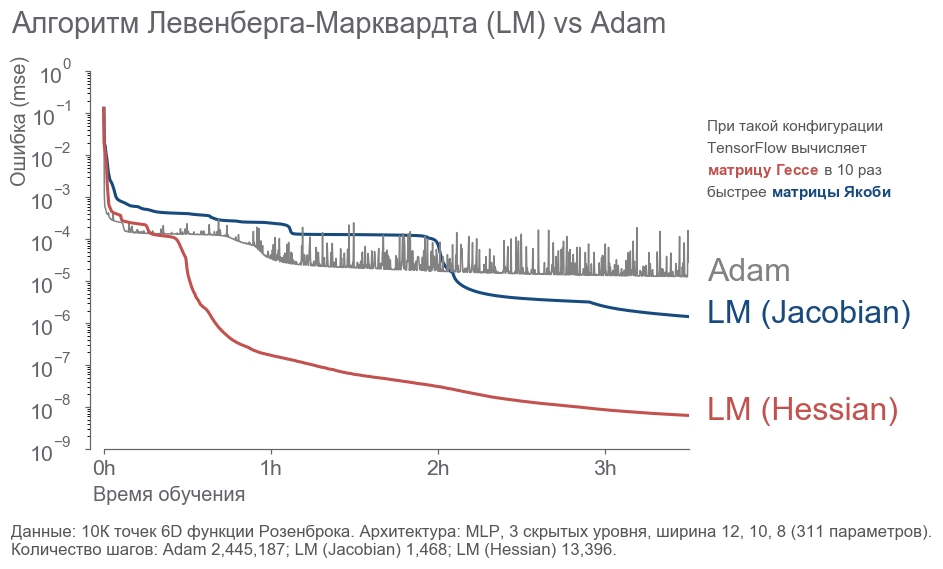
rosenbrock_train.py . . , .
الخلاصة
, . " ", , . , . , 273 . - , .
, :
- .
- ( ) -:
[1] Petros Drineas, Ravi Kannan, and Michael W. Mahoney. 2006. Fast Monte Carlo Algorithms for Matrices I: Approximating Matrix Multiplication. SIAM J. Comput. 36, 1 (July 2006), 132-157. DOI= http://dx.doi.org/10.1137/S0097539704442684
[2] Adelman, M., & Silberstein, M. (2018). Faster Neural Network Training with Approximate Tensor Operations. CoRR, abs/1805.08079.
, - . , . "".