أقدم لكم ترجمة فصل من كتاب علم البيانات العملي مع أناكوندا
"تحليلات البيانات التنبؤية - النمذجة والتحقق"
هدفنا الرئيسي في إجراء تحليلات البيانات المختلفة هو البحث عن أنماط للتنبؤ بما قد يحدث في المستقبل. بالنسبة لسوق الأوراق المالية ، يجري الباحثون والخبراء اختبارات مختلفة لفهم آليات السوق. في هذه الحالة ، يمكنك طرح الكثير من الأسئلة. ماذا سيكون مستوى مؤشر السوق في السنوات الخمس المقبلة؟ ماذا سيكون النطاق السعري التالي لشركة IBM؟ هل سيزداد تقلب السوق أو ينقص في المستقبل؟ ماذا يمكن أن يكون التأثير إذا غيرت الحكومات سياساتها الضريبية؟ ما هي المكاسب والخسائر المحتملة إذا بدأت دولة حربا تجارية مع دولة أخرى؟ كيف نتنبأ بسلوك المستهلك من خلال تحليل بعض المتغيرات ذات الصلة؟ هل يمكننا توقع احتمالية تخرج طالب الدراسات العليا بنجاح؟ هل يمكننا إيجاد علاقة بين السلوك المحدد لمرض معين؟
لذلك ، سننظر في المواضيع التالية:
- فهم تحليل البيانات التنبؤية
- مجموعات بيانات مفيدة
- التنبؤ بالأحداث المستقبلية
- اختيار النموذج
- اختبار جرانجر السببي
فهم تحليل البيانات التنبؤية
قد يكون لدى الناس العديد من الأسئلة بخصوص الأحداث المستقبلية.
- المستثمر ، إذا استطاع التنبؤ بالحركة المستقبلية لأسعار الأسهم ، يمكنه تحقيق ربح كبير.
- إذا تمكنت الشركات من توقع اتجاه منتجاتها ، فيمكنها زيادة سعر سهمها وحصتها في السوق.
- إذا تمكنت الحكومات من التنبؤ بأثر شيخوخة السكان على المجتمع والاقتصاد ، فسيكون لديها المزيد من الحوافز لتطوير سياسات أفضل من حيث ميزانية الدولة والقرارات الاستراتيجية الأخرى ذات الصلة.
- الجامعات ، إذا كان بإمكانهم فهم طلب السوق جيدًا من حيث الجودة والمهارات المحددة لخريجيهم ، فيمكنهم تطوير مجموعة من البرامج الأفضل أو إطلاق برامج جديدة لتلبية احتياجات القوى العاملة في المستقبل.
من أجل تشخيص أفضل ، يجب على الباحثين النظر في العديد من الأسئلة. على سبيل المثال ، هل بيانات العينة صغيرة جدًا؟ كيفية إزالة المتغيرات المفقودة؟ هل مجموعة البيانات هذه متحيزة من حيث إجراءات جمع البيانات؟ كيف نشعر بشأن التطرف أو الانبعاثات؟ ما هي الموسمية وكيف نتعامل معها؟ ما النماذج التي يجب أن نستخدمها؟ سيتناول هذا الفصل بعض هذه القضايا. لنبدأ بمجموعة بيانات مفيدة.
مجموعات بيانات مفيدة
أحد أفضل مصادر البيانات هو
مستودع تعلم الآلة UCI . بعد زيارة الموقع سنرى القائمة التالية:

على سبيل المثال ، إذا قمت بتحديد مجموعة البيانات الأولى (أذن البحر) ، فسوف نرى ما يلي. لتوفير المساحة ، يتم عرض الجزء العلوي فقط:

من هنا ، يمكن للمستخدمين تنزيل مجموعة البيانات والعثور على تعريفات متغيرة. يمكن استخدام الكود التالي لتحميل مجموعة البيانات:
dataSet<-"UCIdatasets" path<-"http://canisius.edu/~yany/RData/" con<-paste(path,dataSet,".RData",sep='') load(url(con)) dim(.UCIdatasets) head(.UCIdatasets)
يظهر الناتج المقابل هنا:

من الاستنتاج السابق ، نعلم أنه توجد في مجموعة البيانات 427 ملاحظة (مجموعات البيانات). لكل منها ، لدينا 7 وظائف ذات صلة ، مثل
الاسم و Data_Types و Default_Task و Attribute_Types و N_Instance (عدد الحالات) و
N_Attributes (عدد السمات)
والسنة . يمكن تفسير متغير يسمى
Default_Task على أنه الاستخدام الرئيسي لكل مجموعة بيانات. على سبيل المثال ، يمكن استخدام مجموعة بيانات أولى تسمى
Abalone في
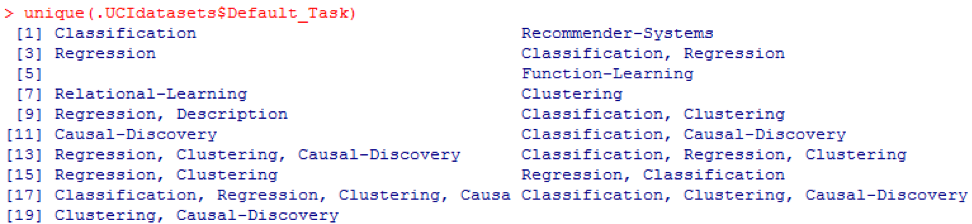
التصنيف . يمكن استخدام وظيفة
() الفريدة للبحث عن جميع مهام
Default_Task الممكنة الموضحة هنا:
حزمة R AppliedPredictiveModeling
تتضمن هذه الحزمة العديد من مجموعات البيانات المفيدة التي يمكن استخدامها لهذا الفصل وغيرها. أسهل طريقة للعثور على مجموعات البيانات هذه هي عن طريق وظيفة
help () الموضحة هنا:
library(AppliedPredictiveModeling) help(package=AppliedPredictiveModeling)
نعرض هنا بعض الأمثلة لتحميل مجموعات البيانات هذه. لتحميل مجموعة بيانات واحدة ، نستخدم الدالة
data () . بالنسبة لمجموعة البيانات الأولى المسماة
أذن البحر ، لدينا الكود التالي:
library(AppliedPredictiveModeling) data(abalone) dim(abalone) head(abalone)
الإخراج كما يلي:

في بعض الأحيان ، تتضمن مجموعة بيانات كبيرة عدة مجموعات بيانات فرعية:
library(AppliedPredictiveModeling) data(solubility) ls(pattern="sol")
[1] "solTestX" "solTestXtrans" "solTestY" [4] "solTrainX" "solTrainXtrans" "solTrainY"
لتحميل كل مجموعة بيانات ، يمكننا استخدام الوظائف
dim () والرأس () والذيل () والملخص () .
تحليلات السلاسل الزمنية
يمكن تعريف السلاسل الزمنية على أنها مجموعة من القيم التي يتم الحصول عليها في لحظات متتالية من الزمن ، غالبًا بفترات متساوية بينها. هناك فترات مختلفة ، مثل السنوية والفصلية والشهرية والأسبوعية واليومية. بالنسبة للسلسلة الزمنية للناتج المحلي الإجمالي (الناتج المحلي الإجمالي) ، نستخدم عادةً ربع سنويًا أو سنويًا. لعروض الأسعار - الترددات السنوية والشهرية واليومية. باستخدام الكود التالي ، يمكننا الحصول على بيانات الناتج المحلي الإجمالي للولايات المتحدة كل ربع سنة ولفترة سنوية:
ath<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPannual)
YEAR GDP 1 1930 92.2 2 1931 77.4 3 1932 59.5 4 1933 57.2 5 1934 66.8 6 1935 74.3
dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPquarterly)
DATE GDP_CURRENT GDP2009DOLLAR 1 1947Q1 243.1 1934.5 2 1947Q2 246.3 1932.3 3 1947Q3 250.1 1930.3 4 1947Q4 260.3 1960.7 5 1948Q1 266.2 1989.5 6 1948Q2 272.9 2021.9
ومع ذلك ، لدينا العديد من الأسئلة لتحليل السلاسل الزمنية. على سبيل المثال ، من وجهة نظر الاقتصاد الكلي ، لدينا دورات تجارية أو اقتصادية. قد يكون للصناعات أو الشركات الموسمية. على سبيل المثال ، باستخدام الصناعة الزراعية ، سوف ينفق المزارعون أكثر في فصلي الربيع والخريف وأقل في الشتاء. بالنسبة لتجار التجزئة ، سيكون لديهم تدفق هائل من الأموال في نهاية العام.
لمعالجة السلسلة الزمنية ، يمكننا استخدام العديد من الميزات المفيدة المضمنة في حزمة R ، والتي تسمى
timeSeries . في المثال ، نأخذ متوسط البيانات اليومية بتردد أسبوعي:
library(timeSeries) data(MSFT) x <- MSFT by <- timeSequence(from = start(x), to = end(x), by = "week") y<-aggregate(x,by,mean)
يمكننا أيضًا استخدام الدالة
head () لرؤية بعض الملاحظات:
head(x)
GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-09-28 60.8125 61.8750 60.6250 61.3125 26180200 2000-09-29 61.0000 61.3125 58.6250 60.3125 37026800 2000-10-02 60.5000 60.8125 58.2500 59.1250 29281200 2000-10-03 59.5625 59.8125 56.5000 56.5625 42687000 2000-10-04 56.3750 56.5625 54.5000 55.4375 68226700
head(y)
GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-10-04 59.6500 60.0750 57.7000 58.5500 40680380 2000-10-11 54.9750 56.4500 54.1625 55.0875 36448900 2000-10-18 53.0375 54.2500 50.8375 52.1375 50631280 2000-10-25 61.7875 64.1875 60.0875 62.3875 86457340 2000-11-01 66.1375 68.7875 65.8500 67.9375 53496000
التنبؤ بالأحداث المستقبلية
هناك العديد من الطرق التي يمكننا استخدامها عند محاولة التنبؤ بالمستقبل ، مثل المتوسط المتحرك ، والانحدار ، والانحدار الذاتي ، وما إلى ذلك. أولاً ، فلنبدأ بالأسهل للمتوسط المتحرك:
movingAverageFunction<- function(data,n=10){ out= data for(i in n:length(data)){ out[i] = mean(data[(i-n+1):i]) } return(out) }
في الكود السابق ، القيمة الافتراضية لعدد الفترات هي 10. يمكننا استخدام مجموعة بيانات تسمى MSFT مضمنة في حزمة R تسمى
timeSeries (انظر الكود التالي):
library(timeSeries) data(MSFT) p<-MSFT$Close
[1] 60.6250 61.3125 60.3125 59.1250 56.5625 55.4375
head(ma)
[1] 60.62500 61.31250 60.75000 60.25000 58.66667 57.04167
mean(p[1:3])
[1] 60.75
mean(p[2:4])
[1] 60.25
في الوضع اليدوي ، نجد أن متوسط القيم الثلاث الأولى لـ
x يطابق القيمة الثالثة لـ
y . بطريقة ما ، يمكننا استخدام المتوسط المتحرك للتنبؤ بالمستقبل.
في المثال التالي ، سنوضح كيفية تقييم عوائد السوق المتوقعة العام المقبل. هنا نستخدم مؤشر S & P500 والمتوسط السنوي للقيمة السنوية كقيمنا المتوقعة. يتم استخدام الأوامر القليلة الأولى لتحميل مجموعة بيانات ذات صلة تسمى
.sp500monthly . الغرض من البرنامج هو تقييم المتوسط السنوي وفاصل الثقة 90 في المائة:
library(data.table) path<-'http://canisius.edu/~yany/RData/' dataSet<-'sp500monthly.RData' link<-paste(path,dataSet,sep='') load(url(link))
[min mean max ]
cat(min2,ourMean,max2,"\n")
0.05032956 0.09022369 0.1301178
كما ترى من النتائج ، فإن المتوسط السنوي للعائد السنوي لمؤشر S & P500 هو 9٪. لكن لا يمكننا القول أن ربحية المؤشر العام المقبل ستكون 9٪ ، لأن يمكن أن يكون من 5٪ إلى 13٪ ، وهذه تقلبات كبيرة.
موسمية
في المثال التالي ، نظهر استخدام الارتباط الذاتي. أولاً ،
ننزل حزمة R تسمى
astsa ، والتي تعني تحليل السلاسل الزمنية الإحصائية التطبيقية. ثم نقوم بتحميل الناتج المحلي الإجمالي للولايات المتحدة بوتيرة ربع سنوية:
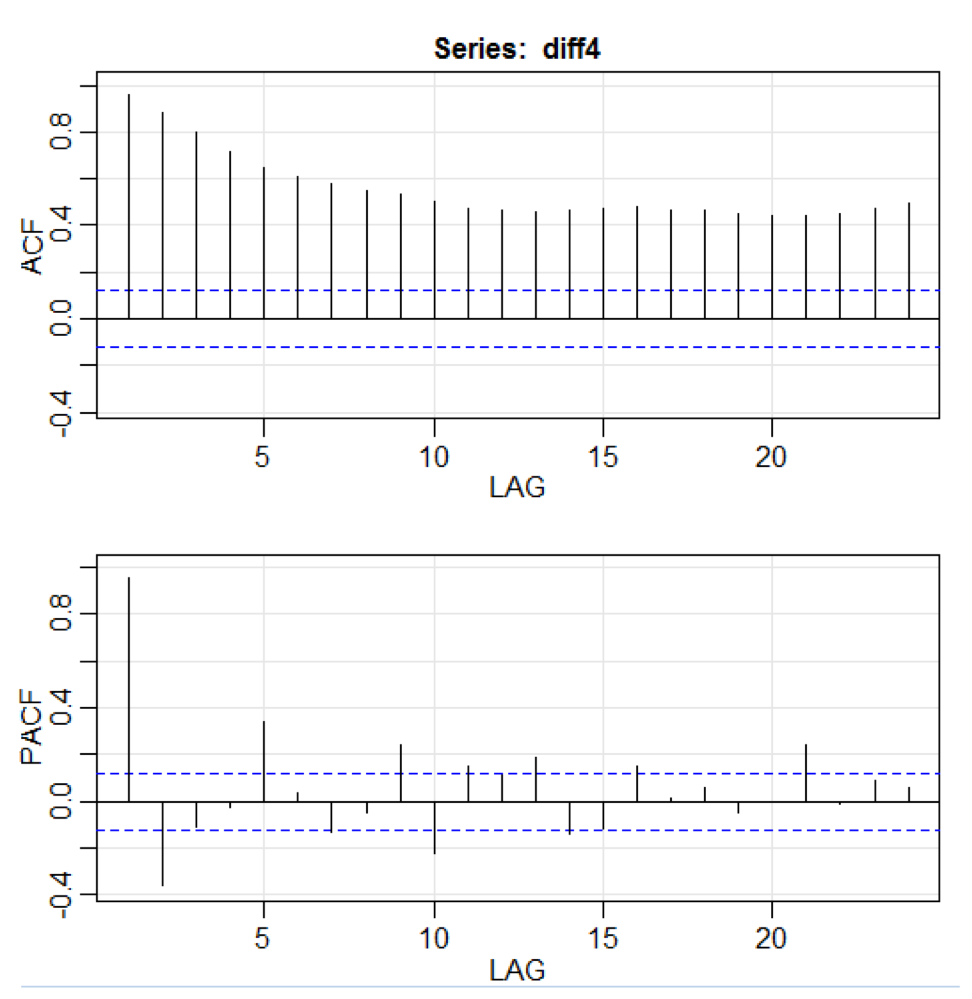
library(astsa) path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) x<-.usGDPquarterly$DATE y<-.usGDPquarterly$GDP_CURRENT plot(x,y) diff4 = diff(y,4) acf2(diff4,24)
في التعليمة البرمجية أعلاه ، تقبل الدالة
diff () الفرق ، على سبيل المثال ، القيمة الحالية مطروحًا منها القيمة السابقة. تشير قيمة الإدخال الثانية إلى تأخير. يتم استخدام دالة تسمى
acf2 () لإنشاء وطباعة السلاسل الزمنية ACF و PACF. يرمز ACF إلى دالة التباين الذاتي ، و PACF إلى وظيفة الارتباط الذاتي الجزئي. يتم عرض الرسوم البيانية ذات الصلة هنا:
تصور المكون
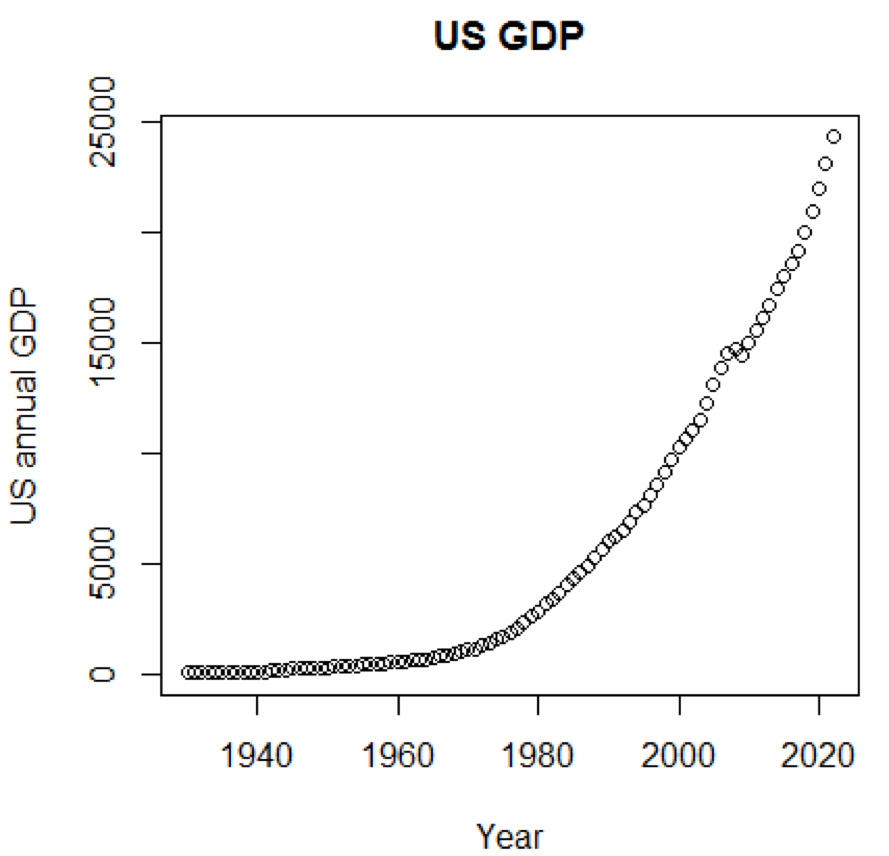
من الواضح أن المفاهيم ومجموعات البيانات ستكون مفهومة أكثر بكثير إذا تمكنا من استخدام الرسوم البيانية. يوضح المثال الأول التقلبات في الناتج المحلي الإجمالي للولايات المتحدة على مدى العقود الخمسة الماضية:
path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) title<-"US GDP" xTitle<-"Year" yTitle<-"US annual GDP" x<-.usGDPannual$YEAR y<-.usGDPannual$GDP plot(x,y,main=title,xlab=xTitle,ylab=yTitle)
يظهر الجدول المقابل هنا:
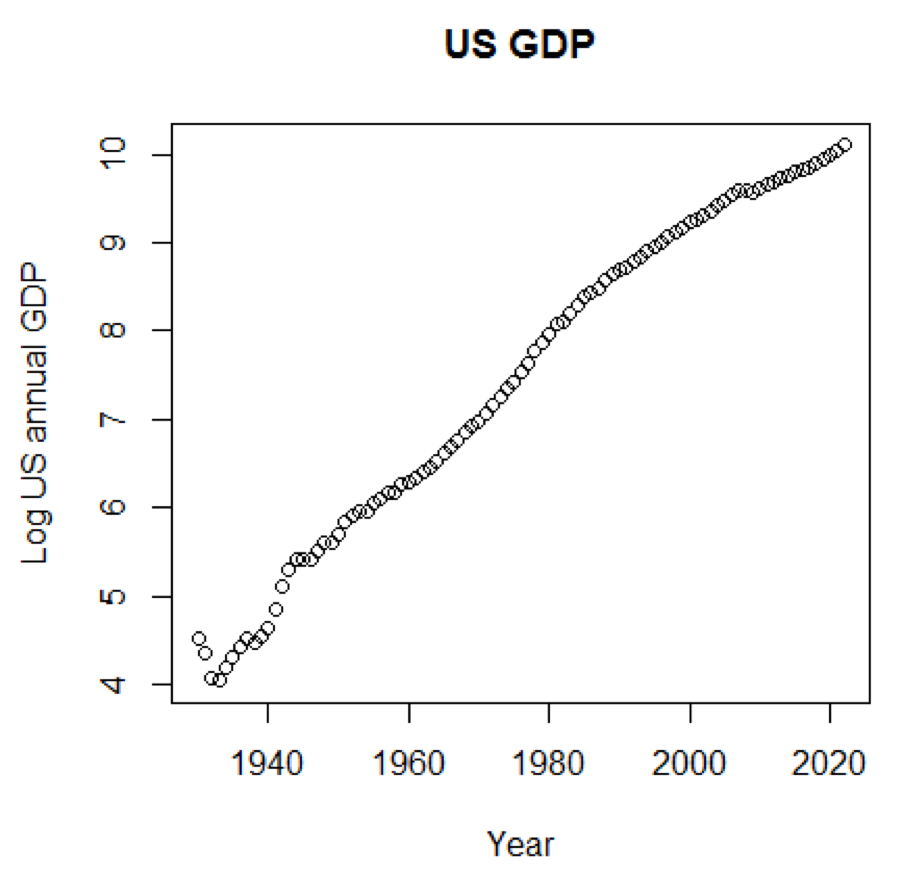
إذا استخدمنا المقياس اللوغاريتمي للناتج المحلي الإجمالي ، فسيكون لدينا الرمز والرسم البياني التالي:
yTitle<-"Log US annual GDP" plot(x,log(y),main=title,xlab=xTitle,ylab=yTitle)
المخطط التالي قريب من خط مستقيم:
حزمة R - LiblineaR
هذه الحزمة هي نموذج تنبؤي خطي يعتمد على مكتبة LIBLINEAR C / C ++. فيما يلي مثال على استخدام مجموعة بيانات
القزحية . يحاول البرنامج التنبؤ بالفئة التي ينتمي إليها النبات باستخدام بيانات التدريب:
library(LiblineaR) data(iris) attach(iris) x=iris[,1:4] y=factor(iris[,5]) train=sample(1:dim(iris)[1],100) xTrain=x[train,];xTest=x[-train,] yTrain=y[train]; yTest=y[-train] s=scale(xTrain,center=TRUE,scale=TRUE)
الاستنتاج على النحو التالي. BCR هو معدل تصنيف متوازن. لهذا الرهان ، كلما كان ذلك أفضل:
cat("Best model type is:",bestType,"\n")
Best model type is: 4
cat("Best cost is:",bestCost,"\n")
Best cost is: 1
cat("Best accuracy is:",bestAcc,"\n")
Best accuracy is: 0.98
print(res) yTest setosa versicolor virginica setosa 16 0 0 versicolor 0 17 0 virginica 0 3 14 print(BCR)
[1] 0.95
حزمة R - الكسوف
هذه الحزمة عبارة عن تجمع متوسط التوجه للنماذج التنبؤية المفسرة في البيانات عالية الأبعاد. أولاً ، دعنا نلقي نظرة على مجموعة بيانات تسمى
simdata تحتوي على بيانات محاكاة لحزمة:
library(eclust) data("simdata") dim(simdata)
[1] 100 502
simdata[1:5, 1:6]
YE Gene1 Gene2 Gene3 Gene4 [1,] -94.131497 0 -0.4821629 0.1298527 0.4228393 0.36643188 [2,] 7.134990 0 -1.5216289 -0.3304428 -0.4384459 1.57602830 [3,] 1.974194 0 0.7590055 -0.3600983 1.9006443 -1.47250061 [4,] -44.855010 0 0.6833635 1.8051352 0.1527713 -0.06442029 [5,] 23.547378 0 0.4587626 -0.3996984 -0.5727255 -1.75716775
table(simdata[,"E"])
0 1 50 50
يوضح الاستنتاج السابق أن بُعد البيانات هو 100 × 502.
Y هو ناقل الاستجابة المستمر ، و
E هو متغير البيئة الثنائية لطريقة ECLUST.
E = 0 للغير مكشوف (n = 50) و
E = 1 للكشف (n = 50).
يقوم البرنامج التالي R بتقييم تحويل Fisher z:
library(eclust) data("simdata") X = simdata[,c(-1,-2)] firstCorr<-cor(X[1:50,]) secondCorr<-cor(X[51:100,]) score<-u_fisherZ(n0=100,cor0=firstCorr,n1=100,cor1=secondCorr) dim(score)
[1] 500 500
score[1:5,1:5]
Gene1 Gene2 Gene3 Gene4 Gene5 Gene1 1.000000 -8.062020 6.260050 -8.133437 -7.825391 Gene2 -8.062020 1.000000 9.162208 -7.431822 -7.814067 Gene3 6.260050 9.162208 1.000000 8.072412 6.529433 Gene4 -8.133437 -7.431822 8.072412 1.000000 -5.099261 Gene5 -7.825391 -7.814067 6.529433 -5.099261 1.000000
نحدد تحويل فيشر z. بافتراض أن لدينا مجموعة من أزواج
n x i و
y i ، يمكننا تقدير ارتباطها باستخدام الصيغة التالية:
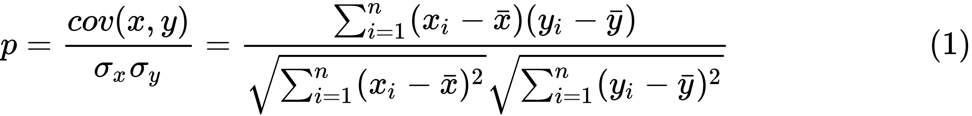 p
p هنا هو الارتباط بين متغيرين ، و

و
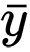
هي وسيلة نموذجية للمتغيرات العشوائية
x و
y . يتم تعريف قيمة
z على النحو التالي:
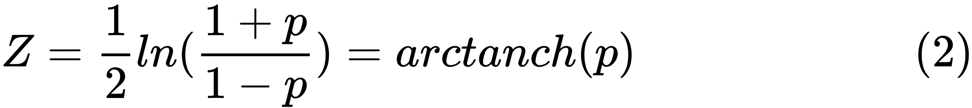 ln
ln هي دالة اللوغاريتم الطبيعي ، و
arctanh () هي دالة المماس الزائدية العكسية.
اختيار النموذج
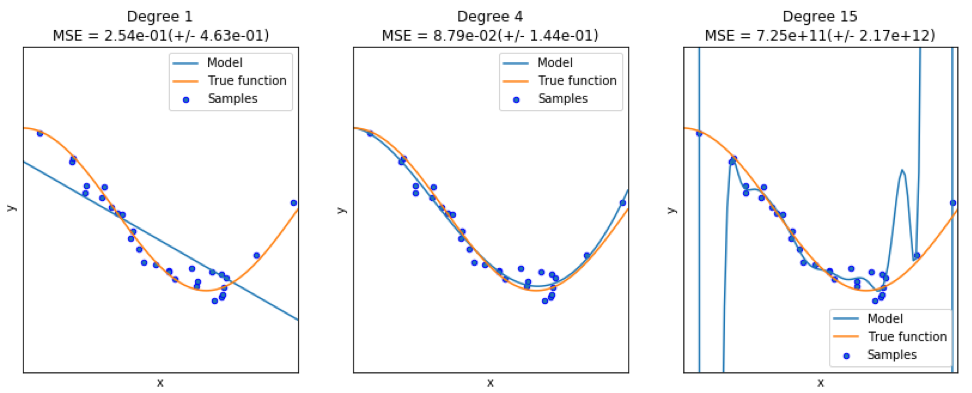
عند العثور على نموذج جيد ، نواجه أحيانًا نقصًا / فائضًا في البيانات. تم استعارة المثال التالي
من هنا . يوضح مشاكل العمل مع هذا وكيف يمكننا استخدام الانحدار الخطي مع ميزات كثيرة الحدود لتقريب الوظائف غير الخطية. الوظيفة المحددة:
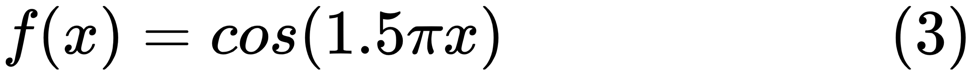
في البرنامج التالي ، نحاول استخدام نماذج خطية ومتعددة الحدود لتقريب معادلة. يظهر رمز معدل قليلاً هنا. يوضح البرنامج تأثير نقص البيانات / العرض الزائد على النموذج:
import sklearn import numpy as np import matplotlib.pyplot as plt from sklearn.pipeline import Pipeline from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression from sklearn.model_selection import cross_val_score
تظهر الرسوم البيانية الناتجة هنا:
حزمة بايثون - نموذج المنصة
يمكن العثور على مثال
هنا .
تظهر الأسطر القليلة الأولى من التعليمات البرمجية هنا:
import datetime import pandas from sqlalchemy import create_engine from metta import metta_io as metta from catwalk.storage import FSModelStorageEngine, CSVMatrixStore from catwalk.model_trainers import ModelTrainer from catwalk.predictors import Predictor from catwalk.evaluation import ModelEvaluator from catwalk.utils import save_experiment_and_get_hash help(FSModelStorageEngine)
يظهر الاستنتاج المقابل هنا. لتوفير المساحة ، يتم تقديم الجزء العلوي فقط:
Help on class FSModelStorageEngine in module catwalk.storage: class FSModelStorageEngine(ModelStorageEngine) | Method resolution order: | FSModelStorageEngine | ModelStorageEngine | builtins.object | | Methods defined here: | | __init__(self, *args, **kwargs) | Initialize self. See help(type(self)) for accurate signature. | | get_store(self, model_hash) | | ----------------------------------------------------------------------
| Data descriptors inherited from ModelStorageEngine: | | __dict__ | dictionary for instance variables (if defined) | | __weakref__ | list of weak references to the object (if defined)
حزمة بايثون - sklearn
نظرًا لأن
sklearn هي حزمة مفيدة جدًا ، يجدر إظهار المزيد من الأمثلة على استخدام هذه الحزمة. يوضح المثال الموضح هنا كيفية استخدام الحزمة لتصنيف المستندات حسب الموضوع باستخدام نهج مجموعة الكلمات.
يستخدم هذا المثال مصفوفة
scipy.sparse لتخزين الكائنات ويوضح المصنفات المختلفة التي يمكنها معالجة المصفوفات المتفرقة بكفاءة. يستخدم هذا المثال مجموعة بيانات من 20 مجموعة أخبار. سيتم تنزيله تلقائيًا ثم تخزينه مؤقتًا. يحتوي الملف المضغوط على ملفات إدخال ويمكن تنزيلها من
هنا . الكود متاح
هنا . لتوفير المساحة ، يتم عرض الأسطر القليلة الأولى فقط:
import logging import numpy as np from optparse import OptionParser import sys from time import time import matplotlib.pyplot as plt from sklearn.datasets import fetch_20newsgroups from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.feature_extraction.text import HashingVectorizer from sklearn.feature_selection import SelectFromModel
يظهر الناتج المقابل هنا:
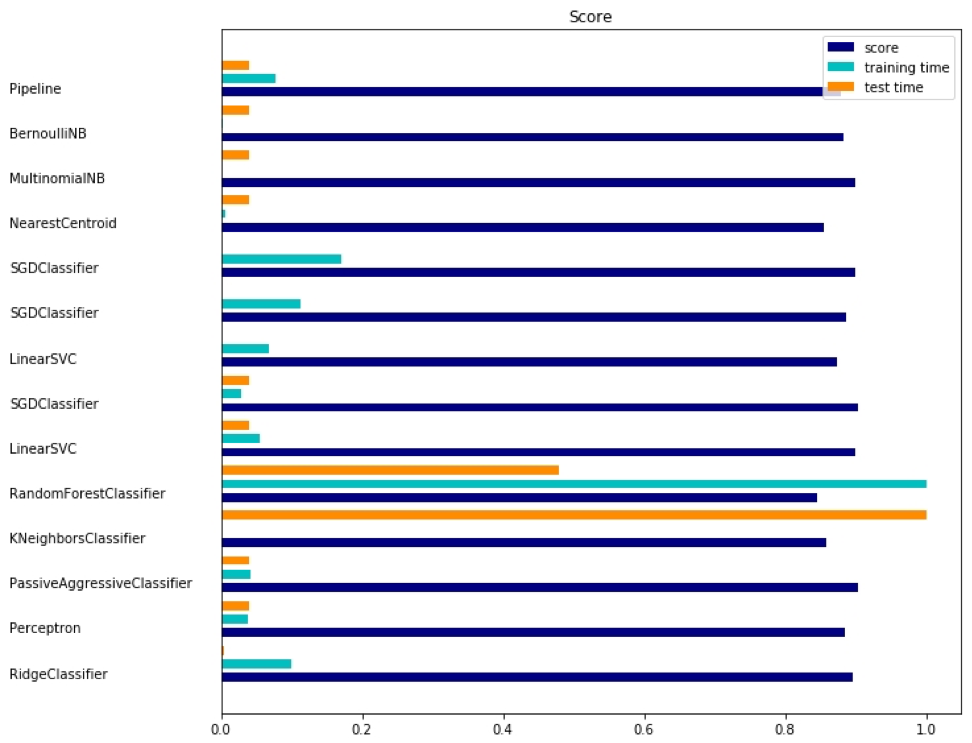
هناك ثلاثة مؤشرات لكل طريقة: التقييم ووقت التدريب ووقت الاختبار.
حزمة جوليا - QuantEcon
خذ على سبيل المثال استخدام سلاسل ماركوف:
using QuantEcon P = [0.4 0.6; 0.2 0.8]; mc = MarkovChain(P) x = simulate(mc, 100000); mean(x .== 1)
النتيجة:
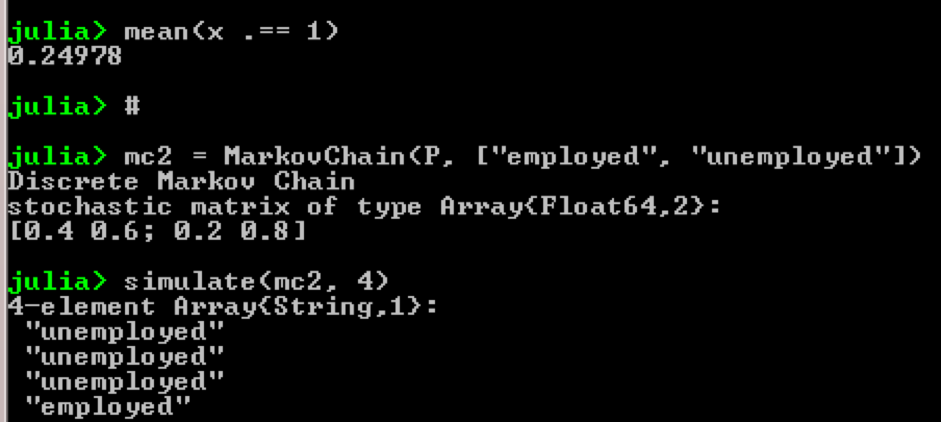
الغرض من المثال هو معرفة كيف يتحول شخص من وضع اقتصادي في المستقبل إلى وضع آخر. أولاً ، دعنا نلقي نظرة على الرسم البياني التالي:
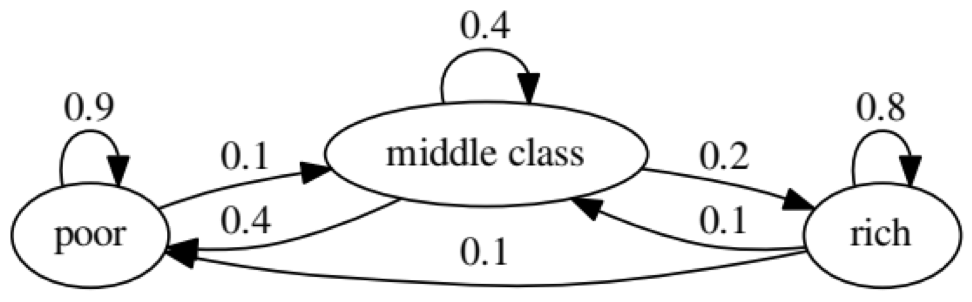
دعونا ننظر إلى أقصى اليسار بيضاوي مع الحالة "الفقيرة". 0.9 يعني أن الشخص الذي لديه هذا الوضع لديه فرصة 90 ٪ للبقاء فقيرا ، و 10 ٪ يذهبون إلى الطبقة المتوسطة. يمكن تمثيله بالمصفوفة التالية ، الأصفار حيث لا توجد حافة بين العقد:
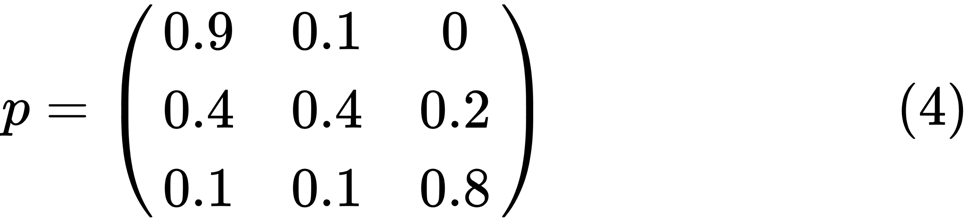
يقال أن حالتين ، x و y ، مرتبطتان ببعضهما إذا كان هناك أعداد صحيحة موجبة j و k ، مثل:

تسمى سلسلة ماركوف
P غير قابلة للاختزال إذا كانت جميع الحالات متصلة ؛ أي ، إذا
تم الإبلاغ عن
س و
ص لكل (س ، ص). سيؤكد الرمز التالي هذا:
using QuantEcon P = [0.9 0.1 0.0; 0.4 0.4 0.2; 0.1 0.1 0.8]; mc = MarkovChain(P) is_irreducible(mc)
يمثل الرسم البياني التالي حالة متطرفة ، حيث ستكون الحالة المستقبلية للشخص الفقير 100 ٪ فقيرة:

سيؤكد الرمز التالي هذا أيضًا ، لأن النتيجة ستكون
خاطئة :
using QuantEcon P2 = [1.0 0.0 0.0; 0.1 0.8 0.1; 0.0 0.2 0.8]; mc2 = MarkovChain(P2) is_irreducible(mc2)
اختبار جرانجر السببي
يتم استخدام اختبار السببية Granger لتحديد ما إذا كانت سلسلة زمنية واحدة عاملاً وتوفر معلومات مفيدة للتنبؤ بالسلسلة الثانية. يستخدم الكود التالي
مجموعة بيانات تسمى
ChickEgg كتوضيح . تحتوي مجموعة البيانات على عمودين ، عدد الدجاج وعدد البيض ، مع طابع زمني:
library(lmtest) data(ChickEgg) dim(ChickEgg)
[1] 54 2
ChickEgg[1:5,]
chicken egg [1,] 468491 3581 [2,] 449743 3532 [3,] 436815 3327 [4,] 444523 3255 [5,] 433937 3156
السؤال هو ، هل يمكننا استخدام عدد البيض هذا العام للتنبؤ بعدد الدجاج في العام المقبل؟
إذا كان الأمر كذلك ، فسيكون عدد الدجاج هو سبب جرانجر لعدد البيض. إذا لم يكن الأمر كذلك ، فنحن نقول أن عدد الدجاجات ليس سببًا في جرانجر لعدد البيض. إليك الرمز المناسب:
library(lmtest) data(ChickEgg) grangertest(chicken~egg, order = 3, data = ChickEgg)
Granger causality test Model 1: chicken ~ Lags(chicken, 1:3) + Lags(egg, 1:3) Model 2: chicken ~ Lags(chicken, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 5.405 0.002966 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
في النموذج 1 ، نحاول استخدام تباطؤ الفراخ بالإضافة إلى تباطؤ البيض لشرح عدد الفراخ.
لأن قيمة
P صغيرة جدًا (وهي مهمة عند 0.01) ، نقول أن عدد البيض هو سبب Granger لعدد الدجاج.
يوضح الاختبار التالي أنه لا يمكن استخدام بيانات الدجاج للتنبؤ بالفترة التالية:
grangertest(egg~chicken, order = 3, data = ChickEgg)
Granger causality test Model 1: egg ~ Lags(egg, 1:3) + Lags(chicken, 1:3) Model 2: egg ~ Lags(egg, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 0.5916 0.6238
في المثال التالي ، نتحقق من ربحية IBM و S & P500 من أجل معرفة أنها سبب Granger لسبب آخر.
أولاً ، نحدد دالة العائد:
ret_f<-function(x,ticker=""){ n<-nrow(x) p<-x[,6] ret<-p[2:n]/p[1:(n-1)]-1 output<-data.frame(x[2:n,1],ret) name<-paste("RET_",toupper(ticker),sep='') colnames(output)<-c("DATE",name) return(output) }
>x<-read.csv("http://canisius.edu/~yany/data/ibmDaily.csv",header=T) ibmRet<-ret_f(x,"ibm") x<-read.csv("http://canisius.edu/~yany/data/^gspcDaily.csv",header=T) mktRet<-ret_f(x,"mkt") final<-merge(ibmRet,mktRet) head(final)
DATE RET_IBM RET_MKT 1 1962-01-03 0.008742545 0.0023956877 2 1962-01-04 -0.009965497 -0.0068887673 3 1962-01-05 -0.019694350 -0.0138730891 4 1962-01-08 -0.018750380 -0.0077519519 5 1962-01-09 0.011829467 0.0004340133 6 1962-01-10 0.001798526 -0.0027476933
الآن يمكن استدعاء الوظيفة بقيم الإدخال. الهدف من البرنامج هو اختبار ما إذا كان يمكننا استخدام تباطؤ السوق لشرح ربحية IBM. بنفس الطريقة ، نتحقق من شرح تأخر IBM في عائدات السوق:
library(lmtest) grangertest(RET_IBM ~ RET_MKT, order = 1, data =final)
Granger causality test Model 1: RET_IBM ~ Lags(RET_IBM, 1:1) + Lags(RET_MKT, 1:1) Model 2: RET_IBM ~ Lags(RET_IBM, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 24.002 9.729e-07 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
أظهرت النتائج أنه يمكن استخدام S & P500 لشرح ربحية IBM للفترة التالية ، حيث أنها ذات دلالة إحصائية عند 0.1٪. سيتحقق الكود التالي لمعرفة ما إذا كان تأخر IBM يشرح التغيير في S & P500:
grangertest(RET_MKT ~ RET_IBM, order = 1, data =final)
Granger causality test Model 1: RET_MKT ~ Lags(RET_MKT, 1:1) + Lags(RET_IBM, 1:1) Model 2: RET_MKT ~ Lags(RET_MKT, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 7.5378 0.006049 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
تشير النتيجة إلى أنه خلال هذه الفترة ، يمكن استخدام عوائد IBM لشرح S & P500 من الفترة التالية.