نظرة عامة على طريقة المتجه المرجعي لخوارزمية التعلم الآلي (SVM)

مقدمة

في هذه المقالة ، سوف نستكشف العديد من جوانب SVM:

• المكون النظري ل SVM ؛
• كيف تعمل الخوارزمية على عينات لا يمكن تقسيمها إلى فئات خطياً ؛
• مثال Python وتنفيذ الخوارزمية في مكتبة SciKit Learn.

في المقالات التالية ، سأحاول التحدث عن المكون الرياضي لهذه الخوارزمية.

كما تعلم ، تنقسم مهام التعلم الآلي إلى فئتين رئيسيتين - التصنيف والانحدار. اعتمادًا على أي من هذه المهام التي نواجهها ، ومجموعة البيانات التي لدينا لهذه المهمة ، نختار الخوارزمية التي نستخدمها.

يعد أسلوب أجهزة المتجهات الداعمة أو SVM (من أجهزة المتجهات الداعمة الإنجليزية) خوارزمية خطية مستخدمة في مشاكل التصنيف والانحدار. تستخدم هذه الخوارزمية على نطاق واسع في الممارسة ويمكن أن تحل المشكلات الخطية وغير الخطية. إن جوهر "آلات" نواقل الدعم بسيط: تقوم الخوارزمية بإنشاء خط أو سطح مفرط يقسم البيانات إلى فئات.

النظرية

تتمثل المهمة الرئيسية للخوارزمية في العثور على الخط الأكثر صحة ، أو سطح مفرط ، يقسم البيانات إلى فئتين. SVM هو خوارزمية تستقبل البيانات عند الإدخال وترجع مثل هذا الخط الفاصل.

خذ بعين الاعتبار المثال التالي. لنفترض أن لدينا مجموعة بيانات ، ونريد تصنيف المربعات الحمراء وفصلها عن الدوائر الزرقاء (لنفترض أنها إيجابية وسلبية). سيكون الهدف الرئيسي في هذه المهمة هو العثور على الخط "المثالي" الذي سيفصل بين هاتين الفئتين.



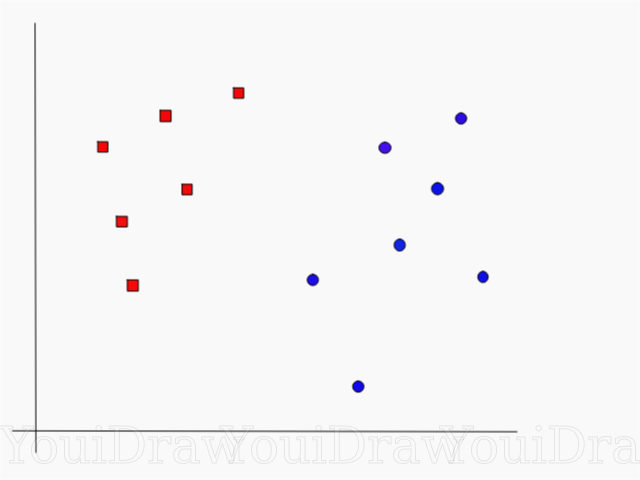
ابحث عن الخط المثالي ، أو السطح الزائد ، الذي يقسم مجموعة البيانات إلى فئتين زرقاء وحمراء.

للوهلة الأولى ، الأمر ليس بهذه الصعوبة ، أليس كذلك؟

ولكن ، كما ترون ، لا يوجد خط واحد فريد من نوعه يمكن أن يحل مثل هذه المشكلة. يمكننا اختيار عدد لا نهائي من الخطوط التي يمكن أن تفصل بين هاتين الفئتين. كيف يجد SVM بالضبط الخط "المثالي" ، وما هو "المثالي" في فهمه؟

ألقِ نظرة على المثال أدناه وفكر في أي من الخطين (الأصفر أو الأخضر) الذي يفصل بين الفئتين ، ويناسب وصف "مثالي"؟



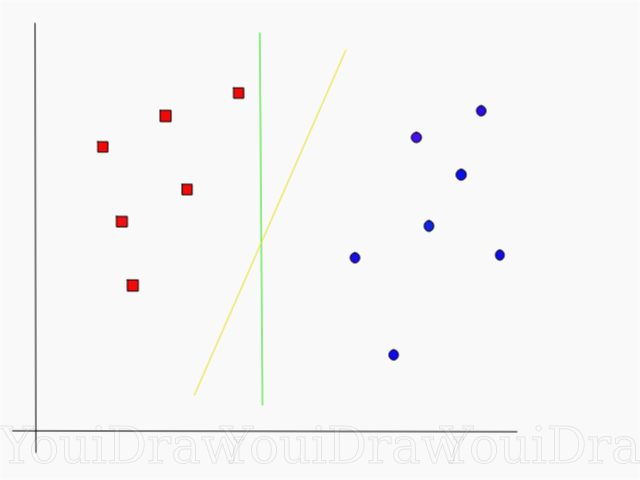
أي خط يفصل مجموعة البيانات بشكل أفضل في رأيك؟

إذا اخترت الخط الأصفر ، فأنا أهنئك: هذا هو الخط الذي ستختاره الخوارزمية. في هذا المثال ، يمكننا أن نفهم بشكل بديهي أن الخط الأصفر يفصل بين الفئتين وبالتالي يصنفهما أفضل من الفئة الخضراء.

في حالة الخط الأخضر - يقع بالقرب من الفئة الحمراء. على الرغم من حقيقة أنها صنفت جميع كائنات مجموعة البيانات الحالية بشكل صحيح ، فلن يتم تعميم مثل هذا الخط - لن يتصرف تمامًا مع مجموعة بيانات غير مألوفة. تعد مهمة العثور على فصل عام معمم بين إحدى المهام الرئيسية في التعلم الآلي.

كيف يجد SVM أفضل خط

تم تصميم خوارزمية SVM بطريقة تبحث عن نقاط على الرسم البياني تقع مباشرة إلى خط الفصل الأقرب. تسمى هذه النقاط بالنواقل المرجعية. ثم تقوم الخوارزمية بحساب المسافة بين نواقل الدعم ومستوى التقسيم. هذه هي المسافة التي تسمى الفجوة. الهدف الرئيسي من الخوارزمية هو زيادة مسافة الخلوص إلى أقصى حد. تعتبر أفضل طائرة زائدة هي طائرة زائدة تكون هذه الفجوة كبيرة قدر الإمكان.



بسيطة جدا ، أليس كذلك؟ خذ بعين الاعتبار المثال التالي ، مع مجموعة بيانات أكثر تعقيدًا لا يمكن تقسيمها خطياً.



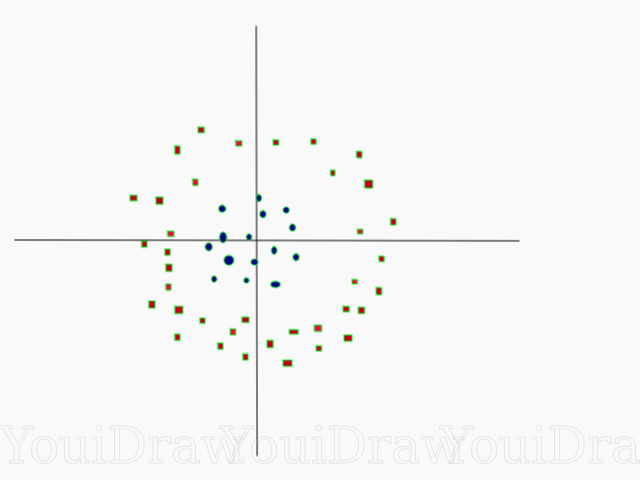
من الواضح أنه لا يمكن تقسيم مجموعة البيانات هذه بشكل خطي. لا يمكننا رسم خط مستقيم لتصنيف هذه البيانات. ولكن ، يمكن تقسيم مجموعة البيانات هذه خطياً بإضافة بُعد إضافي ، والذي سوف نسميه المحور Z. تخيل أن الإحداثيات على المحور Z يتم تنظيمها بواسطة القيود التالية:

$$

$$z = x² + y²$$

وهكذا ، يتم تمثيل الإحداثي Z من مربع مسافة النقطة إلى بداية المحور.
يوجد أدناه تصور لمجموعة البيانات نفسها على المحور Z.



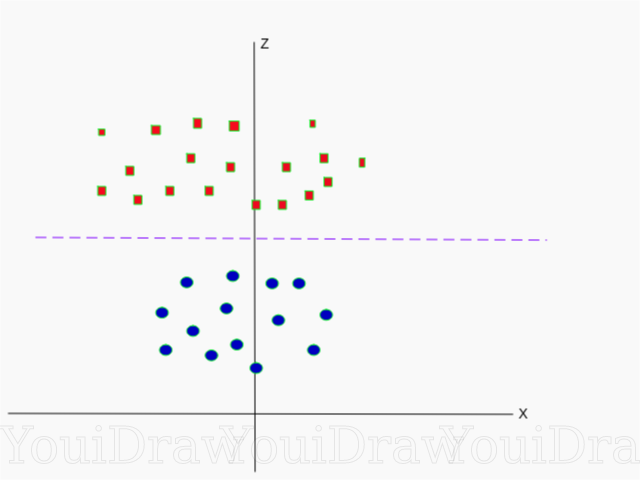
الآن يمكن تقسيم البيانات خطيا. افترض أن خط أرجواني يفصل البيانات z = k ، حيث k ثابت. إذا

$$

$$z = x² + y²$$

ثم

$$

$$k = x² + y²$$

- صيغة الدائرة. وبالتالي ، يمكننا عرض الفاصل الخطي الخاص بنا ، بالرجوع إلى العدد الأصلي لأبعاد العينة ، باستخدام هذا التحول.



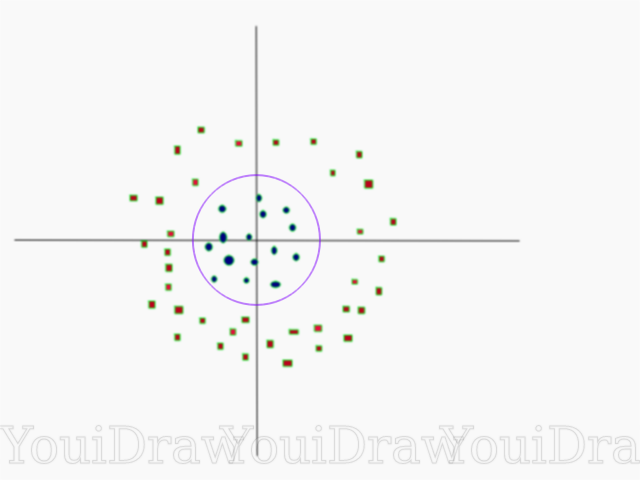
ونتيجة لذلك ، يمكننا تصنيف مجموعة بيانات غير خطية عن طريق إضافة بُعد إضافي إليها ، ثم إعادتها إلى شكلها الأصلي باستخدام التحويل الرياضي. ومع ذلك ، ليس مع جميع مجموعات البيانات من السهل تحريك مثل هذا التحول. لحسن الحظ ، فإن تنفيذ هذه الخوارزمية في مكتبة sklearn يحل هذه المشكلة بالنسبة لنا.

طائرة مفرطة

الآن بعد أن تعرّفنا على منطق الخوارزمية ، ننتقل إلى التعريف الرسمي للطائرة المفرطة

إن الطائرة الزائدة هي طائرة فرعية ذات أبعاد n-1 في مساحة إقليدية ذات أبعاد n تقسم المساحة إلى جزأين منفصلين.

على سبيل المثال ، تخيل أن خطنا يتم تمثيله كمسافة إقليدية أحادية البعد (أي أن مجموعة بياناتنا تقع على خط مستقيم). حدد نقطة على هذا الخط. ستقوم هذه النقطة بتقسيم مجموعة البيانات ، في حالتنا الخط ، إلى قسمين. يحتوي الخط على مقياس واحد ، والنقطة بها 0 مقاييس. لذلك ، فإن النقطة هي hyperplane من خط.

بالنسبة لمجموعة البيانات ثنائية الأبعاد التي التقينا بها سابقًا ، كان خط التقسيم هو نفس السطح الزائد. ببساطة ، للحصول على مساحة n-dimensional توجد طائرة مفردة n-1 مقسمة تقسم هذه المساحة إلى قسمين.

الكود

import numpy as np X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]]) y = np.array([1, 1, 2, 2]) 

يتم تمثيل النقاط كمصفوفة X ، والفئات التي تنتمي إليها كمصفوفة y.
الآن سنقوم بتدريب نموذجنا مع هذه العينة. في هذا المثال ، قمت بتعيين المعلمة الخطية لـ "kernel" للمصنف (kernel).

 from sklearn.svm import SVC clf = SVC(kernel='linear') clf = SVC.fit(X, y) 

التنبؤ الطبقي لكائن جديد

 prediction = clf.predict([[0,6]]) 

إعداد المعلمة

المعلمات هي الوسيطات التي تمررها عند إنشاء المصنف. فيما يلي قدمت بعض أهم إعدادات SVM المخصصة:

"C"

تساعد هذه المعلمة على ضبط هذا الخط الدقيق بين "النعومة" ودقة تصنيف الأشياء في عينة التدريب. كلما زادت قيمة "C" ، سيتم تصنيف المزيد من العناصر في مجموعة التدريب بشكل صحيح.



في هذا المثال ، هناك العديد من حدود القرار التي يمكننا تحديدها لهذه العينة المحددة. انتبه إلى عتبة القرار المباشرة (المعروضة على الرسم البياني كخط أخضر). إنه بسيط للغاية ، ولهذا السبب تم تصنيف العديد من الأشياء بشكل غير صحيح. تسمى هذه النقاط التي تم تصنيفها بشكل غير صحيح القيم المتطرفة في البيانات.

يمكننا أيضًا ضبط المعلمات بطريقة نحصل في النهاية على خط أكثر انحناء (عتبة القرار باللون الأزرق الفاتح) ، والذي سيصنف جميع بيانات عينة التدريب بشكل صحيح. بالطبع ، في هذه الحالة ، فإن فرص أن يتمكن نموذجنا من التعميم وإظهار نتائج جيدة بنفس القدر على البيانات الجديدة ضئيلة بشكل كارثي. لذلك ، إذا كنت تحاول تحقيق الدقة عند تدريب النموذج ، يجب أن تهدف إلى شيء أكثر مباشرة ، مباشرة. كلما زاد الرقم "C" ، زاد تشابك الطائرة الزائدة في نموذجك ، ولكن كلما زاد عدد العناصر المصنفة بشكل صحيح في مجموعة التدريب. لذلك ، من المهم "تحريف" معلمات النموذج لمجموعة بيانات محددة لتجنب إعادة التدريب ولكن ، في نفس الوقت ، تحقيق دقة عالية.

جاما

في الوثائق الرسمية ، تقول مكتبة SciKit Learn أن جاما تحدد مدى تأثير كل عنصر من عناصر مجموعة البيانات في تحديد "الخط المثالي". كلما انخفض جاما ، كلما زادت العناصر ، حتى تلك التي تكون بعيدة بما فيه الكفاية عن خط التقسيم ، تشارك في عملية اختيار هذا الخط. إذا كانت جاما عالية ، فإن الخوارزمية "ستعتمد" فقط على العناصر الأقرب إلى الخط نفسه.
إذا تم تعيين مستوى جاما مرتفعًا جدًا ، فلن تشارك سوى العناصر الأقرب إلى الخط في عملية صنع القرار في موقع الخط. هذا سوف يساعد على تجاهل القيم المتطرفة في البيانات. تم تصميم خوارزمية SVM بحيث يكون للنقاط الموجودة بالقرب من بعضها وزن أكبر عند اتخاذ القرار. ومع ذلك ، من خلال الإعدادات الصحيحة لـ "C" و "gamma" ، يمكن تحقيق نتيجة مثلى تبني سطحًا خطيًا أكثر تجاهلًا للقيم المتطرفة ، وبالتالي يمكن تعميمه بشكل أكبر.

الخلاصة

أتمنى مخلصًا أن تساعدك هذه المقالة على فهم جوهر عمل SVM أو طريقة Vector Vector. أتوقع منك أي تعليقات ونصائح. في المنشورات اللاحقة ، سأتحدث عن المكون الرياضي لمشاكل SVM والتحسين.

مصادر:
وثائق SVM الرسمية في SciKit Learn
مدونة TowardsDataScience
سراج رافال: دعم آلات المتجهات
مقدمة حول تعلم الآلة Udacity SVM: فيديو دورة غاما
ويكيبيديا: SVM