المصدر : Wikipedia Licence CC-BY-SA 3.0

إذا كنت كثيرًا ما تسافر بالمواصلات العامة ، فربما واجهت هذا الموقف:

انت تتوقف مكتوب أن الحافلة تعمل كل 10 دقائق. لاحظ الوقت ... وأخيرًا ، بعد 11 دقيقة ، وصلت الحافلة وفكرت: لماذا أنا دائمًا محظوظ؟

من الناحية النظرية ، إذا وصلت الحافلات كل 10 دقائق ، ووصلت في وقت عشوائي ، فيجب أن يكون متوسط ​​الانتظار حوالي 5 دقائق. ولكن في الواقع ، لا تصل الحافلات في الموعد المحدد ، لذا يمكنك الانتظار لفترة أطول. اتضح أنه ، مع بعض الافتراضات المعقولة ، يمكن للمرء أن يصل إلى استنتاج مذهل:

عند انتظار حافلة تصل في المتوسط ​​كل 10 دقائق ، سيكون متوسط ​​وقت الانتظار 10 دقائق.

هذا ما يسمى أحيانًا بمفارقة وقت الانتظار .

كانت لدي فكرة من قبل ، وكنت أتساءل دائمًا ما إذا كان هذا صحيحًا حقًا ... ما مدى توافق هذه "الافتراضات المعقولة" مع الواقع؟ في هذه المقالة ، ندرس مفارقة الكمون من حيث كل من النمذجة والحجج الاحتمالية ، ثم نلقي نظرة على بعض بيانات الحافلات الفعلية في سياتل لحل (على أمل) المفارقة مرة واحدة وإلى الأبد.

التفتيش المفارقة

إذا وصلت الحافلات بالضبط كل عشر دقائق ، فسيكون متوسط ​​وقت الانتظار 5 دقائق. يمكن للمرء أن يفهم بسهولة لماذا تؤدي إضافة الاختلافات إلى الفاصل الزمني بين الحافلات إلى زيادة متوسط ​​وقت الانتظار.

مفارقة وقت الانتظار هي حالة خاصة لظاهرة أكثر عمومية - مفارقة التفتيش ، والتي تمت مناقشتها بالتفصيل في مقالة ألن داوني المعقولة ، "مفارقة التفتيش في كل مكان حولنا" .

باختصار ، تنشأ مفارقة المعاينة كلما ارتبط احتمال ملاحظة كمية بالكمية المرصودة. يقدم ألن مثالاً لمسح لطلاب الجامعات حول متوسط ​​حجم فصولهم. على الرغم من أن المدرسة تتحدث بصدق عن متوسط ​​عدد الطلاب البالغ عددهم 30 طالبًا في المجموعة ، إلا أن متوسط ​​حجم المجموعة من وجهة نظر الطلاب أكبر بكثير. والسبب هو أنه في الفصول الكبيرة (بشكل طبيعي) هناك المزيد من الطلاب ، والذي تم الكشف عنه أثناء المسح.

في حالة جدول الحافلات بفاصل زمني مدته 10 دقائق ، يكون الفاصل الزمني بين الواصلين أحيانًا أطول من 10 دقائق ، وأحيانًا أقصر. وإذا توقفت في وقت عشوائي ، فمن المرجح أن تواجه فترة زمنية أطول من فترة أقصر. وبالتالي فمن المنطقي أن متوسط ​​الفاصل الزمني بين فترات الانتظار أطول من متوسط ​​الفاصل الزمني بين الحافلات ، لأن الفترات الأطول تكون أكثر شيوعًا في العينة.

لكن مفارقة الكمون تعطي تصريحًا أقوى: إذا كان متوسط ​​تباعد الحافلة هو $$$N$ دقيقة ، متوسط ​​وقت الانتظار للمسافرين $$$2N$ دقائق. هل يمكن أن يكون هذا صحيحا؟

محاكاة الكمون

لإقناع أنفسنا بمعقولية هذا ، نقوم أولاً بمحاكاة تدفق الحافلات التي تصل في المتوسط ​​10 دقائق. من أجل الدقة ، خذ عينة كبيرة: مليون حافلة (أو حوالي 19 عامًا من حركة المرور على مدار الساعة لمدة 10 دقائق):

import numpy as np N = 1000000 # number of buses tau = 10 # average minutes between arrivals rand = np.random.RandomState(42) # universal random seed bus_arrival_times = N * tau * np.sort(rand.rand(N)) 

تحقق من أن متوسط ​​الفاصل الزمني قريب من $$$\ tau = 10$ :

 intervals = np.diff(bus_arrival_times) intervals.mean() 

9.9999879601518398

يمكننا الآن محاكاة وصول عدد كبير من الركاب في محطة للحافلات خلال هذه الفترة الزمنية وحساب وقت الانتظار الذي يمر به كل منهم. قم بتغليف الكود في وظيفة لاستخدامه لاحقًا:

 def simulate_wait_times(arrival_times, rseed=8675309, # Jenny's random seed n_passengers=1000000): rand = np.random.RandomState(rseed) arrival_times = np.asarray(arrival_times) passenger_times = arrival_times.max() * rand.rand(n_passengers) # find the index of the next bus for each simulated passenger i = np.searchsorted(arrival_times, passenger_times, side='right') return arrival_times[i] - passenger_times 

ثم نقوم بمحاكاة وقت الانتظار وحساب المتوسط:

 wait_times = simulate_wait_times(bus_arrival_times) wait_times.mean() 

10.001584206227317

متوسط ​​وقت الانتظار يقترب من 10 دقائق ، كما تنبأت المفارقة.

التعمق أكثر: الاحتمالات وعمليات بواسون

كيف تحاكي مثل هذه الحالة؟

في الواقع ، هذا مثال على مفارقة التفتيش ، حيث يرتبط احتمال ملاحظة القيمة بالقيمة نفسها. دلالة بواسطة $$$p (T)$ التباعد $$$T$ بين الحافلات عند وصولهم إلى محطة الحافلات. في مثل هذا السجل ، ستكون القيمة المتوقعة لوقت الوصول هي:

$$

$$E [T] = \ int_0 ^ \ infty T ~ p (T) ~ dT$$

اخترنا في المحاكاة السابقة $$$E [T] = \ tau = 10$ دقائق.

عندما يصل الراكب إلى محطة الحافلات في أي وقت ، فإن احتمال وقت الانتظار لا يعتمد فقط على $$$p (T)$ ولكن أيضا من $$$T$ : كلما زاد الفاصل الزمني ، زاد عدد الركاب فيه.

وهكذا يمكننا كتابة توزيع وقت الوصول من وجهة نظر الركاب:

$$

$$p_ {exp} (T) \ propto T ~ p (T)$$

يشتق ثابت التناسب من تطبيع التوزيع:

$$

$$p_ {exp} (T) = \ frac {T ~ p (T)} {\ int_0 ^ \ infty T ~ p (T) ~ dT}$$

يبسط ل

$$

$$p_ {exp} (T) = \ frac {T ~ p (T)} {E [T]}$$

ثم وقت الانتظار $$$E [W]$ سيكون نصف الفاصل الزمني المتوقع للركاب ، حتى نتمكن من التسجيل

$$

$$E [W] = \ frac {1} {2} E_ {exp} [T] = \ frac {1} {2} \ int_0 ^ \ infty T ~ p_ {exp} (T) ~ dT$$

والتي يمكن إعادة كتابتها بطريقة مفهومة أكثر:

$$

$$E [W] = \ frac {E [T ^ 2]} {2E [T]}$$

والآن يبقى فقط لاختيار نموذج $$$p (T)$ وحساب التكاملات.

اختيار ص (T)

بعد أن حصلت على نموذج رسمي ، ما هو التوزيع المعقول لـ $$$p (T)$ ؟؟؟ سنرسم صورة التوزيع $$$p (T)$ ضمن وصولنا المقلد من خلال رسم رسم بياني للفترات الفاصلة بين الواصلين:

 %matplotlib inline import matplotlib.pyplot as plt plt.style.use('seaborn') plt.hist(intervals, bins=np.arange(80), density=True) plt.axvline(intervals.mean(), color='black', linestyle='dotted') plt.xlabel('Interval between arrivals (minutes)') plt.ylabel('Probability density'); 

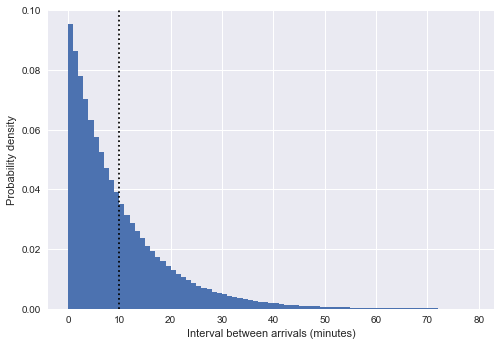
هنا ، يُظهر الخط المتقطع العمودي فاصل متوسط ​​يبلغ حوالي 10 دقائق. هذا يشبه إلى حد كبير التوزيع الأسي ، وليس عن طريق الصدفة: إن محاكاة وقت وصول الحافلة في شكل أرقام عشوائية موحدة قريبة جدًا من عملية بواسون ، وبالنسبة لهذه العملية ، يكون توزيع الفترات أسيًا.

(ملاحظة: في حالتنا ، هذا فقط أس تقريبي ؛ في الواقع ، الفواصل الزمنية $$$T$ بين $$$N$ نقاط مختارة بالتساوي خلال فترة زمنية $$$N \ tau$ توزيع مباراة بيتا $$$T / (N \ tau) \ sim \ mathrm {Beta} [1، N]$ وهو في الحد الأقصى $$$N$ يقترب $$$T \ sim \ mathrm {Exp} [1 / \ tau]$ . لمزيد من المعلومات ، يمكنك قراءة ، على سبيل المثال ، منشور على StackExchange أو هذا الموضوع على Twitter ).

يشير التوزيع الأسي للفواصل الزمنية إلى أن وقت الوصول يتبع عملية بواسون. للتحقق من هذا المنطق ، نتحقق من وجود خاصية أخرى لعملية بواسون: أن عدد الوافدين خلال فترة زمنية محددة هو توزيع بواسون. للقيام بذلك ، نقسم الوصول المقلد إلى كتل زمنية:

 from scipy.stats import poisson # count the number of arrivals in 1-hour bins binsize = 60 binned_arrivals = np.bincount((bus_arrival_times // binsize).astype(int)) x = np.arange(20) # plot the results plt.hist(binned_arrivals, bins=x - 0.5, density=True, alpha=0.5, label='simulation') plt.plot(x, poisson(binsize / tau).pmf(x), 'ok', label='Poisson prediction') plt.xlabel('Number of arrivals per hour') plt.ylabel('frequency') plt.legend(); 

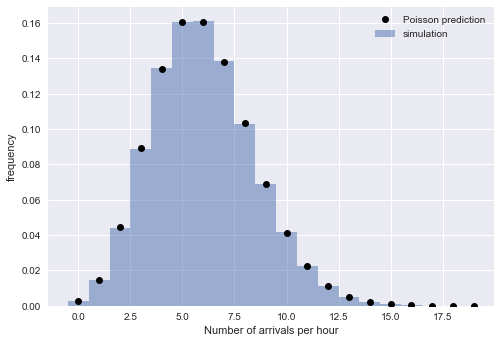
تقنعنا المراسلات الوثيقة بين القيم التجريبية والنظرية بصحة تفسيرنا: على نطاق واسع $$$N$ يتم وصف وقت الوصول المحاكي جيدًا من خلال عملية بواسون ، والتي تنطوي على فترات موزعة بشكل كبير.

هذا يعني أنه يمكن كتابة التوزيع الاحتمالي:

$$

$$p (T) = \ frac {1} {\ tau} e ^ {- T / \ tau}$$

إذا استبدلنا النتيجة في الصيغة السابقة ، فسوف نجد متوسط ​​وقت الانتظار للركاب في المحطة:

$$

$$E [W] = \ frac {\ int_0 ^ \ infty T ^ 2 ~ e ^ {- T / \ tau}} {2 \ int_0 ^ \ infty T ~ e ^ {- T / \ tau}} = \ frac {2 \ tau ^ 3} {2 (\ tau ^ 2)} = \ tau$$

بالنسبة للرحلات التي تصل من خلال عملية بواسون ، فإن وقت الانتظار المتوقع مطابق لمتوسط ​​الفترة الفاصلة بين القادمين.

يمكن مناقشة هذه المشكلة على النحو التالي: عملية بواسون هي عملية بدون ذاكرة ، أي أن تاريخ الأحداث ليس له علاقة بالوقت المتوقع للحدث التالي. لذلك ، عند الوصول إلى محطة للحافلات ، يكون متوسط ​​وقت الانتظار للحافلة هو نفسه دائمًا: في حالتنا ، تكون 10 دقائق ، بغض النظر عن مقدار الوقت المنقضي منذ الحافلة السابقة! لا يهم المدة التي كنت تنتظرها: الوقت المتوقع للحافلة التالية دائمًا هو 10 دقائق بالضبط: في عملية بواسون لا تحصل على "رصيد" للوقت الذي تقضيه في الانتظار.

مهلة الواقع

ما ورد أعلاه جيد إذا تم وصف وصول الحافلات الحقيقية بالفعل بواسطة عملية بواسون ، ولكن هل هذا صحيح؟


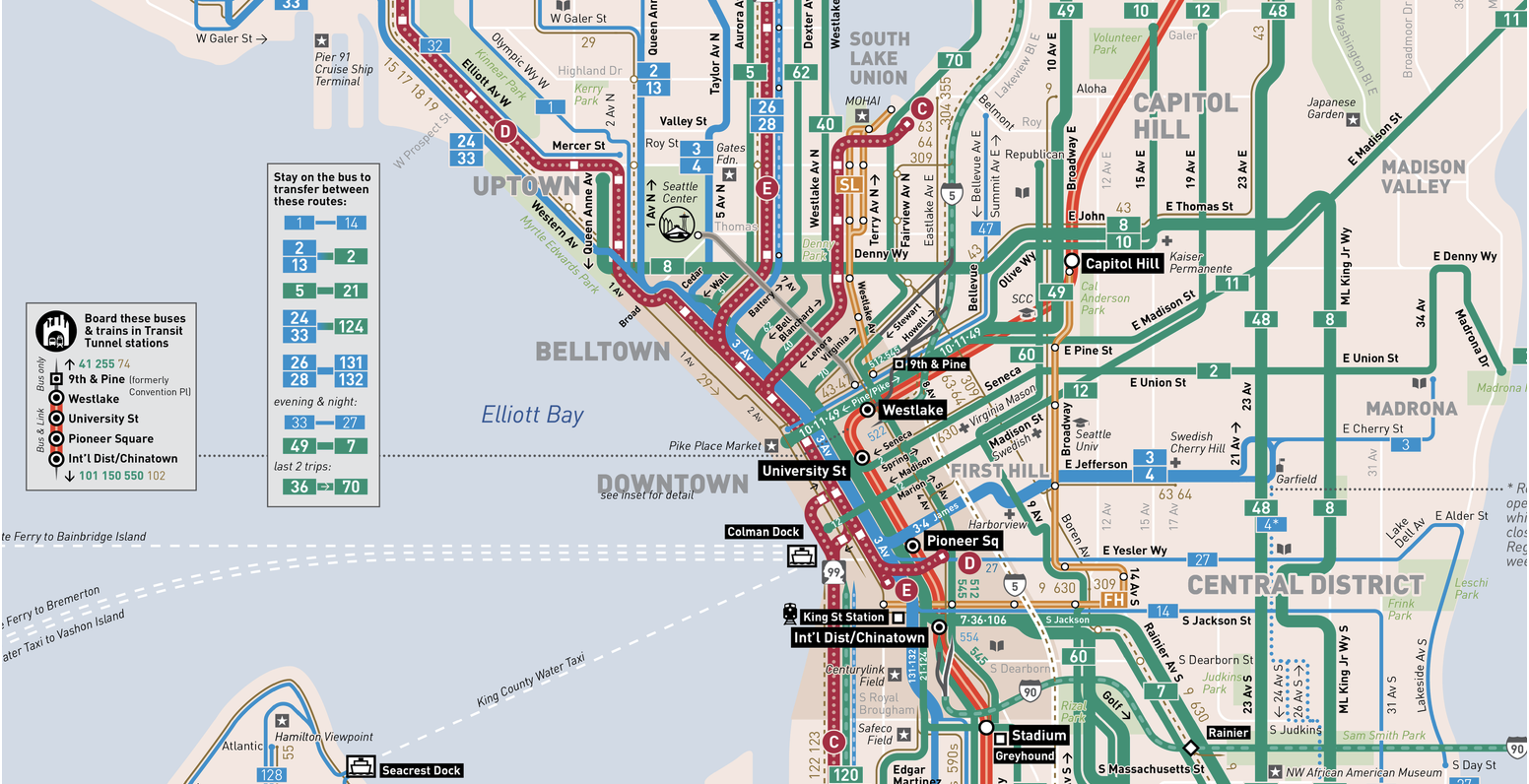المصدر: مخطط النقل العام في سياتل

دعونا نحاول تحديد مدى تناسق مفارقة وقت الانتظار مع الواقع. للقيام بذلك ، سنقوم بفحص بعض البيانات المتاحة للتنزيل هنا: arrival_times.csv (ملف 3 ميغابايت CSV). تحتوي مجموعة البيانات على أوقات الوصول المخططة والفعلية لحافلات RapidRide C و D و E في محطة الحافلات 3rd & Pike في وسط مدينة سياتل. تم تسجيل البيانات في الربع الثاني من عام 2016 (جزيل الشكر لمارك هالينباك من مركز النقل بولاية واشنطن لهذا الملف!).

 import pandas as pd df = pd.read_csv('arrival_times.csv') df = df.dropna(axis=0, how='any') df.head() 

	OPD_DATE	VEHICLE_ID	RTE	DIR	TRIP_ID	STOP_ID	STOP_NAME	SCH_STOP_TM	ACT_STOP_TM
0	2016-03-26	6201	673	ق	30908177	431	3RD AVE & PIKE ST (431)	01:11:57	01:13:19
1	2016-03-26	6201	673	ق	30908033	431	3RD AVE & PIKE ST (431)	23:19:57	23:16:13
2	2016-03-26	6201	673	ق	30908028	431	3RD AVE & PIKE ST (431)	21:19:57	21:18:46
3	2016-03-26	6201	673	ق	30908019	431	3RD AVE & PIKE ST (431)	19:04:57	19:01:49
4	2016-03-26	6201	673	ق	30908252	431	3RD AVE & PIKE ST (431)	16:42:57	16:42:39

اخترت بيانات RapidRide ، بما في ذلك لأنه في معظم اليوم تعمل الحافلات على فترات منتظمة من 10 إلى 15 دقيقة ، ناهيك عن حقيقة أنني مسافر متكرر للطريق C.

تطهير البيانات

أولاً ، سنقوم بتنظيف القليل من البيانات لتحويلها إلى عرض ملائم:

 # combine date and time into a single timestamp df['scheduled'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['SCH_STOP_TM']) df['actual'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['ACT_STOP_TM']) # if scheduled & actual span midnight, then the actual day needs to be adjusted minute = np.timedelta64(1, 'm') hour = 60 * minute diff_hrs = (df['actual'] - df['scheduled']) / hour df.loc[diff_hrs > 20, 'actual'] -= 24 * hour df.loc[diff_hrs < -20, 'actual'] += 24 * hour df['minutes_late'] = (df['actual'] - df['scheduled']) / minute # map internal route codes to external route letters df['route'] = df['RTE'].replace({673: 'C', 674: 'D', 675: 'E'}).astype('category') df['direction'] = df['DIR'].replace({'N': 'northbound', 'S': 'southbound'}).astype('category') # extract useful columns df = df[['route', 'direction', 'scheduled', 'actual', 'minutes_late']].copy() df.head() 

	الطريق	الاتجاه	الرسم البياني	حقيقة الوصول	التأخير (دقيقة)
0	ج	الجنوب	2016-03-26 01:11:57	2016-03-26 01:13:19	1.366667
1	ج	الجنوب	2016-03-26 23:19:57	2016-03-26 23:16:13	-3.733333
2	ج	الجنوب	2016-03-26 21:19:57	2016-03-26 21:18:46	-1.183333
3	ج	الجنوب	2016-03-26 19:04:57	2016-03-26 19:01:49	-3.133333
4	ج	الجنوب	2016-03-26 16:42:57	2016-03-26 16:42:39	-0.300000

ما هو وقت الحافلات؟

هناك ست مجموعات بيانات في هذا الجدول: اتجاهات الشمال والجنوب لكل مسار C و D و E. للحصول على فكرة عن خصائصها ، دعنا نبني رسم بياني لوقت الوصول الفعلي المخطط له لكل من هذه الستة:

 import seaborn as sns g = sns.FacetGrid(df, row="direction", col="route") g.map(plt.hist, "minutes_late", bins=np.arange(-10, 20)) g.set_titles('{col_name} {row_name}') g.set_axis_labels('minutes late', 'number of buses'); 

من المنطقي أن نفترض أن الحافلات أقرب إلى الجدول الزمني في بداية المسار وتنحرف أكثر عنها في النهاية. تؤكد البيانات هذا: توقفنا على الطريق الجنوبي C ، وكذلك في الشمال D و E قريب من بداية المسار ، وفي الاتجاه المعاكس ، ليس بعيدًا عن الوجهة النهائية.

فترات مجدولة وملاحظة

ألق نظرة على فترات الحافلات المرصودة والمخططة لهذه المسارات الستة. لنبدأ بوظيفة groupby في Pandas لحساب هذه الفواصل الزمنية:

 def compute_headway(scheduled): minute = np.timedelta64(1, 'm') return scheduled.sort_values().diff() / minute grouped = df.groupby(['route', 'direction']) df['actual_interval'] = grouped['actual'].transform(compute_headway) df['scheduled_interval'] = grouped['scheduled'].transform(compute_headway) 

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "actual_interval", bins=np.arange(50) + 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('actual interval (minutes)', 'number of buses'); 

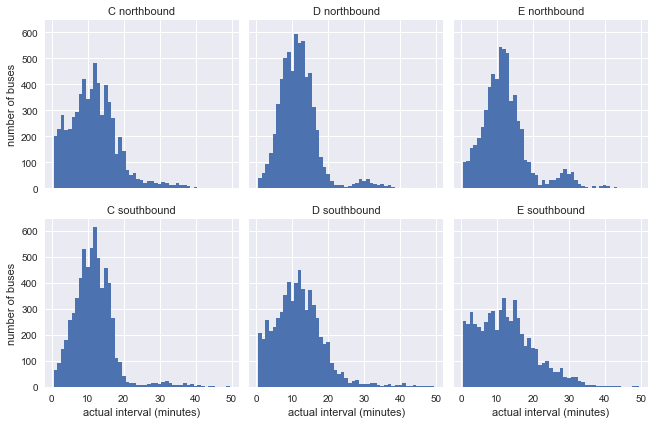
من الواضح بالفعل أن النتائج لا تشبه إلى حد كبير التوزيع الأسي لنموذجنا ، ولكن هذا لا يزال لا يقول أي شيء: يمكن أن تتأثر التوزيعات بفترات غير متناسقة في الرسم البياني.

دعونا نكرر بناء الرسوم البيانية ، مع أخذ فترات الوصول المخطط لها ، وليس فترات الوصول الملحوظة:

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "scheduled_interval", bins=np.arange(20) - 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('scheduled interval (minutes)', 'frequency'); 

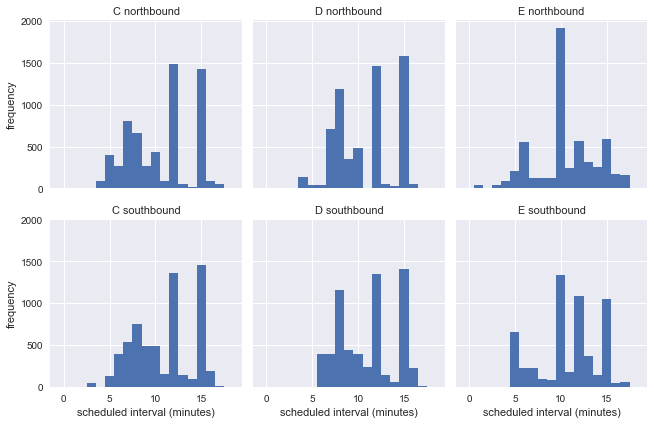
يوضح هذا أنه خلال الأسبوع تعمل الحافلات على فترات مختلفة ، لذلك لا يمكننا تقدير دقة مفارقة وقت الانتظار باستخدام معلومات حقيقية من محطة الحافلات.

بناء جداول موحدة

على الرغم من أن الجدول الرسمي لا يعطي فترات زمنية موحدة ، إلا أن هناك عدة فترات زمنية محددة مع عدد كبير من الحافلات: على سبيل المثال ، ما يقرب من 2000 حافلة من الطريق E إلى الشمال مع فترة مخطط لها مدتها 10 دقائق. لمعرفة ما إذا كانت مفارقة الكمون قابلة للتطبيق ، فلنقم بتجميع البيانات في المسارات والاتجاهات والفاصل الزمني المخطط ، ثم أعد تكديسها كما لو كانت قد حدثت بالتسلسل. يجب أن يحافظ هذا على جميع الخصائص ذات الصلة لبيانات المصدر ، مع تسهيل المقارنة المباشرة مع تنبؤات مفارقة الكمون.

 def stack_sequence(data): # first, sort by scheduled time data = data.sort_values('scheduled') # re-stack data & recompute relevant quantities data['scheduled'] = data['scheduled_interval'].cumsum() data['actual'] = data['scheduled'] + data['minutes_late'] data['actual_interval'] = data['actual'].sort_values().diff() return data subset = df[df.scheduled_interval.isin([10, 12, 15])] grouped = subset.groupby(['route', 'direction', 'scheduled_interval']) sequenced = grouped.apply(stack_sequence).reset_index(drop=True) sequenced.head() 

	الطريق	الاتجاه	الجدول الزمني	حقيقة الوصول	التأخير (دقيقة)	حقيقة الفاصل الزمني	الفاصل الزمني المقرر
0	ج	الشمال	10.0	12.400000	2،400،000	NaN	10.0
1	ج	الشمال	20.0	27.150000	7.150000	0.183333	10.0
2	ج	الشمال	30.0	26.966667	-3.033333	14.566667	10.0
3	ج	الشمال	40.0	35.516667	-4.483333	8.366667	10.0
4	ج	الشمال	50.0	53.583333	3.583333	18.066667	10.0

على البيانات التي تم مسحها ، يمكنك عمل رسم بياني لتوزيع المظهر الفعلي للحافلات على طول كل طريق واتجاه مع تكرار الوصول:

 for route in ['C', 'D', 'E']: g = sns.FacetGrid(sequenced.query(f"route == '{route}'"), row="direction", col="scheduled_interval") g.map(plt.hist, "actual_interval", bins=np.arange(40) + 0.5) g.set_titles('{row_name} ({col_name:.0f} min)') g.set_axis_labels('actual interval (min)', 'count') g.fig.set_size_inches(8, 4) g.fig.suptitle(f'{route} line', y=1.05, fontsize=14) 

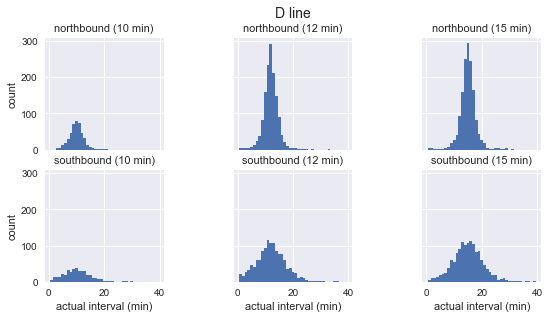
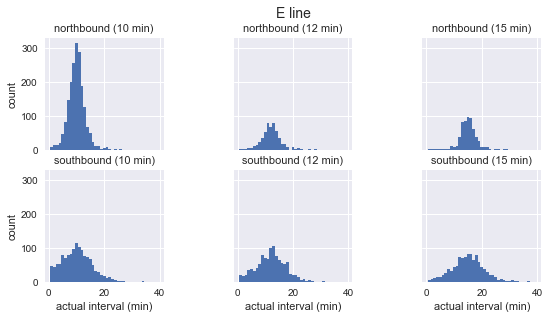
نرى أن توزيع الفترات الزمنية المرصودة لكل مسار تقريبًا هو Gaussian. يبلغ ذروته بالقرب من الفاصل الزمني المخطط وله انحراف معياري أقل في بداية المسار (جنوبًا لـ C ، شمالًا لـ D / E) وأكثر في النهاية. حتى من خلال الرؤية ، لا تتوافق فترات الوصول الفعلية بالتأكيد مع التوزيع الأسي ، وهو الافتراض الرئيسي الذي تستند إليه مفارقة وقت الانتظار.

يمكننا أخذ وظيفة محاكاة وقت الانتظار التي استخدمناها أعلاه للعثور على متوسط ​​وقت الانتظار لكل مسار واتجاه وجدول للحافلات:

 grouped = sequenced.groupby(['route', 'direction', 'scheduled_interval']) sims = grouped['actual'].apply(simulate_wait_times) sims.apply(lambda times: "{0:.1f} +/- {1:.1f}".format(times.mean(), times.std())) 

  الفاصل الزمني المحدد لاتجاه المسار
 C شمال 10.0 7.8 +/- 12.5
                       12.0 7.4 +/- 5.7
                       15.0 8.8 +/- 6.4
          الجنوب 10.0 6.2 +/- 6.3
                       12.0 6.8 +/- 5.2
                       15.0 8.4 +/- 7.3
 D الشمال 10.0 6.1 +/- 7.1
                       12.0 6.5 +/- 4.6
                       15.0 7.9 +/- 5.3
          الجنوب 10.0 6.7 +/- 5.3
                       12.0 7.5 +/- 5.9
                       15.0 8.8 +/- 6.5
 شمالاً 10.0 5.5 +/- 3.7
                       12.0 6.5 +/- 4.3
                       15.0 7.9 +/- 4.9
          الجنوب 10.0 6.8 +/- 5.6
                       12.0 7.3 +/- 5.2
                       15.0 8.7 +/- 6.0
 الاسم: الفعلي ، النوع: الكائن 

متوسط ​​وقت الانتظار ، ربما دقيقة أو دقيقتين ، هو أكثر من نصف الفاصل الزمني المخطط ، ولكنه لا يساوي الفاصل الزمني المخطط ، كما تشير مفارقة وقت الانتظار. بمعنى آخر ، تم تأكيد مفارقة المعاينة ، لكن مفارقة وقت الانتظار غير صحيحة.

الخلاصة

كانت مفارقة الكمون نقطة بداية مثيرة للاهتمام للمناقشة التي تضمنت النمذجة ونظرية الاحتمالات ومقارنة الافتراضات الإحصائية بالواقع. على الرغم من أننا أكدنا أنه في العالم الحقيقي ، تخضع طرق الحافلات لبعض مفارقات التفتيش ، إلا أن التحليل أعلاه يظهر بشكل مقنع تمامًا: الافتراض الرئيسي الكامن وراء مفارقة وقت الانتظار - أن وصول الحافلات يتبع إحصائيات عملية بواسون - ليس له ما يبرره.

في وقت لاحق ، هذا ليس مفاجئًا: عملية بواسون هي عملية بلا ذاكرة تفترض أن احتمال الوصول مستقل تمامًا عن الوقت منذ الوصول السابق. في الواقع ، يحتوي نظام النقل العام المُدار جيدًا على جداول زمنية منظمة بشكل خاص لتجنب هذا السلوك: لا تبدأ الحافلات مساراتها في أوقات عشوائية خلال اليوم ، ولكنها تبدأ وفقًا للجدول الزمني المختار للنقل الأكثر كفاءة للركاب.

الدرس الأكثر أهمية هو توخي الحذر بشأن الافتراضات التي تقوم بها حول أي مهمة لتحليل البيانات. في بعض الأحيان تكون عملية Poisson وصفًا جيدًا لبيانات وقت الوصول. ولكن لمجرد أن أحد أنواع البيانات يبدو وكأنه نوع بيانات آخر لا يعني أن الافتراضات الصالحة لأحدها صالحة بالضرورة للآخر. غالبًا ما تؤدي الافتراضات التي تبدو صحيحة إلى استنتاجات غير صحيحة.