قبل عام ونصف ، نشرت مقالًا بعنوان
"الرياضيات على الأصابع: طرق المربع الأصغر" ، والذي تلقى استجابة لائقة جدًا ، والتي اشتملت ، في جملة أمور ، على أنني اقترحت رسم بومة. حسنًا ، بما أن البومة ، فأنت بحاجة إلى شرحها مرة أخرى. في غضون أسبوع ، حول هذا الموضوع بالضبط ، سأبدأ بإلقاء العديد من المحاضرات لطلاب الجيولوجيا. أغتنم هذه الفرصة ، أقدم هنا النقاط الرئيسية (المعدلة) كمسودة. هدفي الرئيسي ليس إعطاء وصفة جاهزة من كتاب عن الطعام اللذيذ والصحي ، ولكن شرح سبب ذلك وماذا يوجد في القسم المقابل ، لأن الروابط بين أقسام الرياضيات المختلفة هي الأكثر إثارة للاهتمام!
في الوقت الحالي ، أعتزم كسر النص على النحو التالي:
سأذهب إلى المربعات الصغرى قليلاً جانبية ، من خلال مبدأ أقصى احتمال ، ويتطلب الحد الأدنى من التوجه في نظرية الاحتمالات. تم تصميم هذا النص للسنة الثالثة من كلية الجيولوجيا لدينا ، مما يعني (من وجهة نظر المعدات المعنية!) أن يكون طالب المدرسة الثانوية المهتم بالحماس المناسب قادرًا على فهمه.
ما مدى صحة النظير أو هل تؤمن بنظرية التطور؟
سألني ذات يوم عما إذا كنت أؤمن بنظرية التطور. توقف الآن ، فكر في كيفية الرد عليها.

أنا شخصيا فوجئت ، أجد أنني أجدها قابلة للتصديق ، وأن مسألة الإيمان لا تطرح هنا على الإطلاق. النظرية العلمية لا علاقة لها بالإيمان. باختصار ، لا تبني النظرية سوى نموذج للعالم من حولنا ، ولا حاجة للاعتقاد به. علاوة على ذلك ، يتطلب
معيار بوبر نظرية علمية لتكون قادرة على التفنيد. وكذلك يجب أن تمتلك النظرية السليمة ، قبل كل شيء ، قوة تنبؤية. على سبيل المثال ، إذا قمت بتعديل المحاصيل وراثيًا بطريقة تنتج نفسها المبيدات الحشرية ، فمن المنطقي فقط أن تظهر الحشرات المقاومة لها. ومع ذلك ، من غير الواضح إلى حد كبير أن هذه العملية يمكن أن تبطئ من خلال زراعة النباتات العادية جنبًا إلى جنب مع النباتات المعدلة وراثيًا. استنادًا إلى نظرية التطور ، جعلت المحاكاة المقابلة
مثل هذا التنبؤ ، ويبدو أنه تم
تأكيده .
وما علاقة المربعات الصغرى بها؟
كما ذكرت سابقًا ، سأذهب إلى المربعات الصغرى من خلال مبدأ الاحتمالية القصوى. دعونا توضيح بمثال. لنفترض أننا مهتمون بالبيانات المتعلقة بنمو طيور البطريق ، ولكن يمكننا فقط قياس عدد قليل من هذه الطيور الجميلة. من المنطقي جدًا إدخال نموذج توزيع النمو في المهمة - غالبًا ما يكون أمرًا طبيعيًا. يتميز التوزيع الطبيعي بمعلمتين - متوسط القيمة والانحراف المعياري. لكل قيمة ثابتة للمعلمات ، يمكننا حساب احتمالية إنشاء تلك القياسات التي قمنا بها بالضبط. علاوة على ذلك ، من خلال تغيير المعلمات ، نجد تلك التي تزيد من الاحتمال.
وبالتالي ، للعمل بأقصى قدر من الاحتمالية ، نحتاج إلى العمل من حيث نظرية الاحتمالات. أقل قليلاً ، على الأصابع ، نحدد مفهوم الاحتمال والاحتمال ، ولكن أولاً أود أن أركز على جانب آخر. نادرا ما أرى الناس يفكرون في كلمة "نظرية" في عبارة "نظرية الاحتمالات".
ما هو تعلم المنظر؟
فيما يتعلق بأصول ومعاني ونطاق تقديرات الاحتمالات ، استمر الجدل العنيف لأكثر من مائة عام. على سبيل المثال ، ذكر
برونو دي فينيتي أن الاحتمال ليس أكثر من تحليل شخصي لاحتمال حدوث شيء ما ، وأن هذا الاحتمال غير موجود خارج العقل. هذا هو استعداد الشخص للمراهنة على شيء ما يحدث. يتعارض هذا الرأي مباشرة مع وجهة نظر
كلاسيكيات / freventists حول احتمال نتيجة معينة لحدث ما ، حيث يُفترض أنه يمكن تكرار نفس الحدث عدة مرات ، ويرتبط "احتمال" نتيجة معينة بتكرار نتيجة معينة تقع أثناء الاختبارات المتكررة. بالإضافة إلى الذاتيين والفرنفيين ، هناك أيضًا موضوعيون يجادلون بأن الاحتمالات هي جوانب حقيقية للكون ، وليست مجرد أوصاف لدرجة ثقة المراقب.
كن على هذا النحو ، لكن جميع المدارس العلمية الثلاث في الممارسة تستخدم نفس الجهاز بناءً على بديهيات كولموجوروف. دعونا نقدم حجة غير مباشرة ، من وجهة نظر ذاتية ، لصالح نظرية الاحتمالات ، مبنية على بديهيات كولموجوروف. نعطي البديهيات بأنفسهم بعد ذلك بقليل ، ولكن كبداية سنفترض أن لدينا وكيل مراهنات يقبل الرهانات في كأس العالم المقبلة. دعونا نحصل على حدثين: أ = فريق أوروجواي سيصبح البطل ، ب = الفريق الألماني سيصبح البطل. تقدر شركة المراهنات فرص فريق أوروغواي للفوز بنسبة 40٪ ، وفرص المنتخب الألماني بنسبة 30٪. من الواضح أن ألمانيا وأوروجواي لا يمكنهما الفوز في نفس الوقت ، وبالتالي فإن فرصة a∧b هي صفر. حسنًا ، في الوقت نفسه ، تعتقد شركة المراهنات أن احتمال فوز أوروجواي أو ألمانيا (وليس الأرجنتين أو أستراليا) هو 80٪. لنكتبها بالشكل التالي:

إذا ادعت شركة المراهنات أن درجة ثقته في الحدث
a هي 0.4 ، أي
P (a) = 0.4 ، فيمكن للاعب اختيار ما إذا كان سيراهن على أو ضد قول
أ ، مبالغ مراهنة تتوافق مع درجة ثقة شركة المراهنات. هذا يعني أن اللاعب يمكن أن يراهن على أن الحدث سيحدث عن طريق المراهنة على أربعة روبل مقابل ستة روبل من شركة المراهنات. أو يمكن للاعب المراهنة على ستة روبل بدلاً من أربعة روبل من شركة مراهنات بأن الحدث لن يحدث.
إذا كانت درجة ثقة شركة المراهنات لا تعكس حالة العالم بدقة ، فيمكننا الاعتماد على حقيقة أنها ستخسر على المدى الطويل أموالًا للاعبين الذين تكون معتقداتهم أكثر دقة. علاوة على ذلك ، في هذا المثال بالذات ، لدى اللاعب استراتيجية تخسر فيها شركة المراهنات المال
دائمًا . دعونا نوضح ذلك:

يقوم اللاعب بثلاث رهانات ، ومهما كانت نتيجة البطولة ، فهو يفوز دائمًا. يرجى ملاحظة أن النظر في المكاسب من حيث المبدأ لا يشمل ما إذا كانت أوروغواي أو ألمانيا هي المفضلة للبطولة ، فإن خسارة المراهنات مضمونة! كان هذا الموقف مدفوعًا بحقيقة أن شركة المراهنات لم تسترشد بأساسيات نظرية الاحتمالات ، بعد أن انتهكت بديهية كولموجوروف الثالثة ، فلنجلب لهم الثلاثة:
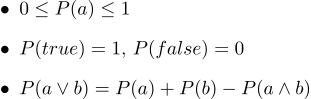
في شكل نص ، تبدو كما يلي:
- 1. تتراوح جميع الاحتمالات من 0 إلى 1
- 2. بالطبع ، البيانات الحقيقية لها احتمال 1 ، وبالتأكيد احتمال خاطئ من 0.
- 3. البديهية الثالثة هي بديهية الانفصال ، من السهل أن نفهمها بشكل بديهي ، مع ملاحظة أن الحالات التي تكون فيها العبارة a صحيحة ، جنبًا إلى جنب مع الحالات التي تكون فيها b صحيحة ، تغطي بالتأكيد جميع الحالات التي تكون فيها العبارة a∨b صحيحة ؛ ولكن في مجموع مجموعتين من الحالات ، يحدث تقاطعهما مرتين ، لذلك ، من الضروري طرح P (a∧b).
في عام 1931 ،
أثبت دي فينيتي بيانًا قويًا جدًا:
إذا كانت شركة المراهنات تسترشد بدرجات عديدة من الثقة ، والتي تنتهك بديهيات نظرية الاحتمالات ، فهناك مجموعة من رهانات اللاعب التي تضمن خسارة المراهنة (يفوز اللاعب) في كل رهان.
يمكن اعتبار بديهيات الاحتمالات على أنها تحد من مجموعة المعتقدات الاحتمالية التي يمكن لبعض العوامل الاحتفاظ بها. يرجى ملاحظة أن اتباع شركة المراهنات لا يعني ضمنًا بديهيات كولموجوروف بأنه سيفوز (سنترك مشكلات العمولة جانبًا) ، ولكن إذا لم تتبعها ، فسيكون مضمونًا أن يخسر. لاحظ أنه تم طرح حجج أخرى لصالح تطبيق الاحتمالات. ولكن كان النجاح
العملي لأنظمة الاستدلال المبنية على نظرية الاحتمالية هو الحافز الجذاب الذي تسبب في مراجعة العديد من وجهات النظر.
لذا ، قمنا بفتح الحجاب بشكل طفيف
لماذا قد يكون للمنظور معنى ، ولكن ما هو نوع الأشياء التي يتلاعب بها؟ النظرية بأكملها مبنية على ثلاث بديهيات فقط. تتضمن الثلاثة بعض الوظائف السحرية
P. علاوة على ذلك ، بالنظر إلى هذه البديهيات ، فإنه يذكرني كثيرًا بوظيفة منطقة الشكل. دعنا نحاول معرفة ما إذا كانت المنطقة تعمل لتحديد الاحتمالية.
نحدد كلمة "حدث" بأنها "مجموعة فرعية من مربع الوحدة". نحدد كلمة "احتمال حدث" على أنها "منطقة المجموعة الفرعية المقابلة". تقريبًا ، لدينا هدف كبير من الورق المقوى ، وقد أغلقنا أعيننا ، بعد أن أغلقنا أعيننا. تتناسب احتمالات سقوط رصاصة في مجموعة معينة بشكل مباشر مع منطقة المجموعة. الحدث الموثوق في هذه الحالة هو المربع بالكامل ، ومن الواضح أنه خطأ ، على سبيل المثال ، أي نقطة من المربع. ويترتب على تعريفنا للاحتمال أنه من المستحيل الوصول إلى النقطة بشكل مثالي (نقطتنا هي نقطة مادية). أنا أحب الصور حقًا ، وأرسم الكثير منها ، والمنظور ليس استثناءً! دعونا نوضح البديهيات الثلاثة:
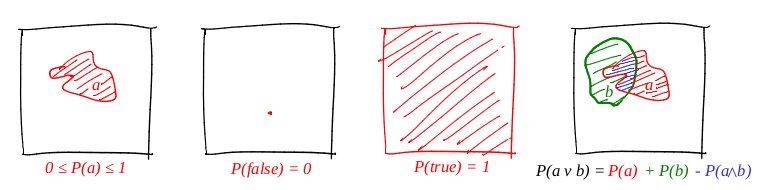
لذلك ، تتحقق البديهية الأولى: المنطقة غير سالبة ولا يمكن أن تتجاوز الوحدات. الحدث الموثوق هو المربع بأكمله ، والخطأ المتعمد هو أي مجموعة من مساحة الصفر. ويعمل بشكل مثالي مع الفصل!
المصداقية القصوى مع أمثلة
مثال واحد: Coin Flip
دعونا نلقي نظرة على أبسط مثال على رمي العملة ، ويعرف أيضًا
بمخطط برنولي . يتم إجراء تجارب
N ، في كل منها يمكن أن يحدث فيها أحد الحدثين ("النجاح" أو "الفشل") ، أحدهما مع الاحتمال
p ، والثاني مع الاحتمال
1-p . مهمتنا هي العثور على احتمالية الحصول على نجاحات
k بالضبط في هذه التجارب. يعطينا هذا الاحتمال صيغة برنولي:
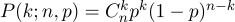
خذ عملة عادية (
p = 0.5 ) ، ارمها عشر مرات (
n = 10 ) ، وفكر في عدد المرات التي يتم فيها إسقاط ذيول:
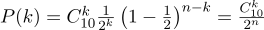
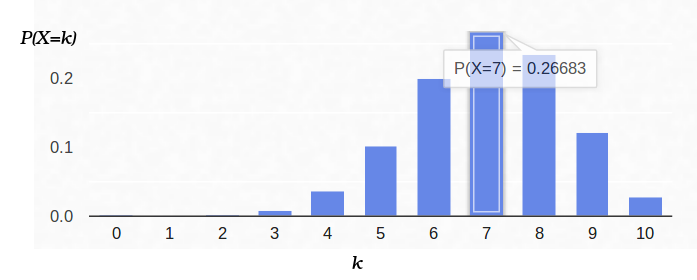
فيما يلي رسم بياني لكثافة الاحتمال:
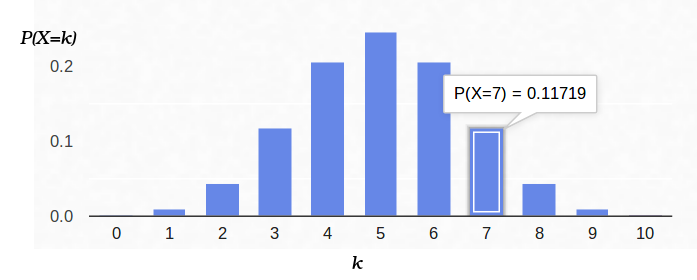
وبالتالي ، إذا حددنا احتمالية ظهور "النجاح" (0.5) ، وسجلنا أيضًا عدد التجارب (10) ، فإن العدد المحتمل لـ "النجاحات" يمكن أن يكون أي عدد صحيح بين 0 و 10 ، ومع ذلك ، فإن هذه النتائج ليست محتملة بنفس القدر. من الواضح أن الحصول على خمسة "نجاحات" أكثر ترجيحًا من عدم تحقيقها. على سبيل المثال ، يبلغ احتمال عد سبعة ذيول حوالي 12٪.
الآن دعونا نلقي نظرة على نفس المهمة من الجانب الآخر. لدينا عملة حقيقية ، لكننا لا نعرف توزيعها لاحتمال مسبق "النجاح" / "الفشل". ومع ذلك ، يمكننا رميها عشر مرات وحساب عدد "النجاحات". على سبيل المثال ، لدينا سبعة ذيول. كيف يساعدنا ذلك في تقييم
p ؟
يمكننا محاولة إصلاح
n = 10 و
k = 7 في صيغة برنولي ، مع ترك
p معلمة مجانية:

ثم يمكن تفسير صيغة برنولي على أنها
احتمال المعلمة المقدرة ، (في هذه الحالة ،
ص ). حتى أنني غيرت حرف الوظيفة ، الآن هو
L (من شبه اللغة الإنجليزية). أي أن الاحتمال هو احتمال توليد بيانات المراقبة (7 ذيول من 10 تجارب) لقيمة معينة من المعلمات (المعلمات).
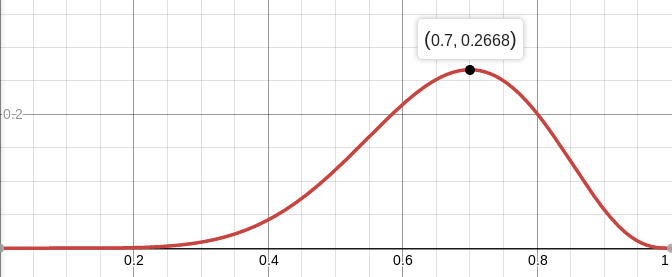
على سبيل المثال ، احتمالية وجود عملة متوازنة (
p = 0.5) ، بشرط أن تحدث سبعة ذيول من كل عشرة رميات ، تبلغ حوالي 12 ٪. يمكنك رسم الدالة
L :
لذلك ، نحن نبحث عن قيمة المعلمات التي تزيد من احتمالية الحصول على تلك الملاحظات التي لدينا. في هذه الحالة بالذات ، لدينا وظيفة متغير واحد ، ونحن نبحث عن الحد الأقصى. لتسهيل البحث ، سأبحث عن حد أقصى ليس
L ، ولكن
سجل L. اللوغاريتم هو وظيفة رتيبة تمامًا ، لذا فإن تعظيم أحدهما والآخر هو نفس الشيء تمامًا. ويقسم اللوغاريتم المنتج إلى مبلغ أكثر ملاءمة للتمييز. لذلك ، نحن نبحث عن الحد الأقصى لهذه الوظيفة:

للقيام بذلك ، نساوي مشتقها بالصفر:
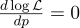
مشتق log x = 1 / x نحصل على:

أي أنه تم الوصول إلى أقصى احتمال (حوالي 27٪) عند

فقط في حالة احتساب المشتق الثاني:
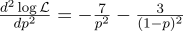
عند النقطة p = 0.7 ، تكون سالبة ، لذا فإن هذه النقطة هي في الواقع الحد الأقصى للدالة L.
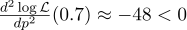
وهنا كثافة الاحتمال لمخطط برنولي مع
p = 0.7:
المثال الثاني: ADC
دعونا نتخيل أن لدينا كمية مادية ثابتة معينة نريد قياسها ، سواء كان ذلك بطول مسطرة أو جهد بمقياس الفولتميتر. يعطي أي قياس
تقريبًا لهذه الكمية ، ولكن ليس الكمية نفسها. طور غاوس الطرق التي أصفها هنا في نهاية القرن الثامن عشر ، عندما قام بقياس مدارات الأجرام السماوية.
على سبيل المثال ، إذا قمنا بقياس جهد البطارية N مرة ، نحصل على N قياسات مختلفة. أيهما تأخذ؟ هذا كل شيء! لذا ، دعونا نحصل على كميات N Uj:
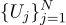
افترض أن كل قياس Uj يساوي قيمة مثالية ، بالإضافة إلى الضوضاء الغوسية ، التي تتميز بمعلمتين - موضع الجرس الغوسي و "عرضه". إليك كثافة الاحتمال:
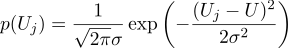
بمعنى ، بعد أن تم إعطاء N قيم Uj ، فإن مهمتنا هي العثور على هذه المعلمة ، U التي تزيد من قيمة الاحتمال. يمكن كتابة المصداقية (آخذ اللوغاريتم منها على الفور) على النحو التالي:
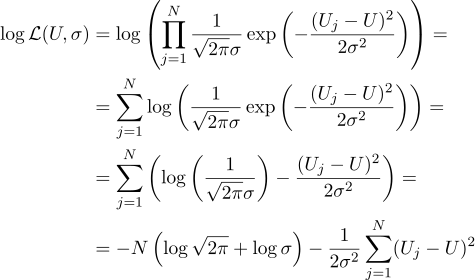
حسنًا ، كل شيء صار تمامًا كما كان من قبل ، فنحن نساوي صفر مشتقات جزئية فيما يتعلق بالمعايير التي نبحث عنها:
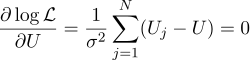
نجد أن أكثر تقدير محتمل للكمية غير المعروفة U يمكن العثور عليه كمتوسط لجميع القياسات:
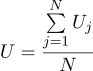
حسنًا ، أكثر معلمات سيجما على الأرجح هي الانحراف المعياري المعتاد:
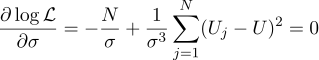

هل كان الأمر يستحق الإزعاج للحصول على متوسط بسيط لجميع القياسات في الإجابة؟ لذوقي ، كان يستحق ذلك. بالمناسبة ، يعد قياس قياسات متعددة لقيمة ثابتة من أجل زيادة دقة القياسات ممارسة قياسية. على سبيل المثال ،
متوسط ADC . بالمناسبة ، لأن هذا الضجيج الغوسي ليس ضروريًا ، يكفي أن يكون الضجيج غير متحيز.
المثال الثالث ، ومرة أخرى أحادية البعد
نواصل المحادثة ، لنأخذ نفس المثال ، لكن نعقده قليلاً. نريد قياس مقاومة مقاوم معين. بمساعدة مصدر طاقة المختبر ، يمكننا تمرير عدد قياسي من الأمبير من خلاله ، وقياس الجهد المطلوب لذلك. أي ، سيكون لدينا أزواج N من الأرقام (Ij ، Uj) عند مدخلات مقيم المقاومة لدينا.
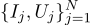
ارسم هذه النقاط على الرسم البياني ؛ يخبرنا قانون أوم أننا نبحث عن منحدر الخط الأزرق.
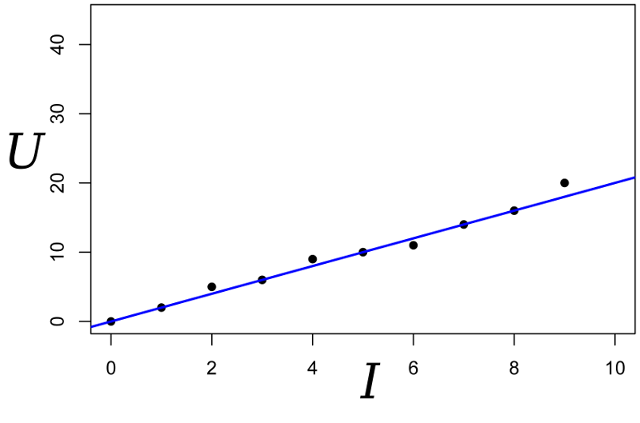
نكتب التعبير لاحتمالية المعلمة R:
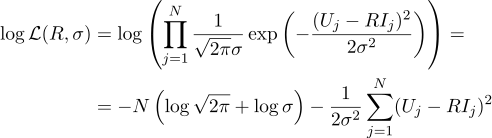
ومرة أخرى ، نعادل الصفر بالمشتق الجزئي المقابل:
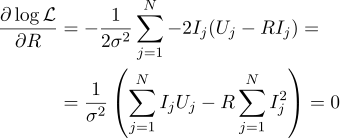
ثم يمكن العثور على المقاومة الأكثر معقولية R بالصيغة التالية:
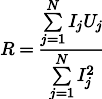
هذه النتيجة بالفعل أقل وضوحًا إلى حد ما من المتوسط البسيط لجميع القياسات. يرجى ملاحظة أنه إذا أخذنا مائة قياس في منطقة أمبير واحد ، وقياس واحد في منطقة كيلو أمبير ، فإن القياسات المائة السابقة لن تؤثر عمليًا على النتيجة. لنتذكر هذه الحقيقة ، ستكون مفيدة لنا في المقالة القادمة.
المثال الرابع: العودة إلى المربعات الصغرى
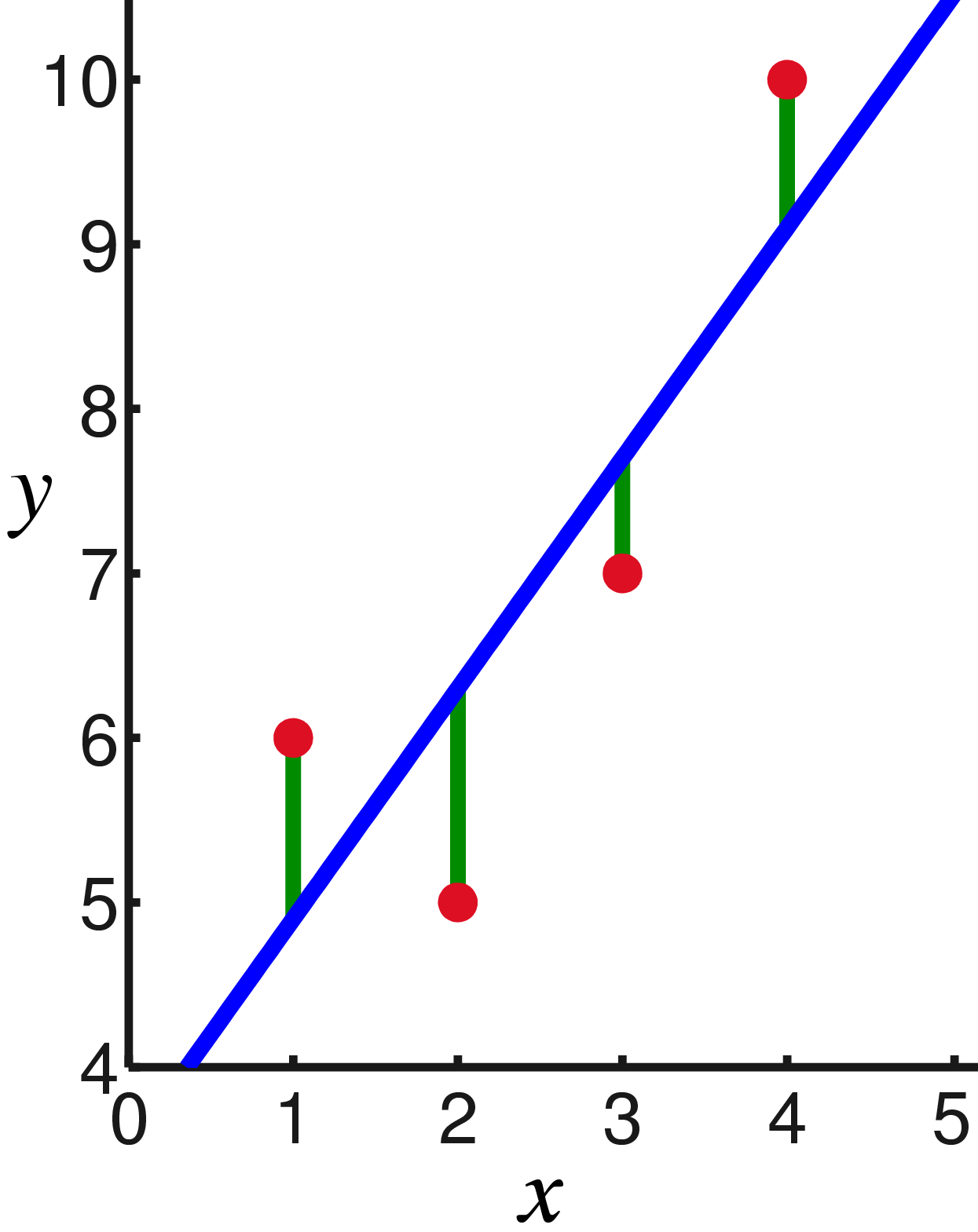
من المؤكد أنك قد لاحظت بالفعل أنه في المثالين الأخيرين ، فإن تعظيم لوغاريتم الاحتمالية يعادل تقليل مجموع مربعات خطأ التقدير. دعونا نلقي نظرة على مثال آخر. قم بمعايرة القياسات باستخدام الأوزان المرجعية. لنفترض أن لدينا N أحمالًا مرجعية من الكتلة xj ، وعلقها على steelyard وقياس طول الزنبرك ، نحصل على N من أطوال الربيع yj:

يخبرنا قانون هوكي أن تمديد النابض يعتمد خطيًا على القوة المطبقة ، وتشمل هذه القوة وزن البضائع ووزن النابض نفسه. دع صلابة الربيع تكون المعلمة
a ، لكن توتر الربيع تحت وزنه هو المعلمة b. ثم يمكننا كتابة التعبير عن احتمالية قياساتنا بهذه الطريقة (كما كان من قبل ، تحت فرضية ضوضاء قياس غاوس):
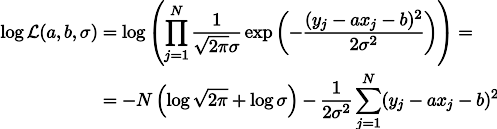
إن تعظيم احتمالية L يساوي تقليل مجموع مربعات أخطاء التقدير ، أي يمكننا البحث عن الحد الأدنى من الدالة S المحددة على النحو التالي:
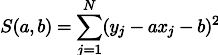
بعبارة أخرى ، نحن نبحث عن خط مستقيم يقلل من مجموع مربعات أطوال المقاطع الخضراء:
حسنًا ، إذن لا مفاجآت ، وضعنا مشتقات جزئية على الصفر:
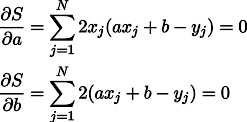
نحصل على نظام من معادلتين خطيتين مع مجهولين:
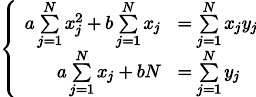
نتذكر الصف السابع من المدرسة ونكتب الحل:

الخلاصة
تعد الطرق المربعة الصغرى حالة خاصة لزيادة احتمالية تلك الحالات حيث تكون كثافة الاحتمال غوسية. في الحالة التي تكون فيها الكثافة (على الإطلاق) غوسية ، تعطي المربعات الأقل تقديرًا يختلف عن MLE (الحد الأقصى لتقدير التشابه). بالمناسبة ، في وقت واحد ، افترض غاوس أن التوزيع لا يلعب دورًا ، فقط استقلالية الاختبارات مهمة.
كما ترون من هذه المقالة ، كلما كانت الغابة أبعد ، كلما كانت الحلول التحليلية لهذه المشكلة أكثر تعقيدًا. , ! , , , .