لقد حضرت لفترة طويلة وجمعت المواد ، آمل أن تكون هذه المرة أفضل. أكرس هذه المقالة للطرق الأساسية لحل مشاكل التحسين الرياضي مع قيود ، لذلك إذا سمعت أن طريقة simplex هي طريقة
مهمة جدًا ، ولكنك لا تزال لا تعرف ما تفعله ، فمن المحتمل أن تساعدك هذه المقالة.
ملاحظة: تحتوي المقالة على صيغ رياضية يضيفها محرر الماكرو. يقولون أنه في بعض الأحيان لا يتم عرضها. هناك أيضًا العديد من الرسوم المتحركة بتنسيق gif.
الديباجة
مشكلة التحسين الرياضي هي مشكلة النموذج "بحث في المجموعة
mathcalK العنصر
x∗ مثل هذا للجميع
x من
mathcalK نفذت
f(x∗) leqf(x) "، والذي من المرجح أن يكتب في الأدبيات العلمية شيء من هذا القبيل
\ start {array} {rl} \ mbox {minimize} & f (x) \\ \ mbox {provided} & x \ in \ mathcal {K}. \ end {array}
\ start {array} {rl} \ mbox {minimize} & f (x) \\ \ mbox {provided} & x \ in \ mathcal {K}. \ end {array}
تاريخيًا ، لا تعمل الطرق الشائعة مثل أصل التدرج أو طريقة نيوتن إلا في المساحات الخطية (ويفضل أن تكون بسيطة ، على سبيل المثال
mathbbRn ) في الممارسة العملية ، غالبًا ما تكون هناك مشاكل حيث تحتاج إلى إيجاد الحد الأدنى ليس في الفضاء الخطي. على سبيل المثال ، تحتاج إلى العثور على الحد الأدنى من بعض الوظائف على هذه المتجهات
x=(x1، ldots،xn) من أجله
xi geq0 ، قد يكون هذا يرجع إلى حقيقة ذلك
xi تشير إلى أطوال أي كائنات. أو على سبيل المثال ، إذا
x تمثل إحداثيات نقطة يجب ألا تزيد عن
r من
y أي
|x−y | leqr . لمثل هذه المشاكل ، لم يعد الانحدار التدريجي أو طريقة نيوتن قابلة للتطبيق بشكل مباشر. اتضح أن فئة كبيرة جدًا من مشكلات التحسين تمت تغطيتها بشكل ملائم من خلال "القيود" ، على غرار تلك التي وصفتها أعلاه. بعبارة أخرى ، من الملائم تمثيل المجموعة
mathcalK في شكل نظام من المساواة والمساواة
startarraylgi(x) leq0، 1 leqi leqm،hi(x)=0، 1 leqi leqk. endarray
مشاكل التقليل عبر مساحة من النموذج
mathbbRn وهكذا بدأوا في تسميتها بشكل تعسفي بـ "مشكلة غير مقيدة" ، ومشاكل حول مجموعات محددة بمجموعات من المساواة وعدم المساواة - "مشاكل مقيدة".
من الناحية الفنية ، على الإطلاق أي عدد
mathcalK يمكن تمثيلها كمساواة واحدة أو عدم مساواة باستخدام وظيفة
المؤشر ، والتي يتم تعريفها على أنها
I_ \ mathcal {K} (x) = \ start {cases} 0 ، و x \ notin \ mathcal {K} \\ 1 ، & x \ in \ mathcal {K} ، \ end {cases}
I_ \ mathcal {K} (x) = \ start {cases} 0 ، و x \ notin \ mathcal {K} \\ 1 ، & x \ in \ mathcal {K} ، \ end {cases}
ومع ذلك ، فإن هذه الوظيفة لا تحتوي على خصائص مفيدة مختلفة (محدبة ، تفاضلية ، إلخ). ومع ذلك ، يمكن للمرء أن يتصور في كثير من الأحيان
mathcalK في شكل عدة مساواة وعدم مساواة ، لكل منها مثل هذه الخصائص. يتم تلخيص النظرية الأساسية تحت القضية
\ start {array} {rl} \ mbox {minimize} & f (x) \\ \ mbox {provided} & g_i (x) \ leq 0، ~ 1 \ leq i \ leq m \\ & Ax = b ، \ end {array}
\ start {array} {rl} \ mbox {minimize} & f (x) \\ \ mbox {provided} & g_i (x) \ leq 0، ~ 1 \ leq i \ leq m \\ & Ax = b ، \ end {array}
أين
f،gi - وظائف محدبة (ولكن ليست بالضرورة قابلة للتمييز) ،
A - مصفوفة. لتوضيح كيفية عمل الأساليب ، سأستخدم مثالين:
- مهمة البرمجة الخطية
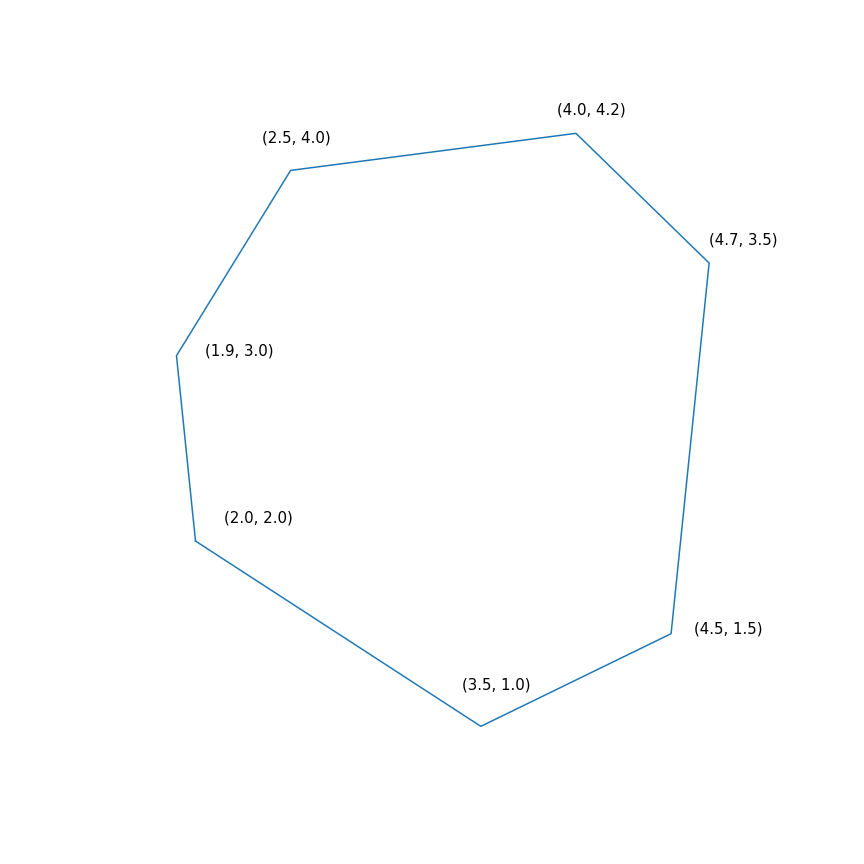
$$ display $$ \ start {array} {rl} \ mbox {minimize} & -2 & x ~~~ - & y \\ \ mbox {provided} & -1.0 & ~ x -0.1 & ~ y \ leq -1.0 \ \ & -1.0 & ~ x + ~ 0.6 & ~ y \ leq -1.0 \\ & -0.2 & ~ x + ~ 1.5 & ~ y \ leq -0.2 \\ & ~ 0.7 & ~ x + ~ 0.7 & ~ y \ leq 0.7 \\ & ~ 2.0 & ~ x -0.2 & ~ y \ leq 2.0 \\ & ~ 0.5 & ~ x -1.0 & ~ y \ leq 0.5 \\ & -1.0 & ~ x -1.5 & ~ y \ leq - 1.0 \\ \ end {array} $$ display $$
في جوهرها ، تتكون هذه المشكلة في العثور على أبعد نقطة للمضلع في الاتجاه (2 ، 1) ، وحل المشكلة هو النقطة (4.7 ، 3.5) - "الأكثر" حقًا في المضلع. لكن المضلع نفسه
- تصغير دالة تربيعية بقيد تربيعي واحد
\ start {array} {rl} \ mbox {minimize} & 0.7 (x - y) ^ 2 + 0.1 (x + y) ^ 2 \\ \ mbox {provided} & (x-4) ^ 2 + ( ص -6) ^ 2 \ leq 9 \ end {array}
\ start {array} {rl} \ mbox {minimize} & 0.7 (x - y) ^ 2 + 0.1 (x + y) ^ 2 \\ \ mbox {provided} & (x-4) ^ 2 + ( ص -6) ^ 2 \ leq 9 \ end {array}
طريقة البسيط
من بين جميع الطرق التي أغطيها في هذه المراجعة ، ربما تكون الطريقة البسيطة هي الأكثر شهرة. تم تطوير الطريقة خصيصًا للبرمجة الخطية والواحدة فقط من المقدمة تقدم الحل الدقيق في عدد محدود من الخطوات (شريطة أن يتم استخدام الحساب الدقيق للحسابات ، عمليًا لا يكون هذا هو الحال ، ولكن من الناحية النظرية يكون ذلك ممكنًا). تتكون فكرة الطريقة البسيطة من جزأين:
- تحدد أنظمة التفاوتات والمساواة الخطية متعددة الوجوه محدبة الأبعاد (polytopes). في الحالة أحادية البعد ، هذه نقطة أو شعاع أو مقطع ، في الحالة ثنائية الأبعاد ، مضلع محدب ، في الحالة ثلاثية الأبعاد ، محدب متعدد الوجوه. تقليل الدالة الخطية هو في الأساس العثور على النقطة "الأبعد" في اتجاه معين. أعتقد أن الحدس يجب أن يشير إلى أن هذه النقطة البعيدة جدًا يجب أن تكون ذروة معينة ، وهذا هو الحال بالفعل. بشكل عام ، لنظام من م عدم المساواة في n -البعد البعد الرأس هو نقطة ترضي نظامًا بالضبط n تتحول أوجه عدم المساواة هذه إلى مساواة (شريطة عدم وجود معادلات بين أوجه عدم المساواة). هناك دائمًا عدد محدود من هذه النقاط ، على الرغم من أنه يمكن أن يكون هناك الكثير منها.
- الآن لدينا مجموعة محدودة من النقاط ، بشكل عام ، يمكنك ببساطة اختيارها وتصنيفها ، أي القيام بشيء من هذا القبيل: لكل مجموعة فرعية من n عدم المساواة ، حل نظام المعادلات الخطية التي تم تجميعها على عدم المساواة المختارة ، والتحقق من أن الحل يناسب النظام الأصلي لعدم المساواة والمقارنة مع هذه النقاط الأخرى. هذه طريقة بسيطة إلى حد ما ولكنها غير فعالة. طريقة البسيط ، بدلاً من التكرار ، تنتقل من الأعلى إلى الأعلى على طول الحواف بحيث تتحسن قيم دالة الهدف. اتضح أنه إذا لم يكن لدى الرأس "جيران" تكون فيها قيم الوظيفة أفضل ، فهي مثالية.
طريقة simplex تكرارية ، أي أنها تحسن بشكل تسلسلي المحلول قليلاً. لمثل هذه الأساليب ، تحتاج إلى البدء من مكان ما ، في الحالة العامة يتم ذلك عن طريق حل مشكلة مساعدة
\ start {array} {rl} \ mbox {minimize} & s \\ \ mbox {provided} & g_i (x) \ leq s، ~ 1 \ leq i \ leq m \\ \ end {array}
\ start {array} {rl} \ mbox {minimize} & s \\ \ mbox {provided} & g_i (x) \ leq s، ~ 1 \ leq i \ leq m \\ \ end {array}
إذا لحل هذه المشكلة
x∗،s∗ مثل هذا
s∗ leq0 ثم أعدم
gi(x∗) leqs leq0 خلاف ذلك ، عادة ما يتم إعطاء المشكلة الأصلية على مجموعة فارغة. لحل المشكلة المساعدة ، يمكنك أيضًا استخدام طريقة simplex ، ولكن يمكن أخذ نقطة البداية
s= maxigi(x) مع التعسفي
x . يمكن أن يسمى العثور على نقطة البداية بشكل تعسفي المرحلة الأولى من الطريقة ، وإيجاد حل للمشكلة الأصلية يمكن أن يسمى بشكل تعسفي المرحلة الثانية من الطريقة.
مسار الطريقة البسيطة على مرحلتينتم إنشاء المسار باستخدام scipy.optimize.linprog.
أصل التدرج الإسقاطي
حول أصل التدرج ، كتبت مؤخرًا مقالة منفصلة وصفت فيها بإيجاز هذه الطريقة. الآن هذه الطريقة حية للغاية ، ولكن يتم دراستها كجزء من
نزول التدرج الداني الأكثر عمومية. فكرة هذه الطريقة مبتذلة تمامًا: إذا طبقنا نزول التدرج على دالة محدبة
f ، مع الاختيار الصحيح للمعلمات نحصل على الحد الأدنى العالمي
f . إذا ، بعد كل خطوة من نزول التدرج ، يتم تصحيح النقطة التي تم الحصول عليها ، بدلاً من ذلك إسقاطها على مجموعة محدبة مغلقة
mathcalK ، ونتيجة لذلك نحصل على الحد الأدنى من الوظيفة
f على
mathcalK . حسنًا ، أو بشكل أكثر رسمية ، يكون نزول التدرج الإسقاطي خوارزمية يتم حسابها بالتسلسل
startcasesxk+1=yk− alphak nablaf(yk)yk+1=P mathcalK(xk+1)، نهايةالحالات
أين
P mathcalK(x)= mboxargminy in mathcalK |x−y |.
تحدد المساواة الأخيرة عامل التشغيل القياسي للإسقاط على المجموعة ؛ في الواقع ، إنها وظيفة
x تحسب أقرب نقطة للمجموعة
mathcalK . يلعب دور المسافة هنا
| ldots | ، تجدر الإشارة إلى أنه يمكن استخدام أي
معيار هنا ، ومع ذلك ، قد تختلف الإسقاطات بمعايير مختلفة!
من الناحية العملية ، يتم استخدام أصل التدرج الإسقاطي فقط في حالات خاصة. مشكلتها الرئيسية هي أن حساب الإسقاط يمكن أن يكون أكثر صعوبة من العرض الأصلي ، ويجب حسابه عدة مرات. الحالة الأكثر شيوعًا التي يكون مناسبًا لاستخدامها في التدرج الإسقاطي التدريجي هي "قيود الصندوق" ، التي لها الشكل
elli leqxi leqri، 1 leqi leqn.
في هذه الحالة ، يتم حساب الإسقاط بكل بساطة ، حيث يتحول كل إحداثي
[P _ {\ mathcal {K}} (x)] _ i = \ start {cases} r_i، & x_i> r_i \\ \ ell_i، & x_i <\ ell_i \\ x_i، & x_i \ in [\ ell_i، r_i ]. \ end {cases}
[P _ {\ mathcal {K}} (x)] _ i = \ start {cases} r_i، & x_i> r_i \\ \ ell_i، & x_i <\ ell_i \\ x_i، & x_i \ in [\ ell_i، r_i ]. \ end {cases}
استخدام أصل التدرج الإسقاطي لمشاكل البرمجة الخطية لا معنى له على الإطلاق ، ومع ذلك ، إذا قمت بذلك ، فسيبدو شيئًا مثل هذا
مسار نزول التدرج الإسقاطي لمشكلة البرمجة الخطية وهنا مسار نزول التدرج الإسقاطي للمشكلة الثانية ، إذا
وإذا
طريقة القطع الناقص
وتجدر الإشارة إلى أن هذه الطريقة هي أول خوارزمية متعددة الحدود لمشاكل البرمجة الخطية ، ويمكن اعتبارها تعميماً متعدد الأبعاد
لطريقة التقطيع . سأبدأ بطريقة أكثر عمومية
لفصل سطح الطائرة :
- في كل خطوة من الطريقة ، هناك مجموعة تحتوي على حل المشكلة.
- في كل خطوة ، يتم إنشاء الطائرة الزائدة ، وبعد ذلك تتم إزالة جميع النقاط الموجودة على جانب واحد من الطائرة الزائدة المحددة من المجموعة ، ويمكن إضافة بعض النقاط الجديدة إلى هذه المجموعة
بالنسبة لمشكلات التحسين ، يستند بناء "الفصل الزائد" إلى عدم المساواة التالي لوظائف محدبة
f(y) geqf(x)+ nablaf(x)T(y−x).
إذا تم الإصلاح
x ثم لدالة محدبة
f نصف مساحة
nablaf(x)T(y−x) geq0 يحتوي فقط على نقاط بقيمة لا تقل عن نقطة
x ، مما يعني أنه يمكن قطعها ، لأن هذه النقاط ليست أفضل من تلك التي وجدناها بالفعل. بالنسبة للمشكلات المتعلقة بالقيود ، يمكنك بالمثل التخلص من النقاط المضمونة بانتهاك أحد القيود.
إن أبسط نسخة من طريقة الفصل المفرط هي ببساطة قطع نصف المسافات دون إضافة أي نقاط. ونتيجة لذلك ، سيكون لدينا في كل خطوة وجود متعدد الوجوه. المشكلة في هذه الطريقة هي أن عدد وجوه متعدد الوجوه من المرجح أن يزداد من خطوة إلى خطوة. علاوة على ذلك ، يمكن أن تنمو بشكل كبير.
تخزن طريقة القطع الناقص فعليًا القطع الناقص في كل خطوة. بتعبير أدق ، بعد بناء الطائرة الزائدة ، يتم بناء القطع الناقص من الحجم الأدنى ، والذي يحتوي على أحد أجزاء النص الأصلي. يمكن تحقيق ذلك بإضافة نقاط جديدة. يمكن دائمًا تحديد القطع الناقص بواسطة مصفوفة محددة موجبة ومتجه (مركز القطع الناقص) على النحو التالي
\ mathcal {E} (P، x) = \ {z ~ | ~ (z-x) ^ TP (z-x) \ leq 1 \}.
\ mathcal {E} (P، x) = \ {z ~ | ~ (z-x) ^ TP (z-x) \ leq 1 \}.
يمكن أن يتم بناء الحد الأدنى من حجم القطع الناقص ، الذي يحتوي على تقاطع نصف مساحة وبيضاوي آخر ، باستخدام
صيغ معقدة مرهقة . لسوء الحظ ، في الممارسة العملية ، كانت هذه الطريقة لا تزال جيدة مثل طريقة البسيط أو طريقة النقاط الداخلية.
ولكن في الواقع كيف يعمل
ولل
طريقة النقطة الداخلية
هذه الطريقة لها تاريخ طويل من التطور ، وقد ظهر أحد الشروط الأساسية في نفس الوقت الذي تم فيه تطوير طريقة simplex. ولكن في ذلك الوقت لم تكن فعالة بما يكفي لاستخدامها في الممارسة العملية. في وقت لاحق من عام 1984 ، تم تطوير مجموعة
متنوعة من الطريقة خصيصًا للبرمجة الخطية ، والتي كانت جيدة من الناحية النظرية والممارسة. علاوة على ذلك ، لا تقتصر طريقة النقاط الداخلية فقط على البرمجة الخطية ، على عكس الطريقة البسيطة ، والآن هي الخوارزمية الرئيسية لمشاكل التحسين المحدبة مع القيود.
الفكرة الأساسية للطريقة هي استبدال القيود بغرامة في شكل ما يسمى
وظيفة الحاجز . الوظيفة
F:Int mathcalK rightarrow mathbbR تسمى
وظيفة الحاجز للمجموعة
mathcalK إذا
F(x) rightarrow+ infty mboxatx rightarrow جزئي mathcalK.
هنا
Int mathcalK - بالداخل
mathcalK ،
جزئي mathcalK - الحدود
mathcalK . بدلاً من المشكلة الأصلية ، يُقترح حل المشكلة
mboxتصغيربمقدارx varphi(x،t)=tf(x)+F(x).
F و
varphi تعطى فقط من الداخل
mathcalK (في الواقع ، هذا هو المكان الذي يأتي منه الاسم) ، تضمن خاصية الحاجز ذلك
varphi على الأقل
x موجود. علاوة على ذلك ، أكثر
t كلما زاد التأثير
f . في ظل ظروف معقولة إلى حد معقول ، يمكنك تحقيق ذلك إذا كنت تهدف
t إلى ما لا نهاية ثم الحد الأدنى
varphi سوف تتلاقى إلى حل المشكلة الأصلية.
إذا كانت المجموعة
mathcalK نظرا لمجموعة من عدم المساواة
gi(x) leq0، 1 leqi leqm عندها يكون الاختيار المعياري لوظيفة الحاجز هو
الحاجز اللوغاريتميF(x)=− summi=1 ln(−gi(x)).
الحد الأدنى من النقاط
x∗(t) الوظائف
varphi(x،t) لمختلف
t يشكل منحنى ، والذي يسمى عادة
المسار المركزي ، طريقة النقطة الداخلية ، كما كانت ، تحاول اتباع هذا المسار. هكذا تبدو
أمثلة البرمجة الخطية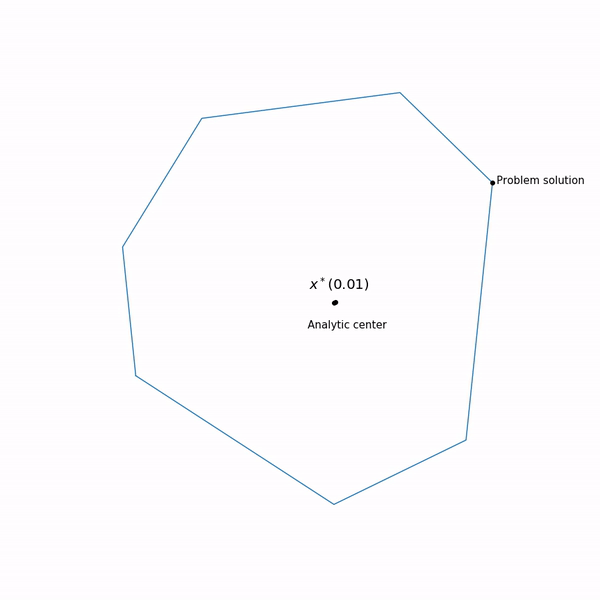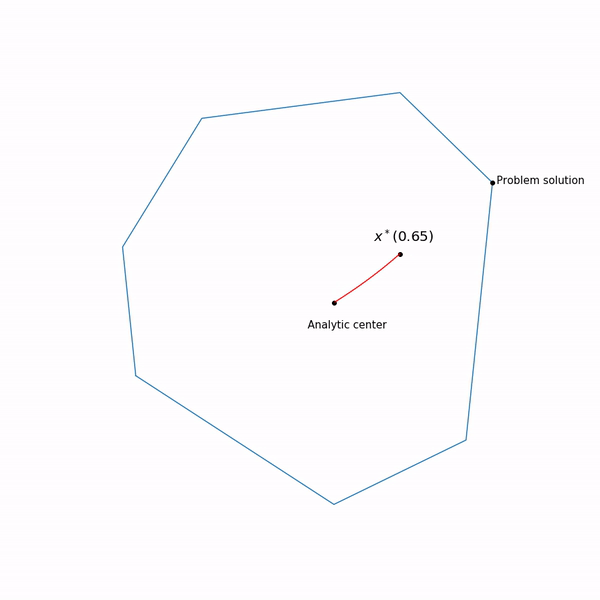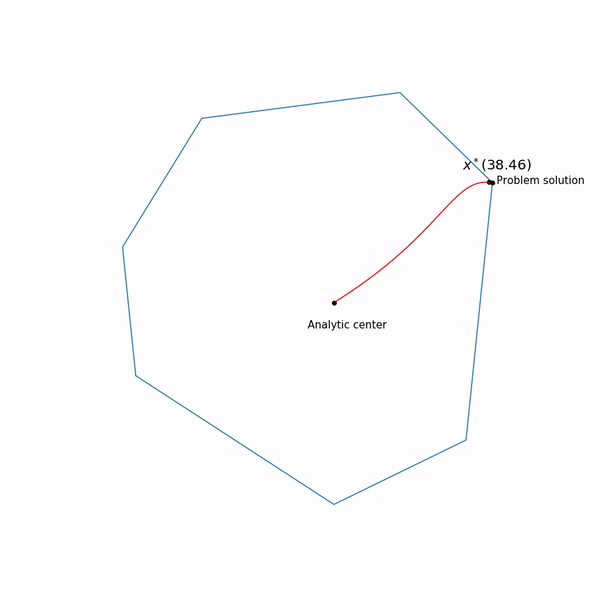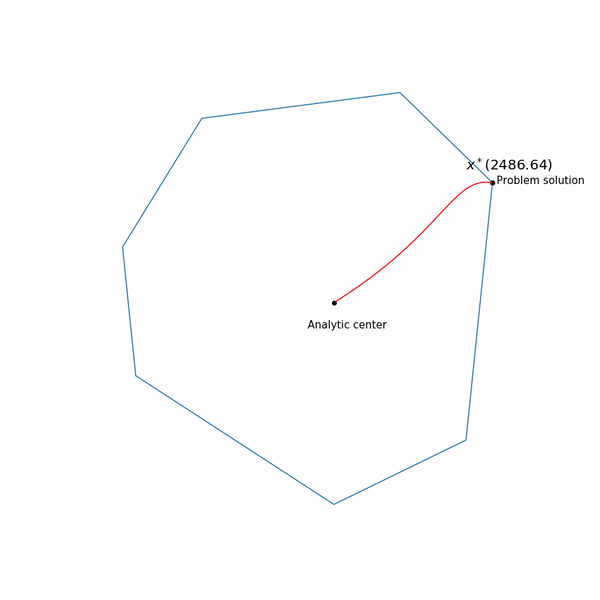 المركز التحليلي
المركز التحليلي عادل
x∗(0) وأخيرًا ، فإن طريقة النقاط الداخلية نفسها لديها الشكل التالي
- حدد تقريبًا مبدئيًا x0 ، t0>0
- اختر تقريب جديد باستخدام نيوتن
xk+1=xk−[ nabla2x varphi(xk،tk)]−1 nablax varphi(xk،tk)
- اضغط للتكبير t
tk+1= alphatk، alpha>1
إن استخدام طريقة نيوتن هنا مهم جدًا: الحقيقة هي أنه مع الاختيار الصحيح لوظيفة الحاجز ، تولد خطوة طريقة نيوتن نقطة
تبقى داخل مجموعتنا ، وقد جربناها ، ولا تعطي دائمًا في هذا الشكل. وأخيرًا ، هذه هي الطريقة التي يبدو بها مسار طريقة النقاط الداخلية
مهمة البرمجة الخطيةالنقطة السوداء المرتدة هي
x∗(tk) ، أي النقطة التي نحاول أن نقترب من خطوة طريقة نيوتن في الخطوة الحالية.