في عام 2018 ، أجرينا ثلاث مسابقات لـ Yandex.Blitz - في التعلم الآلي ، وتطوير الأجهزة المحمولة ، والواجهة الأمامية. المسابقة الثالثة أقيمت مؤخراً - مبروك للفائزين! في هذه الأثناء ، نريد العودة إلى الجزء الثاني منها ، حيث تم اقتراح المهام عند تقاطع الخوارزميات وكتابة البرامج لنظامي التشغيل Android / iOS. سيستفيد المرشحون لمنصب مطور الهاتف المحمول في Yandex من الخبرة في حل مثل هذه المشاكل. اقرأ التحليل التفصيلي لبعضها. وإذا لم تشارك في Blitz ، فمن الأفضل أولاً محاولة حلها بنفسك .

مهمة "توريد الغاز"
| أدخل | الخلاصة | المهلة | حد الذاكرة |
|---|
| الإدخال القياسي أو input.txt | الإخراج القياسي أو output.txt | 15 ثانية | 15 ميغا بايت |
تعمل Nika على تطوير تطبيق لكبار المديرين في شركة غاز كبرى لمساعدتهم على التخطيط للإنتاج.
تدرس الشركة n الحقول التي تبعد d 1 ... d i ... d n كيلومترًا عن خط الأنابيب ويمكنها إنتاج وحدات غاز v 1 ... v i ... v n . يتم بيع ترخيص منفصل لكل حقل - التراخيص s 1 ... s i ... s n .
لربط الحقول بالطريق السريع ، تحتاج إلى بناء خطوط الأنابيب. المقاول الذي يمكنه وضع أنواع مختلفة من الأنابيب يساعد هذه الشركة. تختلف الأنابيب عن بعضها البعض في الطول (l 1 ... l i ... l m ) والسعر (p 1 ... p i ... p m ). يمكن دمجها مع بعضها البعض كما تريد.
تمتلك الشركة k عملات معدنية وتريد الحصول على أكبر قدر ممكن من الغاز.
كم ستكون الشركة قادرة على الإنتاج إذا أعطت المقاول أوامر مثالية؟
قد يكون خط الأنابيب أطول من المسافة من الحقل إلى خط الأنابيب.
يحتوي السطر الأول على عدد صحيح k ≤ 10 5 .
يحتوي السطر الثاني على عدد صحيح n ≤ 15.
تحتوي الأسطر n التالية على ثلاثة أعداد صحيحة d i ≤ 100 و v i ≤ 100 و s i ≤ 100.
يتم فصل الأرقام بمسافة.
يحتوي السطر التالي على عدد صحيح m ≤ 15.
تحتوي السطور m التالية على عددين صحيحين l i ≤ 100 و p i ≤ 100. يتم فصل الأرقام بمسافة.
السطر الوحيد مع الجواب.
أمثلة
| أدخل | الخلاصة |
116
3
58 7 50
81 71 56
52 57 31
3
47 9
1 25
18 61 | 57 |
التحليل
بادئ ذي بدء ، دعنا نحدد الترميز. يجب ألا يكون هناك فئة من الكائنات إيداع (إيداع) مع المعلمات $ inline $ Dd_ {i} $ مضمنة $ (بعد) $ inline $ Dv_ {i} $ مضمنة $ (حجم الإنتاج) و $ inline $ Ds_ {i} $ مضمنة $ (تكلفة الترخيص). ستكون كائنات الفهرس من هذا النوع المتغير i. هناك أيضًا فئة كائن Pipeliner مع معلمات $ inline $ PPl_ {j} $ مضمنة $ (طول الأنبوب الذي يمكن للمقاول أن يبنيه) و $ inline $ PPp_ {j} $ مضمنة $ (سعر هذا الأنبوب) ، الفهرس من خلال ي. سأل المشاركون في الغارة عدة مرات ما إذا كان يمكن استخدام نوع واحد من الأنابيب مرتين. من المفترض أن لا ، وهذا المثال يظهر بوضوح. حتى بشروط هذه المهمة ، قبول $ inline $ D_ {i} = {0، 1} $ inline $ (اختر مجالا أم لا) و $ inline $ PP_ {j} = {0، 1} $ inline $ (اختر مقاولًا أم لا) ، يمكنك إجراء مهمة برمجة خطية:
$ inline $ \ sum \ limits_ {i} D_ {i} * Dv_ {i} \ rightarrow max \\ \ sum \ limits_ {i} D_ {i} * Ds_ {i} + \ sum \ limits_ {j} PP_ { j} * PPp_ {j} \ leq k \\ \ sum \ limits_ {i} D_ {i} * Dd_ {i} \ leq \ sum \ limits_ {j} PP_ {j} * PPl_ {j} \\ D_ { i} = {0، 1}، PP_ {j} = {0، 1} $ inline $
يمكن حلها ، على سبيل المثال ، عن طريق طريقة البسيط. ومع ذلك ، وفقًا لشروط المهمة ، نحن مطالبون بإرجاع الحد الأقصى لحجم الإنتاج فقط (أي قيمة الوظيفة الهدف) وليس مطلوبًا الإشارة إلى الحقول والمقاولين الذين يجب اختيارهم. إلى جانب القيود في الحالة ، يمكن حل المشكلة عن طريق طريقة البرمجة الديناميكية من خلال إنشاء جدول dp [length] [money] ، حيث يكون الطول هو طول خط الأنابيب ، والمال هو المال. بعد البناء الصحيح للجدول ، يكفي العثور على القيمة القصوى فيه ، والتي ستكون الإجابة. قيود الذاكرة للمهمة كافية للبناء.
مهمة "الأبراج والذكاء الاصطناعي"
| أدخل | الخلاصة | المهلة | حد الذاكرة |
|---|
| الإدخال القياسي أو input.txt | الإخراج القياسي أو output.txt | ثانية واحدة | 64 ميغا بايت |
يعمل Artem على تطوير ذكاء اصطناعي يلعب لعبة جوّال تنافسية. قواعد اللعبة بسيطة.
أمام اللاعبين يوجد أبراج n بارتفاع c 1 ... c i ... c n . من جانبه ، يمكن للاعب كسر أحد الأبراج بحيث يتم الحصول على عدة أبراج أصغر. يخشى اللاعبون الخلط في الأبراج ، لذلك اتفقوا على تقييد: بعد الانفصال ، لا يجب الحصول على برجين من نفس الارتفاع. على سبيل المثال ، يمكن تقسيم برج بارتفاع 7 إلى (1 ، 2 ، 4) ، ولكن ليس إلى (1 ، 3 ، 3). الارتفاع دائمًا عددًا صحيحًا.
يفقد من ليس لديه أبراج يمكن تدميرها.
لدى Artem صديق ذكي للغاية يلعب بشكل مثالي - حيث يحارب الذكاء الاصطناعي في Artem. لتقييم عمل الذكاء الاصطناعي ، تحتاج Artyom إلى معرفة ما إذا كان يجب أن يفوز الروبوت إذا كان كلا اللاعبين يتصرفان على النحو الأمثل. مساعدته في هذا.
الإنسان يمشي أولاً أولاً. سيلعب مع ألعاب AI k.
يحتوي السطر الأول على عدد صحيح k <500.
ويتبع ذلك كتل k من سطرين.
السطر الأول من كل كتلة هو عدد صحيح 0 <n ≤ 50.
يحتوي السطر الثاني من كل كتلة على عدد صحيح n 0 <c i ≤ 50. يتم فصل الأرقام بفراغات.
خطوط k ، يحتوي كل منها على صواب أو خطأ ، اعتمادًا على ما إذا كان الشخص سيفوز باللعبة.
أمثلة
| أدخل | الخلاصة |
2
1
4
2
1 1 | خطأ
خطأ |
التحليل
لعبة البرج المقترحة هي لعبة نهاية عادلة للاعبين لا يمكن التعادل فيها.
لذلك ، يتم تحديد فوز لاعب معين في اللعبة حسب حالة اللعبة وترتيب تحركات اللاعبين. بالنسبة للقراء الذين هم على دراية بنظرية اللعبة ، من الواضح أن أيًا من الألعاب المتساوية للاعبين تعادل في الواقع لعبة "له" ، مما يعني لعبتنا أيضًا.
هنا وصف موجز للعبة له ( رابط للمصدر - انقر عليها لمراجعة مفصلة):
هناك عدة أكوام ، لكل منها عدة أحجار. في خطوة واحدة ، يمكن للاعب أخذ أي عدد من الأحجار غير صفرية من أي كومة واحدة ورميها بعيدًا. وفقًا لذلك ، تحدث الخسارة عندما لا يكون هناك المزيد من الحركات المتبقية ، أي جميع الأكوام فارغة.
لذلك ، يتم وصف حالة لعبة "له" بشكل فريد من خلال مجموعة غير مرتبة من الأرقام الطبيعية. في خطوة واحدة ، يُسمح بتقليص أي من الأرقام بدقة (إذا أصبح الرقم نتيجة لذلك ، يتم إزالته من المجموعة).
الحل للعبة نيم هو العثور على مجموع xor من حجم الأكوام ، وفقط إذا كان هذا المبلغ غير صفري ، يمكننا أن نوضح بوضوح أننا في حالة فوز.
علاوة على ذلك ، تأتي نظرية Sprag-Grandi لمساعدتنا ، والتي تنص على أن الحالة U لأي لعبة متساوية من لاعبين يمكن أن ترتبط مع عدد قليل من ألعابه من الحجم X. بمجرد أن تكون وظيفة تحديد خريطة حالات لعبتنا له لعبة ، سيتم تقليل حل المشكلة لحلها - لعبة معروفة بالفعل.
مهمة "مؤشر التصنيف"
| أدخل | الخلاصة | المهلة | حد الذاكرة |
|---|
| الإدخال القياسي أو input.txt | الإخراج القياسي أو output.txt | ثانية واحدة | 64 ميغا بايت |
تقوم جاليا بتطوير مجمع مراجعة. قررت تحديد تصنيفات المؤسسات بمساعدة النجوم السبعة.
يتلقى نظام عرض الإدخال مستطيلًا من الارتفاع h والعرض w ، يقع الزاوية اليسرى العليا منه عند النقطة (x ، y). يجب رسم النجم وفق القواعد التالية:
- يتم تحديد حجم النجم من خلال عرض أو ارتفاع المستطيل - أي أصغر. (انظر الرسوم.)
- إذا كان أحد أبعاد المستطيل أكبر من البعد المقابل للنجم ، فيجب أن يتمركز النجم على هذا البعد.
- النجم مدبب.
يتوقع نظام التقديم إحداثيات رؤوس النجم من كود غالي. مساعدة غيل لحسابها.
لبناء نجمة ذات سبع رؤوس ، يأخذ Galya المحيط الخارجي للشكل الذي تم الحصول عليه عن طريق توصيل رؤوس مسبار منتظم من خلال واحد. في نظام الإحداثيات ، يتم توجيه المحور X من اليسار إلى اليمين ، والمحور Y من الأعلى إلى الأسفل. لا يتعطل برنامج Gali ، ويتلقى قيم عرض وارتفاع غير صحيحة كمدخلات.
يحتوي سطر واحد على أعداد صحيحة x و y و w و h مفصولة بمسافات.
مثال: يشير الإدخال 150 0 50 100 إلى مستطيل بعرض 50 نقطة وارتفاع 100 نقطة والزاوية العلوية اليسرى عند النقطة (150 ، 0).
السطر الوحيد الذي يحتوي على 28 رقمًا مفصولة بمسافات هو إحداثيات رؤوس النجم ، بدءًا من الأعلى ثم باتجاه عقارب الساعة. يجب تقريب الأرقام إلى أقرب عدد صحيح. شاهد مثالاً على الإخراج وتوضيحًا للمشكلة قبل متابعة الحل.
مثال: يجب أن يكون ناتج ثلاث نقاط (1 ، 2) ، (3 ، 4) ، (5 ، 6) كما يلي: 1 2 3 4 5 6.
أمثلة
| أدخل | الخلاصة |
0 0 100 100 | 50 1 65 21 90 21 85 45100 64 78 75 72 99 50 88 28 99 22 75 0 64 15 45 10 21 35 21 |
ملاحظات
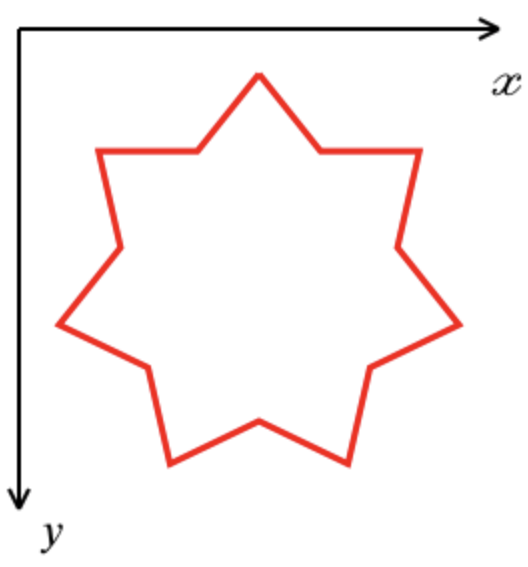
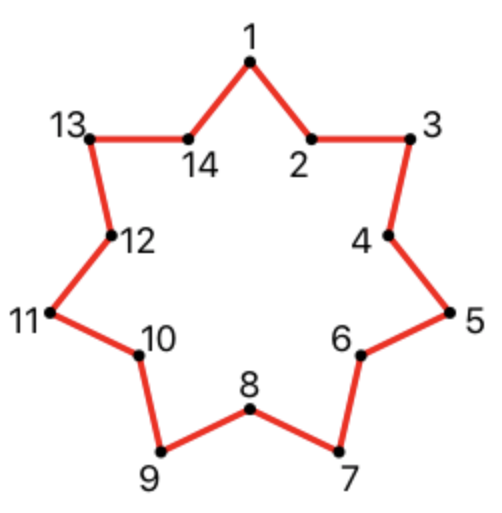
أمثلة على النجوم المنقوشة:
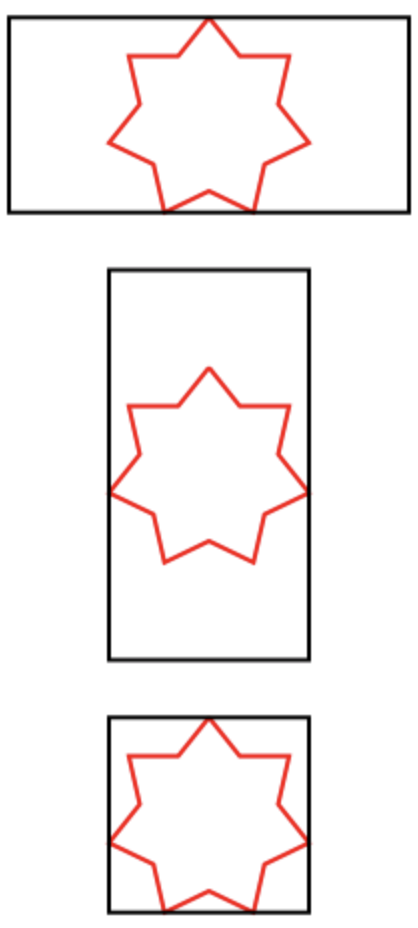
التحليل
يتم تقليل حل المشكلة إلى ثلاث مراحل: لبناء نجمة مرجعية مع الاتجاه المطلوب في الفضاء ، وقياس النقاط الناتجة ، وحساب وتطبيق الإزاحة.
بناء نجم
أسهل طريقة هي بناء نجمة منقوشة في دائرة نصف قطرها متمركز في الأصل. يتم حساب نقاط القمم الخارجية باستخدام علم المثلثات التافه ، ولكن مع النقاط الداخلية تكون المهمة أكثر تعقيدًا. يمكن العثور عليها بطريقتين على الأقل. أسهل طريقة هي العثور على تقاطعات الأجزاء التي تربط القمم الخارجية. الأكثر تعقيدًا هو إيجاد صيغة لحساب نصف قطر دائرة منقوشة من نصف قطر دائرة محدودة. أسهل طريقة للقيام بذلك هي أولاً ، على سبيل المثال ، للنجم الخماسي ، ومعممة للنجم N-point مع وجود فجوة تعسفية بين القمم المتصلة.
تحجيم
في جميع الحالات ، يتم إعطاء الحجم الذي نحتاجه لتناسب النجم. وبالتالي ، نحتاج إلى قياس النقاط التي تم الحصول عليها بحيث لا تتجاوز المسافة من أقصى اليسار إلى أقصى اليمين العرض المحدد ، ولا تتجاوز المسافة من الأعلى إلى الأدنى الارتفاع المحدد. نأخذ عوامل التحجيم لجلب العرض والارتفاع إلى القيم المطلوبة ، وتحديد القيم الأصغر. نظرًا لأننا بنينا نجمًا مرجعيًا بحكمة مع المركز في الأصل ، يكفي ببساطة مضاعفة إحداثيات كل نقطة في المعامل المحدد.
تعويض
آخر شيء متبقي هو تحريك نقاطنا بحيث يكون النجم داخل الإطارات المحددة. يمكن تقليل بيانات الإدخال لجميع الخيارات إلى مربع محيط بإحداثيات معينة من الزاوية اليسرى العليا. كل شيء بسيط هنا: نأخذ أعلى نقطة من النتائج التي تم الحصول عليها في المرحلة الأخيرة ، ونأخذ في الاعتبار اختلاف إحداثيات ص مع إحداثيات ص في الزاوية اليسرى العليا ، ونحول جميع النقاط عموديًا بالقيمة التي تم الحصول عليها. نفعل نفس الشيء مع إحداثيات س ، لا نأخذ فقط النقطة الأعلى ، بل النقطة اليسرى. هناك لمسة أخيرة: توسيط النجم في هذا المستطيل.
تعتمد الإجراءات الإضافية على المعامل الذي اخترناه في المرحلة السابقة:
- إذا تم قياس الارتفاع - فنحن نأخذ الفرق بين عرض المستطيل والمسافة من اليسار إلى أقصى اليمين ؛
- إذا تم قياس العرض - فنحن نأخذ الفرق بين ارتفاع المستطيل والمسافة من أعلى إلى أدنى نقطة.
اقسم القيمة التي تم الحصول عليها على 2 وقم بتحويل النقاط وفقًا للقياس المقابل. تم تلقي الإجابة.
مهمة "دوران وتحجيم دائرة"
| أدخل | الخلاصة | المهلة | حد الذاكرة |
|---|
| الإدخال القياسي أو input.txt | الإخراج القياسي أو output.txt | ثانية واحدة | 64 ميغا بايت |
تعمل Vika على تطوير محرر رسومات للهواتف الذكية والأجهزة اللوحية. تريد منح المستخدم الفرصة لتدوير دائرة على الشاشة بإصبعين وتغيير حجمها ، كما يلي:
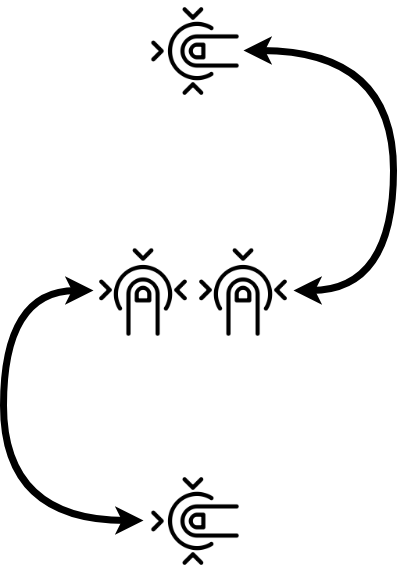
يدور الشكل بنفس الزاوية التي يدور بها الجزء الذي يربط الأصابع. يتغير حجم الشكل بما يتناسب مع طول المقطع. أولاً ، يتم تدوير الشكل ، ثم يتم تغيير حجمه. في البداية ، تحتوي الدائرة على إحداثيات (س ، ص) ونصف قطر ص. يتم تقديم قائمة بأحداث اللمس التي تصف إيماءة المستخدم. ساعد Vika في حساب الإحداثيات النهائية لمركز الدائرة ونصف قطرها. تدور الدائرة بالنسبة للنقطة (أ ، ب).
يحتوي وصف حدث اللمس على معرف الإصبع والإحداثيات ونوع الحدث. الإصبع الأول الذي يعلقه المستخدم يتلقى id 0 ، والثاني - id 1 ، وهكذا.
مثال:
0 337490 ACTION_DOWN - هذا يعني أنه مع وجود الإصبع 0 عند النقطة (337 ، 490) حدث الحدث ACTION_DOWN.
أحداث اللمس من الأنواع التالية:
- ACTION_DOWN - قام المستخدم بتطبيق الإصبع الأول على الشاشة عند نقطة معينة.
- ACTION_POINTER_DOWN - وضع المستخدم إصبعًا ثانيًا على الشاشة عند نقطة معينة.
- ACTION_MOVE - حرك المستخدم إصبعه إلى نقطة معينة.
- ACTION_POINTER_UP - نقل المستخدم الإصبع الثاني إلى النقطة المحددة وأطلقه.
- ACTION_UP - نقل المستخدم الإصبع الأول إلى النقطة المحددة وأطلقه.
- ACTION_CANCEL - إيماءة إجهاض المستخدم.
يحتوي السطر الأول على الأرقام x و y و r ، مفصولة بمسافات. يحتوي السطر الثاني على الأرقام أ و ب ، مفصولة بمسافات. تحتوي الأسطر القليلة التالية على أحداث لمس متتالية.
الخط الوحيد مع الإحداثيات ونصف القطر. يتم فصل الأرقام بمسافات.
مثال
| أدخل | الخلاصة |
252 194 78
445،559
0 337،490 ACTION_DOWN
1،599،490 ACTION_POINTER_DOWN
1،576،564 ACTION_MOVE
1،552،590 ACTION_MOVE
0 407،375 ACTION_MOVE
1 505 615 ACTION_MOVE
1 482620 ACTION_MOVE
0 477 360 ACTION_MOVE
1،435،616 ACTION_MOVE
1،411،607 إجراء ACTION_MOVE
0 547386 ACTION_MOVE
5464 364 1 ACTION_POINTER_UP
0 571 387 ACTION_UP | 831 704 73 |
ملاحظات
عند عرض النتيجة ، من الضروري تقريب جميع قيم الفاصلة العائمة إلى قيمة صحيحة وفقًا لقواعد التقريب الرياضي.
التحليل
على الرغم من حقيقة أن الإيماءة تبدو معقدة ، يمكن تقسيمها إلى مكونين: الدوران والقياس. لتدوير الشكل ، نحتاج إلى حساب زاوية الدوران ، والتي يمكن الحصول عليها باستخدام الصيغة التالية:
a = atan2 (prevTouchX2 - prevTouchX1، prevTouchY2 - prevTouchY1) - atan2 (currentTouchX2 - currentTouchX1، currentTouchY2 - currentTouchY1).
بعد تلقي زاوية التدوير ، تحتاج إلى تدوير الشكل نفسه ، مما يقلل من تحويل كل نقطة من الشكل بزاوية التدوير. بعد أن قمنا بتدوير الشكل ، نحتاج إلى توسيعه. تحجيم الرقم أمر تافه للغاية. من الضروري تذكر المسافة بين الإصبعين الأول والثاني عند تلقي حدث ACTION_POINTER_DOWN للإصبع الثاني ، وبعد ذلك ، من خلال تتبع المسافة بين الإصبعين الأولين ، يمكنك حساب المعامل الذي تحتاج إليه لقياس الشكل.
مهمة "بناء الطرق"
| أدخل | الخلاصة | المهلة | حد الذاكرة |
|---|
| الإدخال القياسي أو input.txt | الإخراج القياسي أو output.txt | ثانية واحدة | 64 ميغا بايت |
في لعبة الهاتف المحمول ، تبني الشخصية الرئيسية قاعدة على كوكب بعيد. يبدأ بالمحيط - الأبراج المتصلة بجدران الليزر المباشرة. يرسل له المهندسون المعماريون من المقر خطة توضح الأبراج n بالإحداثيات (x 1 ، y 1 ) ... (x i ، y i ) ... (x n ، y n ). من وجهة نظر الدفاع عن القاعدة ، لا معنى لوضع ثلاثة أبراج مجاورة أو أكثر على خط مستقيم واحد. ومع ذلك ، يقوم المهندسون المعماريون أحيانًا بوضع الأبراج بهذه الطريقة ، لذا يتعين على اللاعب نفسه إزالة الأبراج المتوسطة الإضافية.
بعد الانتهاء من المحيط ، يبدأ البطل في تجهيز القاعدة من الداخل. يريد بناء طرق k بين الأبراج - يمكن للطريق ربط أي برجين غير متجاورين ، ولكن لا يمكنه عبور طريق أو جدار آخر. يمكن أن تخرج العديد من الطرق من برج واحد.
البطل لديه روبوتات ع الطريق. لاختيار أفضل خطة لبناء الطرق ، يرشدهم البطل بالفرز عبر جميع الخيارات الممكنة. تبدأ الروبوتات في العمل في وقت واحد ومرة تلو الأخرى في نفس الوقت تجلب خيارات فريدة لموقع الطرق. إذا اتضح قبل التكرار التالي أن هناك خيارات أقل من الروبوتات ، يتم تحرير الروبوتات الإضافية وإرسالها إلى المطبخ لطهي العشاء. الروبوتات المتبقية تنهي الخيارات الأخيرة وتغلق.
إذا اتضح أنه يمكنك تمهيد الطريق خارج القاعدة ، يعلن البطل أن القاعدة غير آمنة ويطير بعيدًا عن الكوكب.
كم عدد الروبوتات التي ستعمل في المطبخ؟
يحتوي السطر الأول على ثلاثة أعداد صحيحة 4 ≤ n ≤ 10 7 ، 1 ≤ k ≤ n ورقم أولي 105 <p <11 × 104. يتم فصل الأرقام بفراغات.
تحتوي الأسطر n التالية على عدد صحيحين 0 <x i ، y i <109. يتم فصل الأرقام بمسافات.
السطر الوحيد مع الجواب. إذا لم تكن القاعدة آمنة ، فقم بطباعة −1.
مثال 1
| أدخل | الخلاصة |
4 1 101363
0 0
1 0
1 1
0 1 | 101361 |
هناك طريقتان لتمهيد الطريق الوحيد: (0 ، 0) - (1 ، 1) و (1 ، 0) - (0 ، 1). سيشارك فيها روبوتان ، وسيذهب الباقي إلى المطبخ: ص - 2 = 101 361.
مثال 2
| أدخل | الخلاصة |
4 1 101363
1 0
2 0
0 1
1 2 | -1 |
هنا يمكنك بناء طريق بين (1 ، 0) - (0 ، 1) ، وهذا خارج القاعدة. يتعرف البطل على القاعدة على أنها غير آمنة ، والإجابة هي −1.
مثال 3
| أدخل | الخلاصة |
4 1 101363
0 0
1 0
2 0
0 1 | 101363 |
الأبراج (0 ، 0) ، (1 ، 0) و (2 ، 0) على نفس الخط ، لذلك لن يقوم البطل ببناء البرج الأوسط (1 ، 0). لا يمكن تعبيد أي طريق ، لذلك ستذهب جميع الروبوتات فورًا إلى المطبخ: p = 101 363.
التحليل
نقسم حل المشكلة إلى ثلاث خطوات.
تتمثل الخطوة الأولى في تحديد مجموعة بيانات قمة الإدخال ما إذا كان المضلع محدبًا ، وإذا كان الأمر كذلك ، فكم عدد القمم الحقيقية الموجودة به. يكون المضلع محدبًا إذا كانت جميع رؤوسه موجودة على جانب واحد من الخط الذي يدعم أي حافة. لكل ثلاث رؤوس متجاورة $ inline $ (x_ {i-1} ، y_ {i-1}) ، (x_ {i} ، y_ {i}) ، (x_ {i + 1} ، y_ {i + 1}) $ مضمنة $ بناء بضعة نواقل $ inline $ ab = ((x_ {i-1} ، y_ {i-1}) ، (x_ {i} ، y_ {i})) و bc = ((x_ {i} ، y_ {i}) ، (x_ {i + 1} ، y_ {i + 1})) $ مضمنة $ ، واحسب علامة التعبير ab.x bc.y - bc.x ab.y. إذا كان التعبير يساوي 0 ، فإن القمم تقع على خط مستقيم واحد ، ووفقًا لحالة المشكلة ، يختفي البرج الواقف في قمة الوسط ، مما يقلل العدد الإجمالي للأبراج. إذا كانت علامة المنتج لكل ثلاث مرات من الرؤوس هي 0 أو دائمًا هي نفسها ، فانتقل إلى الخطوة الثانية ، إذا لم تكن كذلك ، فنحن نعتبر القاعدة غير آمنة ونطبع الإجابة -1.
الخطوة الثانية. عدد طرق بناء الأقطار المتقطعة k داخل محدبة N-gon هي $ inline $ V = 1 / (k + 1) {N-3 \ اختيار k} {N + k-1 \ اختيار k} $ مضمنة $ ، لكننا بحاجة إلى حساب التعبير p - V mod p ، حيث p هو رئيس.
تخيل N! كيف $ inline $ a * p ^ e $ مضمنة $ ، حيث يكون العامل المشترك الأكبر هو a ، و p gcd (a، p) = 1.
$ inline $ {n \ Choose r} = (n!) / (r! (nr)!) = a_ {1} * p ^ {e_ {1}} / a_ {2} * p ^ {e_ {2} } * a_ {3} * p ^ {e_ {3}} = (a_ {1} / a_ {2} * a_ {3}) * p ^ {e_ {1} -e_ {2} -e_ {3} } $ مضمنة $
إذا $ inline $ e_ {1} -e_ {2} -e_ {3}> 0 $ مضمنة $ ، ثم التعبير قابل للقسمة على p والإجابة في المشكلة هي p.
للحالة $ inline $ e_ {1} -e_ {2} -e_ {3}> 0 $ مضمنة $ = 0 ستكون الإجابة $ inline $ a_ {1} / a_ {2} * a_ {3} $ inline $ ص ص.
في الحساب ، نأخذ في الاعتبار أن b mod p = (a mod p) (b mod p) mod p ، و $ inline $ k ^ {- 1} $ مضمنة $ mod p = $ inline $ (k) ^ {p-2} $ مضمنة $ وزارة الدفاع ص لرئيس ص.
الخطوة الثالثة. لحساب التعبير $ inline $ e_ {1} -e_ {2} -e_ {3} $ inline $ تخيل ن! كـ 1 2 ... p (p + 1) ... 2p (2p + 1) ... ، بينما (p + 1) ... (2p-1) mod p = 1 2 ... (p-1 ) = (p-1)! .. المجموع ، n mod p = ( $ inline $ (p-1)! ^ k $ inline $ k (n mod p)!) mod p ، حيث k = floor (n / p).
مهمة "جدولة بسيطة للغاية"
| أدخل | الخلاصة | المهلة | حد الذاكرة |
|---|
| الإدخال القياسي أو input.txt | الإخراج القياسي أو output.txt | 10 ثواني | 224 ميغا بايت |
هناك مهام n للقيام بها على معالج الهاتف الذكي. يتطلب تنفيذها t 1 ... t i ... t n من وحدات الزمن ، وبحلول بداية الوحدة الزمنية d ، يجب الانتهاء من المهمة i.
في الوقت المناسب ، يمكن تنفيذ المهام في العديد من الخيوط ، ومع ذلك ، يؤدي كل خيط جديد إلى زيادة الحمل على البطارية. في التيار الأول ، يتم استهلاك وحدة من الطاقة لكل وحدة زمنية ، في وحدة واحدة ونصف من الطاقة ، في المرة الثالثة ونصف مرة أكثر من الثانية ، إلخ.
يمكن تقسيم المهام إلى وحدات زمنية: أولاً ، أكمل واحدة جزئيًا ، ثم تنتقل إلى أخرى ، ثم العودة إلى الأولى. لا يمكنك تنفيذ أجزاء مختلفة من مهمة في سلاسل رسائل مختلفة في نفس الوقت.
يتلقى المجدول المهام واحدًا تلو الآخر ؛ بعد أن تلقى مهمة ، يقوم على الفور بتخصيص فترات زمنية لها. بعد توزيع المهمة ، لا يمكن للجدولة نقلها إلى فتحات أخرى.
ما مقدار الطاقة المطلوبة لإكمال جميع المهام إذا تم توزيعها على النحو الأمثل؟
السطر الأول يحتوي على العدد الصحيح 1 <n ≤ 3 × 10 3 .
تحتوي السطور n التالية على عددين صحيحين 0 ≤ t i ≤ 10 4 و 0 i d i ≤ 10 4 . يتم فصل الأرقام بمسافات.
السطر الوحيد مع الجواب. الدقة - ثمانية منازل عشرية.
مثال
| أدخل | الخلاصة |
5
2 2
1 1
3 4
1 10
1 2 | 10.25000000 |
التحليل
نظرًا لأنه وفقًا لظروف المشكلة ، يكفي لنا حساب كمية الطاقة المستهلكة فقط ، يمكننا استخدام طريقة الحل عن طريق حساب كمية الطاقة المستهلكة لكل وحدة زمنية. عند التخطيط للمهمة ، نأخذ الحد الأدنى لقيمة الطاقة المستهلكة k = 1 ، بدءًا من الموعد النهائي للمهمة ، نقوم بالفرز عبر جميع فترات الفترة الزمنية.
إذا كان استهلاك الطاقة للفتحة أقل من المعامل (k) ولم يتم استخدام هذه الفترة الزمنية عند التخطيط للمهمة ، فإننا نشغل هذه الفتحة لإكمال المهمة عن طريق زيادة معامل الفتحة بواسطة K. عندما نصل إلى بداية الفترة الزمنية ، نحتاج إلى زيادة معامل k بمقدار 1.5 مرة و كرر البحث عن الفترات الزمنية ، بدءًا من الموعد النهائي وحتى التخطيط للمهمة بالكامل. عند الانتهاء من التخطيط لجميع المهام ، يبقى فقط لحساب إجمالي استهلاك الطاقة عن طريق إضافة المعاملات التي تم الحصول عليها لكل وحدة زمنية.
مهمة الكائنات القابلة للتدمير
| أدخل | الخلاصة | المهلة | حد الذاكرة |
|---|
| الإدخال القياسي أو input.txt | الإخراج القياسي أو output.txt | 2 ثانية | 64 ميغا بايت |
2D- . , : n- (x 1 , y 1 )...(x i , y i )...(x n , y n ). — , . . , — , .
, [0 1 2 3 4], 1 3 1 3, [1 2 3] [0 1 3 4].
, . . , , .
, ?
n ≤ 500. n x y. .
. — .
مثال 1
| الخلاصة |
4
100 100
200 100
200 200
100 200 | 0.000000 |
مثال 2
| الخلاصة |
6
167 84
421 84
283 192
433 298
164 275
320 133 | 326.986753 |
, , . « » : — . : , ( ) .
, ? ( , , ). : , , , . , , ( ) . even-odd rule: . — , ( ) , — .
, , — , . (, , ):
- ( );
- : , - ;
- ( , 10-5 );
- even-odd rule — ;
- : 180 .
«DNA»
| الخلاصة | | |
|---|
| input.txt | output.txt | 8 | 128 |
, . , , . n . , . : A, T, G C. . .
n. n . . 6⋅10 6 .
. . . . . , .
( , ):
5
TTT
GAAGCT
CAAT
AGA
AGGCA
:
2 TTT
6 AGA
28 AGA
30 AGA
57 CAAT
86 AGA
100 GAAGCT
190 TTT
191 TTT
196 AGA
219 TTT
232 AGA
271 TTT
284 TTT
285 TTT
298 TTT
320 TTT
330 TTT
331 TTT
342 TTT
373 AGA
397 AGA
488 AGA
509 AGA
524 AGA
565 TTT
574 AGA
605 AGA
625 CAAT
630 AGA
681 CAAT
718 TTT
719 TTT
744 AGGCA
754 AGA
784 AGA
808 TTT
821 CAAT
833 AGA
861 CAAT
879 AGA
921 AGA
955 AGA
, . — , — . , . . , .
, .
«QR Quest»
| الخلاصة | | |
|---|
| input.txt | output.txt | 1 | 64 |

t, . t n i , .
t , .
مثال 1
| الخلاصة |
4
8 10 1 9 2 6 7 8
14 2 0 11 10 4 1 0
6 6 4 1 10 0 11 6
11 4 3 4 14 8 12 5 | 0
13
15
5 |
مثال 2
| الخلاصة |
4
9 10 6 2 12 11 7 2
3 10 1 14 13 13 1 1
6 8 8 5 3 2 6 4
5 11 5 5 3 1 10 7 | 3
9
2
7 |
, . QR- , . - .
تم إدخال ما مجموعه ثمانية أرقام - إحداثيات الخلايا في هذه الجداول ، أي 4 أزواج مع إحداثيات العمود والصف. كان من الضروري تخمين العملية التي أجريت مع هذه الخلايا ومن أي جدول خلية إضافية.
باستخدام التلاعب البسيط ، يمكن للمرء التحقق من أن هذا هو مجموع xor لأربع خلايا من الجداول A و B و C ، والتي تتم معالجتها بالمؤشرات a 0 ... a 7 :
R = A [a 0 ، a 1 ] ^ B [a 2 ، a 3 ] ^ B [a 4 ، a 5 ] ^ C [a 6 ، a 7 ].