كان الإنجاز الرياضي الرئيسي هو فرضية زيمر التي وجدها فريق صغير من الباحثين.
بالنسبة للشبكات ذات أبعاد التماثل الأعلى ، ليس من الممكن دائمًا الانتقال إلى أبعاد أقل من الرتبةيمكن تعريف نجاح روبرت زيمر بعدة طرق. بصفته
رئيسًا لجامعة شيكاغو منذ عام 2006 ، تصدر عناوين الأخبار ، حيث وجد مبالغ من تسعة أرقام لتمويل ونشر
المقالات لدعم حرية التعبير في الحرم الجامعي. ولكن قبل أن يصبح رئيسًا للجامعة ، كان عالم رياضيات. وبعد وقت طويل من تركه بحثًا جادًا ، أعطت خطة البحث التي أطلقها نتائجها أخيرًا.
قبل عام ،
أثبت ثلاثة من علماء الرياضيات
فرضية زيمر المتعلقة بالظروف التي تحتوي فيها المساحات الهندسية على تناظر من نوع معين. أصبح برهانهم أحد أكبر الإنجازات الرياضية في السنوات الأخيرة. إنه يضع نهاية للسؤال الذي نشأ قبل زيمر خلال نشاطه العقلي المكثف في أواخر السبعينيات وأوائل الثمانينيات.
قال زيمر: "أود أن أقول إنني أخلد إلى النوم خمس سنوات مع أفكار حول هذه المهمة ، كل ليلة ، لذلك كنت مهووسًا بها ، ومن الرائع مشاهدة كيف حلها الناس".
عادة ، كلما كانت مساحة البعد الهندسي أكبر ، كلما زادت التماثلات فيها. يمكن تخيل ذلك من خلال دراسة دائرة موجودة على مستوى ثنائي الأبعاد وكرة ممتدة في ثلاثة أبعاد: هناك طرق لتدوير الكرة أكثر من الطرق لتدوير الدائرة. أبعاد الكرة الإضافية تخلق تماثلات إضافية.
يشير تخمين زيمر إلى التماثلات من نوع خاص يعرف بالشبكات رفيعة المستوى. تتساءل عما إذا كان قياس المساحة الهندسية يحد من استخدام التماثلات من هذا النوع. أظهر مؤلفو العمل الجديد -
آرون براون وسيباستيان هورتادو سالازار من جامعة شيكاغو
وديفيد فيشر من جامعة إنديانا - أنه مع عدم وجود عدد من القياسات أقل من تناظر معين. وهكذا ، أثبتوا صحة فرضية زيمر.
طور روبرت زيمر ، رئيس جامعة شيكاغو ، فرضية سميت باسمه قبل 40 عامًا تقريبًايجيب عملهم على سؤال واحد مهم وطويل الأمد ، ويفتح طرقًا جديدة لدراسة العديد من الأسئلة الأخرى. كما يكشف عن الخصائص الجوهرية للمساحات الهندسية. التماثل هو أحد أبسط خصائص هذه المساحات. يقول العمل الجديد أن التماثلات يمكن أن توجد في مساحات من نوع واحد ، ولا يمكن أن توجد في أنواع أخرى. تم تحقيق هذا الإنجاز بعد عقود من التوقف.
قالت إيمي ويلكنسون ، عالمة الرياضيات في جامعة شيكاغو ، التي نظمت مؤتمر هذا العام حول هذا الدليل: "بدت الفرضية أنها يمكن أن تبقي الناس مشغولين لفترة طويلة جدًا". "وقد دمروا هذا السؤال ببساطة".
التماثلات المرضية
التماثل هو أحد المفاهيم الهندسية الأولى التي يصادفها الأطفال في الرياضيات. بأيديهم ، يتعلمون أنه يمكنك تدوير النموذج وقلبه وتحويله ، وفي النهاية الحصول على نفس الشكل الذي بدأوا به. إن الحفاظ على شكل الكائن نتيجة للتغييرات يستجيب برضا داخلي معين - هذا إشارة إلى ترتيب أعمق في الكون.
علماء الرياضيات لديهم لغتهم الرسمية الخاصة لدراسة التماثل. يمنحهم الفرصة للمناقشة بعبارات موجزة حول التماثلات المختلفة التي يمكن تطبيقها في مساحة هندسية معينة.
يحتوي المربع ، على سبيل المثال ، على ثمانية تماثلات - ثماني طرق لقلبه أو تدويره ، والحصول على المربع مرة أخرى. يمكن تدوير الدائرة بأي عدد من الدرجات ؛ لديها عدد لا نهائي من التماثلات. يجمع علماء الرياضيات جميع التماثلات لجسم هندسي معين ، أو مساحة ، ويجمعونها في "مجموعة".
المجموعات مثيرة للاهتمام في حد ذاتها. غالبًا ما تظهر نتيجة لدراسة بعض المساحات الهندسية ، ولكن في بعض الأحيان تظهر في سياق غير مرتبط تمامًا بالهندسة. على سبيل المثال ، يمكن أن تشكل المجموعات مجموعات رقمية (على سبيل المثال ، هناك تناظر معين في إضافة 5 أو طرح 5 من رقم).
قال زيمر: "يمكن للمجموعة ، من حيث المبدأ ، أن تظهر كتناظر لأشياء مختلفة تمامًا".
هناك أشكال غريبة أكثر من التناظر من تلك التي ندرسها في المدرسة. تأمل ، على سبيل المثال ، تناظر الشبكات. أبسط شعرية هي شبكة ثنائية الأبعاد. على متن الطائرة ، يمكن تحريك الشبكة لأعلى أو لأسفل أو لليسار أو لليمين بأي عدد من المربعات والحصول على شبكة تبدو تمامًا مثل الأصلية. يمكنك أيضًا عكس الشبكة من خلال أي عدد من الخلايا الفردية. تحتوي المساحات المزودة بالشبكات على عدد لا نهائي من التماثلات المختلفة للشبكات.
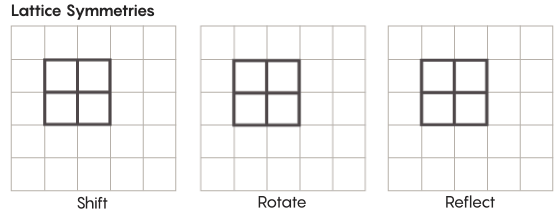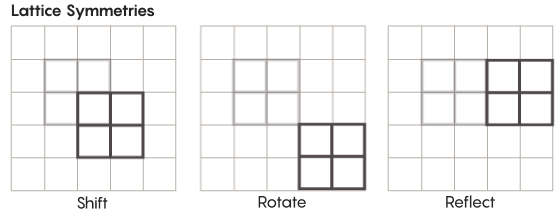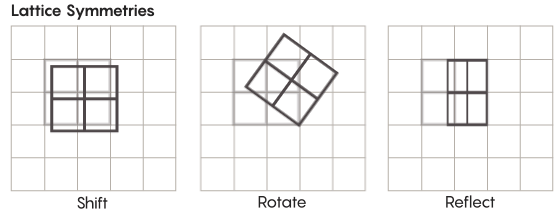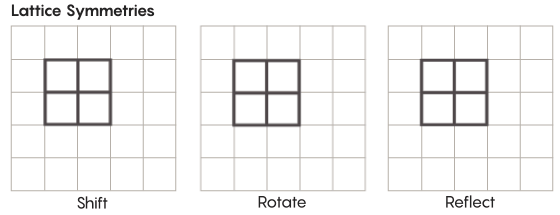
يمكن أن توجد المشابك في أي عدد من الأبعاد. في الفضاء ثلاثي الأبعاد ، قد تتكون الشبكة من مكعبات ، وليس مربعات. في أربعة أبعاد أو أكثر ، لن يكون من الممكن تقديم الشبكة ، ولكنها تعمل بنفس الطريقة ؛ يمكن لعلماء الرياضيات وصف ذلك بالضبط. تشمل المجموعات ذات الأهمية لفرضية زيمر المشابك "الرتب الأعلى" ، أو المشابك في مساحات معينة ذات أبعاد أعلى. قال خورتادو سالازار: "هذه الشبكة الغريبة ستكون جميلة جدًا ، إذا أمكن رؤيتها ، حتى لو لم يتم إعطائي إياها". "يبدو لي أن النظر إليها سيكون لطيفًا جدًا."
في القرن العشرين ، اكتشف علماء الرياضيات هذه المجموعات في ظل ظروف مختلفة - ليس فقط في الهندسة ، ولكن أيضًا في نظرية الأعداد والمنطق وعلوم الكمبيوتر. فتح مجموعات جديدة ، من المنطقي طرح السؤال - ما نوع المساحات التي تمتلك مثل هذه المجموعات من التماثلات؟
في بعض الأحيان يكون من المستحيل مطابقة المجموعات للمساحة. يمكن للمرء أن يفهم بسرعة أن مجموعة التماثلات في الدائرة لا يمكن تطبيقها على مربع. قم بتدوير المربع بمقدار 10 درجات ولن تحصل على المربع الأصلي. لكن مزيجًا من مجموعة ذات عدد لا نهائي من التماثلات والفضاء بأبعاد عديدة يجعل من الصعب تحديد قابلية تطبيق المجموعة.
قال زيمر: "عندما تنتقل إلى مجموعة أكثر تعقيدًا بأبعاد أكثر ، تصبح هذه القضايا معقدة للغاية".
اتصال غير مباشر
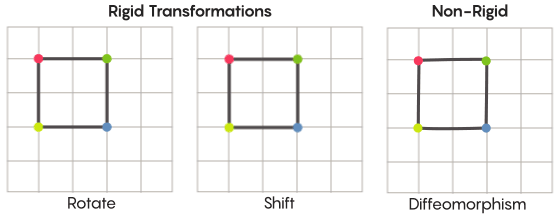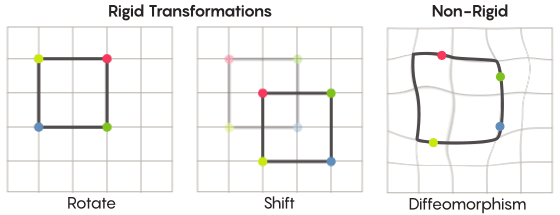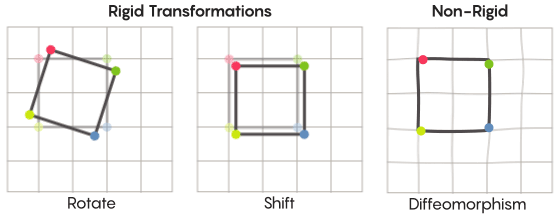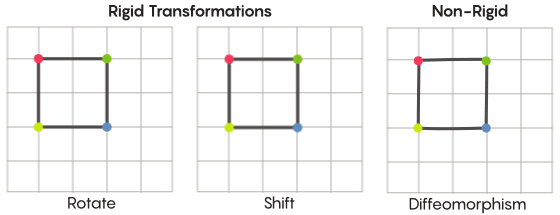
تخيل التناظر ، نتخيل دوران الشكل بأكمله - على سبيل المثال ، مربع مستدير 90 درجة. ولكن على المستوى الأساسي ، يعتمد التناظر على نقاط الحركة. التحول المتماثل للفضاء يعني أنك بحاجة إلى أخذ كل نقطة منه ونقلها إلى نقطة أخرى. وبهذا المعنى ، فإن تدوير المربع 90 درجة يعني في الواقع أنك بحاجة إلى أخذ كل نقطة من المربع وتدويرها 90 درجة بحيث لا تكون على الحافة التي بدأت منها.
ديفيد فيشريمكن حل مشكلة النقاط المتحركة بشكل أو بآخر. التحولات المتناظرة الأكثر شيوعًا - انعكاس مربع بالنسبة للقطر أو دورانه بمقدار 90 درجة - صارمة للغاية. صارمة بمعنى أنها لا تخلط النقاط. تبقى النقاط التي كانت رؤوسًا قبل الانعكاس رؤوسًا بعد (تصبح مجرد رؤوس مختلفة) ، والنقاط التي تشكل الحواف المستقيمة ، بعد الانعكاس ، لا تزال تشكل الحواف المستقيمة (مختلفة فقط).
هناك أنواع أقل صرامة وأكثر مرونة من التحولات المتناظرة ، وهي مثيرة للاهتمام في سياق فرضية زيمر. في مثل هذه التحولات ، تغير النقاط تنظيمها بشكل أقوى ؛ لا يحتفظون بالضرورة بصلاتهم السابقة مع بعضهم البعض بعد التحول. على سبيل المثال ، يمكنك تحريك كل نقطة من المربع بثلاث وحدات طول على طول محيط المربع - وهذا يفي بالمتطلبات الأساسية للتحول المتماثل ، أي ببساطة تحويل كل نقطة في الفضاء إلى مكان آخر. وصف آرون براون ، المؤلف المشارك للدليل ، كيف يمكن لهذه التحولات الأكثر حرية الشكل أن تبدو في سياق الكرة.
يمكنك أن تأخذ القطبين الشمالي والجنوبي وتحرفهما في اتجاهين متعاكسين. قال براون: "ستزيد المسافة بين النقاط".
في حالة الشبكة ، بدلاً من مجرد تحريكها على طول المستوى ، يمكنك ثنيها ، ومدها في بعض الأماكن والضغط عليها في أماكن أخرى ، بحيث لا تتداخل الشبكة المحولة بعد الآن مع الشبكة الأصلية. هذه التحولات أقل صرامة ، وتسمى اختلافات.
كان لدى زيمر سبب وجيه لاستخدام هذه النسخة الأقل صرامة من التناظر في فرضيته. تم دراسة المشابك الخاصة من أعلى رتبة تتعلق بهذه الفرضية لأول مرة في الستينيات من قبل
غريغوري ألكسندروفيتش مارجوليس ، الذي حصل على
جائزة الحقول لعمله. قدمت Margulis وصفًا كاملاً لنوع المساحات التي يمكن تحويلها باستخدام هذه المشابك ذات الرتب العالية ، إذا كان مسموحًا فقط بالتحولات الصارمة.
أصبحت فرضية زيمر استمرارًا طبيعيًا لعمل مارغوليس. يبدأ بقائمة من المساحات التي يمكن أن تعمل فيها المشابك ذات المستوى الأعلى - اكتشف Margulis هذه القائمة - ويسأل عما إذا كانت هذه القائمة تتوسع إذا كان مسموحًا للشبكات بتحويلات أقل صرامة.
في العمل الجديد ، أثبت ثلاثة من علماء الرياضيات أن إضعاف تعريف التناظر لا يغير نطاق تناسق المشابك ذات الترتيب العالي. حتى لو سمح للشبكات أن يكون لها تحولات غير منتظمة للغاية - للتحول والانحناء والتمدد - لا تزال المشابك لديها قيود صارمة على النطاق.
"بعد إضافة هذه المرونة إلى بيان المشكلة ، بالطبع ، بشكل بديهي ، يبدو أن الشبكات يمكن أن تعمل على نطاق أوسع. لذلك ، اتضح أنه من المفاجئ أنه في الواقع سيكون الجواب "لا" - في بعض الحالات لا يمكنهم ، "قال فيشر.
أسس علماء الرياضيات المراسلات الدقيقة بين أبعاد الفضاء والبعد ، أو رتبة الشبكات ، بالنسبة للشبكات التي يمكن أن تلعب دور التناظر في مساحة معينة. بشكل عام ، أظهروا أنه كلما ارتفع ترتيب الشبكة ، زادت الحاجة إلى قياسات للمساحة التي يمكنها استيعابها. حتى مع المرونة الكبيرة في تحويل الفضاء ، تقتصر تحويلات الشبكات الرفيعة المستوى على أبعاد أعلى.
قال ويلكينسون: "يشير هذا إلى أن هناك شيئًا أساسيًا للغاية في هيكل المساحات ، مما يعني ضمناً قدرتها على استيعاب مثل هذه التحولات".
إن فرضية زيمر ليست سوى الخطوة الأولى لبرنامج أكبر. بعد التعامل معها ، فرض المؤلفون المشاركون في العمل قيودًا تقريبية على المساحات التي يمكن أن تتحول فيها المشابك رفيعة المستوى. المرحلة التالية الأكثر طموحًا في العمل ستكون التركيز على تلك المساحات التي يمكن أن توجد فيها المشابك - ثم تصنيف جميع الطرق المختلفة لتحويل المشابك لهذه المساحات.
"في النهاية ، يجب أن يكون البرنامج قادرًا على تصنيف كل هذه الأساليب. وقال زيمر: "هناك العديد من الأسئلة المثيرة للاهتمام غير مجرد إنشاء حقيقة وجود أماكن معينة لا يمكن أن تعمل فيها الشبكات".