صور جوليا ومراحل النظم الديناميكية

نستمر في إتقان لغة جوليا الشابة والواعدة. لكن بالنسبة للمبتدئين ، نحتاج إلى الإمكانية الضيقة جدًا للتطبيق - لحل المشكلات الفيزيائية النموذجية. هذا هو التكتيك الأكثر ملاءمة لإتقان الأداة: من أجل الحصول على المساعدة ، سنقوم بحل المشاكل الملحة ، وزيادة التعقيد تدريجيًا وإيجاد طرق لجعل حياتنا أسهل. باختصار ، سنقوم بحل الاختلافات وبناء الرسوم البيانية.

للبدء ، قم بتنزيل حزمة رسومات Gadfly ، وعلى الفور النسخة الكاملة من المطور ، بحيث تعمل بشكل جيد مع Julia 1.0.1. نحن نقود في مفكرة REPL أو JUNO أو Jupyter:

using Pkg pkg"add Compose#master" pkg"add Gadfly#master" 

ليس الخيار الأكثر ملاءمة ، ولكن أثناء انتظار تحديث PlotlyJS ، يمكنك المحاولة من أجل المقارنة.

تحتاج أيضًا إلى أداة قوية لحل المعادلات التفاضلية

 ]add DifferentialEquations #     

هذه هي الحزمة الأكثر شمولاً والمدعومة التي توفر الكثير من الطرق لحلها. انتقل الآن إلى صور المرحلة.

غالبًا ما تكون حلول المعادلات التفاضلية العادية أكثر ملاءمة للتصوير بشكل غير عادي $$$y ^ 1 (t) ، ... ، y ^ L (t)$ ، وفي مساحة الطور على طول المحاور التي يتم رسم قيم كل من الوظائف التي تم العثور عليها. علاوة على ذلك ، يتم تضمين الحجة t في الرسوم البيانية فقط بشكل بارز. في حالة اثنين من ODEs ، مثل هذا الرسم البياني - صورة طور النظام - هو منحنى على مستوى الطور وبالتالي فهو واضح بشكل خاص.

مذبذب

ديناميكيات المذبذب التوافقي $$$\ gamma$ يوصف نظام المعادلات التالية:

وبغض النظر عن الشروط الأولية (x0، y0) ، فإنها تأتي إلى حالة توازن ونقطة (0،0) بزاوية انحراف صفرية وسرعة صفر.

في $$$\ gamma = 0$ يأخذ الحل الشكل المميز لمذبذب كلاسيكي.

 using DifferentialEquations, Gadfly #     -    function garmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) A = [0 1 -ω^2 γ] syst(u,p,t) = A * u # ODE system u0 = [x0, y0] # start cond-ns tspan = (0.0, 4pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end 

دعونا نحلل الرمز. تقبل الدالة قيم معلمة التردد والتوهين ، فضلاً عن الشروط الأولية. تحدد الدالة syst () المتداخلة النظام. من أجل أن يتحول ، استخدموا ضرب المصفوفة بسطر واحد. يتم تكوين وظيفة الحل () ، التي تأخذ عددًا كبيرًا من المعلمات ، بمرونة جدًا لحل المشكلة ، ولكننا أشرنا فقط إلى طريقة الحل - Runge-Kutta 4 ( هناك العديد من الميزات الأخرى ) ، والخطأ النسبي ، وحقيقة أنه لا يجب حفظ جميع النقاط ، ولكن كل ربع فقط . يتم تخزين مصفوفة الاستجابة في sol المتغير ، علاوة على ذلك ، sol.t يحتوي على متجه مرات ، و sol.u يحل النظام في هذه الأوقات. كل هذا يتم رسمه بهدوء في المؤامرات ، وبالنسبة لـ Gadfly ، يجب عليك إكمال الإجابة في مصفوفة أكثر ملاءمة. نحن لا نحتاج إلى أوقات ، لذا نعيد الحلول فقط.

دعونا نبني صورة طورية:

 Ans0 = garmosc() plot(x = Ans0[:,1], y = Ans0[:,2]) 

من بين الوظائف عالية الترتيب ، يعتبر broadcast(f, [1, 2, 3]) ملحوظًا بشكل خاص بالنسبة لنا ، والذي يستبدل قيم الصفيف [1 ، 2 ، 3] بالتناوب في الدالة f . تسجيل قصير f.([1, 2, 3]) . يفيد ذلك في تغيير التردد ومعلمة التوهين والإحداثيات الأولية والسرعة الأولية.

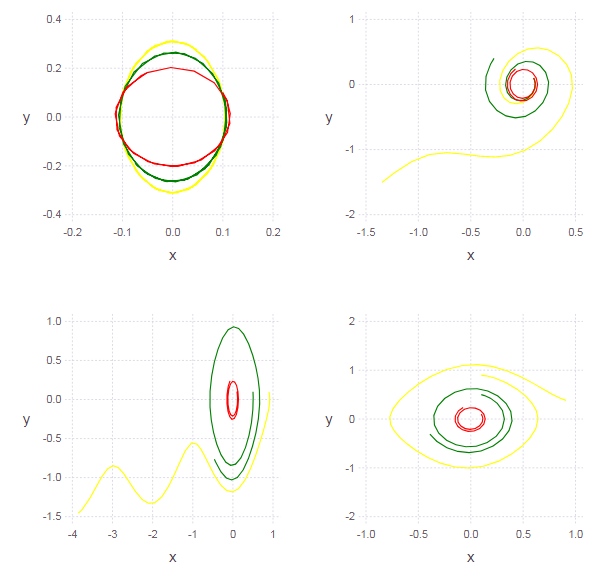
 L = Array{Any}(undef, 3)#     (  ) clr = ["red" "green" "yellow"] function ploter(Answ) for i = 1:3 L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path, Theme(default_color=clr[i]) ) end p = plot(L[1], L[2], L[3]) end Ans1 = garmosc.( [pi 2pi 3pi] )#  p1 = ploter(Ans1) Ans2 = garmosc.( pi, [0.1 0.3 0.5] )#  p2 = ploter(Ans2) Ans3 = garmosc.( pi, 0.1, [0.2 0.5 0.8] ) p3 = ploter(Ans3) Ans4 = garmosc.( pi, 0.1, 0.1, [0.2 0.5 0.8] ) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) ) #     

الآن لا نعتبر التذبذبات الصغيرة ، ولكن التذبذبات في السعة التعسفية:

مخطط الطور للحل ليس قطعًا بيضاويًا (مما يشير إلى عدم خطية المذبذب). كلما قل اختيارنا لسعة التذبذبات (أي الشروط الأولية) ، كلما ظهر انخفاض الخطية (لذلك ، يمكن اعتبار التذبذبات الصغيرة للبندول متناسقة).

 function ungarmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) function syst(du,u,p,t) du[1] = u[2] du[2] = -sin( ω*u[1] )+γ*u[2] end u0 = [x0, y0] # start cond-ns tspan = (0.0, 2pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end Ans1 = ungarmosc.( [pi 2pi 3pi] ) p1 = ploter(Ans1) Ans2 = ungarmosc.( pi, [0.1 0.4 0.7] ) p2 = ploter(Ans2) Ans3 = ungarmosc.( pi, 0.1, [0.1 0.5 0.9] ) p3 = ploter(Ans3) Ans4 = ungarmosc.( pi, 0.1, 0.1, [0.1 0.5 0.9] ) p4 = ploter(Ans4) vstack( hstack(p1,p2), hstack(p3,p4) ) 

بروكسل

يصف هذا النموذج تفاعلًا كيميائيًا تحفيزيًا معينًا يلعب فيه الانتشار دورًا. تم اقتراح النموذج في عام 1968 من قبل Lefebvre و Prigozhin.

وظائف غير معروفة $$$u_1 (t) ، \ ، u_2 (t)$ تعكس ديناميات تركيز المنتجات الوسيطة للتفاعل الكيميائي. معلمة النموذج $$$\ mu$ إن التركيز الأولي للمحفز (المادة الثالثة) منطقي.

بمزيد من التفصيل ، يمكن ملاحظة تطور صورة الطور للمحاور عن طريق إجراء حسابات بمعلمات مختلفة $$$\ mu$ . مع زيادتها ، ستتحول العقدة أولاً تدريجيًا إلى نقطة ذات إحداثيات (1 ، $$$\ mu$ ) حتى تصل إلى قيمة التشعب $$$\ mu$ = 2. عند هذه النقطة ، هناك إعادة هيكلة نوعية للصورة ، يتم التعبير عنها في ولادة دورة الحد. مع زيادة أخرى $$$\ mu$ يحدث تغيير كمي فقط في معلمات هذه الدورة.

 function brusselator(μ = 0.1, u0 = [0.1; 0.1]) function syst(du,u,p,t) du[1] = -(μ+1)*u[1] + u[1]*u[1]*u[2] + 1 du[2] = μ*u[1] - u[1]*u[1]*u[2] end tspan = (0.0, 10) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 1) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end L = Array{Any}(undef, 10) function ploter(Answ) for i = 1:length(Answ) L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path ) end plot(L[1], L[2], L[3], L[4], L[5], L[6], L[7], L[8], L[9], L[10]) end SC = [ [0 0.5], [0 1.5], [2.5 0], [1.5 0], [0.5 1], [1 0], [1 1], [1.5 2], [0.1 0.1], [0.5 0.2] ] Ans1 = brusselator.( 0.1, SC ) Ans2 = brusselator.( 0.8, SC ) Ans3 = brusselator.( 1.6, SC ) Ans4 = brusselator.( 2.5, SC ) p1 = ploter(Ans1) p2 = ploter(Ans2) p3 = ploter(Ans3) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) ) 

يكفي اليوم. في المرة القادمة ، سنحاول معرفة كيفية استخدام حزمة رسومات أخرى للمهام الجديدة ، بينما نكتب في نفس الوقت بناء جملة جوليا. في عملية حل المشكلات ، يتم تتبعك ببطء ، وليس أن الإيجابيات والسلبيات مباشرة ... بدلاً من ذلك ، وسائل الراحة والإزعاج - يجب تخصيص محادثة منفصلة لذلك. وبالطبع ، أود أن أرى شيئًا أكثر خطورة على هبري من ألعابي ذات الوظائف - لذلك ، أحث علماء القانون على إخبار المزيد عن المشاريع الأكثر جدية ، وهذا سيساعد الكثيرين ، وعلى وجه الخصوص ، في تعلم هذه اللغة الرائعة.