يعد التشفير التلقائي المتغير (التشفير التلقائي) نموذجًا توليديًا يتعلم عرض الكائنات في مساحة مخفية معينة.

هل تساءلت يومًا عن كيفية عمل نموذج التشفير التلقائي المتغير (VAE)؟ هل تريد أن تعرف كيف يولد VAE أمثلة جديدة مثل مجموعة البيانات التي تم تدريبها عليها؟ بعد قراءة هذا المقال ، ستحصل على فهم نظري للعمل الداخلي لـ VAE ، ويمكنك أيضًا تنفيذه بنفسك. ثم سأعرض كود VAE العامل المدرب على مجموعة من الأرقام المكتوبة بخط اليد ، وسوف نحصل على بعض المرح ، ننتج أرقامًا جديدة!

نماذج مولدة

VAE هو نموذج تولد - فهو يقدر كثافة الاحتمال (PDF) لبيانات التدريب. إذا تم تدريب هذا النموذج على الصور الطبيعية ، فسوف يعين قيمة احتمالية عالية لصورة الأسد ، وقيمة منخفضة لصورة الهراء العشوائي.

يعرف طراز VAE أيضًا كيفية أخذ أمثلة من ملف PDF مدرب ، وهو أروع جزء ، حيث يمكن أن يولد أمثلة جديدة مشابهة لمجموعة البيانات الأصلية!

سأشرح VAE باستخدام مجموعة MNIST المكتوبة بخط اليد. البيانات المدخلة للنموذج هي صور بتنسيق $$$\ mathbb {R} ^ {28 × 28}$ . يجب أن يقيّم النموذج احتمالية مقدار المدخلات التي تبدو مثل رقم.

مهمة نمذجة الصورة

التفاعل بين البكسل مهمة صعبة. إذا كانت وحدات البكسل مستقلة عن بعضها البعض ، فأنت بحاجة إلى دراسة ملف PDF لكل بكسل بشكل مستقل ، وهو أمر سهل. التحديد بسيط أيضًا - نأخذ كل بكسل على حدة.

ولكن في الصور الرقمية ، هناك تبعيات واضحة بين وحدات البكسل. إذا رأيت بداية الأربعة على النصف الأيسر ، فستفاجأ جدًا إذا كان النصف الأيمن هو الانتهاء من الصفر. لكن لماذا؟ ..

المساحة المخفية

أنت تعلم أن كل صورة لها رقم واحد. مدخل $$$\ mathbb {R} ^ {28 × 28}$ من الواضح أنها لا تحتوي على هذه المعلومات. ولكن يجب أن يكون في مكان ما ... هذه "في مكان ما" هي مساحة مخفية.



يمكنك التفكير في الفضاء الخفي مثل $$$\ mathbb {R} ^ {k}$ حيث يحتوي كل متجه $$$k$ قطعة من المعلومات اللازمة لتقديم صورة. افترض أن البعد الأول يحتوي على رقم يمثله رقم. البعد الثاني قد يكون العرض. والثالث هو الزاوية ، وهكذا.

يمكننا أن نتصور عملية رسم شخص في خطوتين. أولاً ، يحدد الشخص - بوعي أم لا - جميع سمات الرقم الذي سيتم عرضه. بعد ذلك ، يتم تحويل هذه القرارات إلى ضربات على الورق.

يحاول VAE محاكاة هذه العملية: لصورة معينة $$$x$ نريد أن نجد متجهًا مخفيًا واحدًا على الأقل يمكنه وصفه ؛ ناقل واحد يحتوي على تعليمات للتوليد $$$x$ . ومن خلال صياغتها بصيغة الاحتمال الكلي ، نحصل عليها $$$P (x) = \ int P (x | z) P (z) dz$ .

دعونا نضع بعض المعقول في هذه المعادلة:

• يعني التكامل أنه يجب البحث عن المرشحين في جميع الأماكن المخفية.
• لكل مرشح $$$z$ نسأل السؤال: هل من الممكن أن تولد $$$x$ باستخدام التعليمات $$$z$ ؟؟؟ هل هي كبيرة بما يكفي $$$P (x | z)$ ؟؟؟ على سبيل المثال ، إذا $$$z$ يشفر معلومات حول الرقم 7 ، ثم الصورة 8 غير ممكنة. ومع ذلك ، فإن الصورة 1 مقبولة لأن 1 و 7 متشابهان.
• وجدنا واحدة جيدة. $$$z$ ؟؟؟ عظيم! ولكن انتظر ثانية ... كم هو $$$z$ ربما؟ $$$P (z)$ كبيرة بما يكفي؟ ضع في اعتبارك صورة الرقم المقلوب 7. وستكون المطابقة المثالية متجهًا مخفيًا يصف العرض 7 ، حيث يتم تعيين حجم الزاوية على 180 درجة. ولكن مثل هذا $$$z$ من غير المحتمل ، لأن الأرقام عادة لا تكتب بزاوية 180 درجة.

الهدف من تدريب VAE هو تعظيم $$$P (x)$ . سنقوم النموذج $$$P (x | z)$ باستخدام التوزيع الغوسي متعدد الأبعاد $$$\ mathcal {N} (f (z)، \ sigma ^ 2 \ cdot I)$ .

$$$f (z)$ على غرار شبكة عصبية. $$$\ سيجما$ هي معلمة مفرطة لضرب مصفوفة الهوية $$$I$ .

ضع في اعتبارك أن $$$f$ - هذا ما سنستخدمه لإنشاء صور جديدة باستخدام نموذج مدرب. تداخل التوزيع الغوسي للأغراض التعليمية فقط. إذا أخذنا وظيفة Dirac delta (أي حتمية $$$x = f (z)$ ) ، فلن نتمكن من تدريب النموذج باستخدام منحدر التدرج!

عجائب الفضاء الخفي

نهج الفضاء الخفي يواجه مشكلتين كبيرتين:

1. ما المعلومات التي يحتوي عليها كل بُعد؟ قد تتعلق بعض الأبعاد بعناصر مجردة ، مثل النمط. حتى إذا كان من السهل تفسير جميع الأبعاد ، فإننا لا نريد تعيين تصنيفات لمجموعة البيانات. هذا النهج لا يتغير إلى مجموعات البيانات الأخرى.
2. يمكن الخلط بين الفضاء المخفي عندما يكون هناك ارتباط بين الأبعاد. على سبيل المثال ، يمكن أن يؤدي الرقم الذي يتم رسمه بسرعة كبيرة في وقت واحد إلى ظهور ضربات زوايا ورقيقة. تحديد هذه التبعيات أمر صعب.

يأتي التعلم العميق لإنقاذ

اتضح أنه يمكن إنشاء كل توزيع من خلال تطبيق دالة معقدة إلى حد ما على التوزيع الغوسي القياسي متعدد الأبعاد.

اختر $$$P (z)$ كتوزيع غوسي قياسي متعدد الأبعاد. وهكذا تم تصميمه بواسطة شبكة عصبية $$$f$ يمكن تقسيمها إلى مرحلتين:

1. الطبقات الأولى تحدد التوزيع الغوسي في التوزيع الحقيقي على المساحة المخفية. لا يمكننا تفسير القياسات ، لكن هذا لا يهم.
2. سيتم عرض الطبقات اللاحقة من المساحة المخفية في $$$P (x | z)$ .

فكيف ندرب هذا الوحش؟

صيغة ل $$$P (x)$ لذلك ، نحن غير تقريبيين بطريقة مونت كارلو:

1. الاختيار $$$\ {z_i \} _ {i = 1} ^ n$ من السابق $$$P (z)$
2. التقريب مع $$$P (x) \ تقريبا \ frac {1} {n} \ sum_ {i = 1} ^ n P (x | z_i)$

عظيم! لذلك فقط حاول الكثير من مختلف $$$z$ وابدأ حفل نشر الخلل!

لسوء الحظ منذ ذلك الحين $$$x$ متعدد الأبعاد للغاية ، للحصول على تقريب معقول ، هناك حاجة إلى العديد من العينات. أعني إذا حاولت $$$z$ ثم ما هي فرص الحصول على صورة تبدو مثل شيء $$$x$ ؟؟؟ هذا ، بالمناسبة ، يفسر السبب $$$P (x | z)$ يجب تعيين قيمة احتمالية إيجابية لأي صورة محتملة ، وإلا لن يتمكن النموذج من التعلم: أخذ العينات $$$z$ ستؤدي إلى صورة مختلفة تقريبًا عن $$$x$ ، وإذا كان الاحتمال يساوي 0 ، فلن يتمكن التدرج من الانتشار.

كيف تحل هذه المشكلة؟

قطع الطريق!

معظم العينات $$$z$ لن يتم إضافة أي شيء من التحديد إلى $$$P (x)$ - إنهم بعيدون جدا عن حدودها. الآن ، إذا كنت تعرف مقدمًا إلى أين تأخذهم من ...

يمكن الدخول $$$Q (z | x)$ . تعطى $$$Q$ سيتم تدريبهم على تعيين قيم احتمالية عالية لـ $$$z$ التي من المحتمل أن تولد $$$x$ . الآن يمكنك إجراء تقييم باستخدام طريقة مونت كارلو ، مع أخذ عينات أقل بكثير من $$$Q$ .

لسوء الحظ ، تنشأ مشكلة جديدة! بدلا من تعظيم $$$P (x) = \ int P (x | z) P (z) dz = \ mathbb {E} _ {z \ sim P (z)} P (x | z)$ نحن تكبير $$$\ mathbb {E} _ {z \ sim Q (z | x)} P (x | z)$ . كيف ترتبط ببعضها البعض؟

الاستنتاج المتغير

الخلاصة المتغيرة هي موضوع مقال منفصل ، لذلك لن أتناولها هنا بالتفصيل. أستطيع أن أقول فقط أن هذه التوزيعات مرتبطة بهذه المعادلة:

$$

$$log P (X) - \ mathcal {KL} [Q (z | x) || P (z | x)] = \ mathbb {E} _ {z \ sim Q (z | x)} [log P (x | z)] - \ mathcal {KL} [Q (z | x) || P (ض)]$$

$$$\ mathcal {KL}$ هي مسافة Kullback - Leibler ، التي تقيم بشكل حدسي التشابه بين التوزيعين.

في لحظة ، سترى كيفية تكبير الجانب الأيمن من المعادلة. في هذه الحالة ، يتم تكبير الجانب الأيسر أيضًا:

• $$$P (x)$ إلى أقصى حد.
• إلى أي مدى $$$Q (z | x)$ من $$$P (z | x)$ - حقيقي بداهة غير معروف - سيتم تصغيره.

معنى الجانب الأيمن من المعادلة هو أن لدينا توتر هنا:

1. من ناحية ، نريد زيادة مدى نجاحها $$$x$ يجب فك الشفرة من $$$z \ sim Q$ .
2. من ناحية أخرى ، نريد $$$Q (z | x)$ ( التشفير ) كان مشابهًا لما سبق $$$P (z)$ (توزيع غوسي متعدد الأبعاد). هذا يمكن اعتباره تسوية.

التقليل من الاختلاف $$$\ mathcal {KL}$ تتم بسهولة مع الاختيار الصحيح للتوزيعات. سنقوم بالمحاكاة $$$Q (z | x)$ كشبكة عصبية ، ومخرجاتها هي معلمات توزيع غوسي متعدد الأبعاد:

• متوسط $$$\ mu_Q$
• مصفوفة التغاير القطري $$$\ Sigma_Q$

ثم الاختلاف $$$\ mathcal {KL}$ يصبح قابل للحل التحليلي ، وهو أمر رائع بالنسبة لنا (وللتدرجات).

جزء وحدة فك التشفير أكثر تعقيدًا بعض الشيء. للوهلة الأولى ، أود أن أذكر أن هذه المشكلة غير قابلة للحل بطريقة مونت كارلو. لكن العينة $$$z$ من $$$Q$ لن يسمح للتدرجات بالانتشار من خلال $$$Q$ ، لأن التحديد ليس عملية مختلفة. هذه مشكلة ، منذ ذلك الحين أوزان إصدار الطبقات $$$\ Sigma_Q$ و $$$\ mu_Q$ .

خدعة معلمات جديدة

يمكننا استبداله $$$Q$ التحول المحدد القطعي لمتغير عشوائي غير معلمي:

1. عينة من التوزيع الغوسي القياسي (بدون معلمات).
2. ضرب العينة في الجذر التربيعي $$$\ Sigma_Q$ .
3. إضافة إلى النتيجة $$$\ mu_Q$ .

نتيجة لذلك ، نحصل على توزيع يساوي $$$Q$ . الآن تأتي عملية الجلب من التوزيع الغوسي القياسي. وبالتالي ، يمكن أن تنتشر التدرجات من خلال $$$\ Sigma_Q$ و $$$\ mu_Q$ منذ الآن هذه مسارات حتمية.

النتيجة؟ سيكون النموذج قادرًا على معرفة كيفية ضبط المعلمات $$$Q$ : سوف تركز على الخير $$$z$ القادرة على الإنتاج $$$x$ .

ضع كل ذلك معًا

قد يكون من الصعب فهم طراز VAE. لقد درسنا هنا الكثير من المواد التي يصعب هضمها.

دعني ألخص كل خطوات تطبيق VAE.



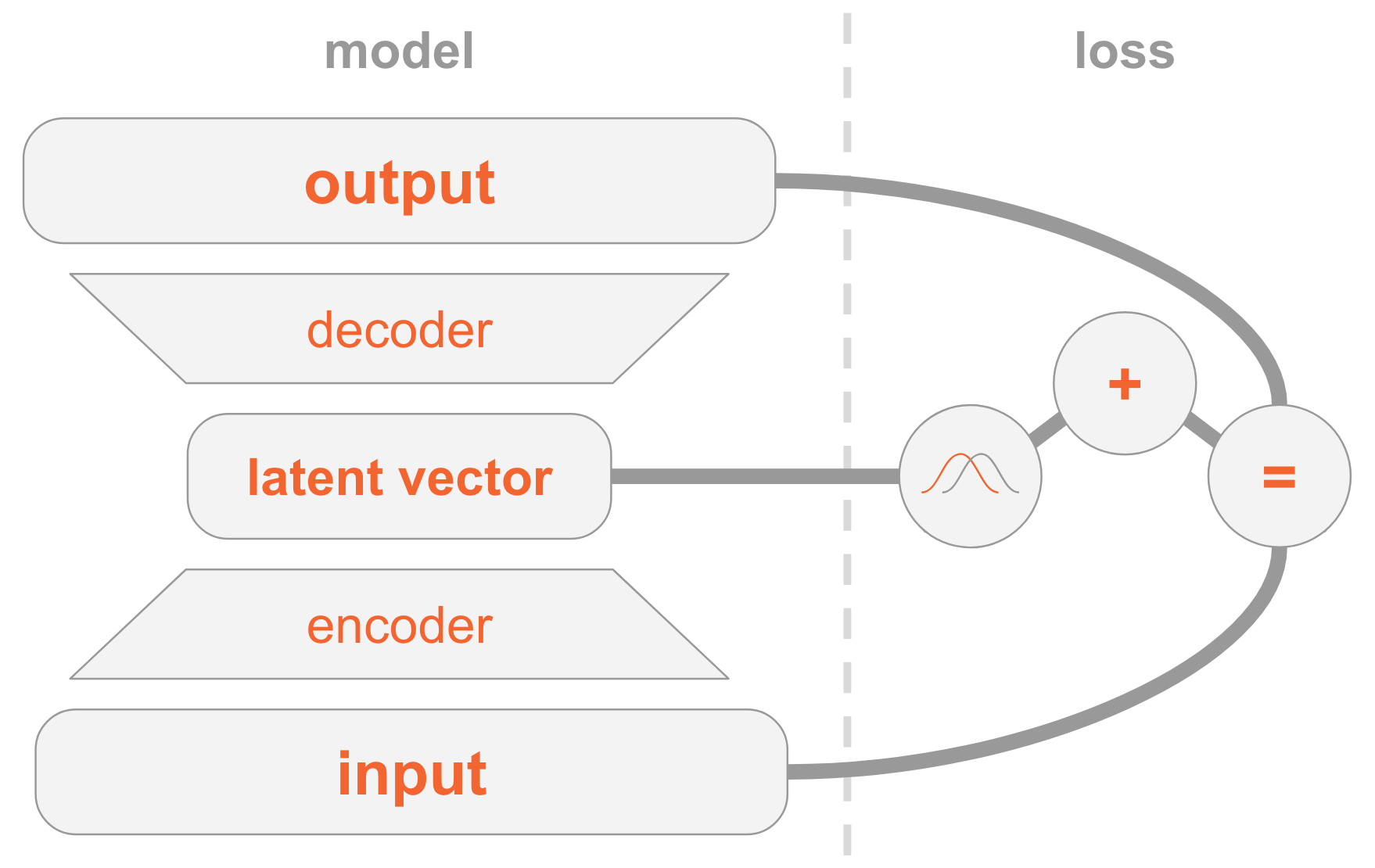
على اليسار لدينا تعريف نموذج:

1. يتم إرسال صورة الإدخال من خلال شبكة التشفير.
2. يوفر التشفير معلمات التوزيع $$$Q (z | x)$ .
3. ناقل مخفي $$$z$ مأخوذة من $$$Q (z | x)$ . إذا كان برنامج التشفير مدربًا بشكل جيد ، في معظم الحالات $$$z$ تحتوي على وصف $$$x$ .
4. فك رموز فك $$$z$ في الصورة.

على الجانب الأيمن ، لدينا وظيفة الخسارة:

1. خطأ في الاسترداد: يجب أن يكون الإخراج مشابهًا للإدخال.
2. $$$Q (z | x)$ يجب أن يكون مشابهًا للتوزيع السابق ، أي التوزيع العادي القياسي متعدد الأبعاد.

لإنشاء صور جديدة ، يمكنك تحديد المتجه المخفي مباشرة من التوزيع السابق وفك تشفيره في صورة.

كود العمل

الآن سندرس VAE بمزيد من التفصيل وننظر في رمز العمل. سوف تفهم جميع التفاصيل الفنية اللازمة لتنفيذ VAE. كمكافأة ، سأوضح لك خدعة مثيرة للاهتمام: كيفية تعيين أدوار خاصة لبعض أبعاد المتجه المخفي حتى يبدأ النموذج في إنشاء صور للأرقام المشار إليها.

import numpy as np import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt np.random.seed(42) tf.set_random_seed(42) %matplotlib inline 

أذكركم أن النماذج مدربة على MNIST - مجموعة من الأرقام المكتوبة بخط اليد. تأتي الصور المدخلة بالتنسيق $$$\ mathbb {R} ^ {28 × 28}$ .

 mnist = input_data.read_data_sets('MNIST_data') input_size = 28 * 28 num_digits = 10 

بعد ذلك ، نحدد المعايير الفائقة.

لا تتردد في اللعب بقيم مختلفة للحصول على فكرة عن كيفية تأثيرها على النموذج.

 params = { 'encoder_layers': [128], #       'decoder_layers': [128], #    (CNN ,     ) 'digit_classification_layers': [128], #   ,   'activation': tf.nn.sigmoid, #      'decoder_std': 0.5, #   P(x|z)   'z_dim': 10, #    'digit_classification_weight': 10.0, #   ,   'epochs': 20, 'batch_size': 100, 'learning_rate': 0.001 } 

نموذج

يتكون النموذج من ثلاث شبكات فرعية:

1. يحصل $$$x$ (صورة) ، ترمز إلى توزيع $$$Q (z | x)$ في الفضاء الخفي.
2. يحصل $$$z$ في الفضاء الخفي (تمثيل الرمز للصورة) ، يفك تشفيرها في الصورة المقابلة $$$f (z)$ .
3. يحصل $$$x$ ويحدد الرقم من خلال المقارنة مع الطبقة ذات الأبعاد العشرة ، حيث تحتوي القيمة من الأول إلى احتمال الرقم من الأول.

أول شبكتين فرعيتين هي أساس VAE النقي.

والثالثة هي مهمة مساعدة تستخدم بعض الأبعاد المخفية لترميز الأرقام الموجودة في الصورة. سأشرح السبب: ناقشنا في وقت سابق أننا لا نهتم بالمعلومات التي يحتوي عليها كل بُعد من المساحة المخفية. يمكن أن يتعلم النموذج ترميز أي معلومات يعتبرها ذات قيمة لمهمته. نظرًا لأننا على دراية بمجموعة البيانات ، فإننا نعلم أهمية البعد ، الذي يحتوي على نوع الرقم (أي قيمته العددية). والآن نريد مساعدة النموذج من خلال تزويدها بهذه المعلومات.

بالنسبة إلى نوع معين من الأرقام ، نقوم بترميزه مباشرة ، أي أننا نستخدم متجهًا بالحجم 10. ترتبط هذه الأرقام العشرة بمتجه مخفي ، لذلك عند فك تشفير هذا المتجه إلى صورة ، سيستخدم النموذج المعلومات الرقمية.

هناك طريقتان لتوفير نماذج ناقلات الترميز المباشر:

1. أضفه كمدخل للنموذج.
2. قم بإضافته كتسمية ، بحيث يقوم النموذج نفسه بحساب التوقعات: سنضيف شبكة فرعية أخرى تتنبأ بمتجه 10 أبعاد ، حيث تكون وظيفة الخسارة هي الكون المتقاطع مع متجه الترميز الأمامي المتوقع.

حدد الخيار الثاني. لماذا؟ حسنًا ، عند الاختبار ، يمكنك استخدام النموذج بطريقتين:

1. حدد الصورة كمدخل وعرض متجه مخفي.
2. حدد متجهًا مخفيًا كإدخال وقم بإنشاء صورة.

نظرًا لأننا نريد دعم الخيار الأول ، لا يمكننا إعطاء النموذج رقمًا كمدخل ، لأننا لا نريد أن نعرفه أثناء الاختبار. لذلك ، يجب أن يتعلم النموذج التنبؤ به.

 def encoder(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) mu = tf.layers.dense(x, params['z_dim']) var = 1e-5 + tf.exp(tf.layers.dense(x, params['z_dim'])) return mu, var def decoder(z, layers): for layer in layers: z = tf.layers.dense(z, layer, activation=params['activation']) mu = tf.layers.dense(z, input_size) return tf.nn.sigmoid(mu) def digit_classifier(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) logits = tf.layers.dense(x, num_digits) return logits 

 images = tf.placeholder(tf.float32, [None, input_size]) digits = tf.placeholder(tf.int32, [None]) #        encoder_mu, encoder_var = encoder(images, params['encoder_layers']) #     ,  #     eps = tf.random_normal(shape=[tf.shape(images)[0], params['z_dim']], mean=0.0, stddev=1.0) z = encoder_mu + tf.sqrt(encoder_var) * eps # classify the digit digit_logits = digit_classifier(images, params['digit_classification_layers']) digit_prob = tf.nn.softmax(digit_logits) #     ,  #    decoded_images = decoder(tf.concat([z, digit_prob], axis=1), params['decoder_layers']) 

 #    ,    #    loss_reconstruction = -tf.reduce_sum( tf.contrib.distributions.Normal( decoded_images, params['decoder_std'] ).log_prob(images), axis=1 ) #         . #      , #         #  ,  KL-   # ,    loss_prior = -0.5 * tf.reduce_sum( 1 + tf.log(encoder_var) - encoder_mu ** 2 - encoder_var, axis=1 ) loss_auto_encode = tf.reduce_mean( loss_reconstruction + loss_prior, axis=0 ) # digit_classification_weight      , #      loss_digit_classifier = params['digit_classification_weight'] * tf.reduce_mean( tf.nn.sparse_softmax_cross_entropy_with_logits(labels=digits, logits=digit_logits), axis=0 ) loss = loss_auto_encode + loss_digit_classifier train_op = tf.train.AdamOptimizer(params['learning_rate']).minimize(loss) 

تدريب

سوف نقوم بتدريب نموذج لتحسين وظيفتي الخسارة - VAE والتصنيف - باستخدام SGD .

في نهاية كل عصر ، نختار المتجهات المخفية ونقوم بفك تشفيرها في صور لمراقبة بصرية كيف تتحسن القوة التوليدية للنموذج على العصور. طريقة أخذ العينات هي كما يلي:

1. حدد الأبعاد التي يتم تصنيفها حسب الرقم الذي نريد إنشاؤه بشكل صريح. على سبيل المثال ، إذا أردنا إنشاء صورة للرقم 2 ، فإننا نعين القياسات $$$[0010000000]$ .
2. اختر عشوائيًا من الأبعاد الأخرى للتوزيع العادي متعدد الأبعاد. هذه هي القيم للأرقام المختلفة التي تم إنشاؤها في هذه الحقبة. لذلك لدينا فكرة عما يتم ترميزه في أبعاد أخرى ، على سبيل المثال ، أسلوب الكتابة اليدوية.

معنى الخطوة 1 هو أنه بعد التقارب ، يجب أن يكون النموذج قادرًا على تصنيف الشكل في صورة الإدخال من خلال إعدادات القياس هذه. ومع ذلك ، يتم استخدامها أيضًا في مرحلة فك التشفير لإنشاء صورة. بمعنى ، تعرف الشبكة الفرعية لمفكك الشفرة: عندما تتوافق القياسات مع الرقم 2 ، يجب أن تولد صورة بهذا الرقم. لذلك ، إذا قمنا بتعيين القياسات يدويًا على الرقم 2 ، فسوف نحصل على صورة تم إنشاؤها لهذا الرقم.

 samples = [] losses_auto_encode = [] losses_digit_classifier = [] with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for epoch in xrange(params['epochs']): for _ in xrange(mnist.train.num_examples / params['batch_size']): batch_images, batch_digits = mnist.train.next_batch(params['batch_size']) sess.run(train_op, feed_dict={images: batch_images, digits: batch_digits}) train_loss_auto_encode, train_loss_digit_classifier = sess.run( [loss_auto_encode, loss_digit_classifier], {images: mnist.train.images, digits: mnist.train.labels}) losses_auto_encode.append(train_loss_auto_encode) losses_digit_classifier.append(train_loss_digit_classifier) sample_z = np.tile(np.random.randn(1, params['z_dim']), reps=[num_digits, 1]) gen_samples = sess.run(decoded_images, feed_dict={z: sample_z, digit_prob: np.eye(num_digits)}) samples.append(gen_samples) 

دعونا نتحقق من أن وظيفتي الخسارة تبدو جيدة ، أي أنها تقل:

 plt.subplot(121) plt.plot(losses_auto_encode) plt.title('VAE loss') plt.subplot(122) plt.plot(losses_digit_classifier) plt.title('digit classifier loss') plt.tight_layout() 

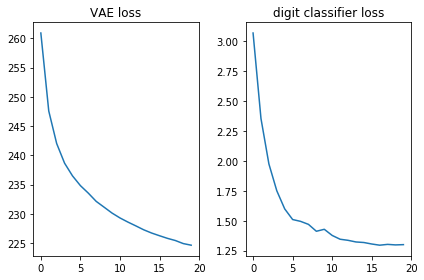
بالإضافة إلى ذلك ، دعنا نعرض الصور التي تم إنشاؤها ونرى ما إذا كان بإمكان النموذج حقًا إنشاء صور بأرقام مكتوبة بخط اليد:

 def plot_samples(samples): IMAGE_WIDTH = 0.7 plt.figure(figsize=(IMAGE_WIDTH * num_digits, len(samples) * IMAGE_WIDTH)) for epoch, images in enumerate(samples): for digit, image in enumerate(images): plt.subplot(len(samples), num_digits, epoch * num_digits + digit + 1) plt.imshow(image.reshape((28, 28)), cmap='Greys_r') plt.gca().xaxis.set_visible(False) if digit == 0: plt.gca().yaxis.set_ticks([]) plt.ylabel('epoch {}'.format(epoch + 1), verticalalignment='center', horizontalalignment='right', rotation=0, fontsize=14) else: plt.gca().yaxis.set_visible(False) plot_samples(samples) 

الخلاصة

من الجميل أن نرى أن شبكة التوزيع المباشر البسيطة (بدون التواءات فاخرة) تولد صورًا جميلة في 20 حقبة فقط. تعلم النموذج بسرعة استخدام قياسات خاصة للأرقام: في العصر التاسع ، رأينا بالفعل تسلسل الأرقام التي كنا نحاول توليدها.

استخدمت كل حقبة قيمًا عشوائية مختلفة لأبعاد أخرى ، لذلك يختلف النمط بين العصور ، لكنه متشابه داخلها: على الأقل داخل البعض. على سبيل المثال ، في الثامن عشر ، تكون جميع الأرقام أكثر بدانة مقارنةً بالعدد 20.

ملاحظات

تعتمد المقالة على تجربتي والمصادر التالية:

• الاستنتاج المتغير والتعلم العميق: تركيب جديد
• اختلاف دليل المبرمج التلقائي