دورة معهد ماساتشوستس للتكنولوجيا "أمن أنظمة الكمبيوتر". المحاضرة 16: "هجمات القناة الجانبية" ، الجزء الأول

معهد ماساتشوستس للتكنولوجيا. محاضرة رقم 6.858. "أمن أنظمة الكمبيوتر." نيكولاي زيلدوفيتش ، جيمس ميكنز. 2014 سنة

أمان أنظمة الكمبيوتر هي دورة حول تطوير وتنفيذ أنظمة الكمبيوتر الآمنة. تغطي المحاضرات نماذج التهديد ، والهجمات التي تهدد الأمن ، وتقنيات الأمان بناءً على العمل العلمي الحديث. تشمل الموضوعات أمان نظام التشغيل (OS) ، والميزات ، وإدارة تدفق المعلومات ، وأمان اللغة ، وبروتوكولات الشبكة ، وأمان الأجهزة ، وأمان تطبيقات الويب.

المحاضرة 1: "مقدمة: نماذج التهديد" الجزء 1 / الجزء 2 / الجزء 3
المحاضرة 2: "السيطرة على هجمات القراصنة" الجزء 1 / الجزء 2 / الجزء 3
المحاضرة 3: "تجاوزات العازلة: المآثر والحماية" الجزء 1 / الجزء 2 / الجزء 3
المحاضرة 4: "فصل الامتيازات" الجزء 1 / الجزء 2 / الجزء 3
المحاضرة 5: "من أين تأتي أنظمة الأمن؟" الجزء 1 / الجزء 2
المحاضرة 6: "الفرص" الجزء 1 / الجزء 2 / الجزء 3
المحاضرة 7: "وضع حماية العميل الأصلي" الجزء 1 / الجزء 2 / الجزء 3
المحاضرة 8: "نموذج أمن الشبكات" الجزء 1 / الجزء 2 / الجزء 3
المحاضرة 9: "أمان تطبيق الويب" الجزء 1 / الجزء 2 / الجزء 3
المحاضرة 10: "التنفيذ الرمزي" الجزء 1 / الجزء 2 / الجزء 3
المحاضرة 11: "لغة برمجة Ur / Web" الجزء 1 / الجزء 2 / الجزء 3
المحاضرة 12: أمن الشبكات الجزء 1 / الجزء 2 / الجزء 3
المحاضرة 13: "بروتوكولات الشبكة" الجزء 1 / الجزء 2 / الجزء 3
المحاضرة 14: "SSL و HTTPS" الجزء 1 / الجزء 2 / الجزء 3
المحاضرة 15: "البرامج الطبية" الجزء 1 / الجزء 2 / الجزء 3
المحاضرة 16: "هجمات القناة الجانبية" الجزء 1 / الجزء 2 / الجزء 3

حسنًا يا رفاق ، فلنبدأ. لذلك ، سنتحدث اليوم عن الهجمات عبر القنوات الجانبية ، وهي مشكلة شائعة متأصلة في جميع أنواع الأنظمة. بشكل عام ، تحدث الهجمات عبر القناة الجانبية في موقف لا تعتقد فيه أن بعض المعلومات قادرة على الكشف عن معلومات حول نظامك.



عادةً ، لديك العديد من المكونات التي تنشئ اتصالاً بين المستخدم والخادم. في الوقت نفسه ، تعتقد أنك تعرف كل شيء يمر عبر هذا السلك الذي يربط بين مشتركين ، وتعلم كل البتات التي يتبادلها المستخدم والخادم مع بعضها البعض ، وهذا آمن. ولكن غالبًا ما يحدث أن المستخدم أو الخادم لا يزال يفصح عن بعض المعلومات. يصف المثال الموضح في محاضرة اليوم حالة حيث تكشف مزامنة الرسائل بين المستخدم والخادم بعض المعلومات الإضافية التي لا تعرفها ، فقط من خلال مراقبة تدفق البت بين هؤلاء المشتركين.

في الواقع ، هناك فئة أوسع بكثير من القنوات الجانبية التي يمكن أن تقلق بشأنها. تعلم الناس عن ظهور القنوات الجانبية في الأربعينيات ، عندما اكتشفوا أنه إذا بدأت في كتابة الأحرف على teletype ، فستبدأ إلكترونيات teletype في إصدار إشعاع التردد اللاسلكي. في هذه الحالة ، يمكنك ببساطة وضع مرسمة الذبذبات بجواره وملاحظة كيفية تغير تردد إشارة الراديو اعتمادًا على الرمز الذي يطبعه عامل التليفزيون. وبالتالي ، فإن إشعاع التردد اللاسلكي هو مثال كلاسيكي لقناة جانبية تجعلك تقلق.

هناك العديد من الأمثلة الأخرى التي لاحظها الناس ، مثل استهلاك الكهرباء. هذه قناة جانبية أخرى يمكن أن تقلق بشأنها ، لأن جهاز الكمبيوتر الخاص بك سيستخدم كمية مختلفة من الطاقة اعتمادًا على ما يحسبه.



مثال على القناة الجانبية هو الصوت ، والذي من الممكن أيضًا حدوث تسرب للمعلومات. على سبيل المثال ، يستمع الأشخاص إلى الطابعة ، واستنادًا إلى الأصوات التي يصدرونها ، يمكنهم معرفة الأحرف التي تطبعها. يعد ذلك أمرًا سهلاً بشكل خاص لطابعات المصفوفة التي تنتج أصواتًا مزعجة للغاية أثناء الطباعة.

بشكل عام ، هذا شيء يجب التفكير فيه. في محاضرة يوم الاثنين ، ذكر كيفن أيضًا بعض القنوات الجانبية المثيرة للاهتمام التي يتعامل معها في بحثه. لكننا سنلقي نظرة على القناة الجانبية المحددة التي درسها ديفيد براملي ودان بون. في عملهم ، المنشور منذ حوالي 10 سنوات ، يكتبون أنهم كانوا قادرين على استخراج مفتاح التشفير لخادم الويب Apache من خلال قياس توقيت الاستجابات المختلفة لحزم الإدخال المختلفة لعميل معاد. في هذه الحالة بالذات ، "بحثوا" عن مفتاح تشفير. في الواقع ، تستهدف العديد من الهجمات عبر القناة الجانبية مفاتيح التشفير جزئيًا لأنه من الصعب جدًا الحصول على كمية كبيرة من البيانات من خلال هذه القناة. ومفاتيح التشفير هي واحدة من الحالات التي يتم فيها إخراج عدد صغير من البتات ، أي أنه أثناء الهجوم ، يمكن للمهاجمين استخراج حوالي 200 - 256 بت من المعلومات. ولكن بناءً على 200 بت فقط ، فإنهم قادرون على كسر مفتاح التشفير لخادم الويب هذا.

إذا كنت تحاول الدخول في نوع ما من قاعدة البيانات المليئة بأرقام الضمان الاجتماعي ، فستحتاج إلى "دمج" الكثير من المعلومات. لهذا السبب تركز معظم هجمات القنوات الجانبية على الحصول على أسرار صغيرة مثل مفاتيح التشفير أو كلمات المرور. ولكن بشكل عام ، ينطبق هذا على العديد من المواقف الأخرى.

في مواد المحاضرة تم وصف شيء رائع آخر - هذا هو أنه يمكن القيام بكل هذا عبر الشبكة. ربما أدركت أنه كان عليهم القيام بالكثير من العمل الدقيق للقبض على هذه الاختلافات الأصغر في معلومات الوقت. يختلف كل طلب يرسلونه إلى الخادم عن طلب آخر بمقدار 1-2 ميكروثانية ، وهي فترة زمنية قصيرة جدًا. لذلك ، يجب أن تكون حذرًا للغاية ، لأن شبكاتنا لا تسمح لنا بالحصول على مثل هذا الاختلاف المؤقت وتحديد أن الخادم قد عالج طلبك لمدة 1-2 ميكروثانية لفترة أطول مما ينبغي.



ونتيجة لذلك ، لم يكن من الواضح ما إذا كان يمكن تنظيم مثل هذا الهجوم في شبكة "صاخبة" للغاية ، حيث يجب فصل المعلومات المفيدة عن مستوى الضوضاء. كان هؤلاء الأشخاص من بين الأوائل الذين أظهروا أنه يمكنك حقًا القيام بذلك عبر شبكة Ethernet مع خادم في أحد طرفي الشبكة وعميل في الطرف الآخر. لقد أثبتوا أنه من الممكن بالفعل قياس هذه الاختلافات جزئيًا عن طريق حساب المتوسط ​​، وجزئيًا من خلال الحيل الأخرى.
الخطة لبقية هذه المحاضرة هي على النحو التالي - أولاً نتعمق في تفاصيل خوارزمية تشفير المفتاح العام RSA التي استخدمها هؤلاء الرجال. لن نقوم بتقييمه من وجهة نظر الأمن ، لكننا سنرى كيف يتم تنفيذه ، لأن تنفيذ الخوارزمية هو أمر حاسم لاستخدام القناة الجانبية.

قام Bramley و Bone بالتدقيق في تفاصيل التنفيذ المختلفة من أجل فهم متى تؤدي بعض الأشياء بشكل أسرع أو أبطأ. لذا نحتاج أولاً إلى معرفة كيفية تنفيذ نظام تشفير RSA ، ثم سنعود ونكتشف كيفية مهاجمة كل هذه الهياكل المتوفرة في RSA.

لنبدأ بمراجعة RSA على مستوى عال. RSA هو نظام تشفير مفتاح عام يستخدم على نطاق واسع. ذكرنا هؤلاء الرجال قبل أسبوعين عندما تحدثنا عن الشهادات. الآن سنرى كيف يعمل في الواقع.

كقاعدة عامة ، هناك 3 أشياء تحتاج إلى القلق بشأنها - هذا هو توليد المفاتيح والتشفير وفك التشفير. في RSA ، طريقة إنشاء مفتاح هي تحديد عدد صحيحين رئيسيين كبيرين ، مع الإشارة إليهما بواسطة p و q. في مقالهم ، يكتب هؤلاء الرجال عن p و q لكل منهم بحجم 512 بت. يُسمى هذا عادةً RSA 1024 بت لأن منتج هذه الأعداد الأولية هو عدد صحيح 1000 بت. في هذه الأيام ، ربما لا يكون هذا خيارًا جيدًا لحجم مفتاح RSA ، لأن كسرها مهمة سهلة نسبيًا للمهاجمين. لذا ، إذا بدت 1000 بت قبل 10 سنوات كمية معقولة ، اليوم عند بناء نظام ، يجب عليك اختيار مفتاح RSA 2000 أو 3000 أو حتى 4000 بت. لذا فإن حجم مفتاح RSA يعني حجم هذه الأعداد الأولية.

بعد ذلك ، من أجل الراحة ، سنتحدث عن الرقم n ، وهو ببساطة نتاج هذه الأعداد الأولية n = pq ، ويسمى هذا الرقم الوحدة. والآن بعد أن عرفنا كيفية إنشاء المفتاح ، أو على الأقل جزء من المفتاح ، سيتعين علينا معرفة كيفية تشفير الرسائل وفك تشفيرها.



والطريقة التي سنقوم بها بتشفير الرسائل وفك تشفيرها تعتمد على رفع قوة الأرقام المعيارية n. يبدو الأمر غريبًا بعض الشيء ، لكننا سنكتشف ذلك في غضون ثانية. لذا إذا كنت تريد تشفير الرسالة m ، فيجب عليك تحويلها إلى m ^e بواسطة mod n. قيمة e هي درجة ، في ثانية سنكتشف كيفية اختيارها. بهذه الطريقة سنقوم بتشفير الرسالة.

أي أننا نأخذ هذه الرسالة كعدد صحيح ونرفعها إلى قوة. في ثانية سنرى لماذا يعمل هذا ، ولكن في الوقت الحالي ، سنشير إلى كل هذه الرسالة المشفرة بالحرف C.

بعد ذلك ، من أجل فك تشفيرها ، يجب أن نجد أس آخر مثير للاهتمام د ، والذي يسمح لنا بأخذ الرسالة المشفرة C ، ورفعها إلى السلطة d modulo n ، ونتيجة لذلك ، احصل بطريقة سحرية على الرسالة غير المشفرة m.

لذا ، فإن المبدأ العام هو استخدام أس واحد لتشفير رسالة وأسي آخر لفك تشفيرها.



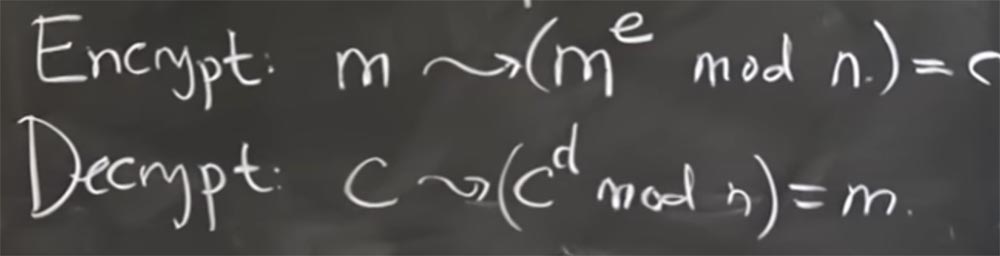
بشكل عام ، يبدو من الصعب قليلاً أن نفهم كيف سنخرج بهذين الرقمين السحريين اللذين يعيدان إلينا بطريقة ما الرسالة الأصلية. ولكن إذا نظرت إلى كيفية عمل نموذج الأسي أو الضرب هذا الرقم n ، فستفهم كل شيء.

إذا أخذنا X ورفعناها إلى قوة مساوية للدالة φ لـ n ، فسيكون هذا هو 1 وحدة n:

X ^{φ (n)} = 1 mod n

إن وظيفة phi هذه لاختيارنا الخاص لـ n بسيطة للغاية ؛ فهي تساوي φ = (p-1) (q-1).
عندئذ يكون ناتج الأس المفتوح e ، والذي يكون أكبر من 1 ولكن أقل من φ (n) ، بالمُحدد الأسري d ، مساوياً لما يلي:

ed = ɑφ (n) +1 ، حيث ɑ ثابت.

وبالتالي ، من الممكن فك تشفير الرسالة بشكل صحيح ، نظرًا لوجود خوارزمية بسيطة إلى حد ما إذا كنت تعرف قيمة φ (n) من أجل حساب d مع مراعاة e أو e مع مراعاة d.

الجمهور: هل الوحدة النمطية n لا تساوي 1؟

البروفيسور: نعم ، لقد أخطأت هنا ، والمساواة يجب أن تبدو هكذا:

X ^{φ (n)} _{mod n} = 1 mod n ، أي أن قيمة X في درجة الوظيفة "fi" من n modulo n تساوي وحدة الوحدة n.

هذا يعني في الأساس أنه بالنسبة لـ RSA ، علينا اختيار بعض القيمة الإلكترونية ، والتي ستكون قيمة التشفير لدينا. ثم من e سنقوم بإنشاء d بناءً على الصيغة de = 1 mod φ (n) ، وبالتالي d = 1 / e mod φ (n).



هناك بعض الخوارزميات الإقليدية التي يمكنك استخدامها بفعالية لهذا الحساب. ولكن من أجل القيام بذلك ، يجب أن تعرف هذا φ (n) ، والذي يتطلب عاملًا ، أي عامل الرقم n في العوامل p و q.

إذن ، RSA هو نظام حيث يكون المفتاح العام زوجًا: الأس للتشفير e والرقم n ، والزوج d و n هو مفتاح خاص يبقى سريًا. حتى يتمكن أي شخص من زيادة قوة تشفيرها لك. ولكنك فقط تعرف قيمة d وبالتالي يمكنك فك تشفير الرسالة. وحتى تعرف عامل هذه العوامل P و Q ، أو N ، تساوي ناتج P و Q ، فأنت لا تعرف ما هو φ = (p-1) (q-1).



ونتيجة لذلك ، يعد حساب قيمة d مهمة صعبة نوعًا ما. هذا ما تعنيه خوارزمية RSA عالية المستوى.

الآن بعد أن أصبحنا على دراية بمبادئ RSA ، أود أن أتناول شيئين. هناك حيل حول كيفية استخدامه بشكل صحيح وهناك مآزق تنشأ عند استخدامه. هناك العديد من الطرق لتنفيذ التعليمات البرمجية لهذا الأسي والقيام بذلك بكفاءة. هذه مهمة غير عادية إلى حد ما ، لأننا نتعامل مع أعداد صحيحة من 1000 بت ، والتي لا يمكنك فقط تنفيذ تعليمات الضرب عليها. من المحتمل أن يستغرق إكمال هذه العمليات وقتًا طويلاً.

لذلك ، أول شيء أريد أن أذكره هو المزالق المختلفة لـ RSA. أحدها هو التعددية. لنفترض أن لدينا رسالتين: m ₀ و m ₁ . سوف أقوم بتشفيرها ، مع تحويل m ₀ إلى m ₀ ^e mod n و m1 إلى m ₁ ^e mod n. مشكلة محتملة ، أو بالأحرى ، ليست بالضرورة مشكلة ، ولكن مفاجأة غير سارة لشخص يستخدم RSA هو أنه من السهل جدًا تشفير المنتج m _{0 في} m ₁ ، لأنك ببساطة تضرب هذين الرقمين: m ₀ ^e mod n * m ₁ ^e mod n.



إذا قمت بضربها ، سينتهي بك الأمر مع المنتج (m ₀ m ₁ ) ^e modulo n. هذا هو التشفير الصحيح مع الاستخدام المبسط لـ RSA للقيمة m ₀ m ₁ . هذه ليست مشكلة كبيرة في الوقت الحالي ، لأنه يمكنك ببساطة إنشاء هذه الرسالة المشفرة ، ولكن لا يمكنك فك تشفيرها. ومع ذلك ، من الممكن أن يسمح لك نظام شائع بفك تشفير رسائل معينة. أي أنه إذا كان يسمح لك بفك تشفير الرسالة التي أنشأتها ، فربما باتباع المسار العكسي ، يمكنك معرفة ما هي هذه الرسائل m ₀ و m ₁ .

لا ينبغي تجاهل هذه الحقيقة ، لأنها تؤثر على عدد من البروتوكولات باستخدام RSA. هناك خاصية واحدة سنستخدمها كآلية دفاع في نهاية محاضرتنا.

المأزق الثاني ، أو خاصية RSA ، التي يجب الانتباه إليها هو الحتمية ، أو القابلية للتحديد. في التنفيذ الأولي الموصوف سابقًا ، إذا أخذت الرسالة m وقمت بتشفيرها ، وتحويلها إلى m mod mod n ، فهذه هي وظيفة رسالة حتمية. لذلك ، إذا قمت بتشفيره مرة أخرى ، فستحصل على نفس التشفير بالضبط.

هذه ليست خاصية مرغوبة ، لأنه إذا رأيت أنك ترسل بعض الرسائل المشفرة باستخدام RSA وأريد أن أعرف ما هي ، فقد يكون من الصعب بالنسبة لي فك تشفيرها. ولكن يمكنني تجربة أشياء مختلفة ، ونتيجة لذلك أرى أنك ترسل هذه الرسالة.

ثم سأقوم بتشفيرها ومعرفة ما إذا كنت تحصل على نفس النص المشفر. وإذا كان الأمر كذلك ، فسأكتشف أنك قمت بتشفيرها. لأن كل ما أحتاجه لتشفير رسالة هو مفتاح عام يمكن الوصول إليه بشكل عام ، وهو زوج من الأرقام (n ، e).

لذلك هذا ليس رائعًا ، وقد تضطر إلى توخي الحذر في هذه الخاصية عند استخدام RSA. وبالتالي ، من الصعب استخدام البدائيين من هذا النوع مباشرة.



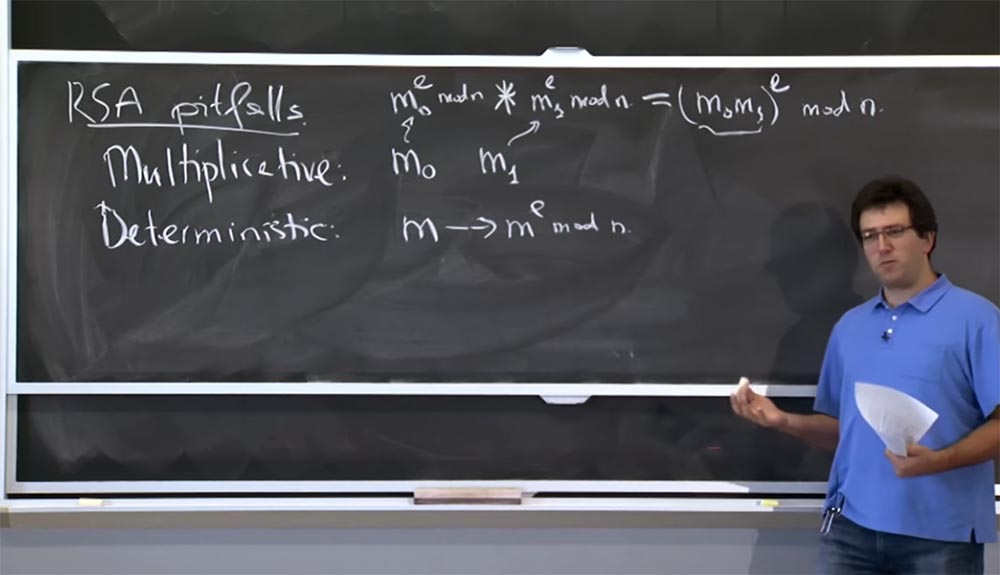
من الناحية العملية ، من أجل تجنب مشاكل مماثلة مع RSA ، يقوم الأشخاص بترميز الرسالة بطريقة معينة قبل التشفير. فبدلاً من رفع رسالة مباشرة إلى قوة ما ، فإنها تأخذ نوعًا من وظيفة الرسالة وترفعها إلى طريقة السلطة n:

(f (m)) ^e mod n.

تسمى هذه الوظيفة f ، الشائعة الاستخدام اليوم ، OAEP - التشفير غير المتماثل الأمثل مع الإضافة. هذا شيء مشفر بخاصيتين مثيرتين للاهتمام.

أولاً ، يجلب العشوائية. يمكنك التفكير في f (m) على أنها تولد رسالة 1000 بت ستقوم بتشفيرها. جزء من هذه الرسالة سيكون رسالتك m هنا في منتصف هذا المستطيل. بالطبع ، يمكنك استعادته عند فك التشفير. لذلك ، هناك شيئان مثيران للاهتمام تريد القيام به: على اليمين تضع نوعًا من العشوائية ، قيمة r. إنه يعطيك أنه إذا قمت بتشفير رسالة عدة مرات ، فستحصل على نتائج مختلفة في كل مرة ، لذلك لن يتم تحديد التشفير بعد ذلك.

من أجل التغلب على هذه الخاصية التكاثرية وأنواع أخرى من المشاكل ، على اليسار لديك وسادة ، وهي سلسلة من النوع 1 0 1 0 1 0. يمكنك اختيار تسلسل أفضل ، ولكن تقريبًا ، هذا نوع من التسلسل المتوقع ، والذي تقوم بإدراج هنا وكلما قمت بفك تشفير الرسالة ، تأكد من أن هذا التسلسل لا يزال موجودًا. سوف يؤدي التعددية إلى تدمير قطع البتات هذه ، ومن ثم سيتضح لك أن شخصًا ما قد أفسد رسالتك وتجاهلها. إذا بقيت هذه البتات في مكانها ، فهذا يثبت أنه لم يقم أحد بتزوير رسالتك وأنك قادر على استلامها ، حيث تم تشفيرها بشكل صحيح من قبل شخص ما.



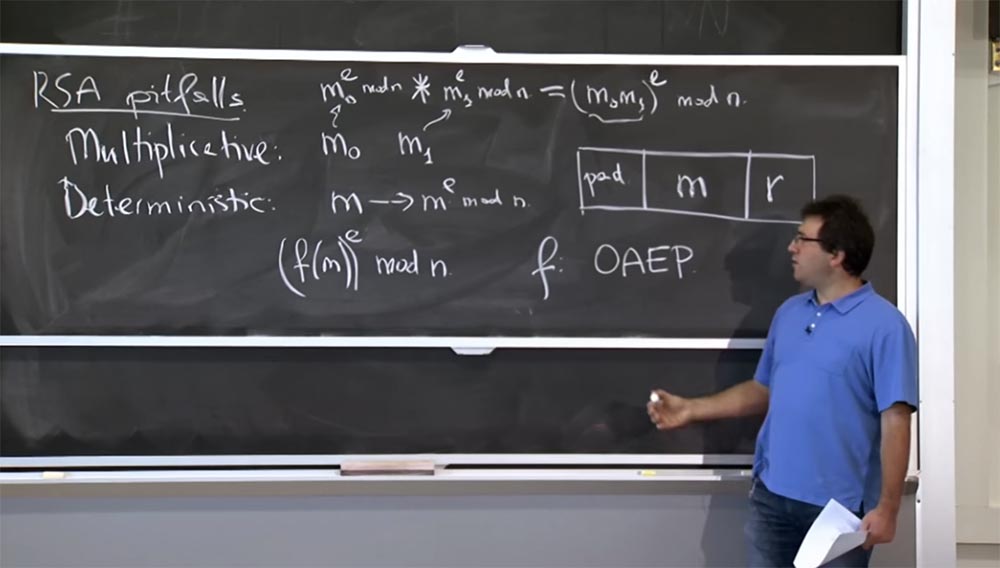الجمهور: إذا كان المهاجم يعرف كم تبلغ قيمة الوسادة ، فهل يمكنه تعيين 1 في أسفل التسلسل ثم مضاعفة هذه القيمة؟

الأستاذ: نعم ، ربما. هذا معقد بعض الشيء ، لأن هذه العشوائية ستستمر. لذا فإن التصميم المحدد لـ OAEP أكثر تعقيدًا قليلاً مما تصورته. ولكن تخيل أن هذا هو عدد صحيح بدلاً من الضرب على شكل بت ، فالعشوائية تمتد إلى أبعد من ذلك ، لذا يمكنك إنشاء مخطط OAEP لن يحدث فيه ذلك.

اتضح أنه لا يجب عليك استخدام رياضيات RSA هذه مباشرة ، عمليًا ، يجب عليك استخدام مكتبة معينة تقوم بتنفيذ كل هذه الأشياء لك بالطريقة الصحيحة ، واستخدامها كمعلمة تشفير وفك تشفير.

ومع ذلك ، فإن التفاصيل التي نوقشت أعلاه ستكون ذات قيمة بالنسبة لنا ، لأننا نحاول في الواقع معرفة كيفية كسر أو مهاجمة تنفيذ RSA الحالي.

على وجه الخصوص ، سوف يستفيد الهجوم الموصوف في مقالة المحاضرة من حقيقة أن الخادم على وشك اختبار وظيفة الضبط الإضافية هذه عندما يتلقى الرسالة. هذه هي الطريقة التي سنأخذ بها في الاعتبار الوقت الذي يستغرقه الخادم لفك التشفير. سنقوم بإرسال رسالة تم إنشاؤها بعناية ، ولكن لم يتم إنشاؤها من الرسالة الحقيقية m وتشفيرها. سنقوم بإنشاء قيمة صحيحة مشفرة.

سيحاول الخادم فك تشفيرها وسيحصل على نوع من العبثية ، والتي من المرجح أن لا يتم إقران لوحة الوسادة بها ، وسيرفض الخادم هذه الرسالة على الفور. , , , , : RSA, , . , . , .

, , RSA. , , , . , , , 1000 . e .



, . , 1000 . 1000- , 1000 1000 n, . RSA , .
4 , . , . , CRT. . . , , , , [ = a ₁ ] mod p [ = a ₂ ] mod q, q – , .



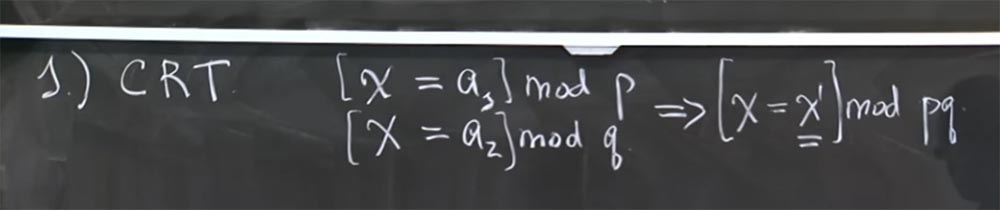
, [ = ¹ ] mod pq. ¹ , . ¹ , mod pq a ₁ a ₂ mod p q.

, ? , , n, p q.



, mod pq, mod p mod q. , , mod pq. , ? , , ?

: , ?

: , , , . , p q, n 1000 , p q 500 , . , , — , , . — . , , . 1000 512 , 2 . , 4 . [ = a ₁ ] mod p [ = a ₂ ] mod q , 4 . 2 RSA , .

, .

, Sliding windows, « ». . , .



, - , 500 , mod p mod q, d. c d? , c d . d , 500, . , , . , « ». .

c ^2x , : (c ^x ) ² :

c ^2x = (c ^x ) ²

c ^2x , 2 , cx, . , , c ^2x+1 :

c ^2x+1 = (c ^x ) ² x

.

, , , . , , , . , .

« », ? , . , , « » c ^2x+1 = (c ^x ) ² x .

, , , – , c ^2x+1 c ^2x , c. , , . , .



, :

1
3
7
...
31

. , , , .

, ^32x+y , 5 , 32- , ^y .



³² . , , , , c . «» .

29:00

دورة معهد ماساتشوستس للتكنولوجيا "أمن أنظمة الكمبيوتر". 16: « », 2


.

, . ? ? , 30% entry-level , : VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps $20 ? ( RAID1 RAID10, 24 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps , .

Dell R730xd 2 ? فقط لدينا 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV من 249 دولارًا في هولندا والولايات المتحدة! . c Dell R730xd 5-2650 v4 9000 ?