معهد ماساتشوستس للتكنولوجيا. محاضرة رقم 6.858. "أمن أنظمة الكمبيوتر." نيكولاي زيلدوفيتش ، جيمس ميكنز. 2014 سنة
أمان أنظمة الكمبيوتر هي دورة حول تطوير وتنفيذ أنظمة الكمبيوتر الآمنة. تغطي المحاضرات نماذج التهديد ، والهجمات التي تهدد الأمن ، وتقنيات الأمان بناءً على العمل العلمي الحديث. تشمل الموضوعات أمان نظام التشغيل (OS) ، والميزات ، وإدارة تدفق المعلومات ، وأمان اللغة ، وبروتوكولات الشبكة ، وأمان الأجهزة ، وأمان تطبيقات الويب.
المحاضرة 1: "مقدمة: نماذج التهديد"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 2: "السيطرة على هجمات القراصنة"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 3: "تجاوزات العازلة: المآثر والحماية"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 4: "فصل الامتيازات"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 5: "من أين تأتي أنظمة الأمن؟"
الجزء 1 /
الجزء 2المحاضرة 6: "الفرص"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 7: "وضع حماية العميل الأصلي"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 8: "نموذج أمن الشبكات"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 9: "أمان تطبيق الويب"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 10: "التنفيذ الرمزي"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 11: "لغة برمجة Ur / Web"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 12: أمن الشبكات
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 13: "بروتوكولات الشبكة"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 14: "SSL و HTTPS"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 15: "البرامج الطبية"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 16: "هجمات القناة الجانبية"
الجزء 1 /
الجزء 2 /
الجزء 3 الجمهور: كيفية تحديد x و y أولاً؟
الأستاذ: لهذا يجب أن تنظر إلى العارض في تمثيل ثنائي. لنفترض أنني أحاول حساب قيمة c
1011010 ، فقد تتكون الدرجة أيضًا من عدد أكبر من البتات. إذا أردنا إجراء إعادة تربيع ، فنحن بحاجة إلى النظر إلى أدنى بت - هنا هو 0.
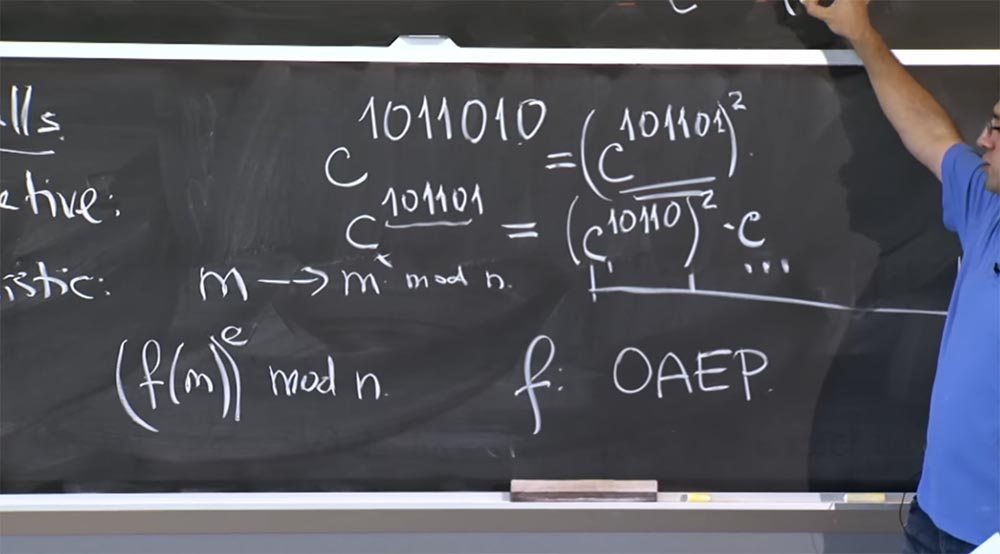
وبذلك نحصل على المساواة ج
1011010 = (ج
101101 )
2بعد ذلك ، نحتاج إلى حساب c
101101 ، وهنا لا يمكننا استخدام هذه القاعدة ، لأنها ليست 2x - ستكون x زائد 1. لذلك ، نكتب هذه المساواة:
ج
101101 = (ج
10110 )
2 ج ، لأن هذه البادئة 101101 = 10110 + 1.
لذلك ، نضرب المربع في c ، لذلك نستخدمه لإعادة التربيع.
بالنسبة لـ "النوافذ المنزلقة" ، نحتاج إلى التقاط المزيد من البتات من الطرف السفلي. إذا كنت ترغب في القيام بخدعة هنا مع "نافذة منزلقة" بدلاً من استخراج واحدة من هنا ، فعند أخذ هذا الجدول الضخم في الاعتبار ، يمكننا أخذ 3 بتات في كل مرة ، والتشبث بـ c7. إذا أخذنا أول 3 بتات من الدرجة ، نحصل على c
101101 = (c
101 )
8 c
101 .
في هذه الحالة ، لدينا بالفعل نفس مقدار الحسابات لـ (ج
101 )
8 ، ولكن يمكنك رؤية قيمة ج
101 في الجدول. والجزء في شكل (ج
101 )
8 يقول أنك ستستخدم "النوافذ المنزلقة" لحساب قيمتها.
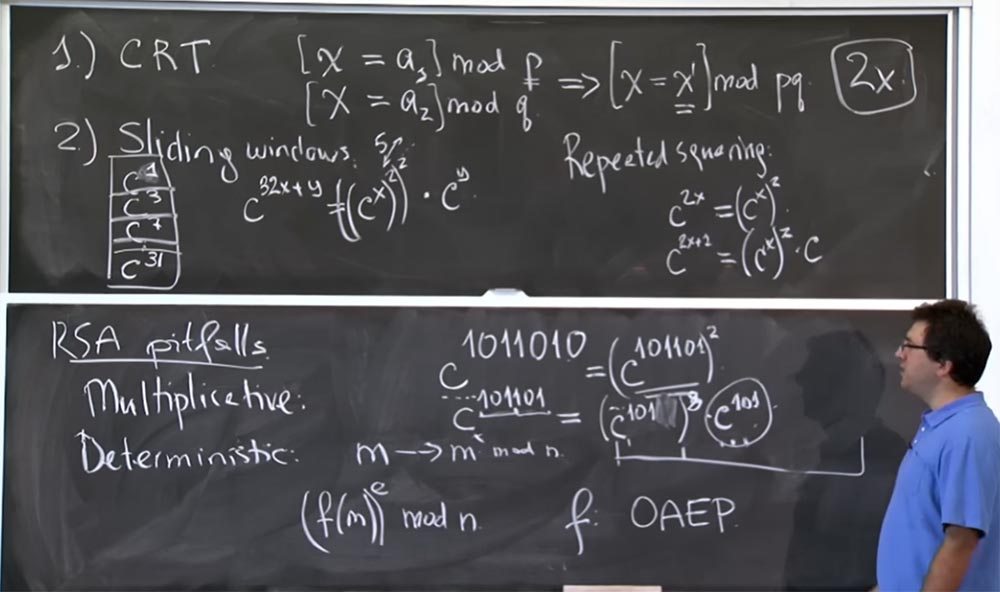
هذا يوفر الكثير من الوقت ، لأنه يجعل من الممكن استخدام القيم المضاعفة مسبقًا. قبل 10 سنوات كان يعتقد أن جدول القيم حتى 32 درجة هو الخطة المثلى من حيث الكفاءة الحسابية ، لأن هناك نوعًا من الحل الوسط هنا ، أليس كذلك؟ تقضي وقتًا في إنشاء هذا الجدول ، ولكن لا يجب أن يكون كبيرًا جدًا إذا لم تستخدم بعض السجلات كثيرًا. افترض أنك إذا قمت بإنشاء جدول قيم يصل إلى c
500 درجة ، لكنك لن تستخدم الأسس بقيمة أكبر من 128 ، ثم تضيع وقتك.
الجمهور: هل هناك أي سبب لعدم إنشاء مثل هذا الجدول العملاق مسبقًا؟ أي لحساب قيم عدد محدود من الدرجات التي يمكن التحايل عليها في الحسابات؟
البروفيسور: إذا كنت لا ترغب في إجراء العمليات الحسابية مقدما ... حسنا ، هناك شيئان. الأول هو أنه يجب أن يكون لديك رمز للتحقق مما إذا كان السجل المطلوب في الجدول ممتلئًا أم لا ، وهذا سيقلل على الأرجح من دقة التنبؤ بفروع عمليات وحدة المعالجة المركزية. في الوقت نفسه ، في الحالة العامة ، سيعمل المعالج بشكل أبطأ ، لأنه سيكون عليه التحقق مما إذا كان السجل المطلوب في الجدول. الشيء الثاني ، وهو أمر مزعج إلى حد ما ، يمكن أن يكون تسرب إدخالات الجدول من خلال القنوات الجانبية المختلفة ، أي من خلال أنماط الوصول إلى ذاكرة التخزين المؤقت. لذلك إذا كان لديك بعض العمليات الأخرى التي تعمل على نفس المعالج ، يمكنك معرفة عناوين ذاكرة التخزين المؤقت التي تمت إزالتها من ذاكرة التخزين المؤقت أو إبطائها لأن شخصًا ما لديه حق الوصول إلى السجل c
3 أو لتسجيل c
31 . وكلما زاد حجم هذا الجدول ، أصبح من الأسهل تحديد البتات الأس التي يتم استخدامها لإنشاء مفتاح RSA.
هذا الجدول العملاق قادر على معرفة عنوان ذاكرة التخزين المؤقت المفقود للمعالج ، وهذا يعني أن عملية التشفير يجب أن يكون لها حق الوصول إلى هذا الإدخال في الجدول. يخبرك هذا بدوره أن تسلسل البتات المحدد يظهر في الأس الخاص بمفتاحك الخاص. لذلك ، أفترض أنه يمكنك حسابًا رياضيًا ملء هذا الجدول بقدر ما هو مطلوب ، ولكن في الممارسة العملية لا تريد أن يتحول إلى حجم ضخم. بالإضافة إلى ذلك ، لن تتمكن من استخدام إدخالات الجدول الضخمة بشكل فعال. من المفيد جدًا استخدام سجلات جدول صغير نسبيًا بشكل متكرر ، على سبيل المثال ، لحساب c
7 ، يمكنك استخدام القيمة c
3 مرتين وهكذا.
لذا ، إليك تحسين RSA عن طريق إعادة التربيع وطرق "النافذة المنزلقة". لا أعرف ما إذا كانوا لا يزالون يستخدمون هذا الحجم من "النوافذ المنزلقة" ، ولكن على أي حال فإنه يسرع عملية الحساب ، لأنه بخلاف ذلك سيكون عليك تربيع كل جزء من الأس ثم ضربه في كل بت. لذلك ، إذا كان لديك أس 500 بت ، فسيتعين عليك إكمال 500 مربع وحوالي 256 ضربًا بواسطة c. مع "النوافذ المنزلقة" ، لا يزال عليك عمل 512 مربعًا ، لأنه لا يمكن تجنب ذلك ، ولكن عدد المضاعفات بـ c سينخفض من 256 إلى حوالي 32 بسبب استخدام الإدخالات من الجدول.
هذه هي خطة التحسين العامة ، التي تعمل على تسريع عملية الحساب بنحو مرة ونصف. هذا تحسين بسيط إلى حد ما. هناك خدعتان ذكيتان بأرقام تجعل عملية الضرب أكثر كفاءة.
الأول هو تحول مونتغمري ، في ثانية سنرى لماذا هذا مهم بشكل خاص بالنسبة لنا. يحاول هذا التحسين حل مشكلة لنا ، وهي أنه في كل مرة نقوم فيها بعملية الضرب ، نحصل على رقم يستمر في النمو والنمو بترتيب متزايد. على وجه الخصوص ، في كل من "النوافذ المنزلقة" وفي إعادة التربيع ، قمت بالفعل بضرب رقمين معًا عندما رفعت c إلى قوة y.
تكمن المشكلة في أنه إذا كانت بيانات الإدخال c
x و c
y للضرب ، على سبيل المثال ، 512 بت لكل منهما ، فسيكون حجم نتيجة الضرب 1000 بت. بعد ذلك ، تأخذ هذه النتيجة 1000 بت وتضربها مرة أخرى في شيء مثل 512 بت ، وتصبح بحجم 1500 ، 2000 ، 2500 بت وكل شيء ينمو وينمو.
ومع ذلك ، لا تريد ذلك ، لأن الضرب يزيد من ترتيب الأعداد المضروبة. وبسبب هذا ، يجب أن نحافظ على حجم رقمنا صغيرًا قدر الإمكان ، يساوي بشكل أساسي 512 بت ، لأن جميع هذه الحسابات هي mod p أو mod q.
يمكننا تقليل هذا العدد ، على سبيل المثال ، نريد حساب (((ج
س )
2 )
2 )
2 . ما يمكنك فعله هو ، على سبيل المثال ، حساب cx modulo p ، ثم تربيعه مرة أخرى modulo p ومرة أخرى تربيع modulo p. هذه الطريقة جيدة نسبيًا ، لأنها تسمح لنا بالحفاظ على حجم رقمنا في حدود 512 بت ، أي أصغر ما يمكننا الحصول عليه. هذا أمر جيد بمعنى تقليل حجم الأرقام التي نحتاج إلى مضاعفتها ، ولكن في الواقع ، فإن العملية مع هذه الوحدة p تزيد بشكل كبير من "تكلفة" الحساب.
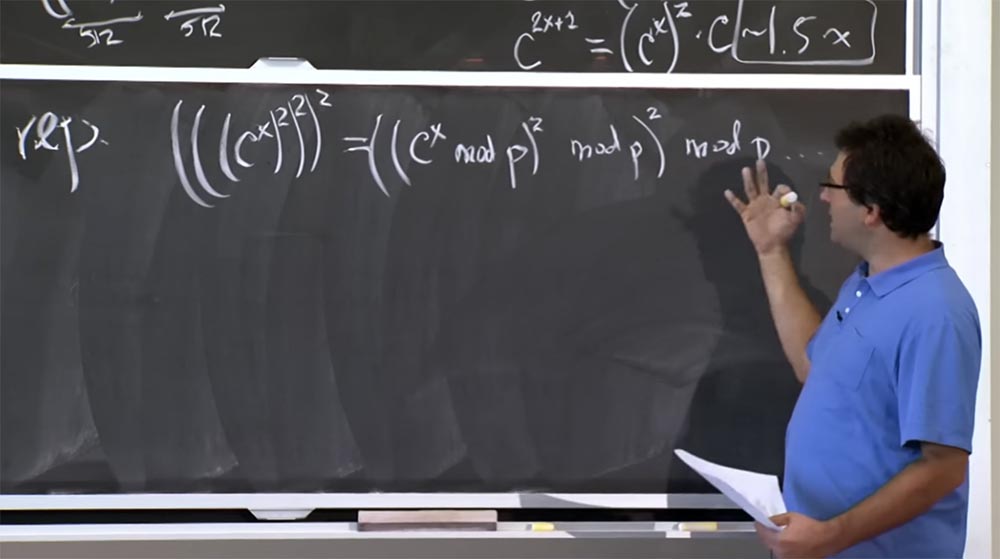
لأن الطريقة التي تحصل بها على mod p هي الانقسام. والانقسام أسوأ من الضرب. لن أسرد خوارزميات التقسيم ، لكنها بطيئة جدًا. عادة ما تحاول تجنب عمليات القسمة كلما أمكن ذلك ، لأن هذه ليست برمجة سهلة. والحقيقة هي أنك تحتاج إلى استخدام نوع من خوارزميات التقريب ، وطرق نيوتن وما شابه ، وكل هذا سيبطئ عملية الحساب.
الضرب أكثر ربحية ، ولكن استخدام عمليات التعديل أو التعديل q لتقليل حجم الأرقام سيكلف أكثر من الضرب. سأوضح لك طريقة لتجنب ذلك وكيفية إجراء حسابات سريعة باستخدام تحويل مونتغمري.
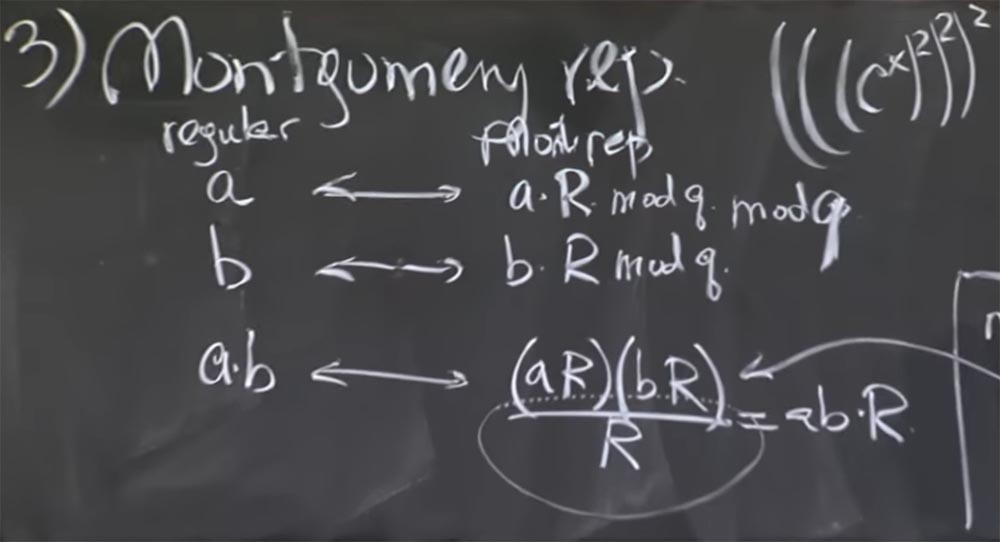
الفكرة الأساسية هي تمثيل الأعداد الصحيحة التي ستتكاثر في شكل تحويل مونتغمري. هذا في الواقع سهل للغاية. للقيام بذلك ، نقوم ببساطة بضرب رقمنا a في قيمة سحرية معينة R. بعد ثانية سأخبرك ما هو. ولكن دعنا أولاً نكتشف ما يحدث عندما نختار قيمة عشوائية لـ R.
لذا ، نأخذ رقمين ، أ و ب ، ونحولهم إلى تمثيل مونتغمري ، ونضرب كل منهم في R. ثم سيبدو منتج أ و ب في تحويل مونتغمري كما يلي:
ab <-> (aR) (bR) / R = abR
بمعنى ، تقوم بضرب aR في bR والحصول على منتج ab في مربع R. الآن لدينا اثنان روبية ، وهذا أمر مزعج قليلاً ، ولكن يمكنك تقسيمه على R. ونتيجة لذلك ، نحصل على منتج ab على R. ومن غير الواضح بعض الشيء لماذا نحتاج إلى ضرب هذا الرقم مرة أخرى. دعنا أولاً نكتشف ما إذا كان هذا صحيحًا ، ثم نفهم لماذا سيكون أسرع.
هذا صحيح بمعنى أنه سهل للغاية. إذا كنت تريد ضرب بعض الأرقام ، فأنت بحاجة إلى ضربها بقيمة R والحصول على تحويل مونتغمري. في كل مرة نضرب فيها هذين الرقمين ، يجب أن نقسمهما على R ، ثم ننظر إلى الشكل الناتج من تحويل النموذج abR. ثم ، عندما ننتهي من التربيع ، والضرب ، وكل هذه الأشياء ، سنعود إلى الشكل العادي والنتيجة للنتيجة ، ونقسمها ببساطة على R للمرة الأخيرة.
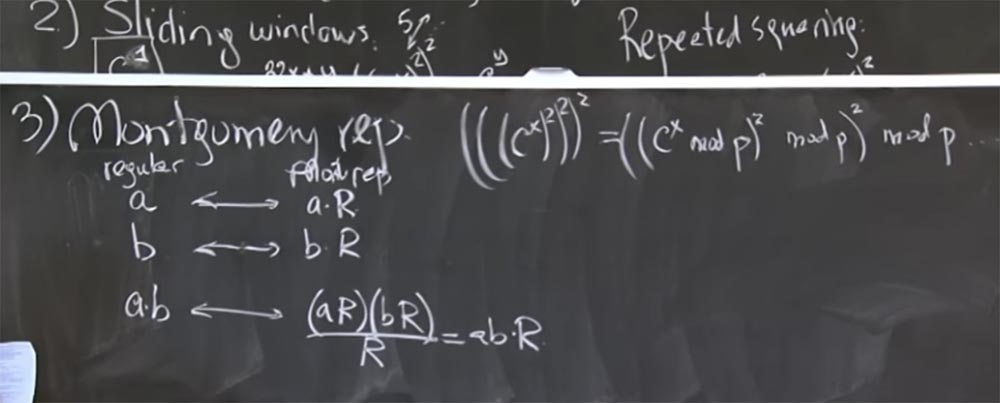
الآن فكر في كيفية اختيار الرقم الأنسب لـ R لجعل القسمة على R عملية سريعة جدًا. وأروع شيء هنا هو أنه إذا كان القسمة على R سريعًا جدًا عندما يكون عددًا صغيرًا ، وليس علينا القيام بهذا التعديل q كثيرًا. على وجه الخصوص ، aR ، دعنا نقول ، سيكون لها أيضًا حجم حوالي 500 بت ، لأن كل هذا هو في الواقع mod p أو mod q. وبالتالي ، فإن aR هو 500 بت ، سيكون bR أيضًا 500 بت ، بحيث يكون المنتج (aR) (bR) 1000 بت. R سيكون أيضًا رقمًا مناسبًا من 500 بت ، بحجم ص. وإذا تمكنا من جعل عملية القسمة سريعة بما فيه الكفاية ، فستكون نتيجة ab أيضًا رقم 500 بت تقريبًا ، حتى نتمكن من الضرب دون الحاجة إلى قسم إضافي. القسمة على R أكثر ربحية وتعطينا نتيجة صغيرة ، والتي تتجنب استخدام mod p في معظم المواقف.
إذن ما هو رقم R الغريب الذي أتحدث عنه طوال الوقت؟ لها قيمة من 2 إلى 512 درجة:
R =
2512سيكون 1 ومجموعة من الأصفار ، لذلك من السهل أن تضرب في هذا العدد ، لأنه يكفي فقط إضافة مجموعة من الأصفار إلى النتيجة. يمكن أن يكون التقسيم بسيطًا أيضًا إذا كانت البتات الأقل أهمية للنتيجة صفرًا. لذلك إذا كانت لديك قيمة من كومة من البتات مصحوبة بـ 512 أصفار ، فإن القسمة على 2 إلى 512 درجة ستكون بسيطة جدًا - فأنت فقط تسقط الأصفار على الجانب الأيمن ، وهذه عملية قسمة صحيحة تمامًا.
المشكلة الصغيرة هي أنه ليس لدينا أصفار على الجانب الأيمن عند إجراء هذا الضرب. لدينا أرقام 512 بت حقيقية باستخدام جميع 512 بت.
إن منتج (aR) بواسطة (bR) هو أيضًا عدد حقيقي من ترتيب 1000 بت ، لذلك لا يمكننا فقط إسقاط البتات الأقل أهمية. لكن النهج المعقول يعتمد على حقيقة أن الشيء الوحيد الذي يقلقنا هو قيمة mod p. وبالتالي ، يمكنك دائمًا إضافة p متعددة إلى هذه القيمة دون تغيير مكافئها p. ونتيجة لذلك ، يمكننا إضافة مضاعفات قيم p بحيث تصبح كل البتات الأقل أهمية أصفارًا. دعونا نلقي نظرة على بعض الأمثلة البسيطة. لن أكتب 512 بت على السبورة ، لكني سأعطي مثالاً قصيراً فقط.
لنفترض أنه في حالتنا R = 2
4 = 10000. هذا حجم أصغر بكثير مما هو عليه في الواقع. دعونا نرى كيف يعمل تحويل مونتغمري. نحاول حساب mod q ، حيث q = 7. في الصيغة الثنائية q = 7 تساوي (111).
افترض أيضًا أننا قمنا ببعض الضرب (aR) (bR) ، وفي التمثيل الثنائي تكون النتيجة 11010 ، أي أن هذه ستكون قيمة المنتج (aR) (bR). كيف نقسمها على R؟
من الواضح ، ليست كل البتات الأربعة الأقل أهمية هي أصفار ، لذلك لا يمكننا فصلها فقط ، ولكن يمكننا إضافة كميات مضاعفات q. على وجه الخصوص ، يمكننا إضافة 2 مرات في q ، مع 2q = 1110 في التمثيل الثنائي. نتيجة للإضافة ، نحصل على 101000 ، آمل أن أفعل كل شيء بشكل صحيح.
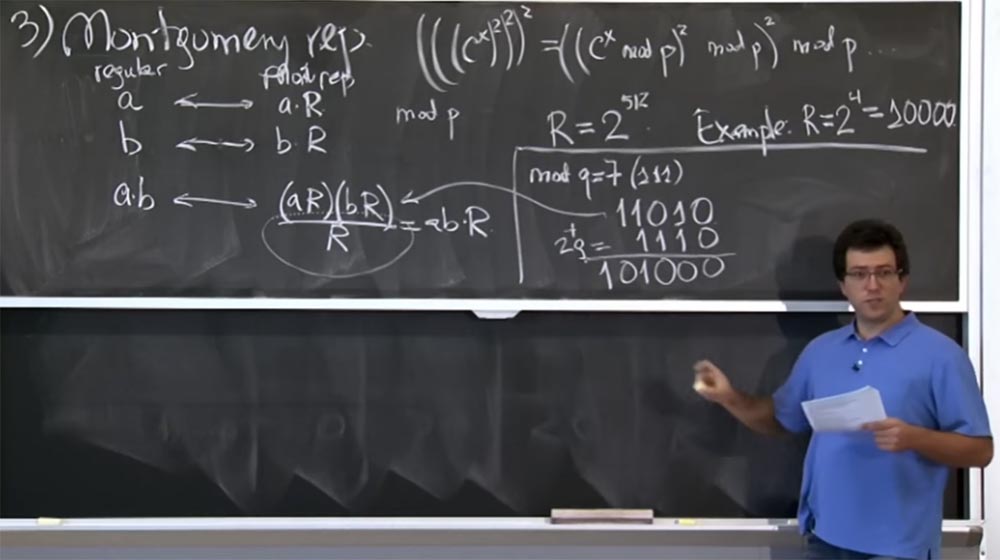
لذا حصلنا على المجموع (أ ر) (ب ر) + 2 ف. في الواقع ، نحن لا نهتم ب + 2q ، لأن كل ما يهمنا هو قيمة mod q. الآن نحن قريبون من الهدف ، لأن لدينا ثلاثة أصفار على اليمين. الآن يمكننا إضافة المزيد من q. دعنا نقول هذه المرة سيكون 8q ، والذي سيكون 111000. مرة أخرى ، أضف خطوطنا واحصل على 1100000. الآن لدينا الأصلي (aR) (bR) + 2q + 8q = 1100000. وأخيرًا ، يمكننا بسهولة تقسيم هذا الشيء إلى R ، يسقط فقط أربعة أصفار منخفضة.
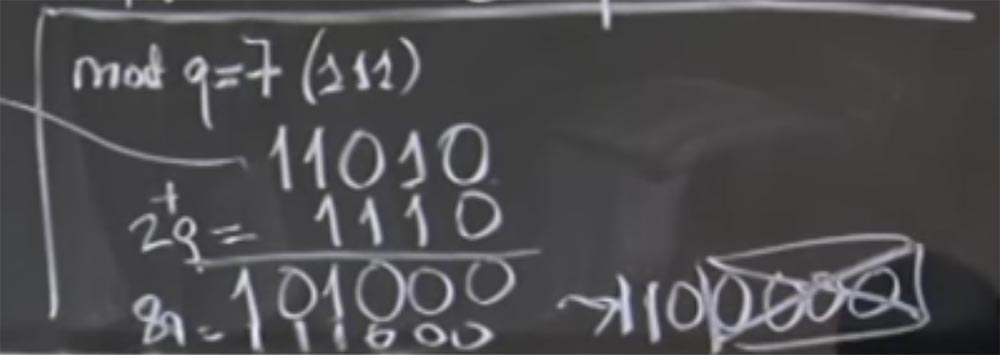الجمهور: المنتج (aR) (bR) سينتهي دائمًا بـ 1024 أصفار؟
البروفيسور: لا ، وسأشرح ما يمكن أن يكون الارتباك. لنفترض أن الرقم a هو 512 بت ، قمنا بضربه في R وحصلنا على رقم 1000 بت. في هذه الحالة ، أنت على حق ، aR هو الرقم الذي تكون فيه البتات العالية a ، والبتات المنخفضة كلها أصفار. ولكن بعد ذلك نقوم بتنفيذ mod q لتصغيره. لذلك ، حجم 1024 بت بشكل عام هو مصادفة ، حيث أن هذا الرقم يحتوي على هذه الأصفار المنخفضة فقط أثناء التحويل الأول ، ولكن بعد القيام ببعض المضاعفات ، ستكون بتات عشوائية.
من أجل عدم تضليلك ، كان علي أن أكتب mod q هنا بعد aR وبعد bR - هنا أقوم بإضافته - وحساب هذا mod q بمجرد إجراء التحويل لتقليل القيمة.
التحويل الأولي شاق إلى حد ما ، أو على الأقل مكلف مثل التعديل التقليدي في الضرب. الشيء الرائع هو أنك تدفع هذا السعر مرة واحدة عند إجراء تحويل مونتغمري ، وبعد ذلك ، بدلاً من تحويله مرة أخرى في كل خطوة من الحسابات ، يمكنك الاحتفاظ به في شكل عرض مونتغمري.
تذكر أنه للارتقاء إلى قوة تحتوي على 512 بت ، سيتعين عليك القيام بأكثر من 500 مضاعف ، لأننا يجب أن نقوم بما لا يقل عن 500 مربع وغيرها. لذا تقوم بتعديل q مرتين ثم تحصل على الكثير من عمليات التقسيم البسيطة إذا بقيت في هذا الشكل من تمثيل الأرقام. وفي النهاية ، تقوم بعمل القسمة على R للعودة إلى هذا النموذج ab.
لذا ، بدلاً من إجراء mod q 500 مرة لكل خطوة من عملية الضرب ، فإنك تقوم بتعديل q مرتين ثم تستمر في إجراء هذه الأقسام بواسطة R بأقل تكلفة.
الجمهور: عند إضافة مضاعفات q ثم القسمة على R ، هل لدينا الباقي؟
الأستاذ: في الواقع mod q يعني الباقي عندما تقسمه على q. ببساطة ، x + yq mod q = x. في هذه الحالة ، هناك خاصية مفيدة أخرى - أن جميع الوحدات هي بدائل. هذا صحيح مثل حقيقة أنه إذا كان لديك (x + yq / R) mod q ، فإنه يساوي x / R mod q.
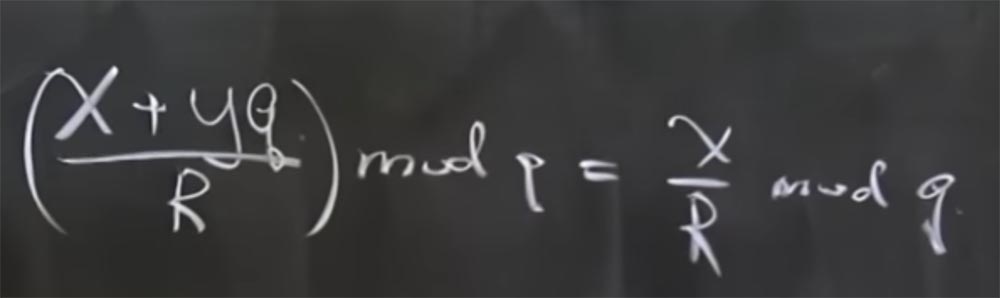
سبب التفكير هو أنه لا توجد عمليات تقسيم حقيقية في الحساب المعياري ، إنه مجرد انعكاس. في الواقع ، هذا يعني أنه إذا كان لدينا (x + yq) مضروبًا في R المقلوب المحسوب بواسطة mod q ، فإنه يساوي مجموع منتجين: المنتج x من R المقلوب بواسطة mod q والمنتج yq بالمقلوب R بواسطة mod q. علاوة على ذلك ، تم تقليل الحد الأخير ، لأنه شيء مضروب في q.
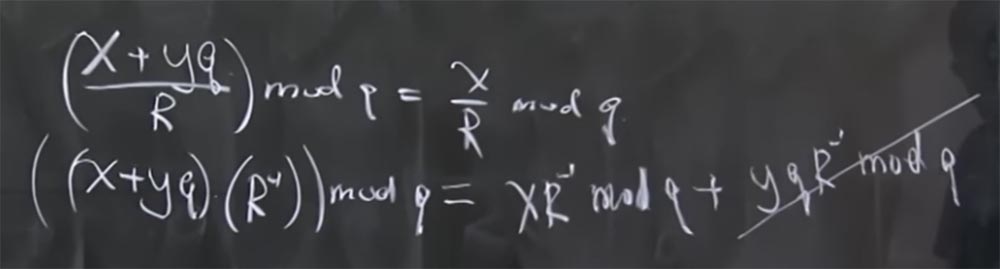
بالنسبة لأشياء مثل جمع 2q و 8 q وما إلى ذلك ، هناك صيغة تسرع عملية الحساب. لقد قمت بذلك تدريجيًا ، وحُسبت أولاً 2q ، ثم 8q وما إلى ذلك ، لكن مواد المحاضرة لها صيغة كاملة يمكن استخدامها ، أنا فقط لا أريد أن أضيع الوقت في كتابتها على السبورة. يسمح لك بحساب ما يجب أن يضيفه مضاعف قيمة q بحيث تتحول كل البتات الأقل أهمية إلى 0. ثم يتبين أنه من أجل إجراء القسمة على R ، تحتاج فقط إلى حساب هذا السحر السحري من q ، وإضافته ، ثم تجاهل القيمة المنخفضة صفر بت ، وهذا سيعيد رقمك إلى 512 بت بغض النظر عن حجم النتيجة التي تحصل عليها.
ولكن هناك دقة واحدة. السبب الوحيد الذي يجعلنا نتحدث عن هذا هو أن هناك شيئًا مضحكًا يحدث هنا ، مما يسمح لنا بمعرفة معلومات حول التوقيتات. على وجه الخصوص ، على الرغم من قسمة R ، فإننا ما زلنا نعلم أن النتيجة ستكون حوالي 512 بت. ولكن يمكن أن يكون أكبر من q ، لأن q ليس رقم 512 بت ، ويمكن أن يكون أقل بقليل من R.
لذلك قد يكون من الضروري بعد طرح هذا القسمة المفيدة من R أن نطرح q مرة أخرى ، لأننا نحصل على شيء صغير ، ولكن لا يزال غير صغير بما فيه الكفاية. لذلك هناك احتمال أنه بعد هذا التقسيم قد نضطر إلى طرح q مرة أخرى. ويمكن استخدام هذا الطرح كجزء من الهجوم ، لأن عملية الطرح تضيف وقت الحساب.
واكتشف شخص ما - ليس هؤلاء الأشخاص ، ولكن شخصًا في العمل السابق - أن هناك فرصة للقيام بشيء يسمى التخفيض الإضافي ، أو التخفيض الإضافي. , . , xd mod q, - x mod q, 2R. .
, x mod q , . , cd.
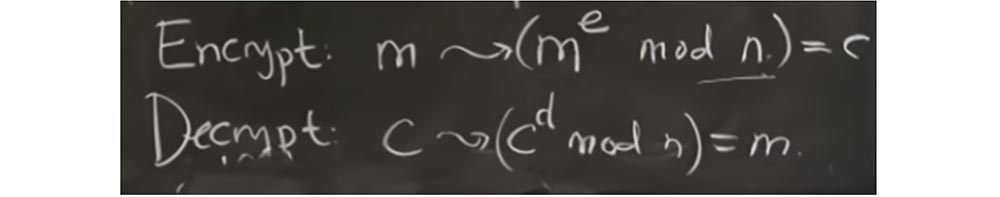
, extra reduction , X , , , q.
, c, extra reduction , c — q. , , q . , extra reduction, , , X mod q , = q + έ, . , . , , , , extra reduction .
: , ?
: , extra reduction? , , , . , . , , extra reduction, , , . , . , , mod q. , , , . , mod q , , .
, . , - , . — , . , - , extra reduction .
, . , OpenSSL, , . , mod q . , , .
, , , , a b. — 512- . , 32- , , 64- ? ?
- ? , , a b .
, , 512 , 64- , 32- . a : a
1 a
0 , a
0 , a
1 — . b – b
1 b
0 .
ab 3- : a
1 b
1 , a
0 b
0 , a
1 b
0 + a
0 b
1 . .
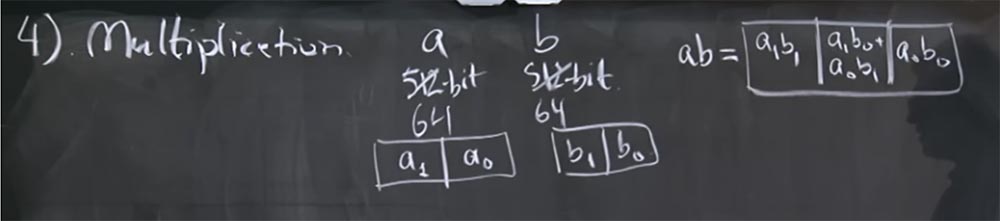
55:00
دورة معهد ماساتشوستس للتكنولوجيا "أمن أنظمة الكمبيوتر". 16: « », 3.
, . ? ? ,
30% entry-level , : VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps $20 ? ( RAID1 RAID10, 24 40GB DDR4).
VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps ,
.
Dell R730xd 2 ? فقط لدينا
2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV من 249 دولارًا في هولندا والولايات المتحدة! . c Dell R730xd 5-2650 v4 9000 ?