معهد ماساتشوستس للتكنولوجيا. محاضرة رقم 6.858. "أمن أنظمة الكمبيوتر." نيكولاي زيلدوفيتش ، جيمس ميكنز. 2014 سنة
أمان أنظمة الكمبيوتر هي دورة حول تطوير وتنفيذ أنظمة الكمبيوتر الآمنة. تغطي المحاضرات نماذج التهديد ، والهجمات التي تهدد الأمن ، وتقنيات الأمان بناءً على العمل العلمي الحديث. تشمل الموضوعات أمان نظام التشغيل (OS) ، والميزات ، وإدارة تدفق المعلومات ، وأمان اللغة ، وبروتوكولات الشبكة ، وأمان الأجهزة ، وأمان تطبيقات الويب.
المحاضرة 1: "مقدمة: نماذج التهديد"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 2: "السيطرة على هجمات القراصنة"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 3: "تجاوزات العازلة: المآثر والحماية"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 4: "فصل الامتيازات"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 5: "من أين تأتي أنظمة الأمن؟"
الجزء 1 /
الجزء 2المحاضرة 6: "الفرص"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 7: "وضع حماية العميل الأصلي"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 8: "نموذج أمن الشبكات"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 9: "أمان تطبيق الويب"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 10: "التنفيذ الرمزي"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 11: "لغة برمجة Ur / Web"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 12: أمن الشبكات
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 13: "بروتوكولات الشبكة"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 14: "SSL و HTTPS"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 15: "البرامج الطبية"
الجزء 1 /
الجزء 2 /
الجزء 3المحاضرة 16: "هجمات القناة الجانبية"
الجزء 1 /
الجزء 2 /
الجزء 3 الجمهور: هل تستخدم طريقة كاراتسوبا؟
البروفيسور: نعم ، هذه طريقة ضرب ذكية لا تتطلب أربع مراحل من الحساب. يتم تدريس طريقة كاراتسوبا في دورة .601 ، أو كيف يتم تحديدها اليوم؟
الجمهور: 042.
الأستاذ: 042 ممتاز. نعم ، هذه طريقة جيدة للغاية. تقريبا كل مكتبة التشفير تستخدمه. لأولئك منكم الذين ليسوا خريجين من معهدنا - أقول هذا لأن لدينا طلاب دراسات عليا هنا - سأكتب عن طريقة كاراتسوبا على السبورة. هنا تحتاج إلى حساب ثلاث قيم:
أ
1 ب
1(أ
1 - أ
0 ) (ب
1 - ب
0 )
أ
0 ب
0وبالتالي ، تقوم بإجراء 3 ضربات بدلاً من أربعة ، وتبين أنه يمكنك استعادة هذه القيمة
1 b
0 + a
0 b
1 من نتائج الضرب الثلاثة هذه.
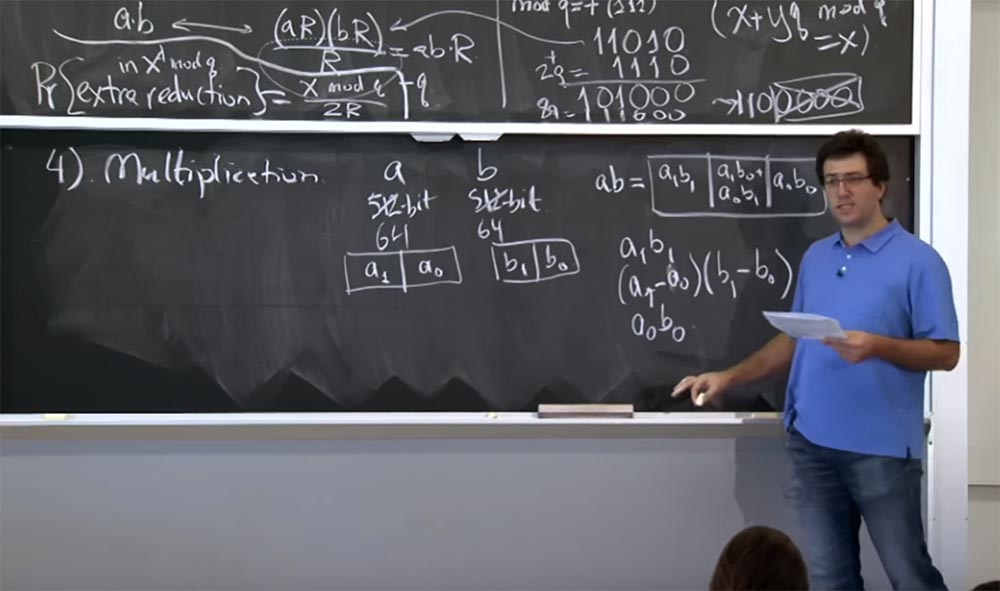
الطريقة الخاصة للقيام بذلك هي ... دعني أضعه في شكل مختلف.
لذا سيكون لدينا:
(2
64 + 2
32 ) (أ
1 ب
1 ) +
(2
32 ) (- (أ
1 - أ
0 ) (ب
1 - ب
0 )
(2
32 + 1) (أ
0 ب
0 )
هذا ليس واضحًا جدًا ، ولكن إذا قمت بتفصيل التفاصيل ، فقم في النهاية بإقناع نفسك بأن هذه القيمة في هذه الأسطر الثلاثة تعادل ab ، ولكن في نفس الوقت تقلل من الحساب بضرب واحد. والطريقة التي نطبق بها هذا على المضاعفات الأكثر ضخامة هي أنك تستمر في الانخفاض بشكل متكرر. لذا ، إذا كان لديك قيم 512 بت ، يمكنك تقسيمها إلى مضاعفة 256 بت. تقوم بثلاث مضاعفات 256 بت ، كل مرة بشكل متكرر باستخدام طريقة كاراتسوبا. في النهاية ، تنخفض حساباتك إلى حجم الماكينة ويمكن معالجتها من خلال تعليمات آلة واحدة.
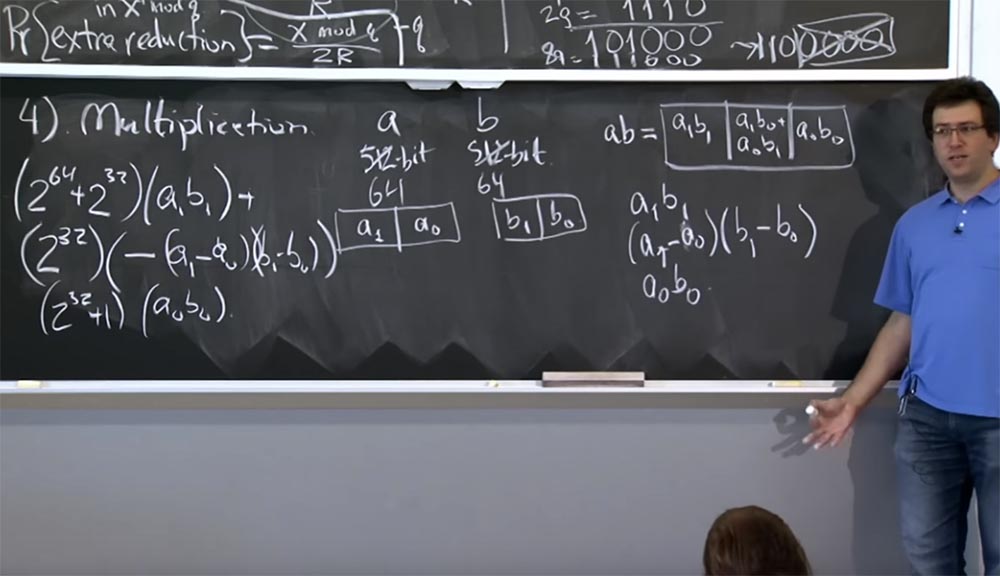
فأين هجوم التوقيت؟ كيف يستخدم هؤلاء الرجال الضرب Karatsuba؟ تبين أن OpenSSL قلق من نوعين من الضرب قد يتعين عليك القيام به.
الأول هو ضرب رقمين كبيرين من نفس الحجم تقريبًا. يحدث هذا عدة مرات عندما نقوم بإجراء أسي معياري ، لأن جميع القيم التي سنضاعفها سيكون حجمها حوالي 512 بت. لذلك ، عندما نضرب c في y أو مربع ، فإننا نضرب شيئين من نفس الحجم تقريبًا. في هذه الحالة ، تكون طريقة Karatsuba منطقية للغاية ، لأنها تقلل من حجم الأرقام المربعة بنحو 1.58 مرة ، مما يسرع بشكل كبير من عملية الحساب.
النوع الثاني من الضرب هو عندما يقوم OpenSSL بضرب رقمين يختلف حجمهما بشكل كبير عن بعضهما: أحدهما كبير جدًا والآخر صغير جدًا. في هذه الحالة ، يمكنك أيضًا استخدام طريقة Karatsuba ، لكنها ستعمل بشكل أبطأ من الضرب البدائي. افترض أنك تضرب رقم 512 بت في رقم 64 بت ، سيتعين عليك رفع كل بت من الرقم الأول إلى قوة 64 ، مما يؤدي إلى تباطؤ عملية 2n بدلاً من تسريع n / 1.58. لذلك ، حاول هؤلاء الأشخاص الذين يستخدمون OpenSSL القيام بذكاء أكبر ، وهنا بدأت المشاكل.
قرروا أنهم سوف يتحولون ديناميكيًا بين طريقة كاراتسوبا الفعالة وأسلوب الضرب في المدارس الابتدائية. كانت ارشاداتهم على النحو التالي. إذا كان الرقمان اللذان تقومان بضربهما يتألفان من نفس عدد الكلمات الآلية ، أو على الأقل لديهم نفس عدد البتات مثل وحدات 32 بت ، فسيتم استخدام طريقة Karatsuba. إذا كان هناك رقمان يختلفان اختلافًا كبيرًا في الحجم عن بعضهما البعض ، يتم إجراء التربيع أو الضرب البسيط المباشر.
في هذه الحالة ، يمكنك تتبع كيفية حدوث التحول إلى طريقة أخرى للضرب. نظرًا لأن لحظة التبديل لا تمر بدون أي أثر ، بعد ذلك سيكون من الملاحظ ما إذا كانت تتطلب الآن وقتًا أطول كثيرًا للضرب أو أقل بكثير من ذي قبل. استغل الباحثون هذا الظرف لتنظيم هجوم باستخدام طريقة التوقيت.
أعتقد أنني انتهيت من إخبارك بكل الحيل الغريبة التي يستخدمها الناس عند تنفيذ RSA في الممارسة. الآن دعنا نحاول جمعها معًا واستخدامها فيما يتعلق بخادم الويب بالكامل لمعرفة كيف يمكنك "قطع" القطع التي تهمنا من حزمة شبكة الإدخال.
إذا كنت تتذكر من المحاضرة على HTTPS ، فإن خادم الويب يحتوي على مفتاح سري. يستخدم هذا المفتاح السري لإثبات أنه المالك الصحيح لجميع الشهادات عبر HTTPS أو TLS. ويرجع ذلك إلى حقيقة أن العملاء يرسلون بعض البتات المختارة عشوائيًا ، ويتم تشفير هذه البتات باستخدام المفتاح العام للخادم ، ويقوم الخادم بفك تشفير هذه الرسالة باستخدام بروتوكول TLS. وإذا تم فحص الرسالة ، يتم استخدام هذه البتات العشوائية لإنشاء جلسة اتصال.
ولكن في حالتنا ، لن يتم التحقق من هذه الرسالة ، لأنه سيتم إنشاؤها بطريقة خاصة ، وعندما يتبين أن البتات الإضافية لا تتطابق ، فسيرجع الخادم خطأ بمجرد انتهاء فك تشفير رسالتنا.
هذا ما سنفعله هنا. سيتلقى الخادم - يمكنك افتراض أنه Apache مع SSL مفتوح - رسالة من العميل يعتبرها نصًا مشفرًا أو نصًا مشفرًا افتراضيًا أنشأه العميل. أول شيء نقوم به مع النص المشفر c هو فك تشفيره باستخدام الصيغة مع → (c
d mod n) = m.
إذا كنت تتذكر التحسين الأول ، فسنطبق نظرية الصينية المتبقية ونقسم نصنا إلى جزأين: أحدهما لحساب mod p ، والآخر بواسطة mod q ، ثم دمج النتائج. أولاً ، خذ c وتمثيلها بكميتين: الأولى تسمى c
0 ، وسوف تساوي mod q ، والثانية c
1 ، وستكون مساوية لـ c mod p. ثم سنفعل نفس الشيء لحساب c لـ d mod p و c لـ d mod q.
بعد ذلك ، سننتقل إلى عرض مونتغمري لأن هذا سيجعل مضاعفاتنا سريعة جدًا. لذا فإن الشيء التالي الذي ستقوم به SSL برقمك هو حساب c
0 '، والذي سيكون مساوياً لـ c
0 R mod q والقيام بالشيء نفسه أدناه للقيمة c1 ، لن أكتب هذا لأنه يبدو نفس الشيء .
الآن بعد أن انتقلنا إلى نموذج مونتغمري ، يمكننا في النهاية إجراء مضاعفاتنا ، وهنا سنستخدم تقنية "النافذة المنزلقة". بمجرد أن نحصل على c
0 '، نجعل هذا رفع بسيط c
0 ' إلى قوة d في mod q. وهنا ، نظرًا لأننا نحسب هذه القيمة لـ d ، فسنستخدم "النوافذ المنزلقة" لبتات الأس d ، وسنستخدم أيضًا طريقة Karatsuba أو الضرب المعتاد ، اعتمادًا على حجم المعاملات لدينا.
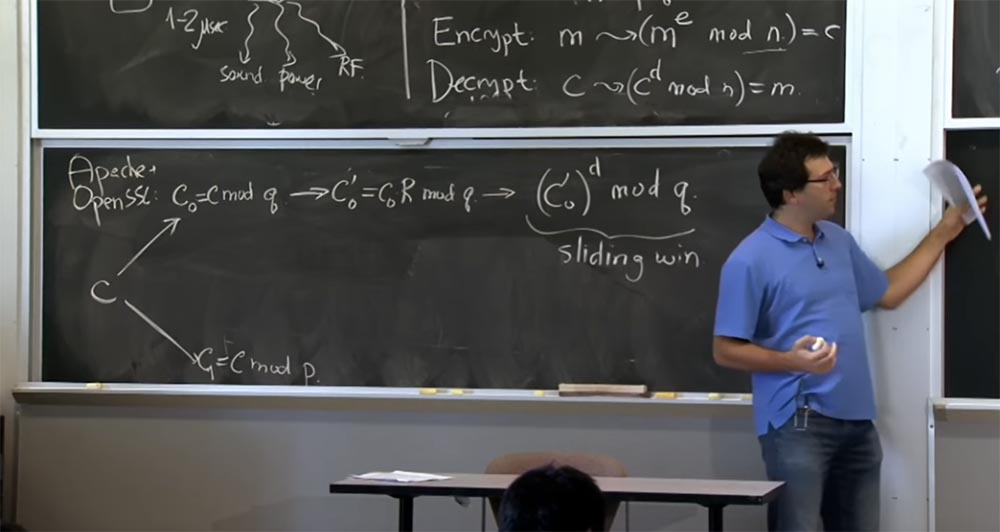
لذا ، إذا اتضح أن هذه القيمة c
0 'ونتائج التربيع التي تم الحصول عليها مسبقًا هي نفس الحجم ، فإننا نستخدم طريقة Karatsuba. إذا كان c
0 'صغيرًا جدًا ، وكانت النتيجة السابقة للضرب كبيرة ، فسوف نربّع ونضرب بالطريقة المعتادة. هنا نستخدم "النوافذ المنزلقة" وطريقة Karatsuba بدلاً من الضرب العادي.
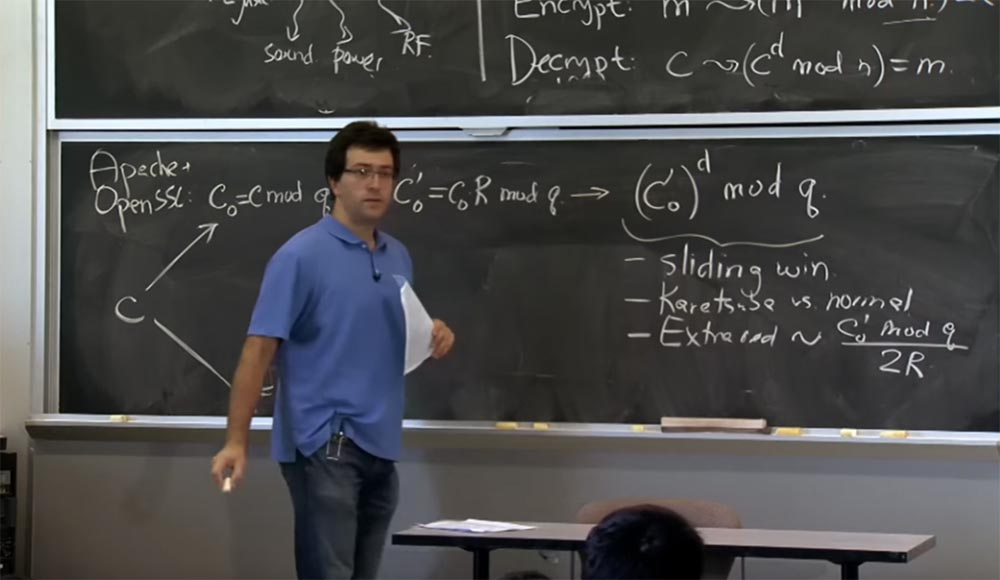
أيضا في هذه المرحلة ، تظهر تخفيضات إضافية. لأنه مع كل عملية ضرب ، ستكون التخفيضات الإضافية متناسبة مع ما نرفعه إلى قوة مع mod q ، أي بالقيمة (c
0 ')
د . هنا ، مع اتصال بسيط بالصيغة ، سيكون احتمال التخفيضات الإضافية متناسبًا مع القيمة c
0 'mod q مقسومة على 2R. في هذا المكان يظهر القليل الذي يؤثر على التوقيت.
في الواقع ، هناك تأثيران محتملان: استخدام طريقة Karatsuba بدلاً من الضرب العادي وظهور اختصارات إضافية ستقوم بها.
في ثانية سترى كيف يمكن استخدامه. الآن ، عندما تحصل على هذه النتيجة لـ mod q وستحصل على نتيجة مماثلة لـ mod p ، يمكنك في النهاية إعادة تجميع هذين الجزأين في الأعلى والأسفل واستخدام CRT ، وهي نظرية الباقي الصينية.
وما تحصل عليه من CRT نتيجة لذلك ... آسف ، أعتقد أننا بحاجة إلى تحويل هذا مرة أخرى من نموذج مونتغمري أولاً. لذلك ، قبل إعادة التركيب ، نقوم بتحويل الجزء العلوي إلى التعبير (c
0 ')
d / R mod q وإرجاع قيمنا cd mod q. في الجزء السفلي ، نحصل على ص.
يمكنك الآن استخدام CRT للحصول على قيمة c
d mod n. آسف على الخط الصغير ، لم يكن لدي ما يكفي من السبورة. حول نفس الشيء الذي نحصل عليه هنا أدناه لـ
1 ، ويمكننا أخيرًا الحصول على النتيجة ، أي الرسالة m.
وبالتالي ، يأخذ الخادم حزمة واردة يستقبلها ، ويقوم بتشغيلها من خلال خط الأنابيب بأكمله ، وينفذ جزأين من خط الأنابيب هذا ، وينتهي برسالة غير مشفرة m تساوي cd mod m. ثم سيتحقق من حشوة الحشو لهذا المنصب. في حالة هجومنا المحدد ، أنشأنا بطريقة لا تتطابق فيها هذه الإضافة في الواقع. لقد اخترنا القيمة c للاستدلال الذي لا يقوم بتشفير الرسالة الحقيقية مع إضافة المساحة الصحيحة.
وبالتالي ، لا تجتاز الإضافة الاختبار ، سيحتاج الخادم إلى تسجيل خطأ ، وإرسال رسالة خطأ إلى العميل وقطع الاتصال. لذا ، سنقيس الوقت الذي يستغرقه الخادم لتمرير رسالتنا عبر خط الأنابيب هذا. هل لديك أي أسئلة حول عملية معالجة رسالة من قبل الخادم وجمع كل هذه التحسينات؟
الجمهور: في رأيي ، هناك خطأ في مؤشر الحجم ج.
الأستاذ: نعم ، أنت على حق ، فأنا أضيف الفهرس 0 ، وهنا يجب أن يكون c
0 d mod q.
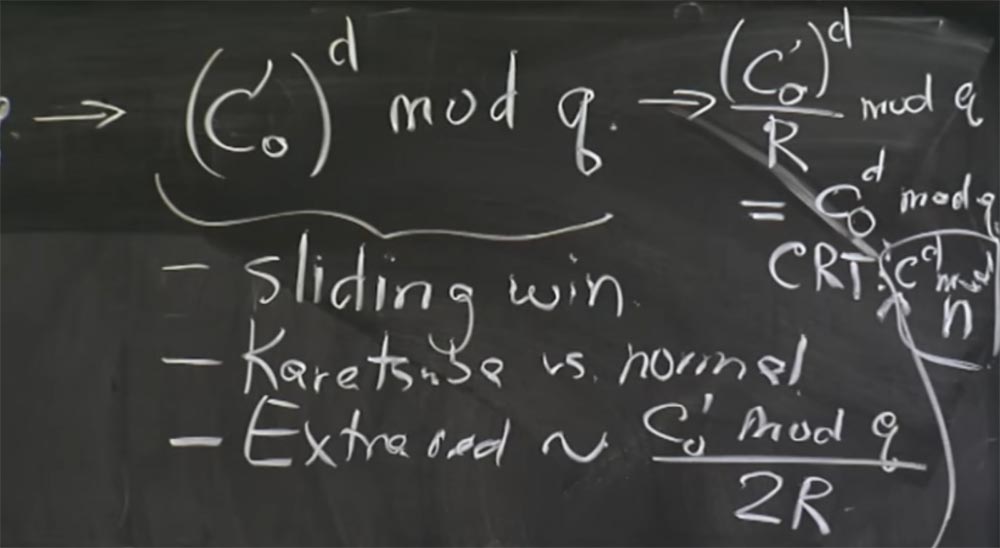الجمهور: عند القسمة على R mod q ، ألا توجد افتراضات حول مقدار q الذي يجب إضافته لزيادة تقليل البتات المنخفضة إلى أصفار؟
أستاذ: نعم ، أنت على حق ، في هذه المرحلة الأخيرة (c
0 ')
d / R mod q قد يكون هناك تخفيضات إضافية. لذا يجب أن نقوم بهذا القسمة على R بالطريقة الصحيحة ، وربما يجب أن نفعل نفس الشيء مثل إجراء تخفيض Montgomery هنا ، عندما نقسمه على R ، لتحويل القيمة مرة أخرى. نظرًا لأنه في بداية الحسابات ، ليس من الواضح بالضبط مقدار q الذي يجب أن نضيفه ، فنحن نستخدم طريقة التحديد ، ونتلف الأصفار المنخفضة ، ثم نجعل mod q مرة أخرى ، وربما تخفيضًا إضافيًا. أنت محق تمامًا ، في هذه الحالة ، يكون نفس القسمة بالضبط بواسطة R mod q لكل خطوة من خطوات الضرب في مونتغمري.
فكيف تستفيد من هذا؟ كيف يمكن للمهاجم حل المفتاح السري للخادم بقياس الوقت الذي يستغرقه إكمال العمليات؟ هؤلاء الرجال لديهم خطة تقوم على تخمين بت مفتاح خاص واحد في كل مرة. يمكننا أن نفترض أن المفتاح السري هو الأس المشفر d ، لأنك تعرف e وتعرف n ، هذا هو المفتاح العام. الشيء الوحيد الذي لا تعرفه هو د.
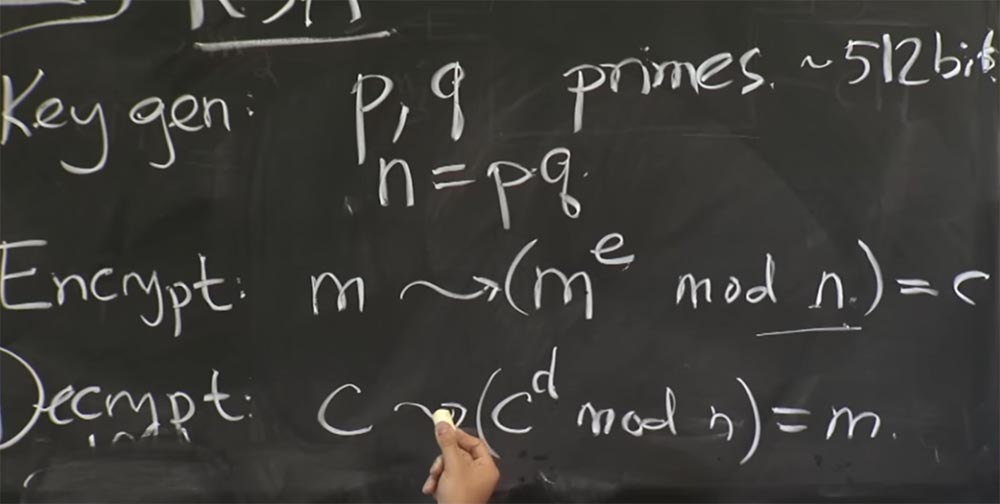
في الواقع ، في هذا الهجوم ، لا يخمنون مباشرة قيمة د ، لأنها معقدة إلى حد ما. بدلاً من ذلك ، يعتبرون q أو p ، بغض النظر عن أي من هاتين الكميتين. بمجرد تخمين ما يهم p أو q ، يمكنك حساب n = pq. بعد ذلك ، إذا كنت تعرف قيم p و q ، يمكنك حساب الوظيفة φ التي تحدثنا عنها سابقًا. سيسمح لك ذلك بالحصول على قيمة d من قيمة e. وبالتالي ، فإن هذا العامل لقيمة n مهم للغاية ؛ يجب أن يبقى سريًا من أجل ضمان أمن RSA.
لذا ، في الواقع ، كان هؤلاء الرجال ينوون تخمين قيمة q من خلال تحليل توقيتات خط الأنابيب هذا. ماذا يفعلون لهذا؟ إنهم يختارون بعناية القيمة الأولية لقيمة c ويقيسون وقت مرورها عبر خط أنابيب الخادم.
على وجه الخصوص ، هناك جزءان لهذا الهجوم ، ويجب عليك اتخاذ بعض الخطوات الأولية لتخمين البتات القليلة الأولى. بعد ذلك ، بمجرد أن تحصل على البتات القليلة الأولى ، يمكنك تخمين الجزء التالي. لذلك ، دعني لا أخبرك بالتفصيل كيف يخمنون أول بتين ، لأنه في الواقع من المثير للاهتمام أن نفكر في كيفية تخمينهم في الجزء التالي. إذا كان لدينا الوقت ، فسوف نعود إلى كيفية وصف التخمين لعدة بتات أولية في مقالة محاضرة.
لذا ، افترض أن لديك افتراض g حول البتات في قيمة هذا q. دع هذه القيمة تتكون من مثل هذه البتات: g = g
0 g
1 g
2 ... وهكذا. بدلاً من ذلك ، إنها ليست حتى g ، ولكن الأجزاء الحقيقية من q ، لذا دعني أعيد كتابتها على النحو التالي: g = q
0 q
1 q
2 .... نعتقد أن هذه q بتات عالية ، ونحاول تخمين البتات أقل وأقل. افترض أننا نعرف قيمة q حتى البت qj ، ثم تتبعها جميع الأصفار. ليس لديك فكرة عن ما تبقى من البتات.
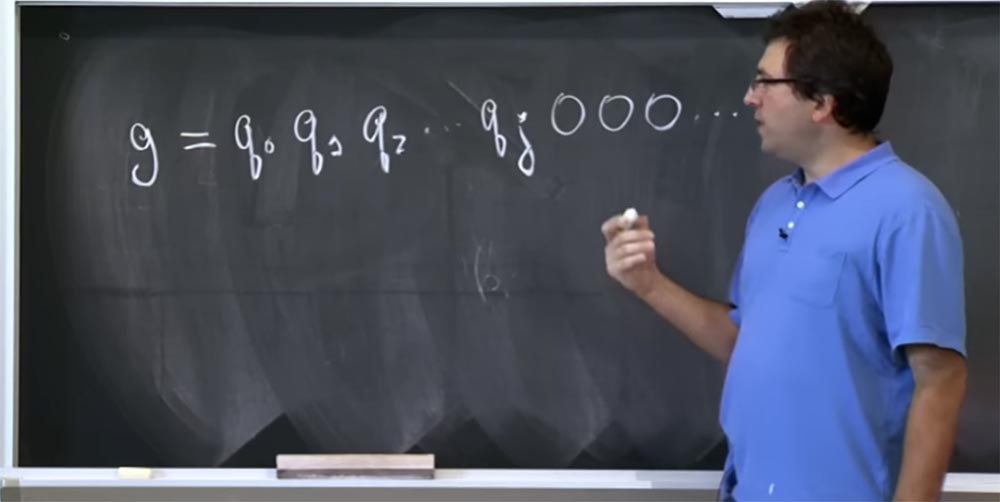
حاول هؤلاء الرجال حقن هذا التخمين ز في هذا المكان من خط الأنابيب لدينا: (c0 ') d mod q. لأن هذا هو المكان الذي يتم فيه استخدام نوعين من التحسين: طريقة Karatsub بدلاً من الضرب المعتاد وعدد مختلف من الاختصارات الإضافية اعتمادًا على قيمة c
0 '. في الواقع ، حاولوا إدخال تخمينين مختلفين في هذا المكان من خط الأنابيب: الأول ، الذي يبدو مثل g = q
0 q
1 q
2 ... qj 000 ... 0000 ، والثاني ، الذي أطلقوا عليه اسم g
high ، والذي يتكون من نفس البتات العالية ، ولكن بدلاً من ذلك من بين جميع الأصفار في النهاية هناك وحدة تدل على بت مرتفع ، تليها الأصفار مرة أخرى:
g = q
0 q
1 q
2 ... qj 100 ... 0000.
كيف يساعد هذا هؤلاء الرجال على فهم ما يحدث؟ هناك طريقتان للقيام بذلك. افترض أن تخميننا g يساوي القيمة c
0 '. يمكننا أن نفترض أن هذه g و g
high تتوافق مع القيمة c
0 'المعطاة على اللوحة اليسرى. في الواقع ، من السهل جدًا القيام بذلك لأن c
0 'من السهل جدًا حسابه عكسيًا من قيمة الإدخال المشفرة c
0 ، يمكنك فقط ضربه في R.
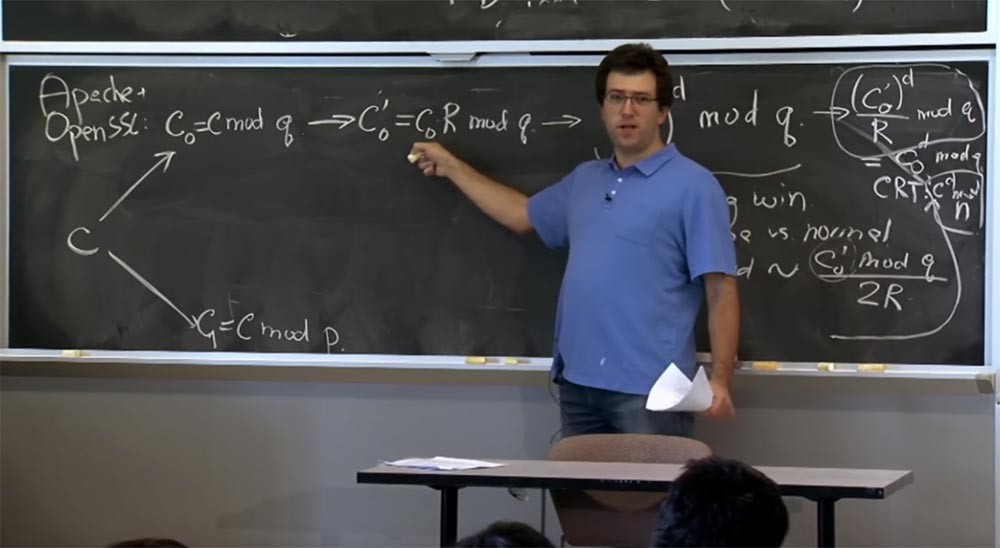
لذلك ، من أجل تخمين القيمة (c
0 ')
د ، يحتاجون فقط إلى تخمينهم ، تخمينهم g ، وتقسيمها أولاً على R ، أي قسمة 512 على شيء ما هناك. ثم سيقومون بتقديمه مرة أخرى ، سيقوم الخادم بضربه في R ومواصلة العملية الموضحة في مخطط خط الأنابيب الخاص بنا.
لذا ، لنفترض أننا تمكنا من وضع قيمة العدد الصحيح المحدد في المكان الصحيح. إذن ، ما هو وقت الحساب c
0 'إلى d mod q؟
هناك خياران محتملان حيث تتلاءم q مع هذه الصورة. قد يكون q بين هذين القيمتين g و g
high ، لأن البتة التالية من q هي 0. وبالتالي ، فإن هذه القيمة - أول 0 بعد qj - ستكون أقل من q ، لكن هذه القيمة - 1 بعد q - ستكون أكثر من س. يحدث هذا إذا كانت البتة التالية من q تساوي 0 ، أو من الممكن أن تكون q أعلى من كلتا القيمتين إذا كانت البتة التالية من q تساوي 1.
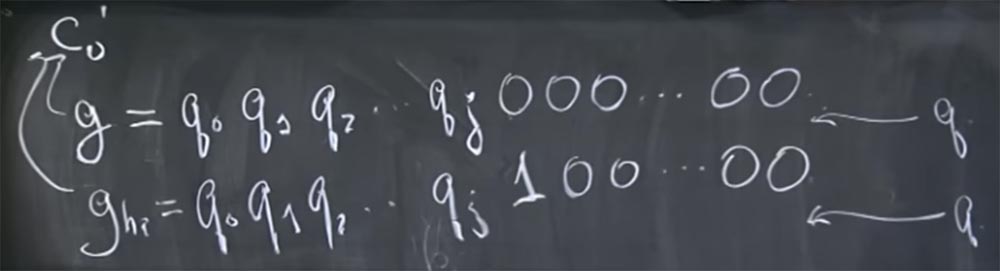
الآن يمكننا أن نقول ما سيكون وقت فك التشفير لهاتين القيمتين إذا كانت q تقع بينهما ، أو إذا كانت q تقع فوق كل منهما.
دعونا نلقي نظرة على الموقف حيث يقع q أعلاه. في هذه الحالة ، كل شيء هو نفسه إلى حد كبير. نظرًا لأن كلا من هذه القيم أقل من q ، فإن قيمة هذه الأشياء في mod q ستكون نفسها تقريبًا. وهي مختلفة قليلاً بسبب هذا الحجم الإضافي ، ولكنها لا تزال بنفس الحجم تقريبًا. وعدد التخفيضات الإضافية ، التخفيض الإضافي ، ربما لن يختلف كثيرًا أيضًا ، لأنه يتناسب مع قيمة c0 'mod q. وبالنسبة لكل من القيم
العالية g و g الأقل من q ، فكلها متشابهة. لن يتجاوز أي منها q ولن يتسبب في عدد كبير من التخفيضات الإضافية ، لأن q أكبر من هذين التخمينين ، سيظل عدد الحسابات باستخدام طريقة Karatsuba فيما يتعلق بعدد الحسابات العادية كما هو. فيما يتعلق بهذه العلاقة ، سيتعامل الخادم مع كل من g و g
عالية بالتساوي. لذلك ، فإن الخادم على وشك إجراء نفس المقدار من الاختصارات الإضافية لكل من هذه القيم. وبالتالي ، إذا رأيت أن الخادم يقضي نفس الوقت في الاستجابة لهذه التخمينات ، فمن المحتمل أن تفترض أن هناك بالفعل 1 في القيمة
العالية g في هذه المرحلة.
من ناحية أخرى ، إذا كانت q تقع بين هاتين القيمتين ، فهناك شيئان محتملان يمكن أن يتسببان في تغيرات التوقيت والتوقيت. أحد الأشياء هو أنه بما أن g
high أكبر قليلاً من q ، فإن عدد التخفيضات الإضافية سيكون متناسبًا مع c
0 'mod q ، وهو صغير جدًا لأن c
0 ' هو q بالإضافة إلى بعض البتات في تسلسل البت الإضافي هذا 100 ... 00. وبالتالي ، سيكون عدد التخفيضات الإضافية أكثر وضوحًا وسيبدأ كل شيء في حدوثه بشكل أسرع.
, , , , , : «, !». , g c
0 ' , q, , g
high q, g
high mod q . , . – , , .
c
0 ' mod q. c
0 g
high , q, , g q. , . , , . , 32- , .
, 32- , , , . , . 32 , , - . , , 32, , , , .
, , , . , q 1, , q 0, , g
high q , , .
. , . , . , , 1-2 . , , Ethernet.
, . . , 7 . , , -, , ?
: ?
: , , , , , . , .
, , 7 , , 7 . 7 g, 7 g + 1, g + 2 7 g + 400. g, g, , 7 400, ?
: , , ?
: , , , — (c
0 ')
d . . , , , mod p. , , . , g, 1, 2, 3, , .
, , – 100…00. , mod p, , mod p . « », , (c
0 ')
d , . ?
: , ?
: - , q. , q, , , .
: c
0 '?
: c
0 ', c, c
0 ' R mod n.
, «» , c
0 = mod q, c
0 = ((c
0 ' R
-1 ) mod n) mod q. R, R. c
0 ', (c
0 ')
d mod q. , , , , R. , R = 2
512 . , .
: mod p ?
: , , ? , ! , .
.
, . ? ? ,
30% entry-level , : VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps $20 ? ( RAID1 RAID10, 24 40GB DDR4).
VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps ,
.
Dell R730xd 2 ? فقط لدينا
2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV من 249 دولارًا في هولندا والولايات المتحدة!اقرأ عن كيفية بناء مبنى البنية التحتية الفئة c باستخدام خوادم Dell R730xd E5-2650 v4 بتكلفة 9000 يورو مقابل سنت واحد؟