ذات مرة تخرجت في الفيزياء. تعلمت لاحقًا بمفردي كمبرمج ويب. منذ ذلك الحين ، أعمل بشكل أساسي كمبرمج ، لكنني أستمر في تخصيص الوقت للفيزياء والتكنولوجيا (أحسب شيئًا ما أو أقوم ببنائه) ، والعلوم بشكل عام. مثل هذا "الانقسام" يجلب نتائج مثيرة للاهتمام. اتضح أن بعض الحقائق في الفيزياء يمكن شرحها جيدًا باستخدام البرمجة.
من أين أتى هذا السؤال؟ كان لدى أكبر طفل في المدرسة درسًا حول كواكب النظام الشمسي. بشكل عام ، يعرفهم ، وفي سماء المساء رأينا بعضًا (المشتري والمريخ وزحل). لكن العديد من الحقائق المثيرة للاهتمام ما زالت تفوق الفهم. قلة الرؤية والحركة وربما التفاعل. هذه الفجوة في عرض المواد بالتحديد هي التي أردت ملؤها بمساعدة برمجة الويب ، باتباع الحكمة المعروفة "من الأفضل أن ترى مرة واحدة من أن تسمع مائة مرة."
كما كنت قد خمنت ، ستركز المقالة على الحقائق المتعلقة بالنظام الشمسي (وليس الكواكب فقط). دعونا نرى ما هو الغريب في ركن المجرة.
لتوضيح كل شيء مكتوب ، قمت بإعداد عدد من صفحات الويب التي سأوفر روابط لها أثناء المحادثة. في هذه المقالة ، نستخدم حزمة
html + svg + javascript . إنه بسيط ومفهوم ومناسب تمامًا لأهدافنا. إذا كنت مهتمًا بكيفية عمل هذا أو ذاك "تحت الغطاء" ، فيمكنك فتح الرموز المصدر لصفحاتي والاطلاع عليها بأمان. يتم توفير روابط إلى ويكيبيديا أيضًا إذا كنت ترغب في القراءة عن شيء ما بمزيد من التفاصيل.
اللامركزية
يرتبط الافتراض الرئيسي عند إنشاء الصفحات بانحراف غريب الأطوار. توضح هذه المعلمة درجة استطالة المدار. إذا كان الانحراف صفرًا ، فهذه دائرة نظيفة ، إذا كانت من الصفر إلى الوحدة ، فإن القطع الناقص. يعرف الكثير من الناس أن مدار بلوتو بيضاوي الشكل بشكل واضح (حتى يتداخل جزئيًا مع مدار نبتون). لذا ، فإن الانحراف عنها هو 0.24. ما هو مثير للاهتمام ، اتضح ، وفي مدار عطارد اللامركزية 0.2. بالنسبة للكواكب الأخرى ،
تتراوح القيمة
من 0.01 إلى 0.1 .
من أجل عدم تعقيد الحسابات والجدول الزمني ، سننظر أيضًا
في المدارات ببساطة دائرية ، بما في ذلك الزئبق. سنستبعد بلوتو من الاعتبار ، لأنه يحتوي أيضًا على ميل للمدار - النموذج معقد للغاية. بالطبع ، يسمح لك svg برسم علامات الحذف ، ولكن المدارات الدائرية ستكون كافية بالنسبة لنا لفهم القضايا الأساسية ورسم في المتصفح.
هيكل النموذج
الآن يمكنك إنشاء كل ما تحتاجه على صفحتنا. هناك عنصر في svg يناسبنا فقط. مع ذلك ، يمكنك رسم الشمس ، والكواكب ، ومداراتها. يتم حساب موقع الشمس والكواكب ، بالإضافة إلى أحجام المدارات ، باستخدام جافا سكريبت بناءً على الحجم الحالي لنافذة المتصفح (عذرًا ، ولكن في متصفحات الجوال ، ربما تكون صغيرة جدًا). للعرض ، يتم حساب مقياس بحيث يناسب أكبر مدار في الشاشة. لحساب الموقع الحالي للكوكب ، تم أخذ فترة ثورته حول الشمس في سنوات الأرض.
كواكب مجموعة الأرض
دعنا نبدأ. الجزء الأول ، هناك
أربعة كواكب داخلية على المسرح. في هذه الصفحة ، قمنا "باختبار" بنية html و svg بحيث لا يتحرك أي شيء في أي مكان ، وقم بتصحيح جافا سكريبت. من المهم القيام بكل شيء نوعيًا ، حتى تستخدم جميع الصفحات التالية نفس "الإطار".
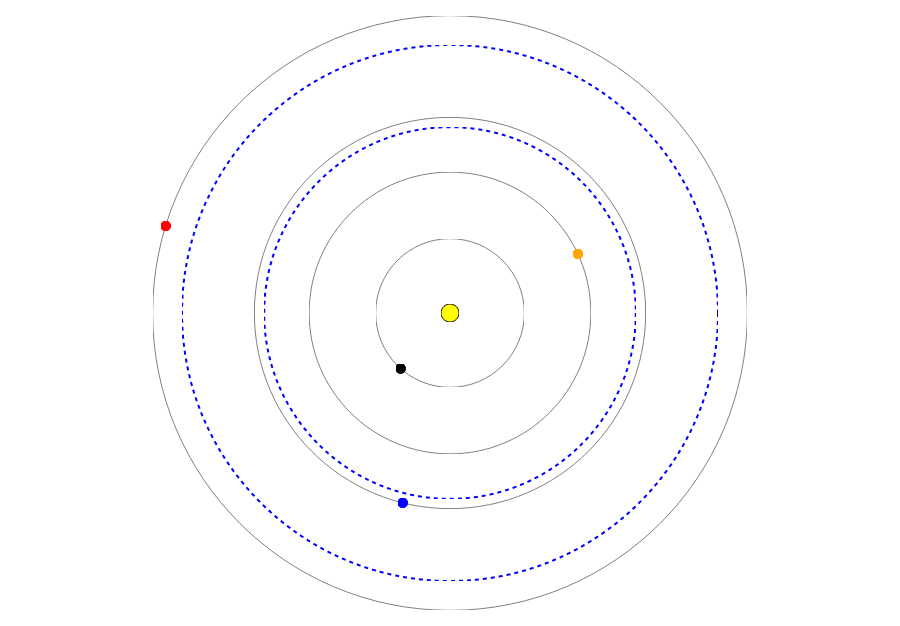
لذلك تم عمل كل شيء ، والكواكب تتحرك. الآن يمكنك إلقاء نظرة على النتائج المتعلقة على وجه التحديد بالفيزياء (علم الفلك). أولاً ، أصبحت العلاقات بين أحجام المدارات ، وثانياً ، بين فترات الثورة ، واضحة. لاحظ مدى سرعة مقارنة الزئبق بالأرض أو المريخ.
تحد دائرتان منقطتان في الرسوم المتحركة ما يسمى
بالمنطقة الصالحة للسكن حيث الحياة ممكنة. كما تخبرنا ويكيبيديا ، يقدم العلماء
المختلفون تقديرات مختلفة قليلاً لحدودها . أخذنا النطاق 0.95 - 1.37 AU تظهر الرسوم المتحركة بوضوح كم نحن محظوظون ، أبناء الأرض - كوكبنا هو الوحيد الذي دخل المنطقة الصحيحة.
ننتقل.
حزام الكويكبات
الجزء الثاني -
نفس المشتري على المسرح.
بالمقارنة مع الرسوم المتحركة الأولى هنا ، قمنا بتسريع الحركة 15 مرة - فقط حتى يكون للمشتري سرعة لائقة أكثر أو أقل (وإلا فإنه من المستحيل تمامًا الانتظار حتى يحدث ثورة واحدة على الأقل). يوضح هذا الفارق الدقيق
مدى بطء تحرك الكواكب الخارجية مقارنة بالكواكب الداخلية - كل ثورة حول الشمس بدأت بالفعل تصل إلى عشرات ومئات السنين.
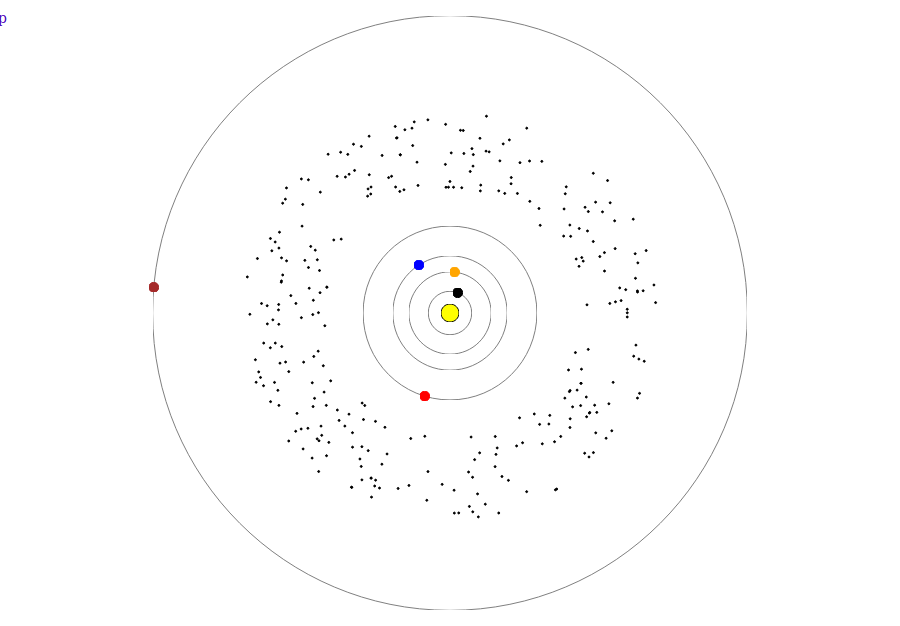
بالطبع ، الفجوة الهائلة بين مداري المريخ والمشتري مدهشة. في الواقع ، هناك
حزام من الكويكبات - الأشياء التي لا يمكن أن تشكل كوكبًا بسبب تأثير الجاذبية للمشتري. يمتد الحزام من 2.2 إلى 3.6 AU يظهر كل هذا "هراء البناء" المتبقي منذ بداية النظام الشمسي في الرسوم المتحركة بنقاط سوداء. بالطبع ، عليك أن تفهم أن هذا رسم تقريبي. لذلك ، هناك حوالي 300 ألف قطعة حقيقية في الحزام ، تظهر الرسوم المتحركة 300 مرتبة بشكل عشوائي - فقط لفهم الجوهر.
الرنين المداري
الجزء الثالث - إزالة الكواكب الصغيرة
وإضافة كوكب زحل إلى المشتري .
إن أكبر كوكبين ، مهما قلت ، يستحقان اهتمامًا خاصًا. لديهم
صدى مداري واضح - وهو الوضع الذي ، بسبب تفاعل الجاذبية ،
ترتبط فترات
دورانهم بأعداد طبيعية صغيرة . على وجه التحديد ، بالنسبة لزوج المشتري وزحل ، فإن نسبة الفترات هي 5: 2 (أي أن زحل يقوم بدورتين من خمس دورات للمشتري).
نوضح هذه الظاهرة باستخدام الرسوم المتحركة. لنقم بعمل تقسيم منفصل على الصفحة ، حيث سنضع علامة رأسية لكل ثورة لكل ثورة. سترتفع علامات المشتري (البني) في الأعلى ، وزحل (الأزرق) أدناه. يتم أيضًا رسم العلامات باستخدام svg.

إذا بدأنا الرسوم المتحركة ، فسوف نرى اختلافًا تدريجيًا في التسميات. في الواقع ، هذه هي النتيجة الحقيقية: عند قراءة نفس ويكيبيديا ، لسبب ما ، في عبارة "5: 2 تقريبًا" ، نتجاهل كلمة "تقريبًا". ونعتقد أن النظام الشمسي يشبه عمل الساعة مع تروس مجهزة بشكل مثالي. لكن العالم الحقيقي لا يزال أكثر تعقيدًا. ومن هنا كان التناقض.
الكواكب العملاقة
الجزء الرابع -
عمالقة الغاز على المسرح (المشتري وزحل وأورانوس ونبتون).
كما نرى ، فإن مدارات الكواكب تصبح أكبر ، والسرعات المدارية أصغر. مقارنة بالرسوم المتحركة الأولى ، يتم تسريع الوقت بالفعل 150 مرة (!) - بحيث كل شيء "يتنفس" أكثر أو أقل.
في هذا الجزء ، سنتحدث عن المذنبات ، خاصة أنها مرتبطة فقط بالكواكب العملاقة. يقسم علماء الفلك المذنبات إلى فترات قصيرة وطويلة (الفترة الأولى للدوران أقل من 200 سنة ، والثانية ، على التوالي ، أكثر من 200). علاوة على ذلك ، تنقسم الفترة القصيرة بدورها إلى
عائلات مكونة
من أربعة كواكب فقط - عائلة المشتري وزحل وأورانوس ونبتون. هذا يرجع إلى أي الكواكب لها أكبر تأثير على مذنب معين. بطبيعة الحال ، توجد الكثير من المواد عن المذنبات على ويكيبيديا ، كما وجدت
مقالًا جيدًا عن حبري.
لفهم أفضل للعائلات ، نفرض الرسوم المتحركة على المدار لزوج من بعض المذنبات. فليكن ، على سبيل المثال ،
المذنب هالي (المدار الأحمر)
والمذنب إنكه (المدار البنفسجي) - أول ما تمكن العلماء من حساب معلمات الحركة من أجله.

من أجل التقديم الصحيح للعلامات الناقصة في svg ، كان علي أن أجلس قليلاً بقلم رصاص وورقة وحساب نصف محاور واحد أو المدار الآخر. بالطبع ، لا أعرف الاتجاه المحدد للحذف ، لذلك يتم توجيهها إلى اليسار فقط. ومع ذلك ، أصبح من الواضح الآن بوضوح لماذا يُنسب المذنب Encke إلى عائلة المشتري ، وهالي إلى عائلة نبتون: "يصل" الأول فقط إلى مدار المشتري ، والثاني ، على التوالي ، نبتون (إذا أردت ، يمكنك "اللعب" مع نفسك باستخدام الكود ، واستبدال أي مذنبات أخرى من هذه أو من عائلات أخرى - سيتم رؤيته حيث تصل المدارات).
جميع الكواكب وما بعدها
لذا ، في أربعة رسوم متحركة ، نظرت أنا وأنت إلى جميع الأشياء الرئيسية الموجودة في النظام الشمسي - الكواكب والكويكبات والمذنبات والمناطق والأحزمة. يبقى لمناقشة هذا
الأخير .
الصورة العامة مثيرة للاهتمام من حيث أنها توضح مدى صغر مساحة نظامنا التي درسناها وأتقنناها. إن الدائرة المألوفة للكواكب الداخلية ليست سوى "رقعة" مجهرية في المركز. إن مدار نبتون هو الحدود التالية ، أبعد بكثير. وحولها - حزام كويكتر عملاق -
حزام كويبر ، والذي يحده خطوط متقطعة.

أود أن أصدق أن تطلعات البشرية لن تظل محدودة بتلك الجزيرة الصغيرة ، التي يحددها مدار المريخ. حتى صفحة html البسيطة هذه تقول أنه لا يزال أمامنا الكثير من الأشياء الأكثر إثارة للاهتمام.