
نعزز مهارات حل المعادلات التفاضلية وتصورها باستخدام واحدة من أكثر المعادلات التطورية شيوعًا كمثال ، وتذكر Scilab القديم الجيد ومحاولة فهم ما إذا كنا بحاجة إليه ... تحت الصورة المقطوعة (كيلو بايت لسبعمائة)
تأكد من أن البرنامج جديدjulia>] (v1.0) pkg>update
دعنا نذهب من خلال أدلة الماضي
وانتقل إلى بيان المشكلة
حركة الجسيمات المشحونة في المجال الكهرومغناطيسي
على جسيم مشحون بشحنة q تتحرك في EMF بسرعة u تعمل قوة لورنتز: vecFL=q left( vecE+ left[ vecu times vecB right] right) . هذه الصيغة صالحة مع عدد من التبسيط. بإهمال التصحيحات على نظرية النسبية ، نعتبر كتلة الجسيمات ثابتة ، وبالتالي فإن معادلة الحركة لها الشكل: fracddt(m vecu)=q left( vecE+ left[ vecu times vecB right] right)
دعونا نوجه المحور Y على طول المجال الكهربائي ، المحور Z على طول المجال المغناطيسي ، ونفترض البساطة أن سرعة الجسيمات الأولية تكمن في المستوى XY. في هذه الحالة ، فإن المسار الكامل للجسيم سيقع أيضًا في هذا المستوى. تأخذ معادلات الحركة الشكل التالي:
\ left \ {\ start {matrix} m \ ddot {x} = qB \ dot {y} \\ m \ ddot {y} = qE-qB \ dot {x} \ end {matrix} \ right.
\ left \ {\ start {matrix} m \ ddot {x} = qB \ dot {y} \\ m \ ddot {y} = qE-qB \ dot {x} \ end {matrix} \ right.
لا حد لها: x∗= fracx lambda، ،y∗= fracy lambda، ، tau= fracct lambda، ،B∗= fracBmcq lambda، ،E∗= fracEmc2q lambda . تشير العلامات النجمية إلى كميات الأبعاد ، و lambda - الحجم المميز للنظام المادي المعتبر. نحصل على نظام بلا أبعاد لمعادلات حركة الجسيمات المشحونة في المجال المغناطيسي:
\ left \ {\ start {matrix} \ frac {d ^ 2x} {d \ tau ^ 2} = B \ frac {dy} {d \ tau} \\ \ frac {d ^ 2y} {d \ tau ^ 2} = EB \ frac {dx} {d \ tau} \ end {matrix} \ right.
\ left \ {\ start {matrix} \ frac {d ^ 2x} {d \ tau ^ 2} = B \ frac {dy} {d \ tau} \\ \ frac {d ^ 2y} {d \ tau ^ 2} = EB \ frac {dx} {d \ tau} \ end {matrix} \ right.
لنخفض الترتيب:
\ left \ {\ start {matrix} \ frac {dx} {d \ tau} = U_x \\ \ frac {dy} {d \ tau} = U_y \\ \ frac {dU_x} {d \ tau} = BU_y \\ \ frac {dU_y} {d \ tau} = E-BU_x \ end {matrix} \ right.
\ left \ {\ start {matrix} \ frac {dx} {d \ tau} = U_x \\ \ frac {dy} {d \ tau} = U_y \\ \ frac {dU_x} {d \ tau} = BU_y \\ \ frac {dU_y} {d \ tau} = E-BU_x \ end {matrix} \ right.
كتكوين أولي للنموذج ، نختار: B=2 ت E=5 cdot104 V / م v0=7 cdot104 م / ث بالنسبة للحل العددي ، نستخدم حزمة التفاضلية :
الرمز والرسومات using DifferentialEquations, Plots pyplot() M = 9.11e-31
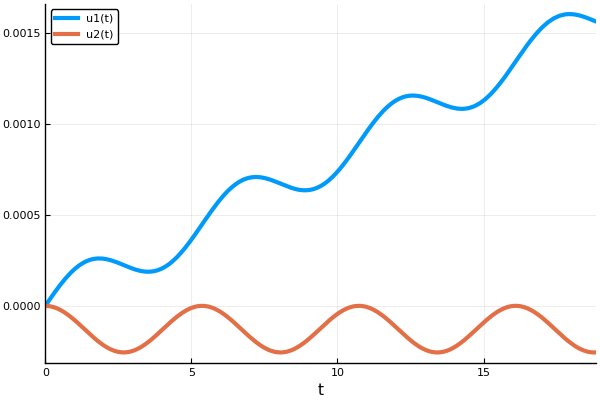
هنا نستخدم طريقة أويلر ، والتي يتم تحديد عدد الخطوات لها. أيضا ، لا يتم حفظ الحل الكامل للنظام في مصفوفة الإجابات ، ولكن فقط 1 و 2 من المؤشرات ، أي إحداثيات X واللاعب (لا نحتاج إلى سرعات).
X = [Solut.u[i][1] for i in eachindex(Solut.u)] Y = [Solut.u[i][2] for i in eachindex(Solut.u)] plot(X, Y, xaxis=("X"), background_color=RGB(0.1, 0.1, 0.1)) title!(" ") yaxis!("Y") savefig("XY1.png")

تحقق من النتيجة. نقدم متغير جديد بدلاً من x tildex=x−ut . وبالتالي ، يتم الانتقال إلى نظام إحداثيات جديد يتحرك بالنسبة إلى الأصل بسرعة u في اتجاه المحور X :
\ left \ {\ start {matrix} \ ddot {\ tilde {x}} = qB \ dot {y} / m \\ \ ddot {y} = qE / m-qB \ dot {x} / m -qBu / m \ end {matrix} \ right.
\ left \ {\ start {matrix} \ ddot {\ tilde {x}} = qB \ dot {y} / m \\ \ ddot {y} = qE / m-qB \ dot {x} / m -qBu / m \ end {matrix} \ right.
إذا اخترت u=E/B والدلالة omega=qB/m ثم يتم تبسيط النظام:
\ left \ {\ start {matrix} \ ddot {\ tilde {x}} = \ omega \ dot {y} \\ \ ddot {y} = - \ omega \ dot {\ tilde {x}} \ end { مصفوفة} \ حق.
\ left \ {\ start {matrix} \ ddot {\ tilde {x}} = \ omega \ dot {y} \\ \ ddot {y} = - \ omega \ dot {\ tilde {x}} \ end { مصفوفة} \ حق.
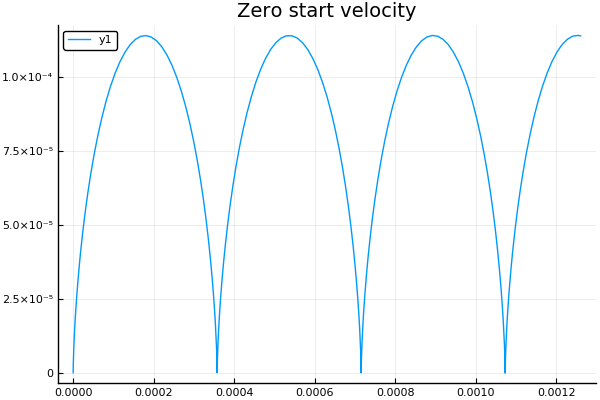
اختفى المجال الكهربائي من آخر التساوي ، وهي معادلات حركة الجسيمات تحت تأثير المجال المغناطيسي المنتظم. وبالتالي ، يجب أن يتحرك الجسيم في نظام الإحداثيات الجديد (س ، ص) في دائرة. نظرًا لأن نظام الإحداثيات الجديد هذا يتحرك نسبيًا مع الأصل بسرعة u=E/B ، ثم تتكون حركة الجسيمات الناتجة من حركة موحدة على طول المحور X والدوران حول الدائرة في المستوى XY . كما تعلمون ، فإن المسار الذي يحدث عندما يتم الجمع بين هاتين الحركتين معًا هو بشكل عام حلقي . على وجه الخصوص ، إذا كانت السرعة الأولية صفرًا ، يتم تحقيق أبسط حالة حركة من هذا النوع - على طول دائرية .
دعونا نتأكد من أن سرعة الانجراف تساوي حقًا E / V. للقيام بذلك:
- سنفسد مصفوفة الاستجابة عن طريق تعيين قيمة أقل عمداً بدلاً من العنصر الأول (الحد الأقصى)
- نجد عدد الحد الأقصى للعنصر في العمود الثاني من مصفوفة الاستجابة ، والذي يتأخر بالإحداثيات
- نحسب سرعة الانجراف بلا أبعاد من خلال قسمة الحد الأقصى لقيمة الهوامش على القيمة الزمنية المقابلة
Y[1] = -0.1 numax = argmax( Y ) X[numax] / Solut.t[numax]
خارج: 8.334546850446588e-5
B = 2*q*λ / (M*C) E = 5e4*q*λ / (M*C*C) E/B
خارج: 8.33333333333333332e-5
حتى الترتيب السابع!
من أجل الراحة ، نحدد وظيفة تأخذ معلمات النموذج وتوقيع الرسم البياني ، والتي ستكون بمثابة اسم ملف png الذي تم إنشاؤه في مجلد المشروع (يعمل في Juno / Atom و Jupyter). على عكس Gadfly ، حيث تم إنشاء الرسوم البيانية في طبقات ثم عرضها بواسطة وظيفة plot () ، في Plots ، من أجل إنشاء رسوم بيانية مختلفة في إطار واحد ، يتم إنشاء أولها بواسطة وظيفة plot () ، ويتم إضافة الرسوم اللاحقة باستخدام المخطط! () . من المعتاد أن تنتهي أسماء الدوال التي تغير الكائنات المقبولة في جوليا بعلامة تعجب.
function plotter(ttle = "qwerty", Bo = 2, Eo = 4e4, vel = 7e4) Ans = modelsolver(Bo, Eo, vel) X = [Ans.u[i][1] for i in eachindex(Ans.u)] Y = [Ans.u[i][2] for i in eachindex(Ans.u)] plot!(X, Y) p = title!(ttle) savefig( p, ttle * ".png" ) end
عند السرعة الأولية الصفرية ، كما هو متوقع ، نحصل على دائرية :
plot() plotter("Zero start velocity", 2, 4e4, 7e4)
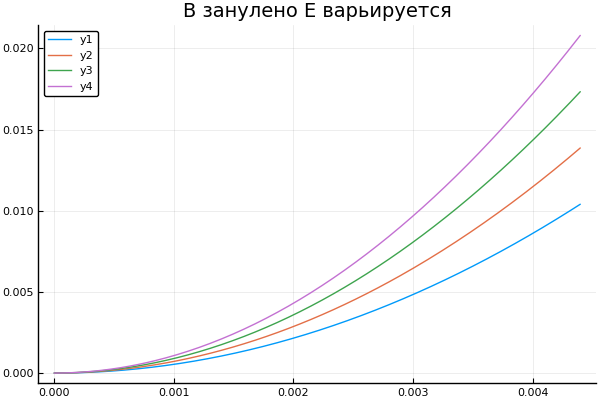
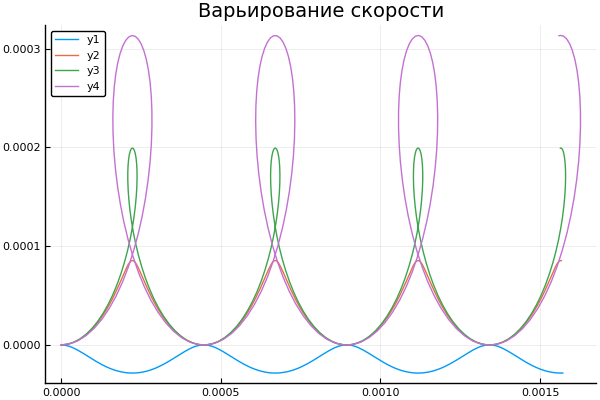
نحصل على مسار الجسيم عند الحث والشدة وعندما تتغير علامة الشحن. دعني أذكرك بأن النقطة تعني التنفيذ المتسلسل لوظيفة مع جميع عناصر المصفوفة
مطوي بعيدا plot() plotter.("B ", 0, [3e4 4e4 5e4 6e4] )
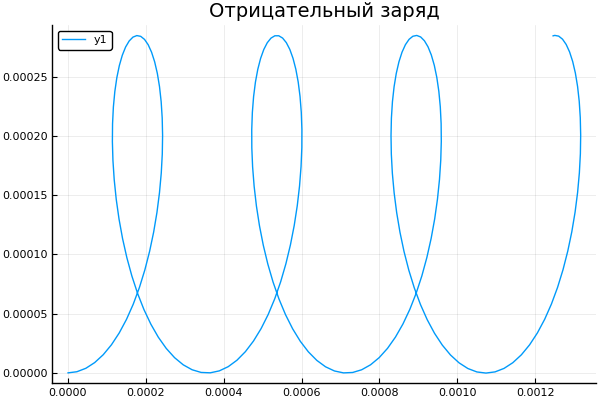
plot() plotter.("E B ", [1 2 3 4], 0 )

q = -1.6e-19
ودعنا نرى كيف يؤثر التغيير في السرعة الأولية على مسار الجسيم: plot() plotter.(" ", 2, 5e4, [2e4 4e4 6e4 8e4] )
قليلا عن Scilab
في حبري ، هناك بالفعل معلومات كافية حول Silab ، على سبيل المثال 1 ، 2 ، وهنا حول Octave ، لذلك سنقتصر على الروابط إلى ويكيبيديا والصفحة الرئيسية .
بمفردي ، سأضيف عن وجود واجهة ملائمة مع مربعات اختيار وأزرار ورسوم بيانية وأداة Xcos النمذجة المرئية المثيرة للاهتمام إلى حد ما. يمكن استخدام هذا الأخير ، على سبيل المثال ، لمحاكاة إشارة في الهندسة الكهربائية:
في الواقع ، يمكن أيضًا حل مهمتنا في Scilab:
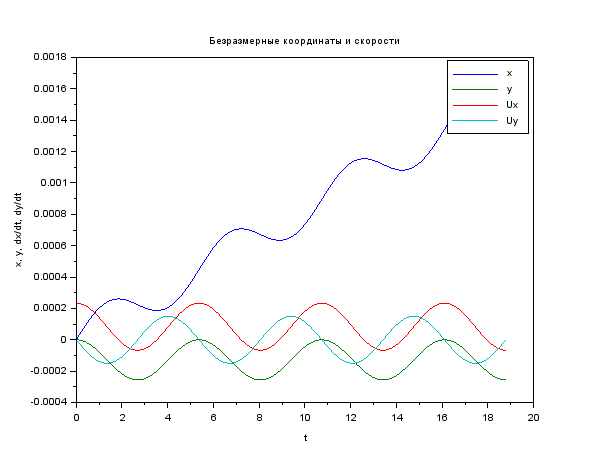
الرمز والصور clear function du = syst(t, u, A, E) du = A * u + [0; 0; 0; E] // ODE system endfunction function [tspan, U] = modelsolver(Bo, Eo, vel) B = Bo*q*lambda / (M*C) E = Eo*q*lambda / (M*C*C) vel = vel / C u0 = [0; 0; vel; 0] // start cond-ns t0 = 0.0 tspan = t0:0.1:6*%pi // time period A = [0 0 1 0; 0 0 0 1; 0 0 0 B; 0 0 -B 0] U = ode("rk", u0, t0, tspan, list(syst, A, E) ) endfunction M = 9.11e-31 // kg q = 1.6e-19 // C C = 3e8 // m/s lambda = 1e-3 // m [cron, Ans1] = modelsolver( 2, 5e4, 7e4 ) plot(cron, Ans1 ) xtitle (" ","t","x, y, dx/dt, dy/dt"); legend ("x", "y", "Ux", "Uy"); scf(1)// plot(Ans1(1, :), Ans1(2, :) ) xtitle (" ","x","y"); xs2png(0,'graf1');// xs2jpg(1,'graf2');// , -

هنا معلومات عن وظيفة حل ode يختلف . من حيث المبدأ ، يطرح السؤال
لماذا نحتاج جوليا؟
... إذا كانت هناك أشياء رائعة مثل Scilab و Octave و Numpy ، Scipy؟
حول الأخيرين لن أقول - لم أحاول ذلك. بشكل عام ، السؤال معقد ، لذلك دعونا نلقي نظرة سريعة:
شيلاب
على محرك الأقراص الثابتة ، سيستغرق الأمر أكثر من 500 ميغابايت ، ويبدأ بسرعة وعلى الفور هناك حساب تفاضلي متاح ورسومات وكل شيء آخر. جيد للمبتدئين: دليل ممتاز (مترجم في الغالب) ، هناك العديد من الكتب باللغة الروسية. لقد قيل بالفعل عن الأخطاء الداخلية هنا وهنا ، وبما أن المنتج مناسب للغاية ، فإن المجتمع بطيئ ، والوحدات الإضافية نادرة جدًا.
جوليا
مع إضافة الحزم (خاصة أي بايثون-لا جوبيتر وماثبلوتليب) ، تنمو من 376 ميجا بايت إلى ما يزيد قليلاً عن ستة غيغابايت. كما أنها لا توفر ذاكرة الوصول العشوائي: في بداية 132 ميجابايت وبعد تخطيط الجداول في المشتري ، ستصل بهدوء إلى 1 جيجابايت. إذا كنت تعمل في Juno ، فكل شيء يشبه تقريبًا في Scilab : يمكنك تنفيذ التعليمات البرمجية على الفور في المترجم ، ويمكنك الطباعة في المفكرة المدمجة وحفظها كملف ، وهناك متصفح متغير ، وسجل أوامر ، ومساعدة عبر الإنترنت. أنا شخصياً ساخط على عدم وضوح () ، أي أنني أطلقت الرمز ، ثم بدأت في تصحيحه وإعادة تسميته ، وبقيت المتغيرات القديمة (لا يوجد متصفح متغير في المشتري).
لكن كل هذا ليس بالغ الأهمية. Scilab مناسب تمامًا للزوجين الأولين ، حيث يعد صنع الجبين أو المؤشر أو حساب شيء بينهما أداة مرتجلة للغاية. على الرغم من وجود دعم أيضًا للحوسبة المتوازية واستدعاء وظائف sishn / Fortran ، والتي لا يمكن استخدامها بجدية. المصفوفات الكبيرة ترعبه ، لوضع مجموعات متعددة الأبعاد ، يجب عليك التعامل مع جميع أنواع الظلامية ، والحسابات التي تتجاوز نطاق المهام الكلاسيكية قد تسقط كل شيء مع نظام التشغيل.
وبعد كل هذه الآلام وخيبات الأمل ، يمكنك التبديل بأمان إلى جوليا لأخذها هنا أيضًا. سنستمر في الدراسة ، وفائدة المجتمع متجاوبة للغاية ، وحل المشكلات بسرعة ، ولدى جوليا العديد من الميزات الأكثر إثارة للاهتمام التي ستحول عملية التعلم إلى رحلة مثيرة!