عمليات الموجة في الخطوط الهيدروليكية. الأساسيات

مرحبا يا هبر!

تحدثت في مقال سابق عن طريقة الخصائص ، المصممة لحساب عمليات الموجة في الخطوط الهيدروليكية. في الواقع ، بالطبع ، يمكن حساب العمليات الموجية في العقل ، ما عليك سوى معرفة النهج.

تحت القطع ، سوف أعرض "على الأصابع" وبمساعدة صور متحركة تأثيرات الموجة الرئيسية. كمثال ، سأستخدم الخط الهيدروليكي مرة أخرى ، ولكن في الواقع ، فهي تستند إلى نفس المعادلات تقريبًا كما في الصوتيات والخطوط الكهربائية. لذلك ، حتى إذا لم تكن هيدروليكيًا ، فقد تكون هناك تشابهات بسيطة لمساعدتك على فهم عمليات الموجة بشكل عام.

تحذير صور متحركة من تحت القط 15 MB!

لذا ، سننظر هنا في انتشار موجات مستوية أحادية البعد في خط هيدروليكي. هذا الافتراض صحيح تمامًا لخطوط الأنابيب الطويلة ، التي يزيد طولها عدة مرات عن القطر الداخلي. من أجل البساطة ، نتجاهل الاحتكاك في الوقت الحالي. في هذه الحالة ، سيتم وصف العمليات الفيزيائية الجارية من خلال زوج من المعادلات التفاضلية الجزئية:

$$

$$\ frac {\ جزئي p} {\ جزئي t} + \ rho \؛ c ^ 2 \ frac {\ جزئي v} {\ جزئي x} = 0$$

$$

$$\ frac {\ جزئي v} {\ جزئي t} + \ frac1 \ rho \ frac {\ displaystyle \ جزئي p} {\ displaystyle \ جزئي x} = 0$$

أين $$$\ rho$- الكثافة $$$v$- السرعة $$$p$- الضغط $$$c$- سرعة الصوت.

بدافع هذه العادة ، قد تبدو هذه المعادلات مخيفة ، ولكن في الواقع ، كل شيء بسيط هنا. تخبرنا المعادلة الأولى أن الضغط سيزداد بمرور الوقت إذا تدفق المزيد من السائل إلى جزء الأنبوب أكثر من تدفقه (علاوة على ذلك ، كلما كان السائل أكثر كثافة ومرونة في الأنبوب) ؛ تظهر المعادلة الثانية أنه من أجل تسريع جزء من السائل ، من الضروري تطبيق فرق ضغط عليه (علاوة على ذلك ، كلما زادت الكثافة ، يجب تطبيق فرق ضغط أكبر لتسريع القطعة). أي يتم وصف الأشياء العادية تمامًا: السائل قابل للانضغاط ، السائل له كتلة.
دعونا نترك الحل التحليلي لهذه المعادلات للمقالات المستقبلية ؛ فلننتقل فورًا إلى المثال "على الأصابع".
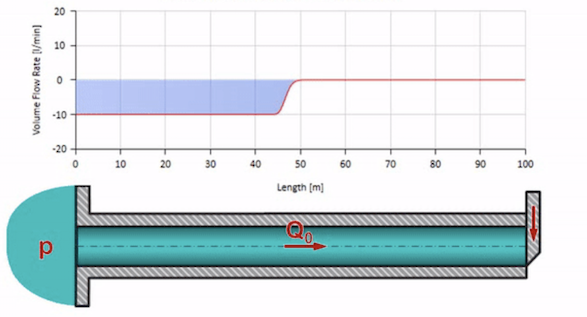
خذ أنبوبًا مملوءًا بالماء حيث يتم الحفاظ على ضغط 100 بار (10 ميجا باسكال) ومعدل تدفق 30 لتر / دقيقة. إذا تم تطبيق خطوة ضغط على الطرف الأيسر ، فمن المتوقع أن تبدأ في التحرك على طول التيار بسرعة مساوية لسرعة الصوت في الوسط.

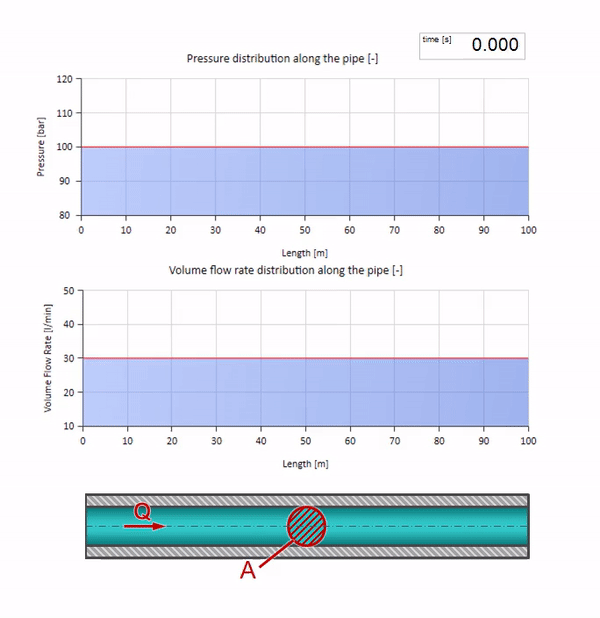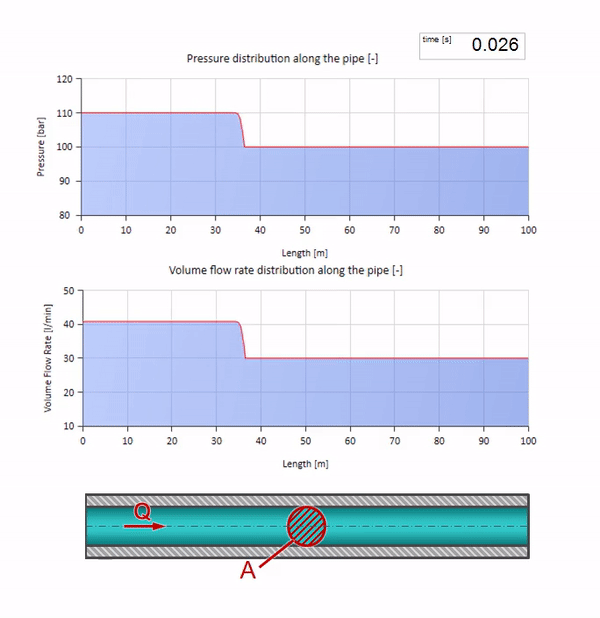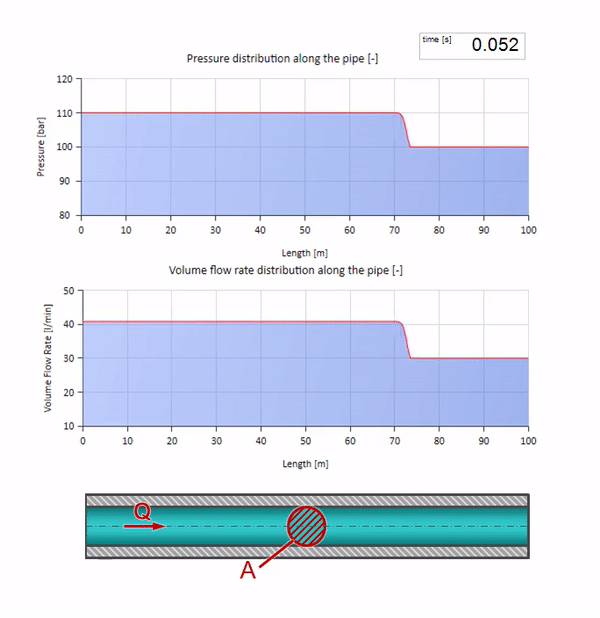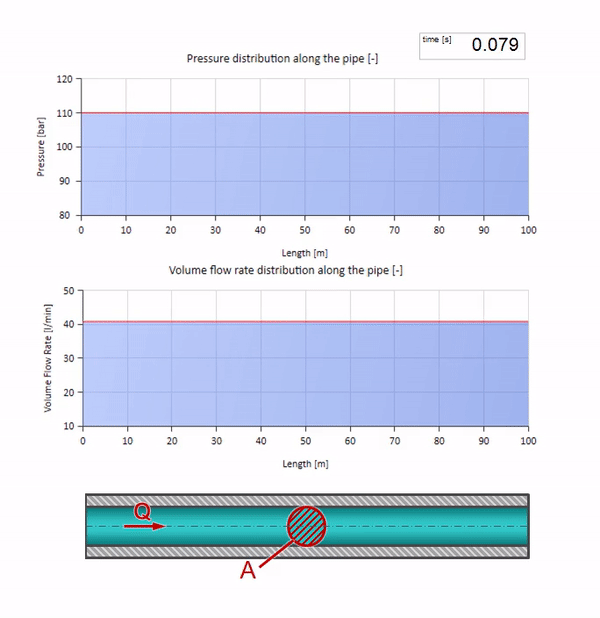
بالطبع ، مع الضغط ، سيتغير معدل التدفق أيضًا. إذا ارتفع الضغط ، فسوف "يضبط" السائل في اتجاه التيار ويزيد معدل التدفق ببعض "الخطوة" أيضًا. كم يتحدد بقيمة مقاومة الموجة. لأنبوب بمساحة مستعرضة $$$A$مليئة بالسائل بالكثافة $$$\ rho$وسرعة الصوت المحلية $$$c$، يمكن حساب مقاومة الموجة على النحو التالي:

$$

$$Z_L = \ frac {\ rho \؛ c} A$$

من حيث الأبعاد ، هذه هي نفس المقاومة الهيدروليكية التقليدية ، تستخدم فقط لحساب نسب موجة الضغط ( $$$\ widehat p$) ومعدل التدفق ( $$$\ واسع Q$) ، وليس قيمها المطلقة:

$$

$$Z_L = \ frac {\ widehat p} {\ widehat Q}$$

كلما زادت كثافة الصوت وسرعته ، زادت مقاومة الموجة ، أي كلما كان من الصعب انخفاض ضغط معين لتفريق السائل (زيادة التدفق)

الآن دعونا نرى كيف ستتحرك موجتان ، وتتحرك تجاه بعضها البعض:

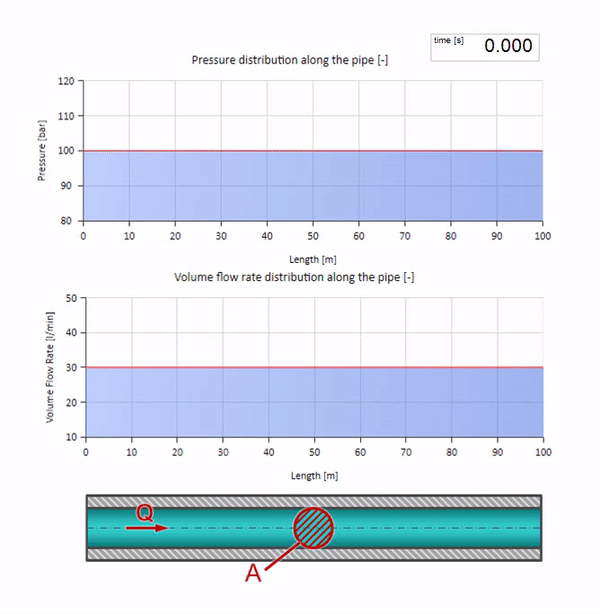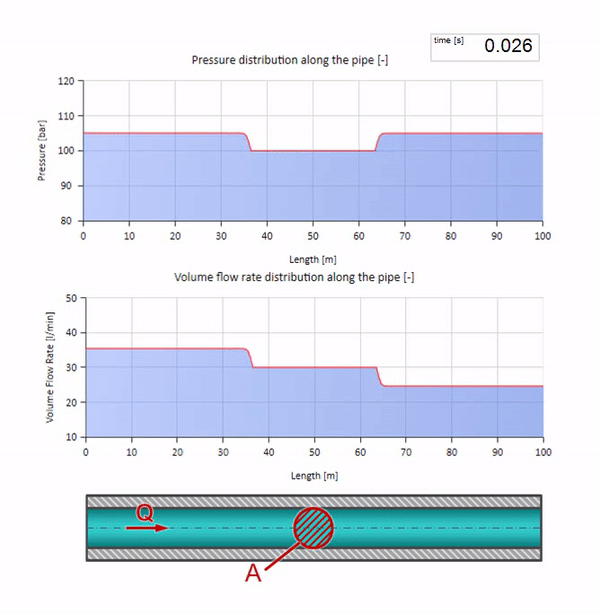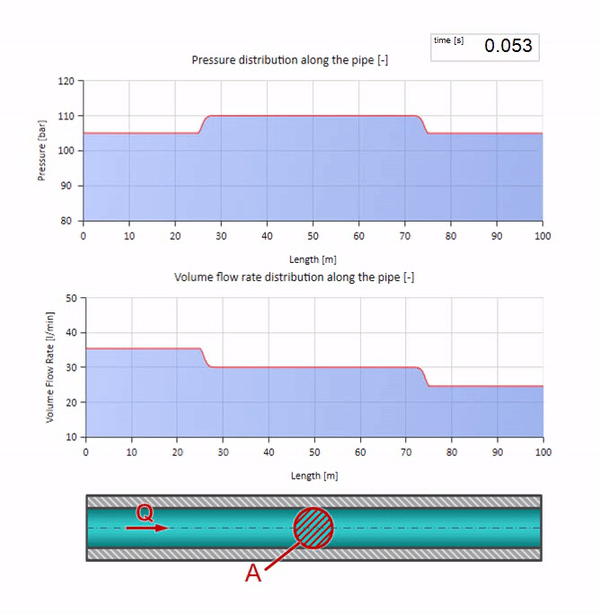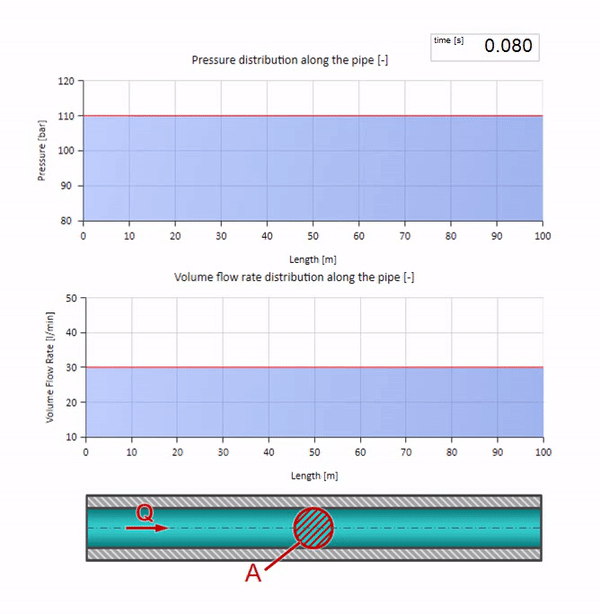
إذا ارتفع الضغط في الطرف الأيمن ، فسيتم إعاقة السوائل حتمًا بفرق سلبي. وهذا يعني أن موجة زيادة الضغط التي تسير ضد التدفق ستؤدي إلى انخفاض في معدل التدفق بمقدار محدد مرة أخرى بواسطة مقاومة الموجة. أي أن موجة نمو الضغط وتدفق السقوط ستتحرك إلى اليمين.
في التصادم ، قد يبدو أن موجات التدفق تنعكس من بعضها البعض وتعود. في الواقع ، هم ببساطة يتداخلون. يسمى هذا التأثير أيضًا التداخل:

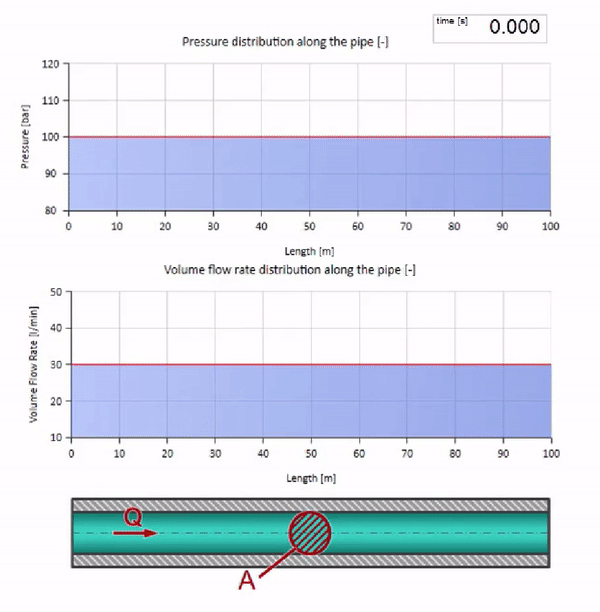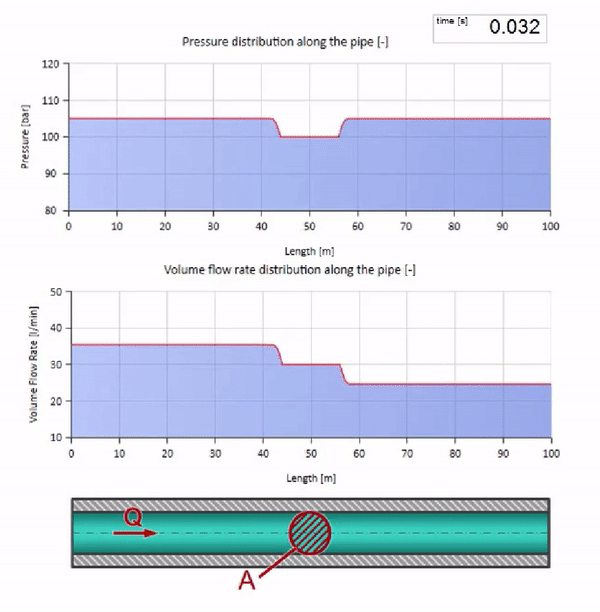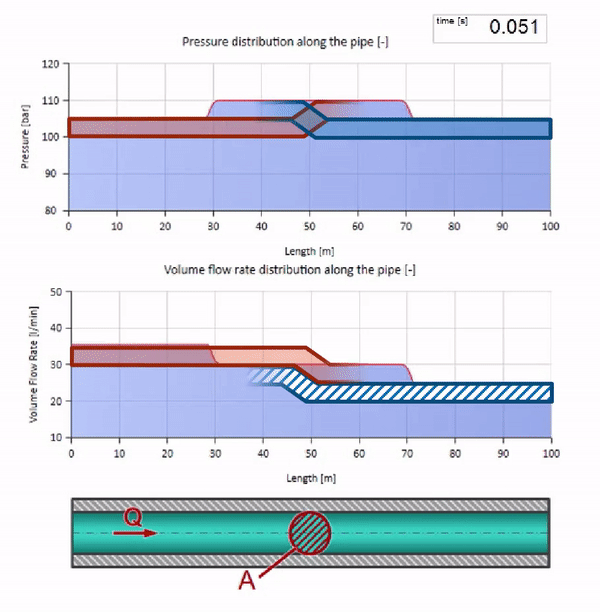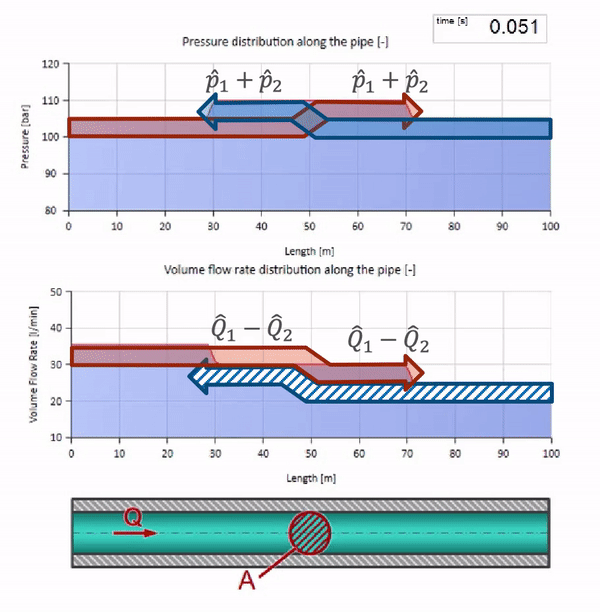
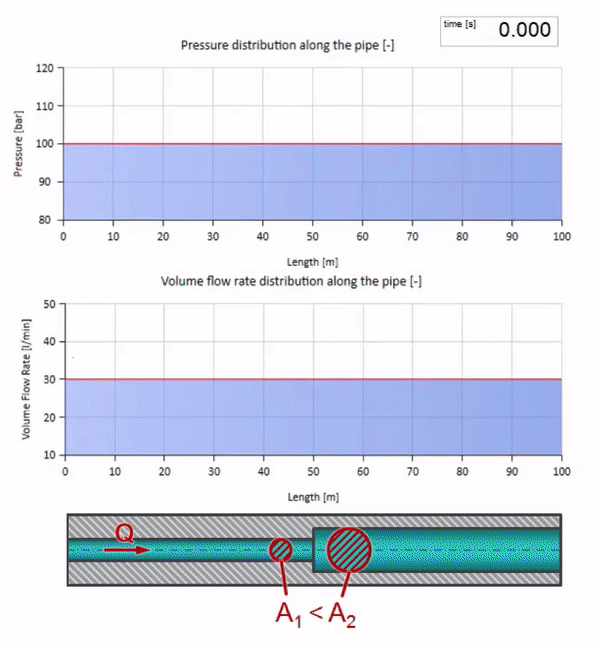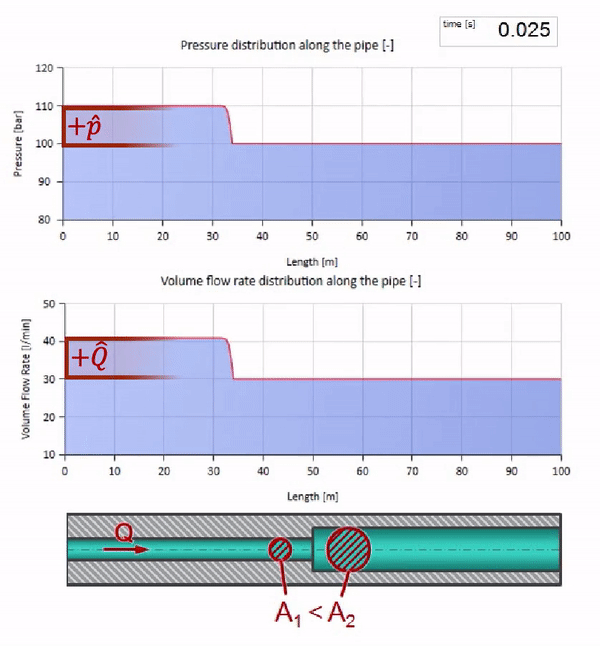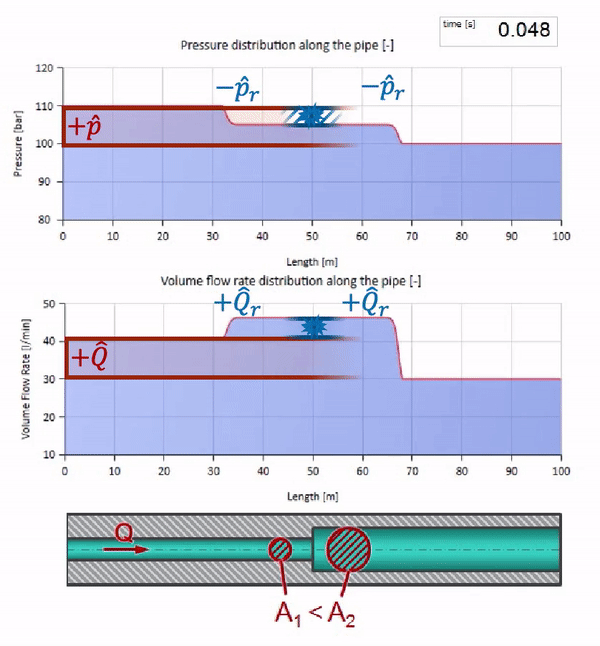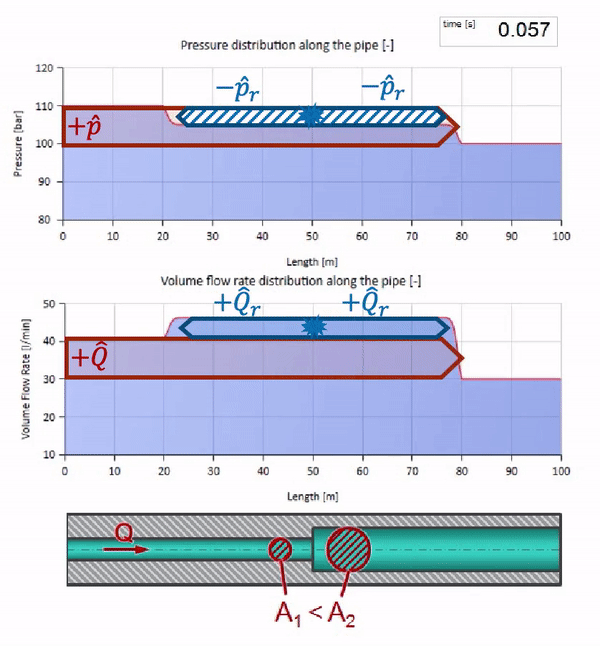
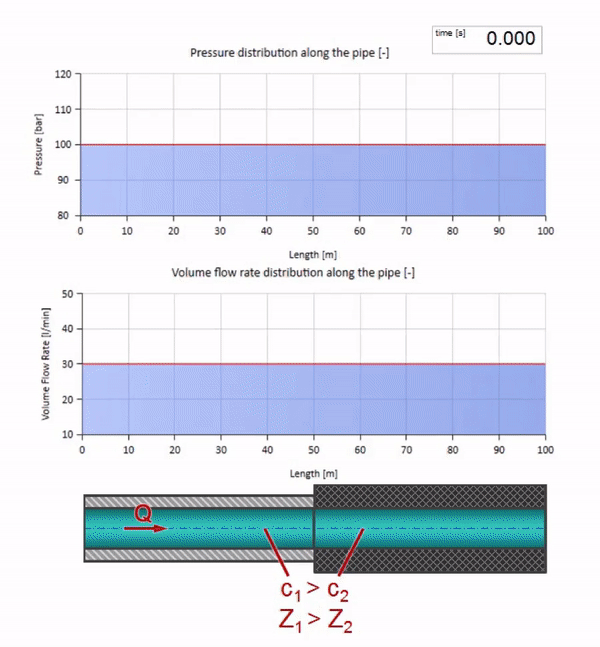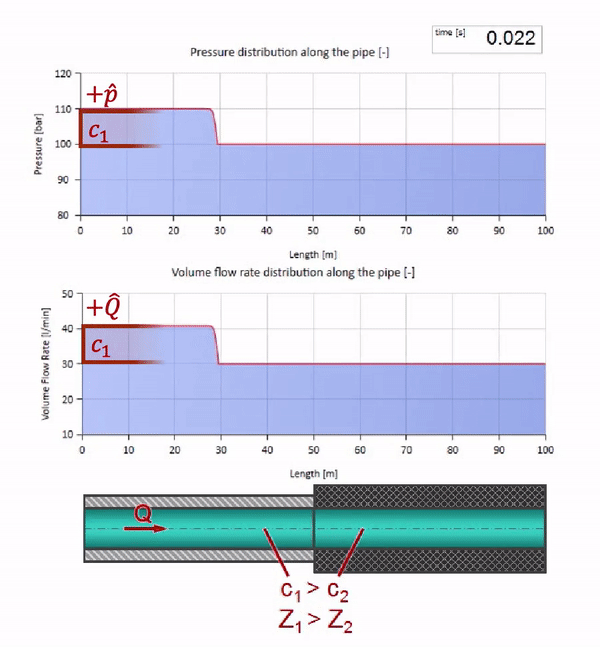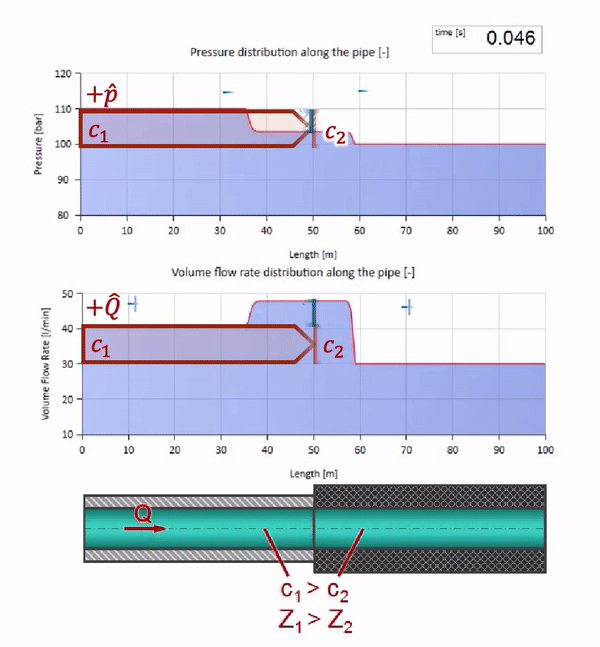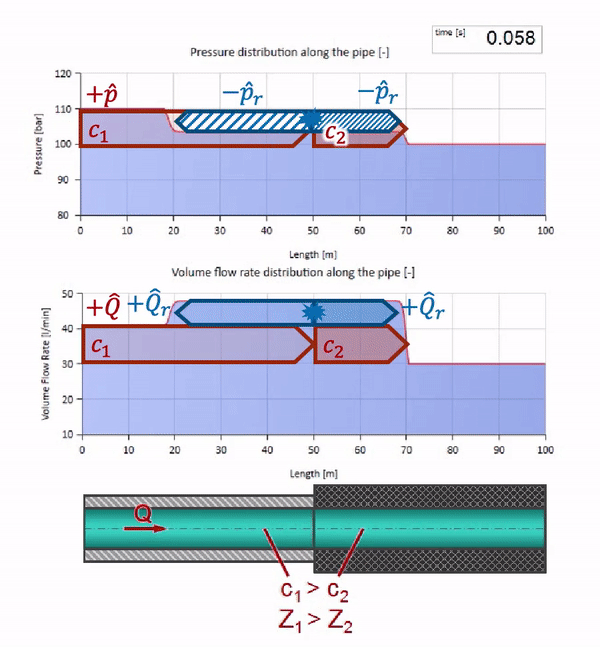
الآن نعلم أن كل أنبوب يحتوي على سائل له خاصية مثل مقاومة الموجة. من المثير للاهتمام أن نرى ما سيحدث للموجة إذا تغير قطر الأنبوب في قسم معين بشكل كبير:

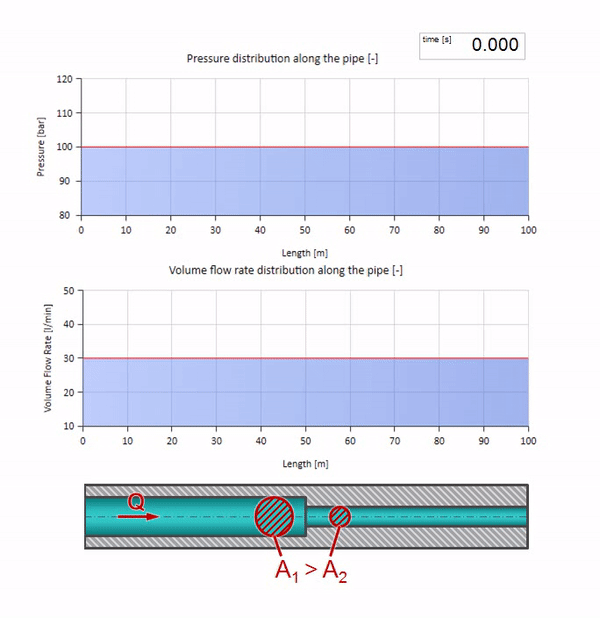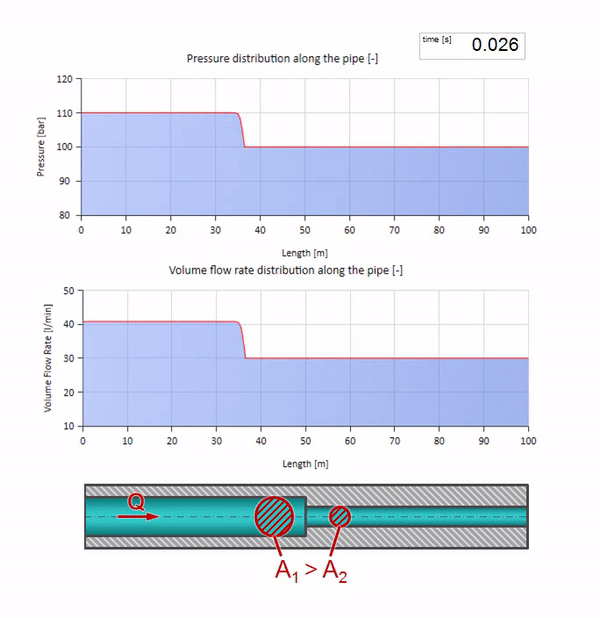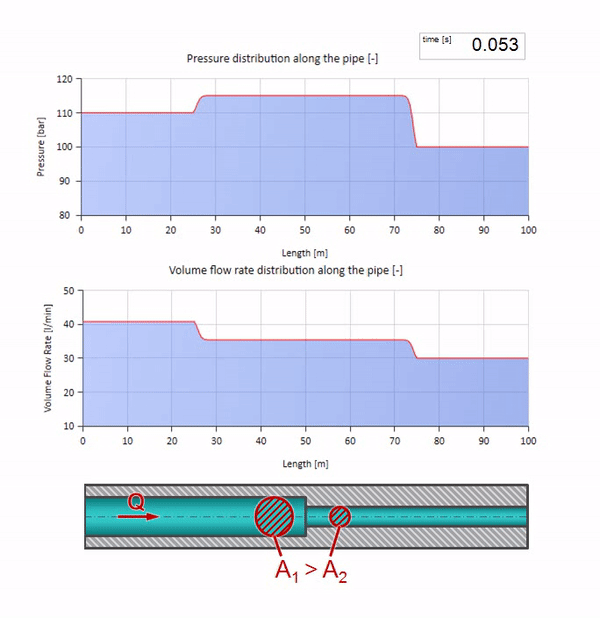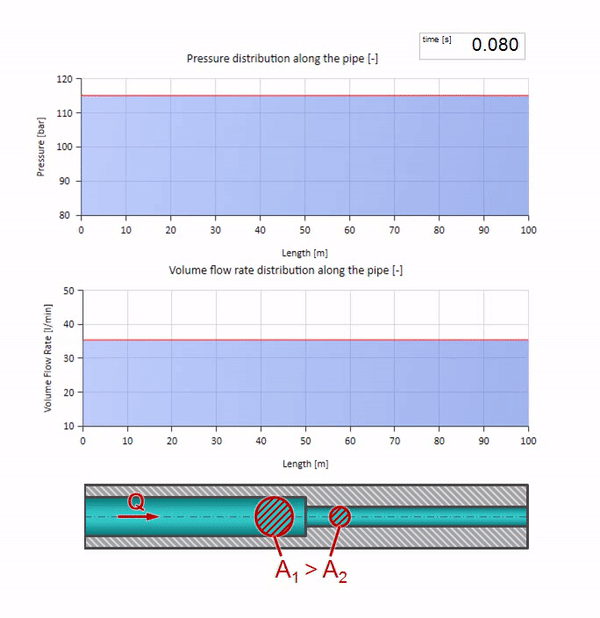
قبل أن تصل الموجة إلى مكان مع انخفاض في قطر الأنبوب ، بالطبع ، لا يحدث شيء مثير للاهتمام. ولكن بعد ذلك يصل إلى قسم بمقاومة أعلى للموجة ، مما يعني أن نسبة موجة الضغط إلى موجة التدفق يجب أن تكون أكبر مما كانت عليه في قسم الأنبوب الأيسر. وهذا يعني أن موجة الضغط يجب أن تزداد ، وأن ينخفض ​​معدل التدفق. في الوقت نفسه ، لم يتبق شيء للموجة باستثناء الانحناء إلى اليسار ، مع الحفاظ على قيم متساوية عند تقاطع الأنبوبين.

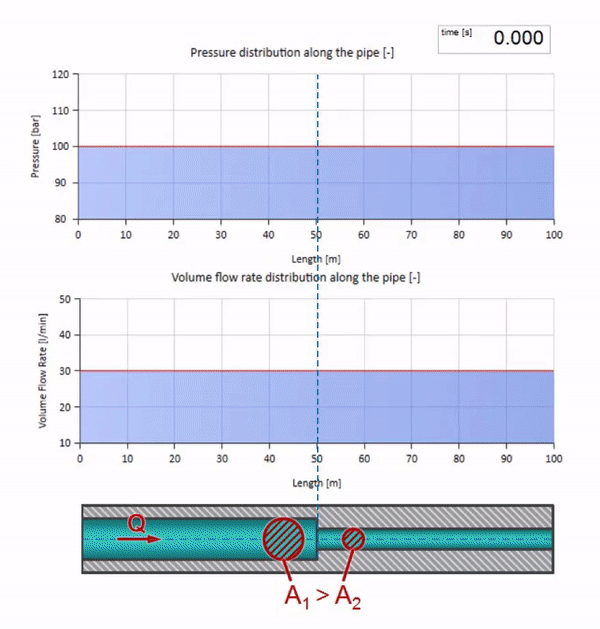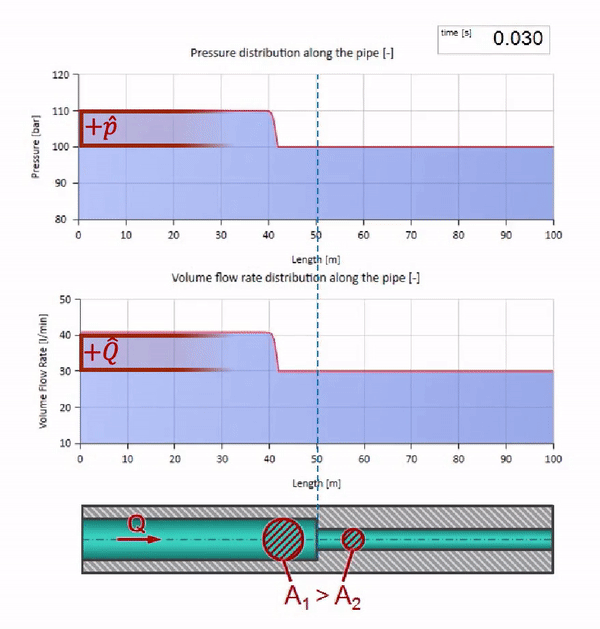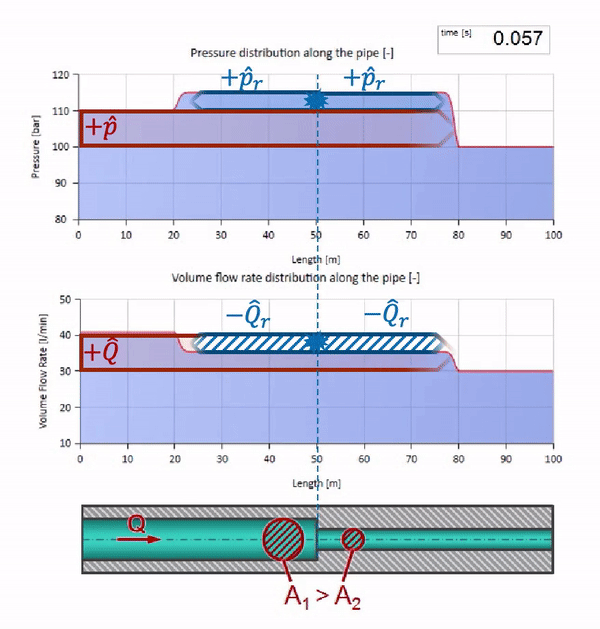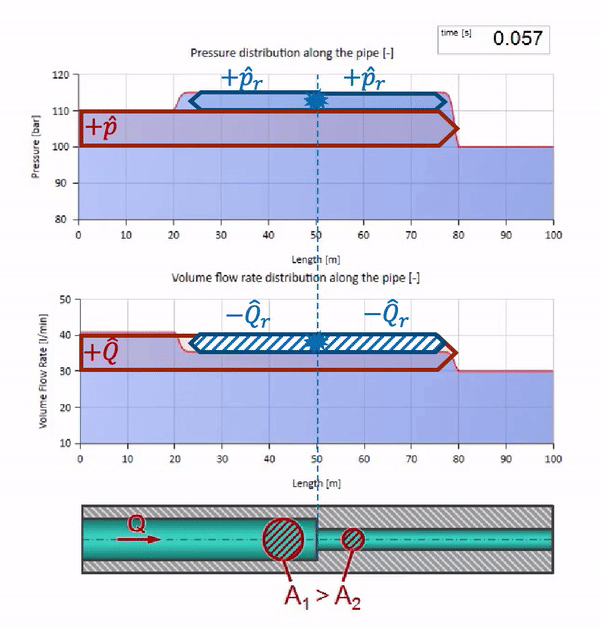
للحسابات ، من الملائم استخدام معامل الانعكاس $$$r$، والتي تعتبر من معاوقة الموجة للأقسام الفردية:

$$

$$r = \ frac {Z_2-Z_1} {Z_1 + Z_2}$$

ثم يمكن حساب الضغط المنعكس وموجات التدفق على النحو التالي:

$$

$${\ widehat p} _r = r \؛ \ widehat p$$

$$

$${\ widehat Q} _r = - \ frac {\ displaystyle \؛ {\ widehat p} _r} {Z_1} = - r \؛ \ widehat Q$$

وهذه الموجات نفسها سوف تكون متراكبة وفقًا لقانون التدخل مع الموجة الأصلية.
وستبدو كصورة انعكاس لموجة من موقع ذات مقاومة أقل للموجة:

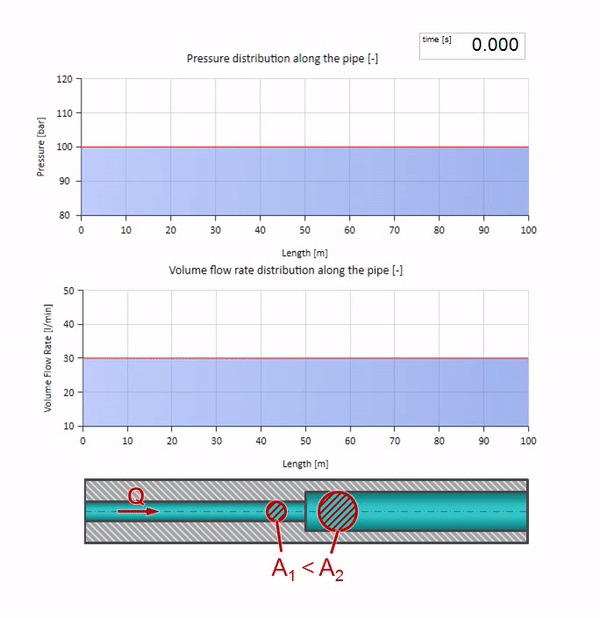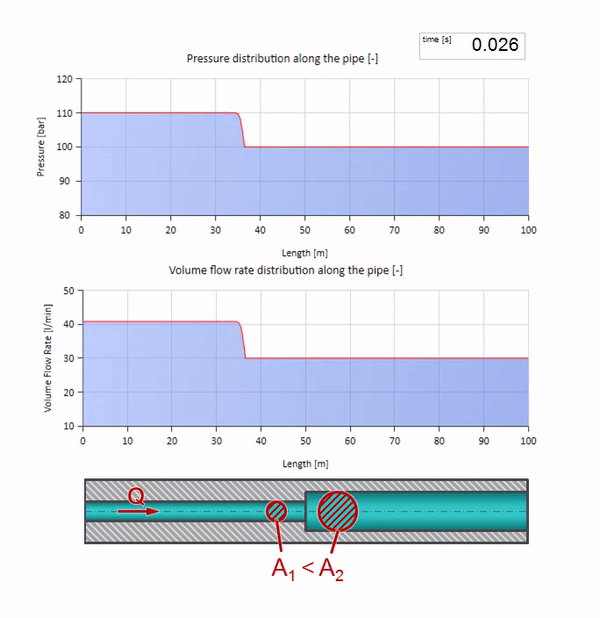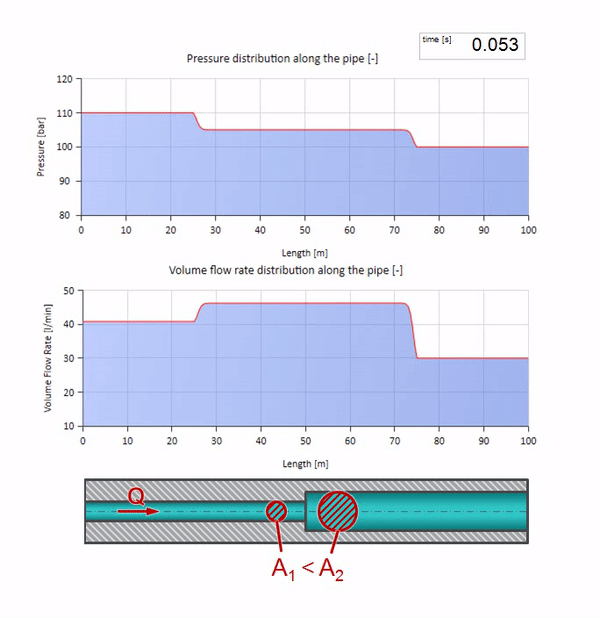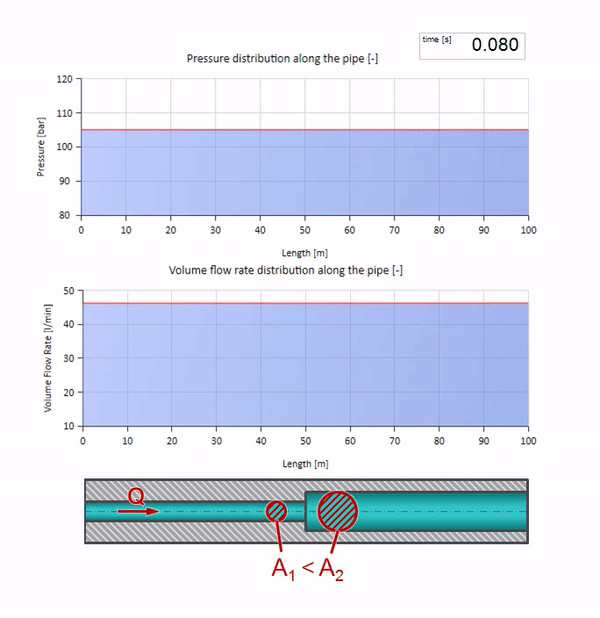
يمكن ملاحظة أن معامل الانعكاس هذه المرة سلبي ، مما يعني أن موجة الضغط بعد الانعكاس ستكون أقل ، ومعدل التدفق ، على العكس ، أكثر.

يجب أن نتذكر أن الممانعة لا تعتمد فقط على حجم الأنبوب ، ولكن أيضًا على سرعة الصوت المحلية. أي إذا كان لدينا قسم مواسير مع كم مطاطي تكون فيه سرعة الصوت أقل بكثير ، فستنعكس الموجة أيضًا:

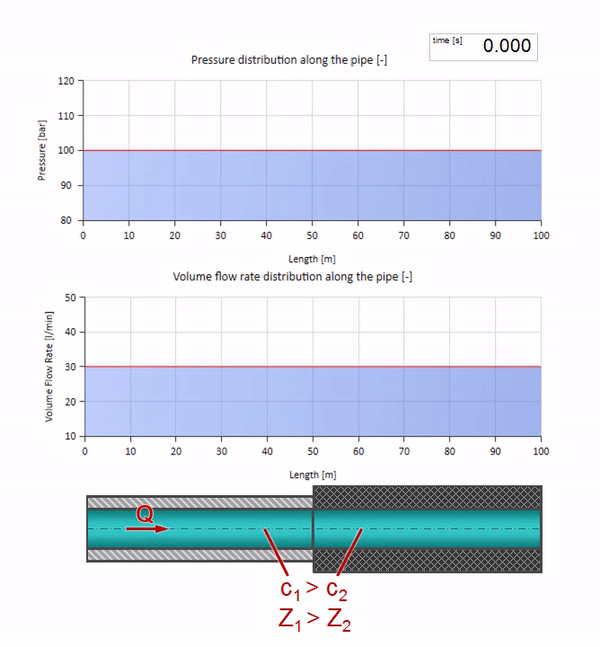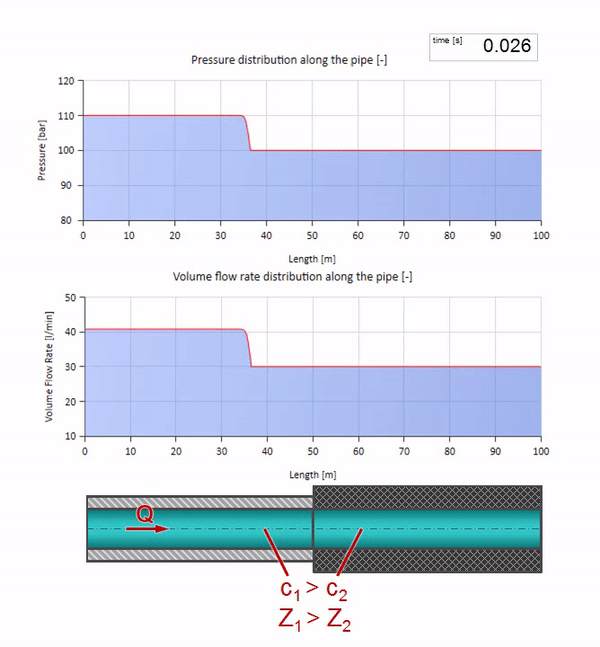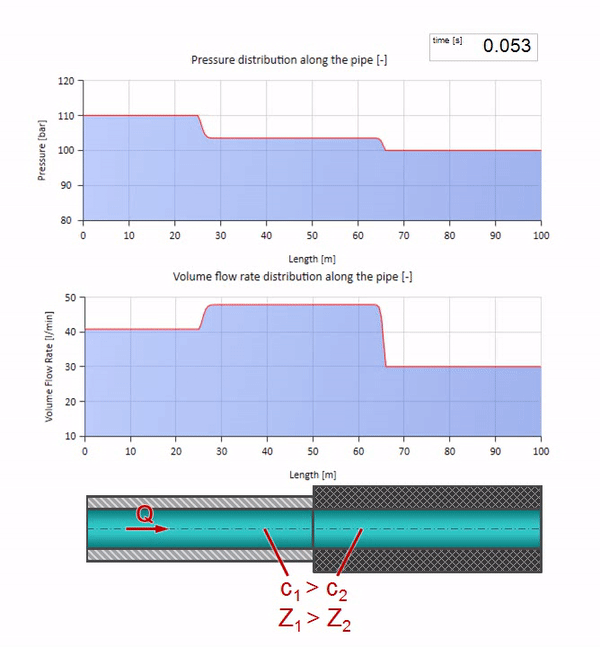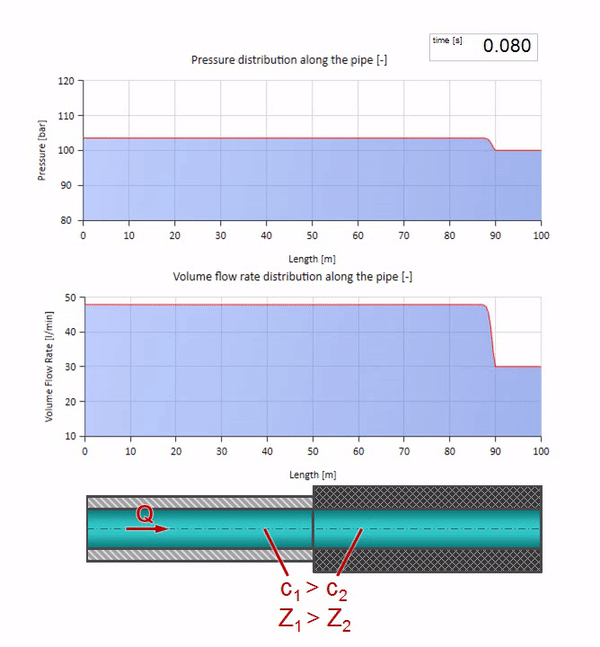
أولاً ، يجذب العين على الفور أن الموجة في القسم مع الجدار المطاطي للأنبوب تتحرك ببطء أكثر. وبما أن مقاومة الموجة أقل ، فإن نتيجة الانعكاس ستشبه الحالة مع تمدد الأنبوب:

سيكون من الجيد الآن أن نفكر في الحالات المتطرفة التي لا تحتوي على قيمة كبيرة ومقاومة كبيرة لمقاومة الموجه. سيكون هذا مخرج خط الأنابيب في الخزان بضغط مستمر ونهاية مغلقة ، على التوالي. سأترك هذه الرسوم المتحركة دون تعليق:


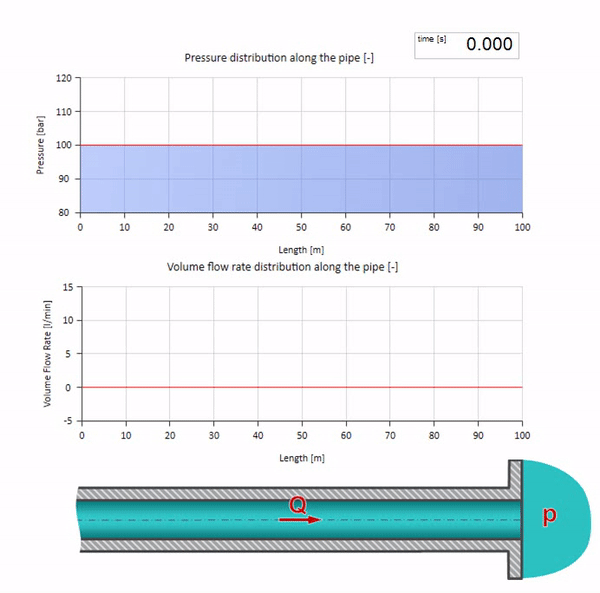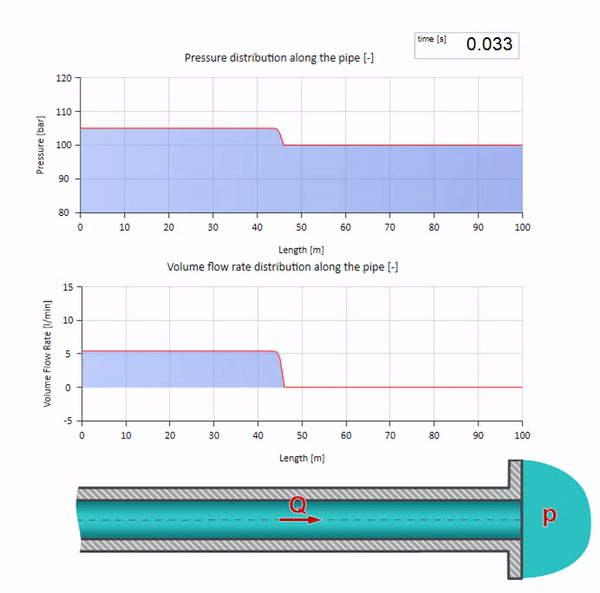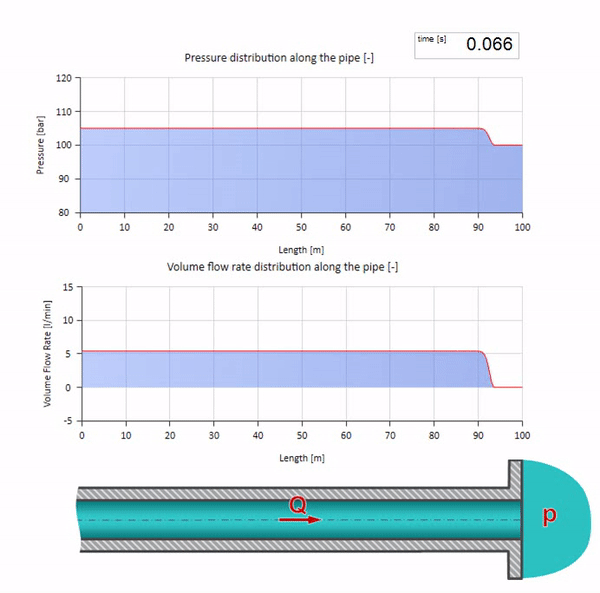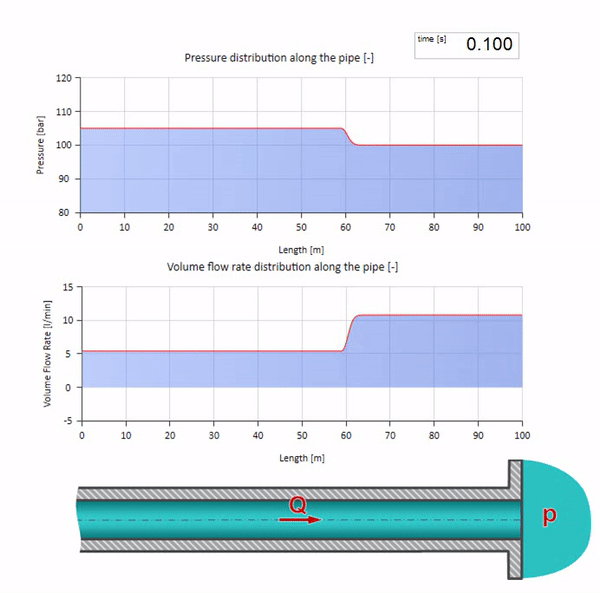
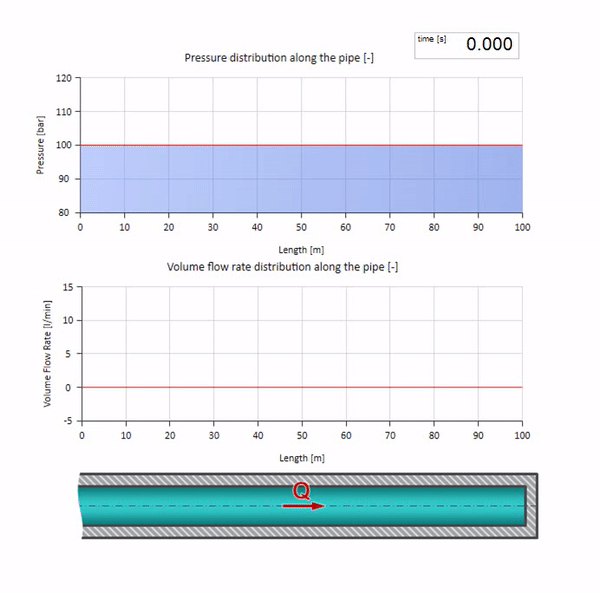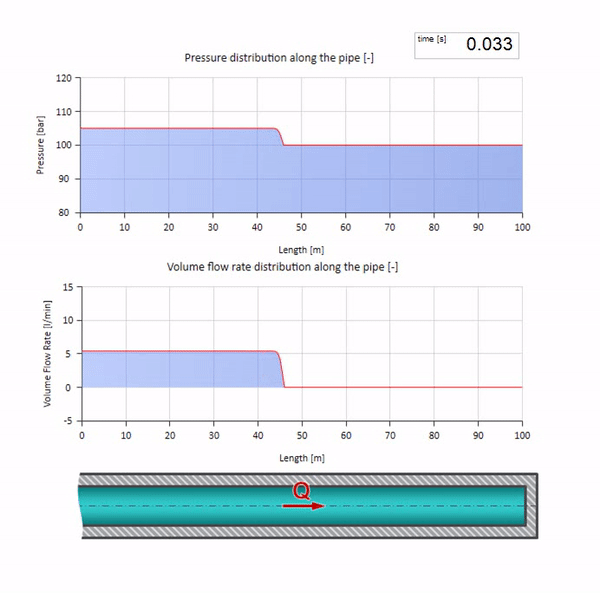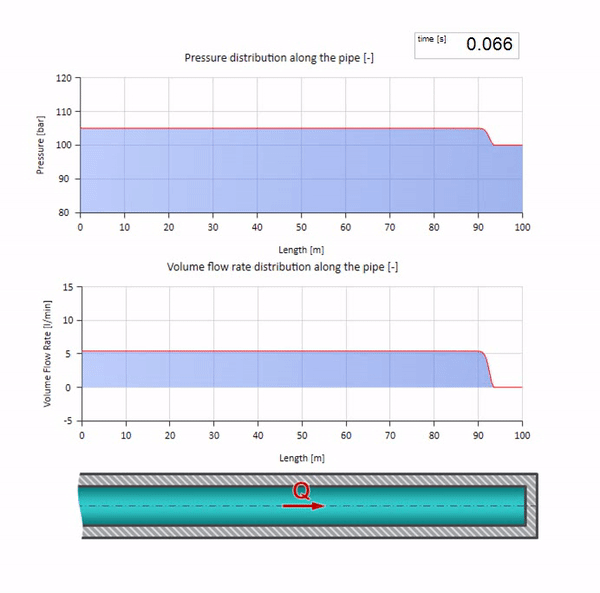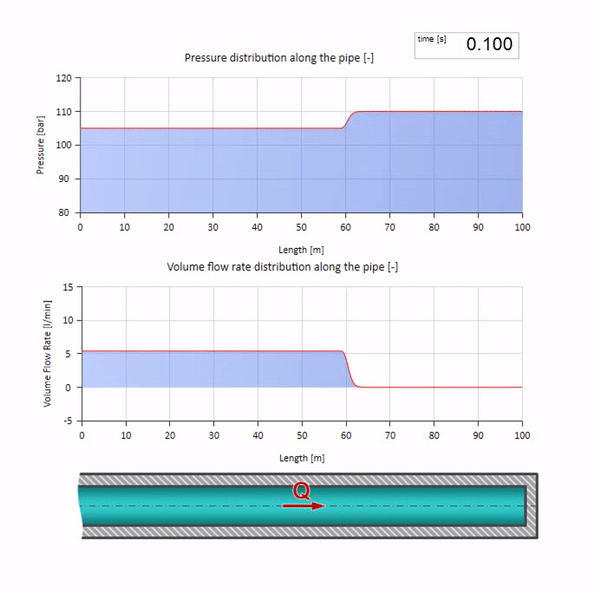
حسنًا ، إذا دمجنا هاتين الحالتين ، فإننا نحصل على صدمة هيدروليكية كلاسيكية:

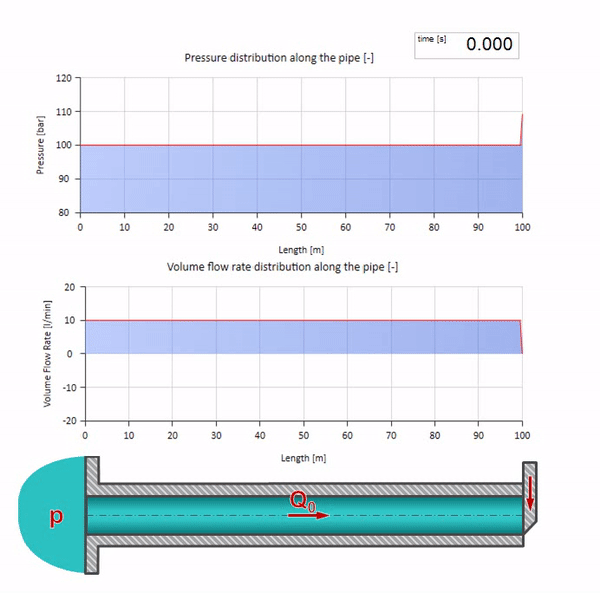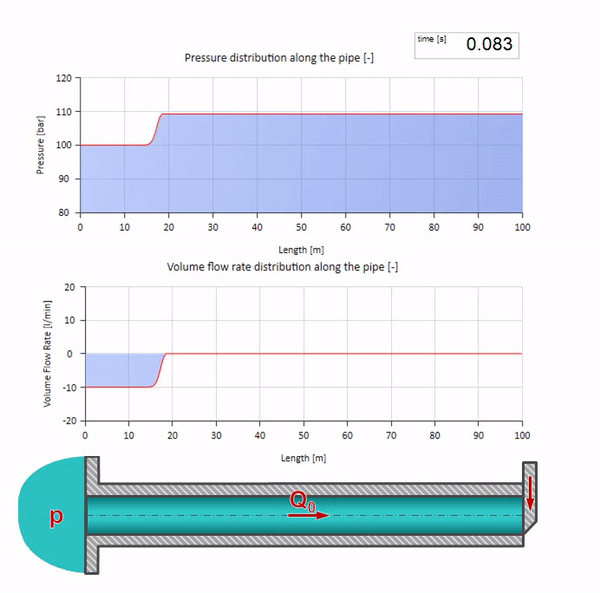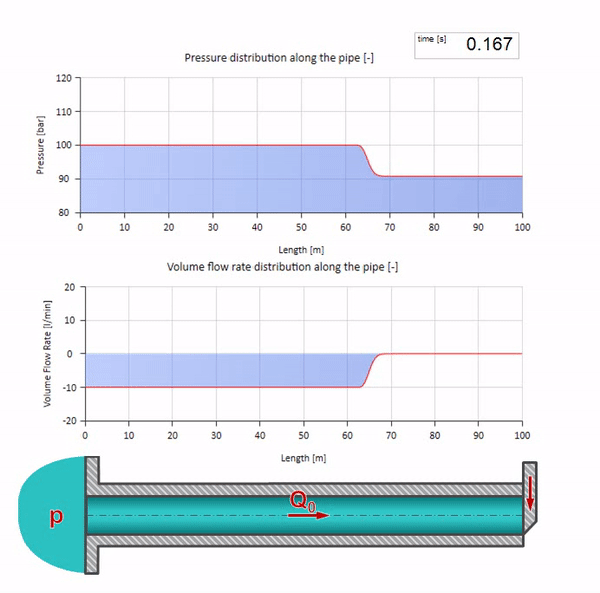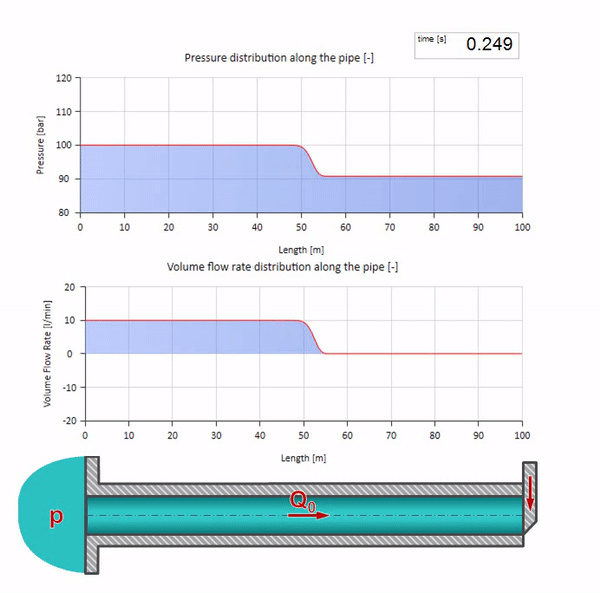
هنا ، في اللحظة الأولى من الوقت ، هناك بعض قيمة التدفق التي تساوي على الفور صفرًا في الطرف الأيمن من الأنبوب (يغلق الصمام). تبدأ موجة من السقوط المتدفق والضغط المتزايد بالتحرك إلى اليسار. تنعكس هذه الموجات من الطرف الأيمن لخط الأنابيب بدون مقاومة. في حالة عدم وجود احتكاك ، ستكون هذه العملية لا نهاية لها.
من المثير للاهتمام ، باستخدام الصيغ أعلاه ، يمكننا استخلاص معادلة جوكوفسكي لمطرقة المياه:

$$

$$\ widehat p = Z_L \ widehat Q \؛$$

نعبر عن معدل التدفق من خلال السرعة ، بافتراض أنه ينخفض ​​من قيمة معينة إلى الصفر ، ونرسم مقاومة الموجة:

$$

$$\ widehat p = A \؛ v_0 \؛ \ frac {\ rho \؛ c} {\ A} = \ rho \؛ c \؛ v_0$$

نحصل على قيمة قفزة الضغط التي تحدث عندما يتم إغلاق الغالق على الفور.

ملاحظات

1. لقد ألهمتني كتابة مقال كتبه رئيس كتاب أساسي عن علم الهيدروليكا في قسم الهندسة الهيدروليكية بجامعة الراين-ويستفاليان التقنية في آخن ، حيث أرى أن العمليات في الخطوط الهيدروليكية موصوفة بشكل أوضح (Grundlagen der Fluidtechnik Teil 1: Hydraulik ، Hubertus Murrenhoff ISBN: 978-3-8440 -1223-1).
2. تم عمل الرسوم المتحركة في برنامج SimulationX ، وقد تم الحساب بطريقة الخصائص