قرأت كتابًا موثوقًا به حول استراتيجيات التداول وكتبت روبوت التداول الخاص بي. لدهشتي ، لا يجلب الروبوت الملايين ، حتى التداول فعليًا. والسبب واضح: يحتاج الروبوت ، مثل سيارة السباق ، إلى "ضبط" ، لتحديد المعلمات التي تتكيف مع سوق معينة ، وفترة زمنية محددة.
نظرًا لأن الروبوت يحتوي على إعدادات كافية ، فإنه يتكرر على جميع مجموعاته المحتملة بحثًا عن أفضل مهمة تستغرق وقتًا طويلاً. في وقت ما ، أثناء حل مشكلة التحسين ، لم أجد اختيارًا معقولاً لخوارزمية البحث للمتجه شبه الأمثل لمعلمات روبوت التداول. لذلك ، قررت مقارنة عدة خوارزميات بشكل مستقل ...
بيان موجز لمشكلة التحسين
لدينا خوارزمية تداول. بيانات الإدخال - سجل أسعار الفاصل الزمني للساعة لمدة عام واحد من المراقبة. بيانات المخرجات - P - الربح أو الخسارة ، القيمة العددية.
تحتوي خوارزمية التداول على 4 معلمات قابلة للتكوين:
- وسط هو فترة المتوسط المتحرك "السريع" ،
- فترة السيدة من المتوسط المتحرك "البطيء"
- T - TakeProfit ، مستوى الربح المستهدف لكل معاملة فردية ،
- S - StopLoss ، مستوى الخسارة المستهدف لكل معاملة فردية.
نقوم بتعيين نطاق وخطوة تغيير ثابتة لكل معلمة ، بإجمالي
20 قيمة لكل معلمة.
وبالتالي ، يمكننا البحث عن الحد الأقصى للربح (P) لمعلمة واحدة على صفيف واحد من بيانات الإدخال:
- تختلف معلمة واحدة ، على سبيل المثال ، P = f (Ms) ، تنتج ما يصل إلى 20 اختبارًا خلفيًا ،
- تختلف معلمتين ، على سبيل المثال ، P = f (Ms ، T) ، تنتج ما يصل إلى 20 * 20 = 400 اختبار خلفي ،
- متغيرة ثلاث معلمات ، على سبيل المثال ، P = f (Mf ، Ms ، T) ، تنتج ما يصل إلى 20 * 20 * 20 = 8000 اختبار خلفي ،
- بتغيير كل من المعلمات ، P = f (Mf ، Ms ، T ، S) وإنتاج ما يصل إلى 20 ^ 4 = 160،000 اختبار خلفي.
ومع ذلك ، بالنسبة لمعظم خوارزميات التداول ، يستغرق الأمر عدة أوامر من الحجم لمزيد من الوقت لإجراء اختبار واحد. الأمر الذي يقودنا إلى مهمة العثور على ناقل شبه مثالي للمعلمات دون الحاجة إلى التكرار على مجموعة كاملة من التركيبات الممكنة.
تفاصيل حول التجارة والروبوتات التجاريةالتداول في البورصة ، الرهان في مركز تداول الفوركس ، الرهانات المجنونة على "الخيارات الثنائية" ، المضاربة بالعملات المشفرة - نوع من "التشخيص" ، مع العديد من الخيارات الممكنة لتطوير "المرض". سيناريو شائع جدًا عندما يأتي اللاعب ، بعد لعب "الحدس" ، إلى التداول التلقائي. لا تفهموني خطأ ، لا أريد أن أركز على هذا النحو بحيث تعارض الروبوتات التجارية الصارمة "من الناحية التكنولوجية والرياضية" التداول "اليدوي" الساذج والعديم. على سبيل المثال ، أنا مقتنع بأن أي من محاولاتي لجني الأرباح من سوق فعالة (اقرأ من أي سوق شفافة وسائلة) من خلال المضاربة ، سواء كانت تقديرية أو آلية بالكامل ، هي محكوم عليها بالفشل. إذا ، ربما ، لعدم السماح لعامل الحظ العشوائي.
ومع ذلك ، فإن التداول ، وبوجه خاص ، تجارة الحمية (الإيقاعية) ، هي هواية شائعة للكثيرين. بعض برامج الروبوت التجارية بشكل مستقل ، والبعض الآخر يذهب أبعد من ذلك ويخلق منصاتهم الخاصة للكتابة ، وتصحيح الأخطاء واستراتيجيات التداول مرة أخرى ، بينما يقوم البعض الآخر بتنزيل / شراء "خبير" إلكتروني جاهز. ولكن حتى أولئك الذين لا يكتبون خوارزميات التداول بأنفسهم ، يجب أن يكون لديهم فكرة عن كيفية التعامل مع هذا "الصندوق الأسود" للاستفادة منه وفقًا لفكرة المؤلف. لكي لا يكون لي أساس من الصحة ، أقدم ملاحظاتي الإضافية باستخدام مثال لاستراتيجية تداول بسيطة:
روبوت تداول بسيط
يحلل روبوت التداول ديناميات قيمة الذهب ، بالدولار لكل أونصة تروي ، ويقرر "شراء" أو "بيع" كمية معينة من الذهب. من أجل البساطة ، نفترض أن الروبوت يتداول دائمًا في أونصة واحدة.
على سبيل المثال ، في وقت الشراء ، كانت تكلفة أوقية الذهب من الذهب 1075.00
دولارًا أمريكيًا . في وقت البيع اللاحق (إغلاق المعاملة) ، ارتفع السعر إلى 1079.00 دولار أمريكي. بلغ الربح على هذه المعاملة 4 دولارات أمريكية.
إذا قام الروبوت "ببيع" الذهب بسعر 1075.00 دولارًا أمريكيًا ، وأكمل بعد ذلك (مغلقًا) المعاملة عن طريق "شراء" الذهب بسعر 1079 دولارًا أمريكيًا ، فسيكون الربح على المعاملة سلبًا - ناقص 4 دولارات أمريكية. في الواقع ، لا يهم بالنسبة لنا كيف يبيع الروبوت الذهب ، الذي لا يمتلكه ، من أجل "إعادة شرائه" لاحقًا. يسمح الوسيط / مركز التداول للمتداول "بشراء" و "بيع" أحد الأصول بطريقة أو بأخرى ، وكسب (أو ، في كثير من الأحيان ، الخسارة) ، على الفرق في الأسعار.
قررنا
بيانات الإدخال للروبوت - هذه ، في الواقع ، السلسلة الزمنية لأسعار (عروض الأسعار) للذهب. إذا قلت أن المثال الذي قدمته بسيط للغاية ، وليس حيويًا - يمكنني أن أؤكد لك: معظم الروبوتات التي يتم تداولها في السوق (وفي الواقع التجار أيضًا) في تداولهم يتم توجيههم فقط من خلال إحصائيات أسعار السلع التي يتداولونها. على أي حال ، في مشكلة التحسين البارامترية لإستراتيجية التداول ، لا يوجد فرق جوهري بين تداول الروبوت على أساس ناقل السعر والروبوت الذي يصل إلى مجموعة تيرابايت من تحليلات السوق متعددة الفرز. الشيء الرئيسي هو أنه يمكن (يجب أن يكون قادرًا) اختبار هذين الروبوتين على البيانات التاريخية. يجب تحديد الخوارزميات: أي أنه على نفس بيانات الإدخال (وقت النموذج ، إذا لزم الأمر ، يمكننا أيضًا أن نأخذها كمعلمة) ، يجب أن يظهر روبوت التداول نفس النتيجة.
يمكن العثور على مزيد من التفاصيل حول روبوت التداول في المفسد التالي:
خوارزمية تداول الروبوت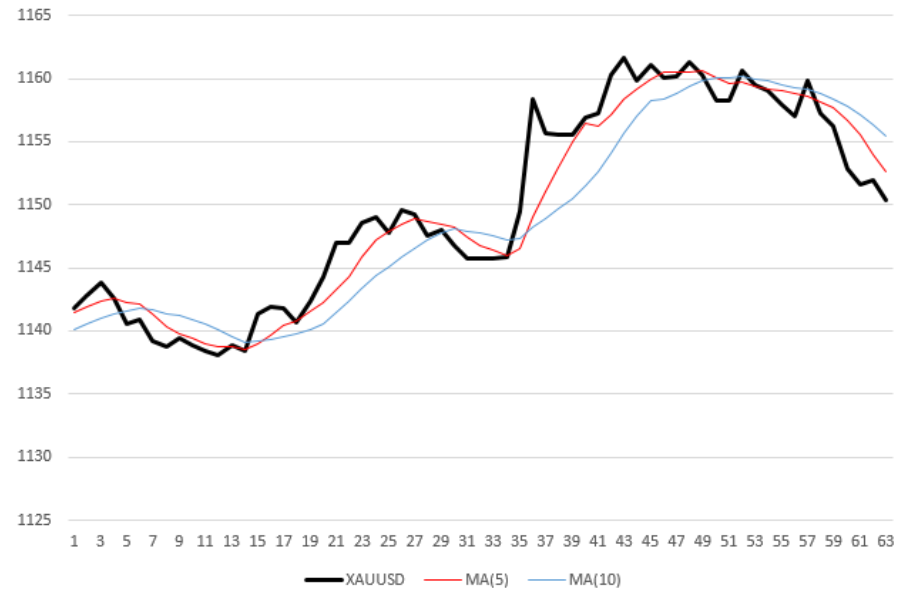
المنحنى الأسود (السميك) على الرسم البياني هو قياس سعر
XAUUSD لكل ساعة. خطان رقيقان مكسوران ، أحمر وأزرق - متوسط قيم السعر بمتوسط فترات 5 و 10 على التوالي. بمعنى آخر ، المتوسط المتحرك (MA) بفترات 5 ، 10. على سبيل المثال ، من أجل حساب إحداثيات النقطة الأخيرة (اليمنى) من المنحنى الأحمر ، أخذت متوسط القيم السعرية الخمس الأخيرة. وبالتالي ، فإن كل متوسط متحرك ليس "سلسًا" بالنسبة إلى منحنى السعر فحسب ، بل يتأخر أيضًا بمقدار نصف الفترة بالنسبة له.
قاعدة فتح المعاملات
يمتلك الروبوت قاعدة بسيطة لاتخاذ قرار الشراء / البيع:
- بمجرد أن يتجاوز المتوسط المتحرك مع فترة قصيرة (
MA "سريع") المتوسط المتحرك مع فترة طويلة (MA "بطيء") من الأسفل إلى الأعلى ، يشتري الروبوت أحد الأصول (الذهب).
بمجرد أن يتخطى MA "MA" المتوسط المتحرك "البطيء" من الأعلى إلى الأسفل ، يبيع الروبوت الأصل. في الشكل أعلاه ، سيقوم الروبوت بإجراء 5 معاملات: 3 مبيعات في طوابع زمنية 7 و 31 و 50 ومشترين (العلامات 16 و 36).
يسمح للروبوت بفتح عدد غير محدود من المعاملات. على سبيل المثال ، في مرحلة ما ، قد يكون لدى الروبوت العديد من عمليات الشراء والمبيعات المعلقة في نفس الوقت.
قاعدة إغلاق الصفقة
يقوم الروبوت بإغلاق الصفقة بمجرد:
- الربح على المعاملة يتجاوز العتبة المحددة في النسبة المئوية - TakeProfit ،
- أو الخسارة في المعاملة ، في المئة ، تتجاوز القيمة المقابلة - StopLoss.
افترض أن StopLoss هو 0.2٪.
الصفقة هي "بيع" للذهب بسعر 1061.50.
بمجرد أن يرتفع سعر الذهب إلى 1061.50 + 1061.50 * 0.2٪ / 100٪ = 1063.12٪ ، من الواضح أن خسارة الصفقة ستكون 0.2٪ وسيغلق الروبوت الصفقة تلقائيًا.
يتخذ الروبوت جميع القرارات المتعلقة بفتح / إغلاق الصفقة في نقاط منفصلة في الوقت المناسب - في نهاية كل ساعة ، بعد نشر عرض أسعار XAUUSD التالي.
نعم ، الروبوت بسيط للغاية. في الوقت نفسه ، تلبي 100 ٪ متطلباتها:
- الخوارزمية حتمية: في كل مرة ، بمحاكاة عمل الروبوت على نفس بيانات الأسعار ، سنحصل على نفس النتيجة ،
- لديها عدد كاف من المعلمات القابلة للتعديل ، وهي: فترة "سريع" وفترة المتوسط المتحرك "البطيء" (الأرقام الطبيعية) و TakeProfit و StopLoss - أرقام حقيقية موجبة ،
- تغيير في كل من المعلمات الأربعة ، في الحالة العامة ، له تأثير غير خطي على خصائص التداول للروبوت ، على وجه الخصوص ، على ربحيته ،
- تعتبر ربحية الروبوت في تاريخ السعر رمزًا للبرنامج الأولي ، وتستغرق العملية الحسابية نفسها جزءًا من الثانية لمتجه الآلاف من عروض الأسعار ،
- أخيرًا ، والذي ، مع ذلك ، غير ذي صلة ، فإن الروبوت ، بكل بساطته ، في الواقع سيثبت أنه ليس أسوأ (وإن كان ربما ليس أفضل) من الكأس التي باعها المؤلف على الإنترنت مقابل مبلغ غير محتمل.
بحث سريع عن مجموعة شبه مثالية من معلمات الإدخال
باستخدام مثال روبوتنا البسيط ، يمكن ملاحظة أن التعداد الكامل لجميع المتجهات المحتملة لإعدادات الروبوت مكلف للغاية حتى بالنسبة لـ 4 معلمات متغيرة. بديل واضح للبحث الشامل هو اختيار ناقلات المعلمات لإستراتيجية محددة. نعتبر جزءًا فقط من جميع المجموعات الممكنة بحثًا عن أفضل مجموعة ، حيث يقترب
CF من الأعلى (أو الأصغر ، اعتمادًا على CF الذي نختاره والنتيجة التي نحققها).
سننظر في ثلاث خوارزميات بحث للقيمة شبه
المثالية للمرشح الرقمي . لكل خوارزمية ، قمنا بتعيين حد 40 اختبارًا (من 400 مجموعة ممكنة).
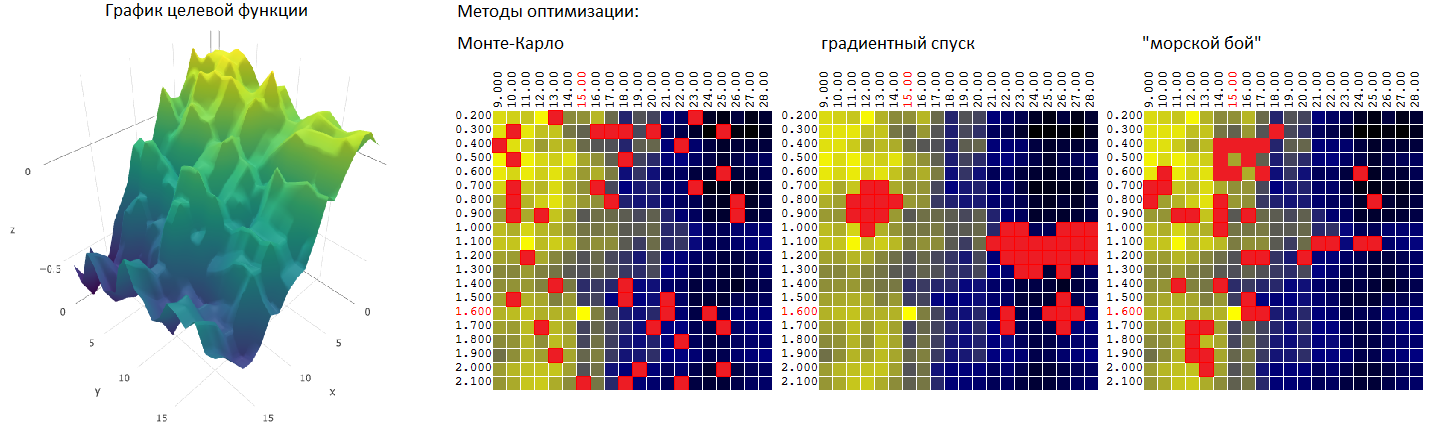
طريقة مونتي كارلو
أو اختيار عشوائي لناقلات M غير المترابطة من بين عدد ممكن من المجموعات يساوي N. ربما تكون الطريقة هي أبسط طريقة ممكنة. سوف نستخدمها كنقطة بداية للمقارنة اللاحقة مع طرق التحسين الأخرى.
مثال 1
يوضح الرسم البياني اعتماد الربح (P) لتداول روبوت التداول الخاص بنا
EURUSD ، الذي تم الحصول عليه على الجزء السنوي من تاريخ قياسات سعر الساعة ، على قيمة المعلمة - فترة
المتوسط المتحرك "البطيء" (M). جميع المعلمات الأخرى ثابتة وغير محسنة.
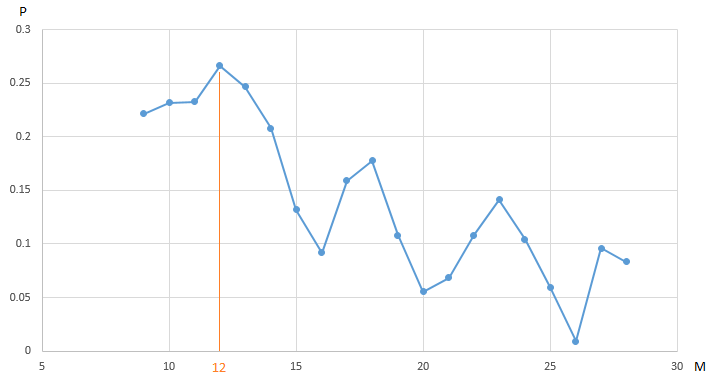
يصل CF (الربح) إلى 0.27 كحد أقصى عند النقطة M = 12. من أجل ضمان أقصى قيمة للربح ، نحتاج إلى إجراء 20 تكرارًا من الاختبار. والبديل هو إجراء عدد أقل من الاختبارات لروبوت التداول بقيمة محددة عشوائيًا للمعلمة M على الفاصل الزمني [9 ، 20]. على سبيل المثال ، بعد 5 تكرارات (20٪ من إجمالي عدد الاختبارات ، وجدنا متجهًا شبه مثالي (متجه ، من الواضح أنه أحادي البعد) من المعلمات: M = 18 بقيمة CF (M) تساوي 0.18:

تم إخفاء القيم المتبقية على الرسم البياني من خوارزمية التحسين بواسطة "ضباب الحرب".
لا يسمح لنا تحسين إحدى المعلمات الأربع لروبوت التداول الخاص بنا ، مع القيم الثابتة للمعلمات المتبقية ، برؤية الصورة الكاملة. ربما ليس الحد الأقصى 0.27 CF ليس أفضل قيمة للمؤشر ، إذا قمت بتغيير قيمة المعلمات الأخرى؟

هذه هي الطريقة التي يتغير بها اعتماد الربح على متوسط الفترة المتحركة لقيم مختلفة لمعلمة TakeProfit على الفاصل الزمني [0.2 ... 0.8].
طريقة مونت كارلو: تحسين معلمتين
يمكن وصف اعتماد ربح روبوت التداول على معلمتين بيانياً كسطح:

المحورين هما قيم المعلمات T (TakeProfit) و M (فترة المتوسط المتحرك) ، المحور الثالث هو قيمة الربح.
بالنسبة إلى روبوت التداول الخاص بنا ، بعد إجراء 400 اختبار على فترة بيانات لمدة عام واحد (~ 6000 اقتباسات للساعة باليورو مقابل الدولار الأمريكي) ، نحصل على سطح النموذج:

أو على المستوى حيث تمثل قيم الأصول المالية (الربح ، P) باللون:

اختيار النقاط العشوائية على متن الطائرة ، في هذا المثال ، لم تعثر الخوارزمية على القيمة المثلى ، لكنها اقتربت جدًا منها:

ما مدى فعالية طريقة مونت كارلو في العثور على الحد الأقصى
للتليف الكيسي ؟ بعد إجراء 1000 تكرار للبحث عن الحد الأقصى من CF على بيانات المصدر من المثال أعلاه ، حصلت على الإحصائيات التالية:
- بلغ متوسط قيمة الحد الأقصى لـ DF الموجود خلال 1000 تكرار تحسين (40 متجهًا عشوائيًا للمعلمات [M ، T] من أصل 400 توليفة ممكنة) 0.231 أو 95.7 ٪ من الحد الأقصى العالمي لـ DF (0.279).
من الواضح أنه عند مقارنة طرق التحسين البارامترية للروبوتات التجارية ، فإن عينة واحدة ليست مؤشرًا. ولكن في الوقت الحالي ، يكفي هذا التقييم. ننتقل إلى الطريقة التالية - طريقة
نزول التدرج .
طريقة هبوط التدرج
بشكل رسمي ، كما يوحي الاسم ، يتم استخدام الطريقة للبحث عن الحد الأدنى من DF.
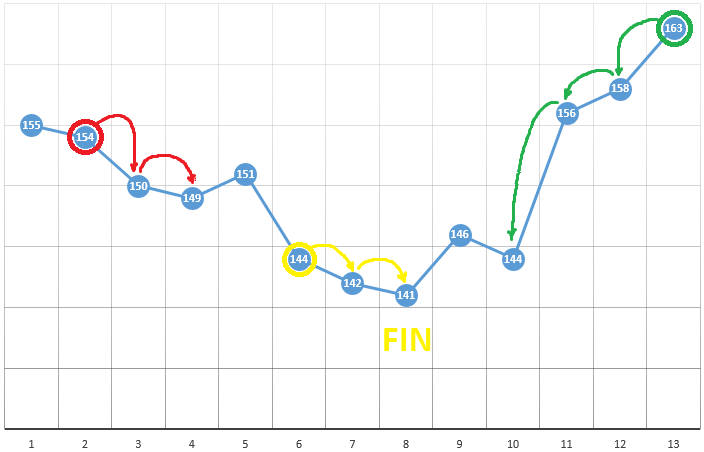
وفقًا للطريقة ، نختار نقطة البداية بالإحداثيات [x0 ، y0 ، z0 ، ...]. على مثال تحسين معلمة واحدة ، يمكن أن تكون هذه نقطة مختارة عشوائيًا:
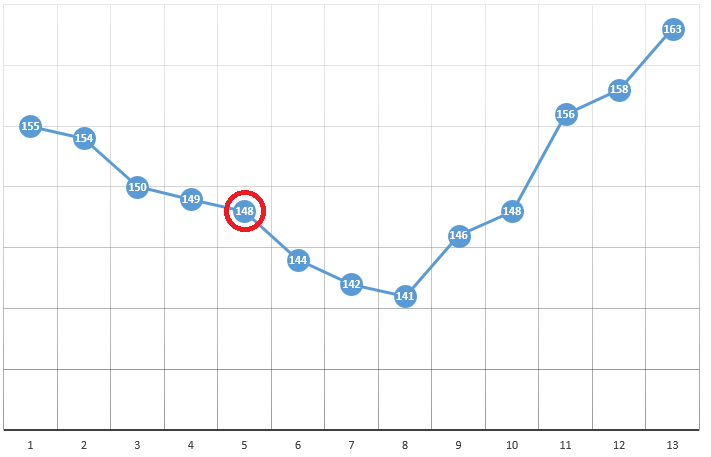
بإحداثيات [5] وقيمة DF بقيمة 148. فيما يلي ثلاث خطوات بسيطة:
- تحقق من قيم CF بالقرب من الموقع الحالي (149 و 144)
- انتقل إلى النقطة مع أصغر قيمة CF
- إذا كان هذا غائبًا ، تم العثور على أقصى محلي ، اكتملت الخوارزمية

لتحسين DF كدالة لمعلمتين ، نستخدم نفس الخوارزمية. إذا قمنا في وقت سابق بحساب CF في نقطتين متجاورتين
[xi−1]،[xi+1] ، نتحقق الآن من 4 نقاط:
[xi−1،yi]،[xi+1،yi]،[xi،yi−1]،[xi،yi+1].
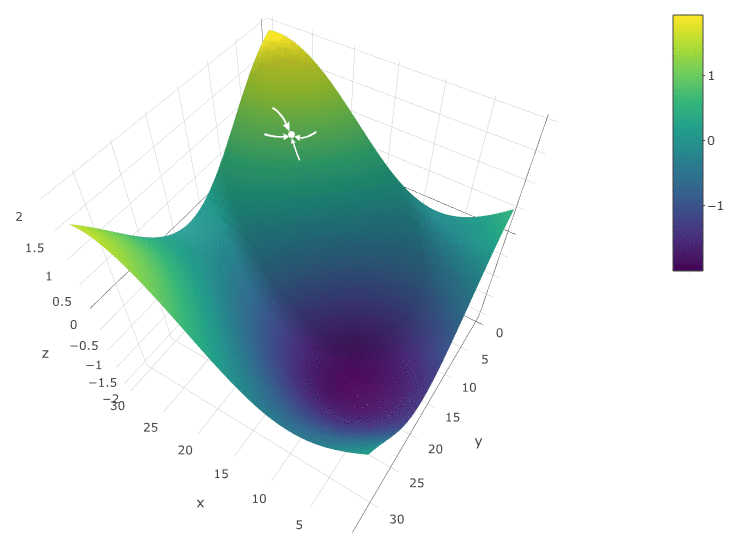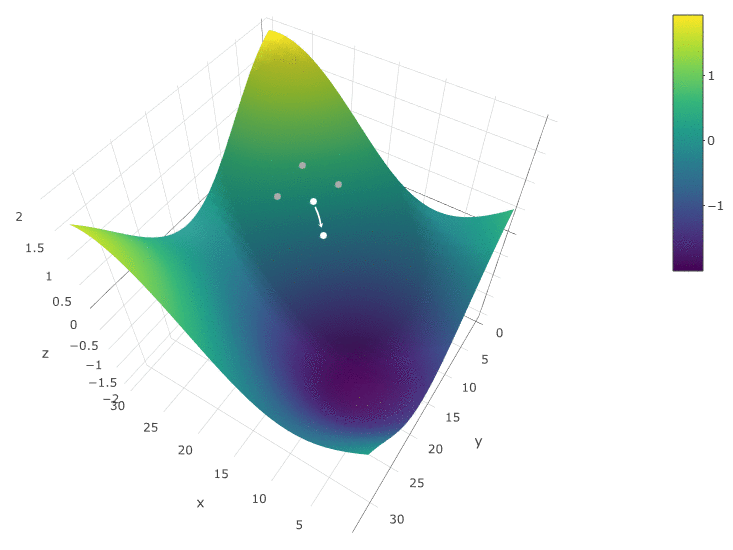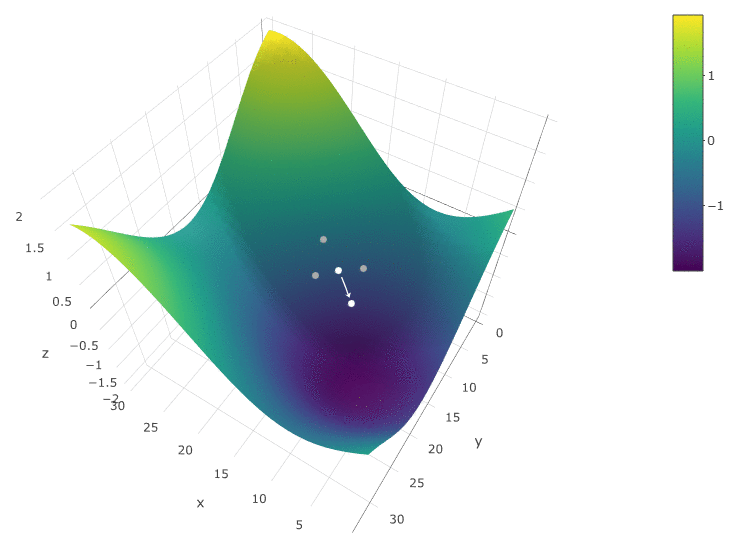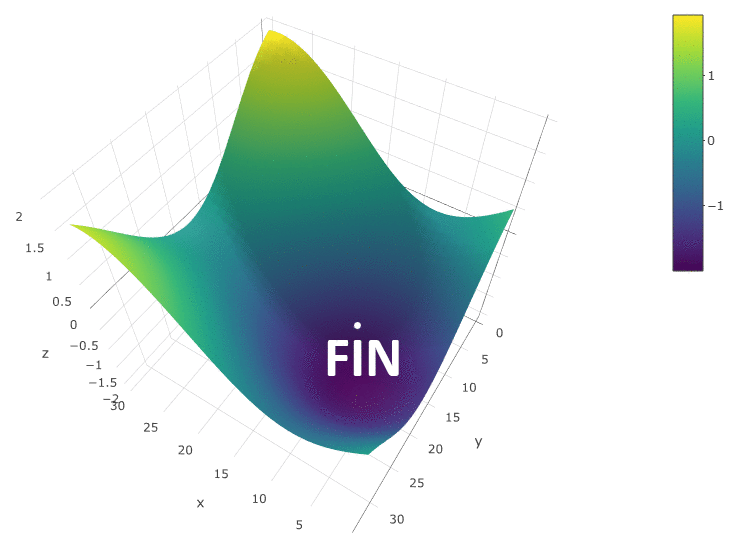
هذه الطريقة جيدة بالتأكيد عندما يكون هناك طرف واحد فقط في DF في مساحة الاختبار. إذا كان هناك العديد من الحالات القصوى ، فيجب تكرار البحث عدة مرات لزيادة احتمالية العثور على الحد الأقصى العالمي:
في مثالنا ، نحن نبحث عن
أقصى DF. للبقاء ضمن تعريف الخوارزمية ، يمكننا أن نفترض أننا نبحث عن الحد الأدنى "ناقص DF". كل نفس المثال ، ربح روبوت التداول كدالة لفترة المتوسط المتحرك وقيمة TakeProfit ، تكرار واحد:
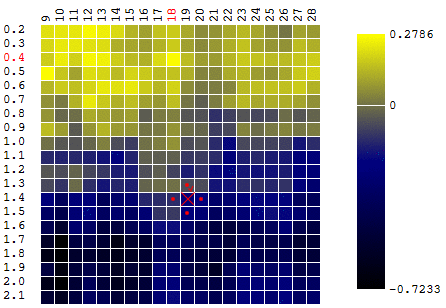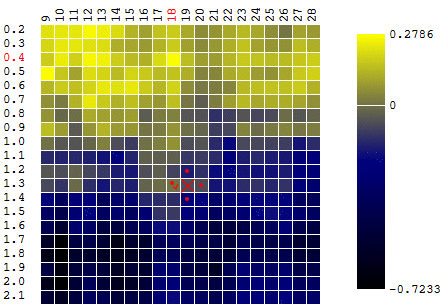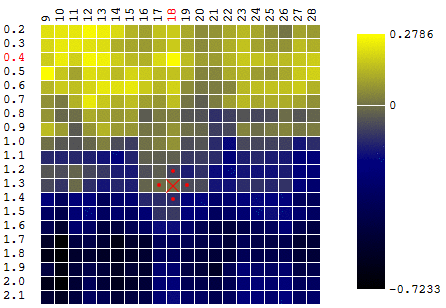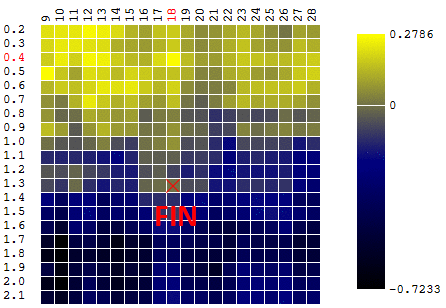
في هذه الحالة ، تم العثور على أقصى محلي بعيد عن الحد الأقصى العالمي للتليف الكيسي. مثال على عدة تكرارات للبحث عن أقصى FS من خلال طريقة نزول التدرج ، يتم حساب قيمة FS 40 مرة (40 نقطة من 400 ممكن):

الآن ، نقارن كفاءة البحث عن الحد الأقصى العالمي لل CF (الربح) في بياناتنا الأولية باستخدام مونتي كارلو وخوارزميات نزول التدرج. في كل حالة ، يتم إجراء 40 اختبارًا (حسابات CF). تم إجراء 1000 تكرار التحسين من خلال كل من الطرق:
| مونتي كارلو | أصل متدرج |
|---|
| متوسط القيمة شبه المثلى للتليف الكيسي | 0.231 | 0.200 |
| القيمة التي تم الحصول عليها من أقصى CF | 95.7٪ | 92.1٪ |
كما ترى من الجدول ، في هذا المثال ، فإن طريقة هبوط التدرج تؤدي بشكل أسوأ لمهمتها - للبحث عن الحد الأقصى العالمي للأصل الرقمي - أقصى ربح. لكننا لسنا في عجلة من أمرنا لتجاهلها.
الثبات المعياري لخوارزمية التداول
غالبًا ما لا يكون العثور على إحداثيات الحد الأقصى / الأدنى العالمي للفلتر الرقمي هدفًا للتحسين. لنفترض ، على الرسم البياني ، وجود ذروة "حادة" - الحد الأقصى العالمي ، وقيمة CF في محيطها أقل بكثير من قيمة الذروة:
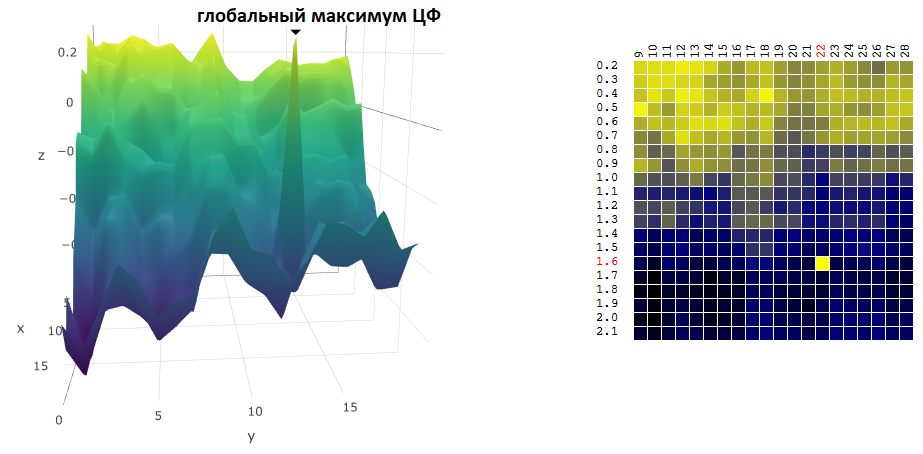
لنفترض أننا اخترنا إعدادات روبوت التداول الذي يتوافق مع الحد الأقصى الموجود للأصل الرقمي. إذا قمنا بتغيير قيمة واحدة على الأقل من المعلمات - فترة المتوسط المتحرك و / أو TakeProfit - ستنخفض ربحية الروبوت بشكل حاد (تصبح سلبية). فيما يتعلق بالتداول الحقيقي ، يمكن للمرء أن يتوقع على الأقل أن السوق الذي سيتداول فيه روبوتنا سيكون مختلفًا بشكل ملحوظ عن فترة التاريخ التي قمنا فيها بتحسين خوارزمية التداول.
لذلك ، عند اختيار الإعدادات "المثلى" لروبوت التداول ، يجدر الحصول على فكرة عن مدى حساسية الروبوت للتغيرات في الإعدادات بالقرب من أقصى نقطة تم العثور عليها في DF.
من الواضح أن طريقة الهبوط التدريجي ، كقاعدة ، تعطينا قيم TF في محيط الطرف الأقصى. من المرجح أن تصل طريقة مونتي كارلو إلى الساحات.
في تعليمات متعددة لاختبار استراتيجيات التداول الآلي ، بعد اكتمال التحسين ، يوصى بالتحقق من المؤشرات المستهدفة للروبوت في المنطقة المجاورة لمتجه المعلمة الموجود. لكن هذه اختبارات إضافية. بالإضافة إلى ذلك ، ماذا لو انخفضت ربحية الإستراتيجية مع تغيير طفيف في الإعدادات؟ من الواضح أن عليك تكرار عملية الاختبار.
ستكون الخوارزمية مفيدة لنا ، والتي ، في نفس الوقت الذي تبحث فيه عن أقصى حدود CF ، ستسمح لنا بتقييم استقرار استراتيجية التداول لتغيير الإعدادات في نطاق ضيق فيما يتعلق بالقمم التي تم العثور عليها. على سبيل المثال ، لا تبحث مباشرة عن الحد الأقصى للتليف الكيسي
P=f(mi،ti)،
وقيمة المتوسط المرجح التي تأخذ في الاعتبار القيم المجاورة للدالة الهدف ، حيث يتناسب الوزن عكسًا مع المسافة إلى القيمة المجاورة (لتحسين معلمتين x ، y والدالة الهدف P):
P′(xi،yi)= fracwi timesP(xi،yi)+wj timesP(xj،yj)+wk timesP(xk،yk)+...wi+wj+wk+...
wj= sqrt(xj−xi)2+(yj−yi)2
wi+wj+wk+...=1
بعبارة أخرى ، عند اختيار متجه شبه مثالي للمعلمات ، ستقيِّم الخوارزمية دالة الهدف "المتجانسة":
كان أصبح
أصبح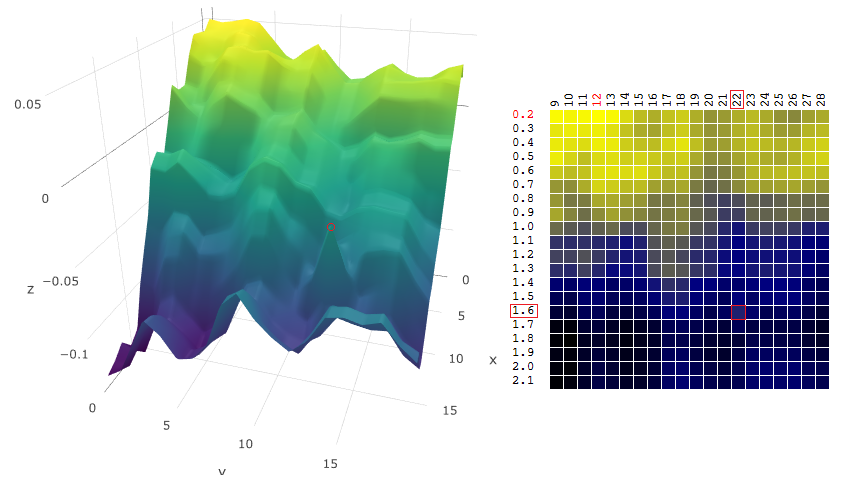
طريقة "معركة البحر"
في محاولة لدمج مزايا كلتا الطريقتين (مونتي كارلو وطريقة نزول التدرج) ، جربت خوارزمية مشابهة لخوارزمية اللعبة في "المعركة البحرية":
- أولاً ، أضرب بضع "ضربات" على المنطقة بأكملها
- ثم ، في أماكن "الضربات" ، أفتح نيرانًا هائلة.
وبعبارة أخرى ، يتم إجراء اختبارات N الأولى على نواقل عشوائية غير مرتبطة بمعلمات الإدخال. يتم اختيار أفضل النتائج من بين هذه. على مقربة من هذه الاختبارات (بالإضافة إلى - دقائق 0..L لكل من الإحداثيات) يتم إجراء اختبارات K أخرى.
بالنسبة لمثالنا (400 نقطة ، إجمالي 40 تجربة) لدينا:
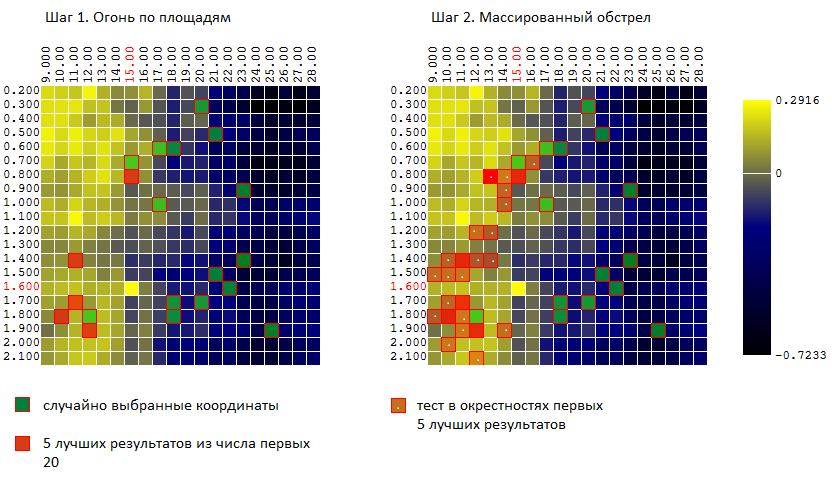
ومرة أخرى ، نقارن فعالية خوارزميات التحسين 3 الآن:
| مونتي كارلو | أصل متدرج | "معركة بحرية" |
|---|
متوسط قيمة الطرف الأقصى من CF كنسبة مئوية من القيمة العالمية.
40 اختبارًا ، 1000 تكرار تحسين
| 95.7٪ | 92.1٪ | 97.0٪ |
والنتيجة مشجعة. بالطبع ، تم إجراء المقارنة على عينة بيانات واحدة محددة: خوارزمية تداول واحدة في سلسلة زمنية واحدة لقيمة اليورو مقابل الدولار الأمريكي.
ولكن ، قبل مقارنة الخوارزميات على عدد أكبر من عينات بيانات المصدر ، سأتحدث عن خوارزمية أخرى غير متوقعة (غير مبررة؟) لتحسين استراتيجيات التداول - تحسين الخوارزمية الجينية (GA). ومع ذلك ، خرج المقال ضخمًا جدًا ، وسيتعين تأجيل الجمعية العامة إلى المنشور التالي .