هناك عدد من المهام التي تنقسم فيها الإشارة الطويلة إلى أجزاء ، تتم معالجة كل منها بشكل منفصل. على وجه الخصوص ، يتم استخدام هذا النهج لتحليل الإشارة باستخدام نافذة تحويل فورييه ، أو العكس في التوليف ؛ وكذلك في المعالجة الطيفية مثل إزالة الضوضاء وتغيير الإيقاع والتصفية غير الخطية وضغط البيانات الصوتية وغيرها.

يتم تمثيل عملية التقسيم نفسها رياضياً عن طريق الضرب بواسطة بعض وظيفة الوزن ( النافذة ) مع الإزاحة. بالنسبة إلى أبسط نافذة - مستطيلة - قد تبدو كما يلي:

إشارة المصدر:



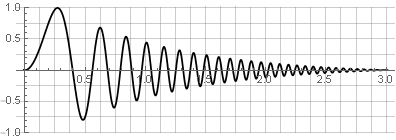
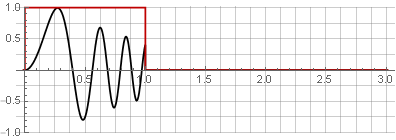
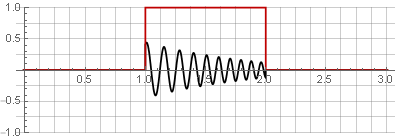
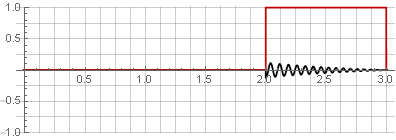
الأقسام:







يمكنك استعادة الإشارة الأصلية بمجرد إضافتها.

مزيد من التفاصيل

ولكن بواسطة لعدد من الأسباب ، ليست الوظيفة المستطيلة هي أفضل وظيفة للنافذة. في التحليل الطيفي ، من خلال تحويل فورييه المنفصل (السريع عادة) ، تبدو كتلة البيانات التي تم تحليلها "حلقة" ، مما يؤدي إلى فجوة في حواف وتشويه الطيف:



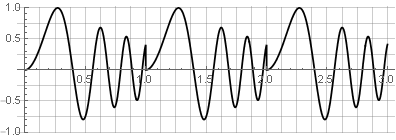
كما أنها غير مناسبة للتوليف العكسي - لأن أي تغيير سيؤدي أيضًا إلى حدوث فواصل - على سبيل المثال ، إذا حاولنا عكس أحد الأجزاء:



للقضاء على هذه العيوب ، يتم استخدام التداخل - عندما تلتقط كل نافذة لاحقة جزءًا من البيانات من النافذة السابقة ؛ ونافذة الوزن ، على التوالي ، تسقط تدريجياً إلى الحواف.

التداخل بنسبة 50٪

غالبًا ما يستخدمون نافذة Hannah (المعروفة أيضًا باسم "جيب التمام المرتفع") مع تداخل 50٪:








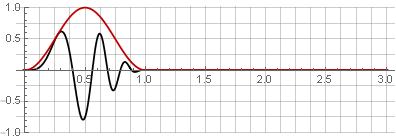
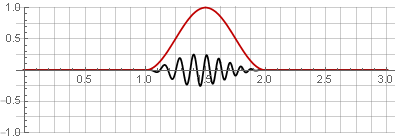
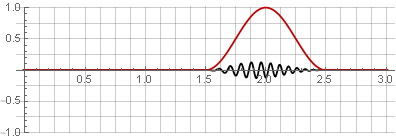
بسبب تناظر دالة جيب التمام أثناء الجمع ، يتم تلخيصها في الوحدة:



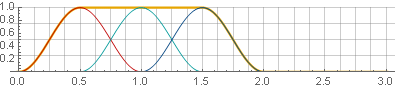
الآن ، مع التركيب العكسي ، لن نحصل على فجوات - ولكن بشرط أن تظل القيم عند حدود النافذة إلى الصفر. على سبيل المثال ، عند عكس أحد الأجزاء ، لن يتم انتهاك النعومة:

معالجة طبقة مزدوجة

ضع في اعتبارك بمزيد من التفاصيل خوارزمية معالجة الإشارة باستخدام تحويل فورييه السريع (FFT):

1. تقسيم الإشارة إلى أجزاء مع تراكب النافذة ؛
2. FFT المباشر ؛
3. معالجة الطيف ؛
4. عكس FFT.
5. تراكب النافذة المتكررة (لأنه بعد FFT العكسي ، لن يتم إرساء الحدود بالضرورة إلى الصفر دون كسر) ؛
6. تلخيص الأجزاء الناتجة.

علاوة على ذلك ، إذا لم تتم معالجة الطيف ، فينبغي أن تكون إشارة الخرج مطابقة لإشارة الدخل (فقط مع تأخير زمني لا مفر منه).

عند استخدام نافذة هان ، لم يعد التداخل بنسبة 50 ٪ كافيًا ، حيث ستحدث الانخفاضات:



نظرًا لأن التداخل المزدوج هو بمثابة تربيع ، فإن الحل الواضح هو استخدام جذر نافذة هان للتعويض عن التربيع:



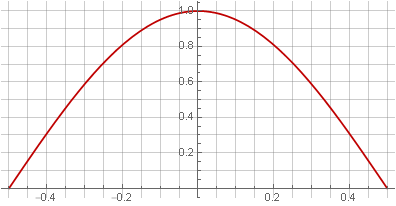
في هذه الحالة ، ومع ذلك ، توقفت النافذة لتكون سلسة عند الحواف - ظهرت فجوة في المشتق الأول.


يمكنك الذهاب في الاتجاه الآخر - استخدام التداخل بنسبة 75٪ ، وبعد ذلك سيتم أيضًا تلخيص النوافذ في ثابت - ليس فقط في $$$1$ و $$$\ frac {3} {2}$ :



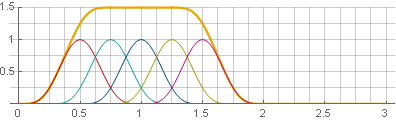
في هذه الحالة ، كنا محظوظين فقط. إذا قمنا بتوسيع المربع في المجموع ، فيمكننا أن نرى أنه يتكون من نافذتي هانا ، ولكن بمقاييس مختلفة ، مما يسمح لنا بتلبية المتطلبات التي نحتاجها:

$$

$$\ left (\ frac {\ cos (2 \ pi x) +1} {2} \ right) ^ 2 = \ frac {\ cos (2 \ pi x) +1} {2} + \ frac {\ cos (4 \ pi x) -1} {8}$$

مع وظائف النافذة الأخرى ، لن تعمل هذه الخدعة ؛ أيضا ، لا يمكن لجميع وظائف النافذة القياسية توفير الجمع في ثابت حتى عند تداخل 50 ٪.

فكرة

يمكننا أن نعتبر نافذة هان ليست وظيفة مستقلة ، ولكن كالفرق بين وظيفتين متواصلتين متتاليتين (تم تخصيص مقال منفصل لمناقشة تفصيلية لهم) مع تعويض. على سبيل المثال ، استخدام الوظيفة التالية

$$

$$\ left \ {\ start {array} {ll} -1 & x \ leqslant -1 \\ 1 & x \ geqslant 1 \\ \ sin \ left (\ frac {\ pi x} {2} \ right) و -1 <x <1 \\ \ end {array} \ right.$$

يمكن أن يكتب

$$

$$f (x + 1) -f (x-1)$$

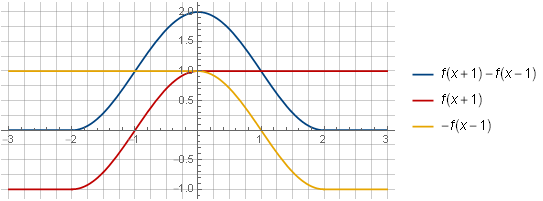
بعد النظر في مكونات مجموع نافذتين ، ستصبح قدرتهم على التلخيص في ثابت أكثر وضوحًا:



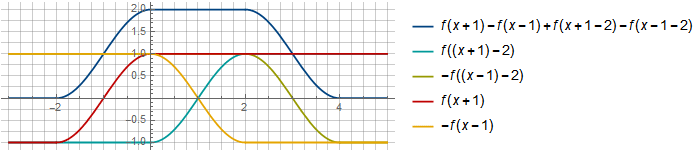
في الجزء $$$[0،2]$ تلقينا تعويضات متبادلة بالإضافة إلى الوظائف $$$-f (x-1)$ و $$$f ((x + 1) -2)$ منذ ذلك الحين $$$f ((x + 1) -2) = f (x-1)$

يمكنك اختيار إزاحة أخرى ، مع مزيد من التداخل ، على سبيل المثال:

$$

$$f \ left (x + \ frac {1} {2} \ right) -f \ left (x- \ frac {1} {2} \ right)$$

وبعد ذلك ، عند التحول في الخطوات $$$\ frac {1} {2}$ ، سيتم تلخيصها أيضًا في ثابت:



يمكن ملاحظة أنه إذا قمت بإعادة ترتيب مكونات وظيفة النافذة ، فستحصل على نفس نوافذ هان.

وبالتالي ، باستخدام وظائف تقييد مختلفة ، من الممكن تشكيل نوافذ بالشكل المطلوب.

الصيغة النهائية

الآن يبقى فقط لضبط المقياس بحيث لا تعتمد مناطق التعريف والقيم على مقدار التداخل. تحديد نافذة على فاصل زمني $$$[0،1]$ نحصل

$$

$$\ frac {f \ left (\ frac {2 tx} {t-1} -1 \ right) -f \ left (\ frac {2 t (x-1)} {t-1} +1 \ right) } {2}$$

اين $$$f$ - قم بتدريج الوظيفة المستمرة للنموذج

$$

$$\ left \ {\ start {array} {ll} -1 & x \ leqslant -1 \\ 1 & x \ geqslant 1 \\ g (x) & -1 <x <1 \\ \ end {array} \ حق.$$

لكن $$$g$ - بعض وظيفة الاستيفاء بين النقاط $$$(- 1، -1)$ و $$$(1،1)$ .

معلمة $$$t$ يحدد مستوى التداخل - فاصل يحدد الخطوة التي يجب من خلالها تغيير كل نافذة تالية ، $$$x_ {n + 1} = x_n + \ frac {1} {t}$ ، ويجب أن يكون أكبر من واحد ، $$$t> 1$ .

نسبة التداخل $$$p$ يمكن حسابها بالصيغة

$$

$$p = \ frac {100 (t-1)} {t}$$

والعكس صحيح

$$

$$t = \ frac {100} {100-p}$$

سيعتمد المظهر النهائي للنافذة على اختيار مستوى التداخل واختيار وظيفة التحديد.

بعض الأمثلة المثيرة للاهتمام

هنا سنلقي نظرة على بعض الحلول الجاهزة ، والتي بدأ كل شيء من أجلها. من أجل البساطة ، نعتبر وظيفة الاستيفاء ببساطة $$$g (x)$ ، بدون أي ربط آخر.

نوافذ كثيرة الحدود

هم الأقل تكلفة من الناحية الحسابية. باستخدام الصيغة المشتقة سابقًا

$$

$$\ frac {2 x \ Gamma \ left (n + \ frac {1} {2} \ right) \، _2F_1 \ left (\ frac {1} {2}، 1-n؛ \ frac {3} {2} ؛ x ^ 2 \ right)} {\ sqrt {\ pi} \ Gamma (n)}$$

نحصل على كثيرات الحدود مع عدد معين من الأصفار على مشتقات أعلى توفر السلاسة اللازمة للنافذة عند الحواف.


مع تداخل 75٪ من النافذة بقيم مختلفة من n ، ستبدو النوافذ على النحو التالي:



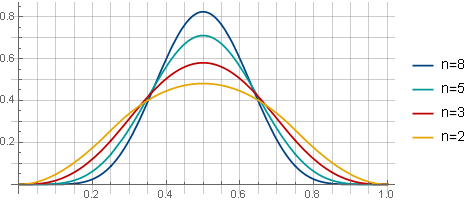
وفي حالة استخراج الجذر - مثل هذا (عند استخدام 75٪ من التداخل):



أو نحو ذلك (عند استخدام 50٪ من التداخل):

النافذة الأكثر سلاسة

الوظيفة

$$

$$\ tanh \ left (\ frac {k x} {\ sqrt {1-x ^ 2}} \ right)$$

من المثير للاهتمام أنه قابل للتمييز بشكل لا نهائي وجميع مشتقاته عند الحواف هي 0 (والتي يمكن إثباتها من خلال النظر في مشتقاتها على أساس قواعد التمايز - في كل مصطلح سيكون هناك عامل صفري). هذا يسمح لنا ببناء النوافذ على أساسها ، وجميع مشتقاتها ليس لديها فجوات:

نافذة عرض "تنورة"

تنجم الحاجة إلى هذا النوع من النوافذ عن طريق زيادة دقة FFT ، ولكن تقليل تأثير "عدم اليقين بشأن تردد الوقت" على الترددات العالية عن طريق زيادة تركيزها في المركز.

أولاً ، نحدد نوع وظيفة النافذة المطلوب - على سبيل المثال ، على النحو التالي:

$$

$$- \ تسجيل \ يسار (k ^ 2 x ^ 2 + 1 \ يمين) + \ تسجيل \ يسار (k ^ 2 + 1 \ يمين) - \ frac {k ^ 2 \ left (1-x ^ 2 \ right) } {k ^ 2 + 1}$$

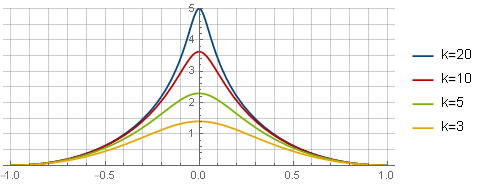
هنا ، المصطلح الأول يحدد شكل الوظيفة نفسها ، والثاني - يوفر التقاطع مع محور الخراج ، والثالث (القطع المكافئ) يعيد المشتق عند حواف الإرساء السلس ؛ والمعلمة $$$ك$ يعرف "حدة" الذروة. في هذا النموذج ، ليس مناسبًا للاستخدام بعد - تحتاج أولاً إلى الحصول على وظيفة التقييد منها من خلال التكامل والقياس:

$$

$$\ frac {kx \ left (k ^ 2 \ left (x ^ 2 + 3 \ right) +6 \ right) +3 \ left (k ^ 2 + 1 \ right) \ left (kx \ left (\ log \ اليسار (k ^ 2 + 1 \ right) - \ log \ left (k ^ 2 x ^ 2 + 1 \ right) \ right) -2 \ tan ^ {- 1} (kx) \ right)} {4 k ^ 3-6 \ يسار (k ^ 2 + 1 \ يمين) \ tan ^ {- 1} (k) +6 k}$$

للراحة ، يمكنك ربط المعلمة $$$ك$ إلى مستوى التداخل $$$t$ - على سبيل المثال ، بحيث تكون المشتقة الرابعة في وسط النافذة 0 - ثم $$$ك$ سيعتبر على النحو $$$\ sqrt {3} (t-1)$ :



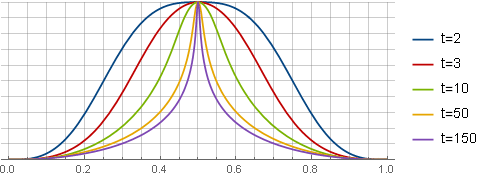
هنا ، من أجل الوضوح ، يتم تصغير جميع النوافذ بنفس المقياس.

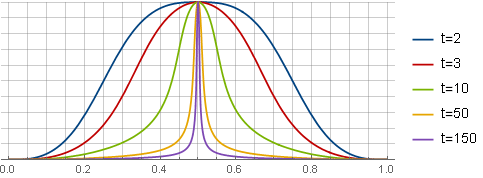
نافذة عرض الإبرة

إنها نسخة أكثر "عدوانية" من النافذة السابقة. تم اختيار المبالغة كأساس ، من خلال التحولات المتتالية

$$

$$\ frac {1} {x} \ to \ frac {1} {\ sqrt {x ^ 2}} \ to \ frac {1} {\ sqrt {x ^ 2 + 1}} \ to \ frac {1} {\ sqrt {k ^ 2 x ^ 2 + 1}} \ to \ frac {\ left (1-x ^ 2 \ right) ^ 2} {\ sqrt {k ^ 2 x ^ 2 + 1}}$$

وباستخدام نفس الخطوات في شكل التكامل والقياس حصلت على الصيغة

$$

$$\ frac {kx \ left (2 k ^ 2 \ left (x ^ 2-4 \ right) -3 \ right) \ sqrt {k ^ 2 x ^ 2 + 1} + \ left (8 \ left (k ^ 4 + k ^ 2 \ right) +3 \ right) \ sinh ^ {- 1} (kx)} {\ left (8 \ left (k ^ 4 + k ^ 2 \ right) +3 \ right) \ sinh ^ {-1} (k) -3 k \ sqrt {k ^ 2 + 1} \ left (2 k ^ 2 + 1 \ right)}$$

هنا يمكنك أيضًا ربط المعلمة $$$ك$ إلى مستوى التداخل. الحل المباشر لمعادلة المشتق الرابع يعطي نتيجة مرهقة ، لذا قم فقط بعمل الصورة للنافذة السابقة في الصورة والتشابه من خلال تحديد $$$ك$ كيف $$$k (t-1)$ وبالتالي ضمان دور المعلمة $$$ك$ باسم "الضبط الدقيق". في $$$k = 2.22$ ستبدو النوافذ على النحو التالي:

نافذة غير متماثلة

لا يجب أن تكون وظيفة النافذة متماثلة على الإطلاق. لنفترض أننا بحاجة إلى نافذة بها هجوم حاد وتوهين سلس. يمكننا الحصول عليها وفقًا لمخطط مألوف بالفعل - أولاً نحدد الشكل المطلوب للوظيفة ، ثم عن طريق التكامل نحصل على وظيفة التقييد. هنا تكون المهمة أكثر تعقيدًا بعض الشيء نظرًا لحقيقة أنه بسبب عدم التماثل ، لن يمر المركز من خلال الأصل ، لذلك تتم إضافة خطوة حسابية إضافية. هذا يؤدي أيضًا إلى حقيقة أن الصيغ نتيجة لذلك مرهقة إلى حد ما. على سبيل المثال ، ضع في اعتبارك الخيار الأبسط - القطع المكافئ مضروبًا في نافذة وزن متعدد الحدود:

$$

$$(1-x) ^ 2 \ left (1-x ^ {10} \ right) ^ 2$$

هنا ، تحدد درجة x في النافذة الموزونة (أي 10) "حدة" الهجوم. استخدمنا قيمة محددة ، بدلاً من معلمة رمزية ، لتبسيط صيغ الوضوح - إذا كنت ترغب في ذلك ، يمكنك إعادة حسابها لاحقًا.

بعد الدمج ، لم يعد القياس ببساطة كافيًا - ما زلت بحاجة إلى محاذاة الحواف:



للقيام بذلك ، نقوم أولاً بتحويل الوظيفة لأعلى لمحاذاة الحافة اليسرى ، ثم تحجيمها إلى اثنين على الحافة اليمنى وطرح واحد. ثم نحصل على الصيغة التالية:

$$

$$\ frac {8775 \ left (\ frac {x ^ {27}} {27} - \ frac {2 x ^ {26}} {26} + \ frac {x ^ {25}} {25} - \ frac {2 x ^ {15}} {15} + \ frac {4 x ^ {14}} {14} - \ frac {2 x ^ {13}} {13} + \ frac {x ^ 3} {3} -x ^ 2 + x + \ frac {117592} {61425} \ right)} {9856} -1$$

من أجل أن يكون للنافذة النهائية المظهر المطلوب ، من الضروري أيضًا توفير مستوى كبير بما يكفي من التداخل:

الخلاصة

وبالمثل ، يمكنك بناء النوافذ من أي وظائف أخرى على شكل جرس - على سبيل المثال ، Gaussians ؛ ويمكنك أيضًا تعديل تلك التي تم التفكير فيها بالفعل لتوفير نعومة أكبر أو تغيير شكل المنحنى.

وبصرف النظر ، بقيت التركيبة الطيفية لوظائف النافذة هذه - ينبغي تكريس دراسات منفصلة لهذا الغرض.

يمكن تنزيل نسخة أكثر تقدمًا قليلاً من المقالة (مع القدرة على تغيير المعلمات ديناميكيًا في النوافذ قيد النظر والصيغ المخفية) في شكل مستند Wolfram Mathematica هنا .