كم عدد المبرمجين الذين تحتاجهم لدعم التعليمات البرمجية المكتوبة مسبقًا؟

منذ بعض الوقت ، جرت محادثة بيني وبين صديقي العزيز ، حيث ظهرت العبارات التالية:

- سيزداد عدد المبرمجين باستمرار - لأن حجم الكود ينمو ، ويطلب المزيد والمزيد من المطورين باستمرار لدعمه.
- لكن الكود يتقدم في السن ، وجزء منه يترك الدعم. لا يستبعد وجود نوع من التوازن.

استدعاؤهم بعد بضعة أيام ، تساءلت عما إذا كان دعم التعليمات البرمجية ، الذي يتطلب المزيد والمزيد من الموارد بمرور الوقت ، يمكن أن يشل في نهاية المطاف تطوير وظائف جديدة ، أو يتطلب زيادة غير محدودة في عدد المبرمجين؟ ساعد التحليل الرياضي والمعادلات التفاضلية على التقييم النوعي لاعتماد حجم الدعم على التنمية والعثور على إجابات للأسئلة.

السؤال الأول. يمكن دعم "أكل" جميع موارد التنمية؟

فكر في فريق من المبرمجين يكون فيه عدد المشاركين ثابتًا. حصة وقت عملهم $$$\ mu (t)$ ( $$$0 <\ mu (t) <1$ ) التي تم حسابها من خلال تطوير رمز جديد ، والجزء المتبقي من الوقت $$$1- \ mu (t)$ يذهب إلى الدعم. بموجب افتراضات النموذج ، نفترض أن النوع الأول من النشاط يهدف إلى زيادة كمية التعليمات البرمجية ، والثاني - تغييره (تصحيح الأخطاء) ولا يؤثر بشكل كبير على كمية التعليمات البرمجية.

نشير $$$y (t)$ كل رمز مكتوب بالوقت $$$t$ . النظر في سرعة كتابة التعليمات البرمجية بشكل متناسب $$$\ mu (t)$ نحصل على:

$$

$$\ frac {dy (t)} {dt} = a_0 \ mu (t) ؛ a_0 \ in \ mathbb {R}، a_0> 0.$$

من الطبيعي أن نفترض أن العمل الذي ينطوي عليه الحفاظ على الكود يتناسب مع حجمه:

$$

$$1- \ mu (t) = a_1 y (t) ؛ a_1 \ in \ mathbb {R} ، a_1> 0$$

أو

$$

$$\ mu (t) = 1-a_1y (t)$$

من أين

$$

$$\ frac {dy (t)} {dt} = a_0 (1-a_1y (t))).$$

نحصل على معادلة تفاضلية تتكامل بسهولة. إذا كان مقدار الرمز صفرًا في اللحظة الأولى ، فعندئذٍ

$$

$$y (t) = \ frac {1} {a_1} (1-e ^ {- a_0a_1t}).$$

في $$$t \ to + \ infty$ الوظيفة $$$y (t) \ to1 / a_1$ و $$$\ mu (t) \ إلى 0$ . وهذا يعني انخفاضًا تدريجيًا بمرور الوقت في تطوير وظائف جديدة إلى الصفر وانتقال جميع الموارد إلى الدعم.

ومع ذلك ، إذا كان في الوقت المناسب $$$h> 0$ نظرًا لأن الرمز أصبح قديمًا ويتوقف دعمه ، فإن حجم الرمز الذي يتطلب الدعم في كل مرة $$$t$ يساوي $$$y (t) - y (t-h).$ ثم

$$

$$1- \ mu (t) = a_1 (y (t) - y (t-h)) ،$$

$$

$$\ mu (t) = 1-a_1 (y (t) - y (t-h)) ،$$

لكن $$$y (t)$ هو حل معادلة تفاضلية بحجة متأخرة [1]:

$$

$$\ frac {dy (t)} {dt} = a_0 (1-a_1 (y (t) - y (t-h))).$$

يتم تحديد حل هذه المعادلة بشكل فريد من خلال تحديد القيم $$$y (t)$ "قبل بداية الوقت" مع $$$t \ in [-h، 0]$ . نظرًا لعدم كتابة أي رمز قبل الوقت الأولي ، في حالتنا $$$y (t) = 0$ في $$$t \ in [-h، 0]$ .

دعونا نلقي نظرة على بعض الأمثلة. سنقيس الوقت بالسنوات ومقدار الشفرة بآلاف الأسطر. ثم ل $$$a_0$ قيم ترتيب العشرات مقبولة ، نأخذ 50 و 100. أي أنه في السنة سيكتب فريق التطوير خمسين ومائة ألف سطر من التعليمات البرمجية ، على التوالي. ل $$$a_1$ قد تكون القيم المقبولة: $$ ، $$ ، $$$1 / a_0$ . وهذا يعني أن فريق التطوير قادر على الحفاظ على مقدار الرمز الذي كتبه للعام ، بربع أو نصف أو عبء عمل كامل. كمتوسط ​​عمر التعليمات البرمجية ، فلنقم بتعيين القيم: 1 و 2 و 4 سنوات. حل المعادلة عدديًا ، نحصل على أمثلة لسلوك الدالة $$$\ mu (t)$ لبعض تركيبات المعلمات $$$h ، a_0 ، a_1$ .

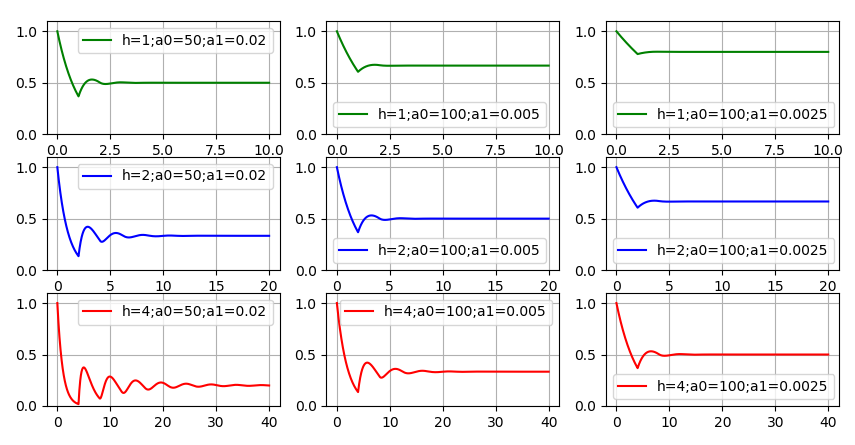
سلوك الوظيفة $$$\ mu (t)$ في مواجهة رمز الشيخوخة. الوظيفة لم تعد رتيبة ، لكن التقلبات "تهدأ" بمرور الوقت ، هناك ميل نحو $$$\ mu (t)$ إلى بعض القيمة الثابتة. تظهر الرسوم البيانية: أكثر $$$h$ ، $$$a_0$ و $$$a_1$ ، أي أنه كلما كان الرمز أبطأ ، كلما كان تطور الرمز الجديد أسرع وكلما انخفضت جودة الرمز ، كلما قلت الموارد لتطوير وظائف جديدة. كانت هناك رغبة في إعطاء مثال واحد على الأقل $$$\ mu (t)$ "تكبب" قريبة من الصفر. ولكن هذا يتطلب اختيار مؤشرات جودة التطوير رديئة للغاية وكود طويل العمر. حتى في الرسم البياني السفلي الأيسر ، لا يزال هناك قدر كبير من الموارد للوظيفة الجديدة. لذلك ، فإن الإجابة الصحيحة على السؤال الأول هي على الأرجح: من الناحية النظرية - نعم ، هذا ممكن ؛ عمليا - بالكاد.

أسئلة لا يمكن الإجابة عليها:

1. هل هذا صحيح $$$\ mu (t)$ يميل إلى حد معين ل $$$t \ to + \ infty$ للجميع $$$a_0 ، a_1> 0$ ؟؟؟ إن لم يكن للجميع ، فمن أجل ماذا؟
2. إذا كان الحد موجودًا ، فكيف تعتمد قيمته على $$$a_0 ، a_1$ ؟؟؟

السؤال الثاني. هل يمكن أن يؤدي دعم التعليمات البرمجية إلى نمو غير محدود في عدد المبرمجين؟

نشير $$$q (t)$ عدد المبرمجين المشاركين في تطوير الكود الجديد. كما ورد أعلاه $$$y (t)$ - مقدار الرمز المكتوب في الوقت $$$t$ . ثم

$$

$$\ frac {dy (t)} {dt} = a_2 q (t) ؛ a_2 \ in \ mathbb {R}، a_2> 0.$$

دع التعليمات البرمجية مشغولة $$$p (t)$ المبرمجين. الشيخوخة رمز C

$$

$$p (t) = a_3 (y (t) -y (t-h)) ؛ a_3 \ in \ mathbb {R}، a_3> 0.$$

من أين

$$

$$p (t) = a_3 \ int_ {t-h} ^ {t} \ frac {dy (s)} {ds} ds = a_2a_3 \ int_ {t-h} ^ tq (s) ds.$$

إذا $$$q (t) \ leq C_1$ ثم

$$

$$p (t) \ leq a_1a_2C_1h.$$

وبالتالي ، فإن الإجابة على السؤال الثاني هي سلبية: إذا كان عدد مطوري الكود الجديد محدودًا ، ففي سياق الكود القديم ، لا يمكن للدعم أن يسبب زيادة غير محدودة في عدد المبرمجين.

الخلاصة

النماذج المدروسة هي نماذج رياضية "لينة" [2]. إنها بسيطة للغاية. ومع ذلك ، فإن اعتماد نتائج المحاكاة على قيم المعلمات يتوافق مع تلك المتوقعة للأنظمة الحقيقية ؛ وهذا يتحدث لصالح كفاية النماذج والدقة الكافية للحصول على تقديرات نوعية.

المراجع

1. Elsgolts L.E.، Norkin S.B. مقدمة في نظرية المعادلات التفاضلية بحجة الانحراف. موسكو دار النشر "علوم". 1971.
2. Arnold V.I. النماذج الرياضية "الصلبة" و "اللينة". موسكو دار النشر للمركز. 2004